прилож.2. Рабочий лист урока (1)

Алгебра: раздел 1.

График функции и преобразования.

Существует 4 способа преобразования графика функции. Исходная функция f (x) часто называется родительской функцией и имеет конкретные свойства и ключевые моменты, помогающие в построениях.

1)      Вертикальный сдвиг: График смещается _____________________________________________

2)      Горизонтальный сдвиг: График смещается____________________________________________

3)      Сжатие/растяжение в вертикальном направлении: ___________________________________

4)      Сжатие/растяжение в горизонтальном направлении: _________________________________

Определите точки данного исходного графика фукции f(x):

·        

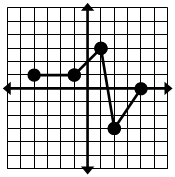
-1•f(x)   2•f(x)   f(x – 2)   ½•f(x)

Определите точки исходной фукции g(x) из графика:

·        

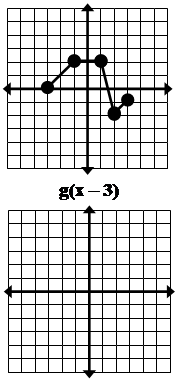
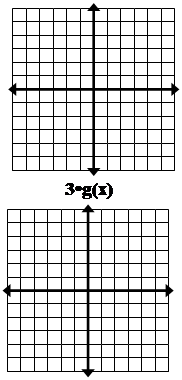
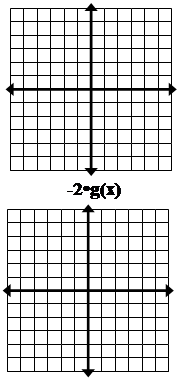
Как различные операции над исходной функцией создают преобразования?

1)      Вертикальный сдвиг:

a.      вверх:   

b.      вниз:  

2)      горизонтальный сдвиг:

a.      влево:

b.      вправо:  

3)      сжатие/растяжение в вертикальном направлении:

a.      растяжение:   

b.      сжатие:  

c.       переворот:   

ОБЩАЯ ФОРМА ДЛЯ ПРЕОБРАЗОВАНИЙ ФУНКЦИИ f(x): a • f(x – h) + k

ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ ДЛЯ ДАННЫХ ВЫРАЖЕНИЙ

Для исходных функций f(x), g(x), или h(x)

1)         f(x – 1) + 2

2)         h(x + 7) + 8

3)         2f(x – 1)

4)         -3 f(x) + 2

5)         ½ g(x) – 9

6)         -³/₄h(x + 6)

7)         2f(x + 3) – 5

8)         –g(x – 4) + 7

9)         ²/₃h(x + 1) + 5

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ И ИХ ПРЕОБРАЗОВАНИЯ

АБСОЛЮТНАЯ ВЕЛИЧИНА:

·       

·        Важная точка: (h, k)
  

·        Область определения:

·        Область значения:

·        Исходная функция: f(x) = x²

·        Ключевая точка: (h, k)
  

·        Область определения:  

·        Область значений:  

Практика построения преобразований функций

Раздел  1. График преобразования

1)     

2)     

3)     

4)                                     

5)     

6)     

7)     

Квадратный корень:

·       Исходная функция: 

·       Важная точка: (h, k)

·       Область определения:

·       Область значений:  

Кубическая функция:

Исходная функция: f(x) = x³

·       Ключевая точка:  (h, k)

·       Область определения:  

·        Область значений:  

Практика построения преобразований графиков

Раздел 1. Графики

1)     

2)     

3)     

4)     

5)     

6)     

7)     

8)     

9)     

10)