Приложение 3.Методы решения задач docx

Приложение 3

Широко распространены задачи, в условиях которых говорится о двух прогрессиях: арифметической и геометрической. Как правило, для решения таких задач достаточно учесть характеристические свойства этих прогрессий.

 Работа в группах. На ИД показывается задание. Учащихся объединить в уровневые группы и попросить учащихся решить самостоятельно задачу. Если учащиеся могут решить самостоятельно, то им можно показать остальные два способа.

Цель данной групповой работы:

Рассмотреть одну задачу и все три способа решения чтобы определить какие характеристические свойства должны учесть при решении задач.

Первая группа.

Три числа образуют арифметическую прогрессию. Если к первому числу прибавить 8, получится геометрическая прогрессия с суммой членов 26. Найти эти числа.

Первый способ:

Пусть эти числа а, b, с. Так как они образуют арифметическую прогрессию, то выполнено соотношение (свойство арифметической прогрессии): 2b = а + с.

После сложения первого числа с числом 8 получаем числа (а + 8), b, с, которые образуют геометрическую прогрессию. Запишем ее свойство: b² = (а + 8)с.

Кроме того, известно, что сумма членов геометрической прогрессии равна 26, т. е. (а + 8) + b + с = 26. Получаем для определения а, b, с систему уравнений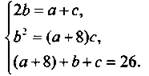

Запишем третье уравнение системы в виде (а + с) + b = 18. Учитывая первое уравнение системы, получим: b + 2b= 18, b = 6.

Тогда из первого и второго уравнений получаем систему для определения а и с: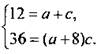

Выразив из первого уравнения с = 12 - а и подставив во второе, получим уравнение 36 = (а + 8) · (12 - а), или а² - 4а - 60 = 0. Корни этого уравнения а = -6 и а = 10. Соответствующие им числа: с = 18 и с = 12.

Таким образом, искомые числа: -6, 6, 18 и 10, 6, 2.

Рассмотрим еще два способа решения этой задачи, которые позволяют уменьшить число неизвестных и сразу учесть свойство той или иной прогрессии.

Вторая группа

Три числа образуют арифметическую прогрессию. Если к первому числу прибавить 8, получится геометрическая прогрессия с суммой членов 26. Найти эти числа.

Второй способ:

Так как числа а, b, с образуют арифметическую прогрессию, го можно записать: b = a + d, c = a + 2d (где d - разность этой прогрессии). При этом учтено свойство арифметической прогрессии 2b = а + с (действительно,

2(а + d) = а + (а + 2d)). После прибавления к первому числу числа 8 получаем числа (а + 8), (а + d), (а + 2d). Сумма этих чисел равна 26, т. е. (а + 8) + (а + d) + (а + 2d).

Имеем систему уравнений для определения a, d: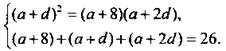 

Из второго уравнения а + d = 6, откуда d = 6 - а.

Тогда из первого уравнения имеем: 36 = (а + 8)(12 - а),

а² - 4а - 60 = 0. Решив это уравнение, найдем: а = -6 и а = 10.

Тогда соответствующие значения d: d = 12 и d = -4.

После этого находим числа: а = -6, b = 6, с = 18 и а = 10, b = 6, с = 2.

И наконец, третий способ решения позволяет учесть свойства геометрической прогрессии.

Третья группа

Три числа образуют арифметическую прогрессию. Если к первому числу прибавить 8, получится геометрическая прогрессия с суммой членов 26. Найти эти числа.

Третий способ

Так как числа (a + 8), b, с образуют геометрическую прогрессию, то можно записать: b= (a + 8)q, с = (а + 8)q². При этом выполнено свойство геометрической прогрессии 

b² = (а + 8) с (действительно,

[(a + 8)q]² = (а + 8)[(а + 8)q²]).

Сумма этих чисел:

(a + 8) + (a + 8)q + (a + 8)q² = (а + 8)(1 + q + q²) = 26. Числа а, b, с образуют арифметическую прогрессию, и можно записать ее свойство: 2(а + 8)q = а + (а + 8)q².

Прибавив к обеим частям уравнения 8 и перенеся слагаемое 2(а + 8)q из левой части в правую, получим: 8 = (а + 8) - 2(a + 8)q + (a + S)q2, или 8 = (a + 8)(1 - 2q + q²).

Для нахождения a и d имеем систему уравнений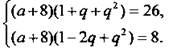 

Разделив уравнения друг на друга, получим:  или 3q² - 10q + 3 = 0, откуда 

q = 1/3, q = 3. Тогда, соответственно, находим из любого уравнения системы: а = 10 и а = -6.

Далее определяем b и с: 

b = 6, с = 2 и b = 6, с = 18.

Источник:

https://compendium.su/mathematics/algebra9/41.html

Скачано с www.znanio.ru