ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ. Самостоятельная работа 10 класс

Вариант№1

1.     На рисунке изображен график производной функции у= f(х). Укажите количество точек, в которых касательная к графику функции у= f(х) параллельна оси ОХ.

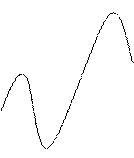                                                            у

                                                                                 У=f ^' (х)

                                                                                                                               х

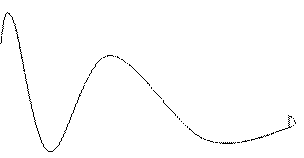
2.     На рисунке изображен график производной функции у= f(х). Укажите количество точек минимума функции и количество промежутков убывания.

                                                           У    

                                                                                                     У=f ^' (х)

                                                                                                                                 х

3.     Определите точки максимума функции у= х⁶ -48х² +2.

               4.Найти наименьшее целое число из промежутка убывания

                    функции у= х³ + 9х² -48х+1.

Вариант№2

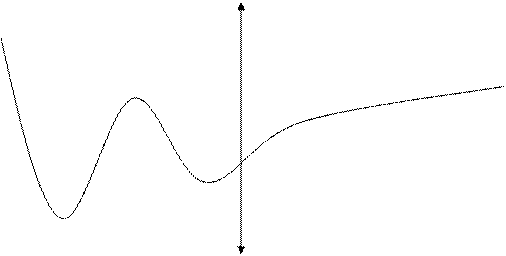
1.На рисунке изображен график производной функции у= f(х). Укажите количество точек, в которых касательная к графику функции у= f(х) параллельна  прямой у= -х

                                                         у

                                                                                 У=f ^' (х)

                                                                                                                     х

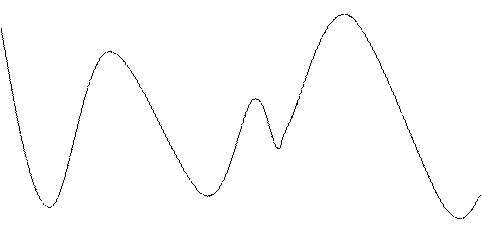
2.На рисунке изображен график производной функции у= f(х). Укажите количество точек максимума функции и количество промежутков возрастания.

                                                        у

                                                                                                 У=f ^' (х)

                                                                                                                  х

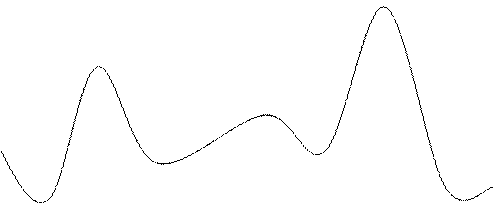
3.Определите точки максимума функции у=3 х⁴ – х¹² + 5.

4. Найти наибольшее целое число из промежутка убывания

        функции у= х³ + 12х² +14х -30.

Вариант№3

1. 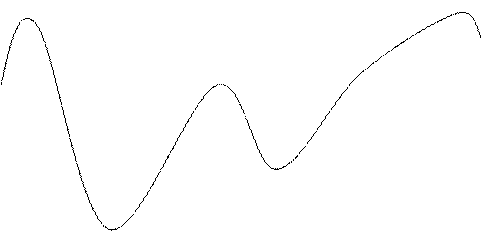    На рисунке изображен график производной функции у= f(х). Укажите количество точек, в которых касательная к графику функции у= f(х) составляет угол 45º с осью ОХ.

                                                      у

                                                                                                         У=f ^' (х)

                                                                                                                х

2. 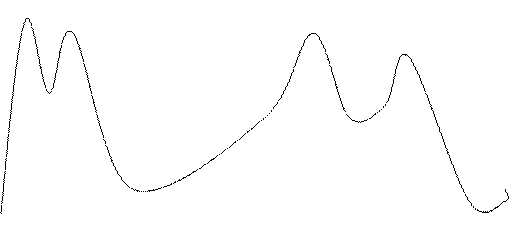    На рисунке изображен график производной функции у= f(х). Укажите количество точек максимума функции и количество промежутков убывания.

                                                          у

                                                                                                        У=f ^' (х)   

                                                                                                                         х

3.     Определите точки максимума функции у= 2х⁶ -12х³ +21.

                  4. Найти наименьшее целое число из промежутка возрастания

                         функции у= - х³ - 21х² - 63х + 225.

Вариант№4

1.На рисунке изображен график производной функции у= f(х). Укажите количество точек, в которых касательная к графику функции у= f(х) параллельна  прямой у= 1,5х

                                                            у

                                                                                                      У=f ^' (х)

                                                                                                                     х

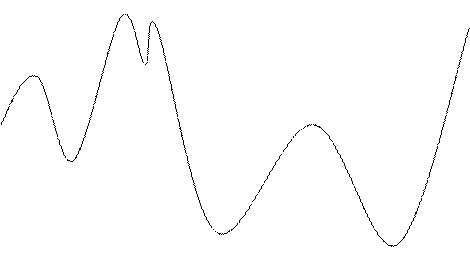
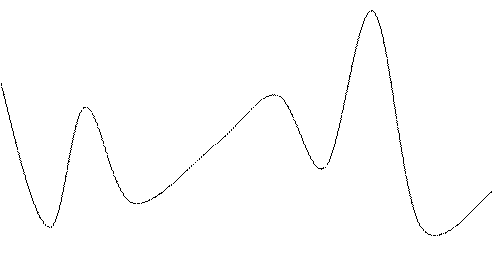2.На рисунке изображен график производной функции у= f(х). Укажите количество точек минимума функции и количество промежутков убывания.

                                                        у

                                                                                                         У=f ^' (х)

                                                                                                                     х

3.Определите точки максимума функции у=6 х³ – х² + 15.

4.     Найти наибольшее целое число из промежутка убывания

       функции у= -2х³ - 15х² +48х + 38