Задачи оптимизации в Excel
Пример решения производственной задачи
ЗАДАНИЕ.
Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
|
Вид сырья |
Нормы расхода сырья (кг) на одно изделие |
Общее количество сырья (кг) |
|
|
А |
В |
||
|
І |
12 |
4 |
300 |
|
ІІ |
4 |
4 |
120 |
|
ІІІ |
3 |
12 |
252 |
|
Прибыль от реализации изделия одного вида (руб.) |
30 |
40 |
|
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?
РЕШЕНИЕ.
Пусть предприятие производит ед. изделия А и ед. изделия В. Тогда
общая прибыль предприятия (целевая функция) составит: = 30 + 40 .
Требуется найти максимальное значение целевой функции при следующих
ограничениях:
|
3 |
124+ 12+ 4+ 4 ≤ 252≤ 120≤ 300 по ресурсу I
по ресурсу II
по ресурсу III
При этом полагаем, что искомые значения и могут быть неотрицательными. Получаем задачу линейного программирования:
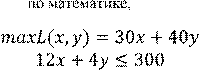экономике
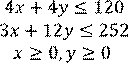
Для использования EXCEL заполняем страницу в соответствии с математической постановкой двойственной задачи:
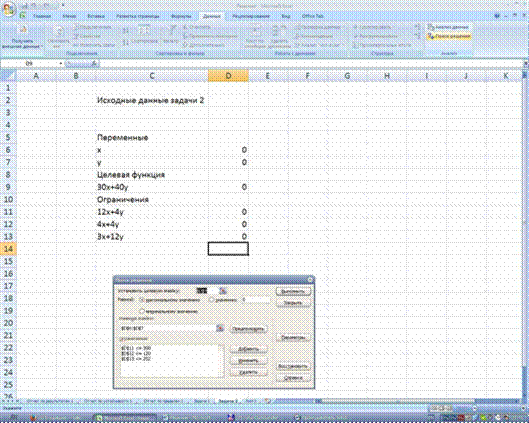
Для решения задачи ЛП в Excel используют во вкладке Анализ данных надстройку Поиск решения.
Целевая ячейка (Максимум)
|
Ячейка |
Имя |
Исходное значение |
Результат |
|
$D$9 |
30x+40y |
750 |
1080 |
Изменяемые ячейки
|
Ячейка |
Имя |
Исходное значение |
Результат |
|
$D$6 |
x |
25 |
12 |
|
$D$7 |
y |
0 |
18 |
Ограничения
|
Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
|
$D$11 |
12x+4y |
216 |
$D$11<=300 |
не связан. |
84 |
|
$D$12 |
4x+4y |
120 |
$D$12<=120 |
связанное |
|
|
$D$13 |
3x+12y |
252 |
$D$13<=252 |
связанное |
|
Таким образом, максимальная прибыль составито = 12 (о = 18, ) = 1080
руб.; значения оптимального плана производства: ед.; ед.
Решение двойственной задачи 2 с использованием пакета Excel
Степень дефицитности каждого вида ресурса оценим по двойственным
оценкам , , , найденнымmin (12) из= 300+ 4 решения+ 4, … ,+ 12+ 3+ 120 ≥ 0двойственной≥ 30≥ 40+ 252 задачи: 4
Для использования EXCEL заполняем страницу в соответствии с математической постановкой двойственной задачи:
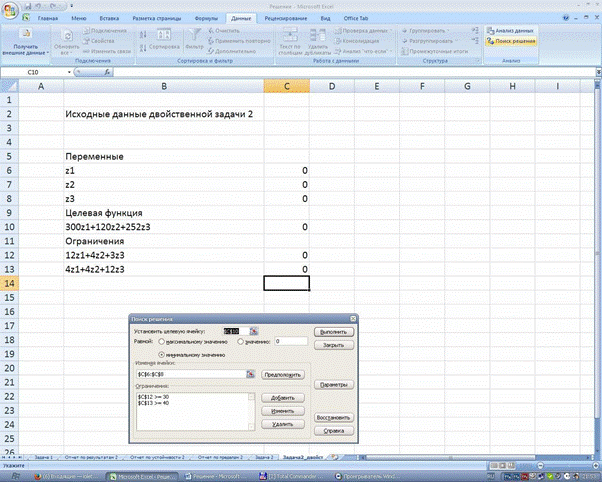
Для решения задачи ЛП в Excel используют во вкладке Анализ данных надстройку Поиск решения.
Целевая ячейка (Минимум)
|
Ячейка |
Имя |
Исходное значение |
Результат |
|
$C$10 |
300z1+120z2+252z3 |
0 |
1080 |
Изменяемые ячейки
|
Ячейка |
|
Имя |
Исходное значение |
|
Результат |
|
$C$6 |
z1 |
|
|
0 |
|
|
$C$7 |
z2 |
|
|
0 |
|
|
$C$8 |
z3 |
|
|
0 |
1,111111111 |
Ограничения
Ячейка Имя
Значение Формула Статус Разница
$C$12 12z1+4z2+3z3 30
$C$12>=30 связанное
$C$13 4z1+4z2+12z3 40 $C$13>=40 связанное
плана1080 исходной задачи составят = 0, = 6,67, = 1,11, min ( ) = Из решения задачи следует, что двойственные оценки оптимального
.
 |
Это означает, что первый вид ресурса не является дефицитным, и увеличение его запаса не принесет увеличение целевой функции. Напротив, второй и третий виды ресурсов являются дефицитными. Увеличение (уменьшение) запаса второго ресурса на одну единицу приведет к увеличению (или к уменьшению) прибыли на 6,67 руб. Увеличение (уменьшение) запаса третьего ресурса на одну единицу приведет к увеличению (или к уменьшению) прибыли на 1,11 руб.
Задачи оптимизации в Excel
I по ресурсу II по ресурсу
Ячейка Имя Исходное значение
Для использования EXCEL заполняем страницу в соответствии с математической постановкой двойственной задачи:
Для решения задачи ЛП в Excel используют во вкладке
C$12 12z1+4z2+3z3 30 $C$12>=30 связанное $C$13 4z1+4z2+12z3 40 $C$13>=40 связанное плана 1080 исходной задачи составят = 0 , = 6,67 , = 1,11 , min…
© ООО «Знанио»
С вами с 2009 года.
