Примеры построения и преобразования переключательных функций

 Примеры построения и преобразования переключательных функций

Пример 1. Дана таблица истинности, определяющая функции однораз- рядного сумматора. В суммировании участвуют одноразрядные двоичные числа a и b и входной перенос p. Результатом работы сумматора являет- ся арифметическая сумма s и перенос в следующий разряд. p_s. Получить аналитическую запись функций сумматора и его схему.

S = abp + ab p + ab p + abp = (ab p + ab p) + (abp + abp) = (ab + ab) p + (ab + ab) p =

= (a Å b) p + (aa + ba + ab + bb)p = (a Å b) p + (0 + ba + ab + 0)p = (a Å b) p + (a Å b)p = a Å b Å p

ps = abp + abp + ab p + abp

ps = (abp + abp) + (abp + abp) + (ab p + abp) = bp(a + a) + ap(b + b) + ab( p + p) =

= bp ·1 + ap ·1 + ab ·1 = bp + ap + ab = bp + ap + ab = bp · ap · ab

Используя условные графические обозначения для основных переклю- чательных функций, изобразим схему одноразрядного сумматора.

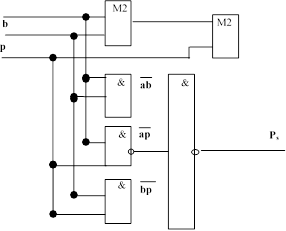a

Соединив последовательно по линии распространения пере- носа N таких схем, можно по- лучить сумматор для арифме- тического сложения N-раз- рядных двоичных чисел.

Y = x1 x2 x3 + x1 x2 x3 + x1 x2 x3 + x1 x2 (x3 + x1 x2 x3 ) = x1 x2 x3 + x1 x3 (x2 + x2 ) + x1 x2 x3 (1 + x1 x2 ) =

= x1 x2 x3 + x1 x3 ·1 = x1 x2 x3 + x1 x3 = x1 (x3 + x2 x3 ) = x1 (x3 + x2 x3 ) = x1 · (x3 · x2 · x3 )