Примеры проблемных ситуаций на уроках математики

Примеры  проблемных  ситуаций, используемых  мною на уроках  математики.

1.     Создание проблемных ситуаций через решение задач, связанных с жизнью.

Пример №1.      Тема «Периметр прямоугольника» ( 5 класс)

Семья Коли летом переехала в новый дом. Им отвели земельный участок прямоугольной  формы. Папа решил поставить изгородь. Он попросил Колю сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный метр изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей.

Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника).

 

          Пример №2. Тема «Нахождение дроби от числа» (6 класс)

1)                Решим задачу: «Огород занимает 6 га земляного участка. На 2/3 огорода посажен картофель. Какую часть всего земляного участка занимает картофель?» Можем ли мы решить задачу? Как?

(6/3*2 = 4 (га))

2)                Охарактеризуйте задачу. Отойдем от огорода и картофеля, перейдем к величинам. Что нам известно? [целое]. Что нужно найти? [часть]

3)                Возьмем ту же задачу, но изменим значения одной величины: «Огород занимает 4/5 земельного участка. На 2/3 огорода посажен картофель. Какую часть всего земельного участка занимает картофель?» Изменился ли математический смысл задачи? [нет]. Значит, опять известно целое, а ищем часть. Влияет ли замена 6 на 4/5 на решение? Можно ли решить?  [нет].

4)                Что за ситуацию мы получили?

[Обе задачи на нахождение части от числа. Но одну мы можем решить зная определенные дроби, понятие числителя и знаменателя, а вторую не можем].

Проблема: не знаем общего правила нахождения дроби от числа. Нужно вывести это правило.

 

 Пример №3  Тема “Площадь треугольника” (геометрия 8 класс)

Задача: «Три маляра должны покрасить фронтон дома в форме прямоугольного треугольника со сторонами 3м и 4 м. Хватит ли им 1 банки краски, если на ней написано: площадь покрытия  10г/кв.м.?»   

 Переведем задачу на математический язык:

      «Найдите площадь S прямоугольного треугольника, если один из катетов 3 м, а другой – 4 м» Отдельные ученики догадались -  зная формулу площади прямоугольника, смогут решить эту задачу.

Первая проблемная ситуация.

       «Как вычислить площадь прямоугольного треугольника, зная формулу для нахождения площади прямоугольника?»

       Дети предлагают: достроить данный треугольник до прямоугольника.(если прямоугольный треугольник достроим до прямоугольника, то мы получим два равных треугольника, которые равны по двум катетам)

     Вычисляют  площадь прямоугольника, а затем находят  площадь прямоугольного треугольника.

Вторая проблемная ситуация:  всегда ли можем использовать получившуюся формулу , если треугольники бывают разной формы?

Задача:  «Найти площадь любого остроугольного треугольника.»

       При помощи наводящих вопросов ученики находят способ. Они предлагают достроить остроугольный треугольник до параллелограмма.

•         Доказываем, что полученные 2 треугольника равны по 3-му признаку равенства треугольников.

•         Вспоминаем формулу площади параллелограмма;

•         Выводим формулу площади любого остроугольного треугольника ;

•         Отвечаем на вопрос задачи: площадь любого остроугольного треугольника равна половине произведения его основания на высоту.

Третья  проблемная ситуация:   «Найти площадь любого тупоугольного треугольника».

С этой проблемой ученики  справляются быстро.

Решаем основную проблему: «Найти площадь произвольного  треугольника”. Проанализировав  все случаи,  сделайте вывод.

 Вопрос: «Чему равна площадь произвольного треугольника?»

 Предполагаемый ответ учеников: «Площадь произвольного треугольника равна половине произведения его основания на высоту.»

Пример №4.  Тема: «Площадь прямоугольника» ( 5 класс)

На прошлом уроке ребята мы измеряли длину и ширину нашего класса и по формуле, нашли его периметр. Р==   (6+9)·2=30м. Помните!

Посмотрите, пожалуйста, на пол. Линолеум износился, много чёрных полос. Вам нравится? Мне тоже не нравится. Я думаю, что летом нам нужно обязательно постелить новый линолеум. Давайте с вами посчитаем,  сколько денег нужно будет собрать с каждого родителя на замену линолеума, если 1 погонный метр стоит 800 рублей. Проблемная ситуация.  Для решения этой задачи нам нужно найти площадь пола (площадь прямоугольника).

 

 

 

10 класс тема «Возрастание и убывание функций». До объявления темы урока предложить учащимся решение двух уравнений:

х³ = 27                                                                     х² = 9

х³ =3³                                                                       х² = 3²

х = 3                                                                        х = 3

 

            Уравнения решены одним и тем же способом и относятся к одному классу. Верно ли решены уравнении? (Второе уравнение решено неверно, кроме корня 3 имеет еще корень х = -3). У учащихся возникает вопрос почему? Решая эти уравнения мы выяснили при каких значениях аргумента х функция х³ принимает значение 27, а функция х² – значение 9? Результаты получились различные. В чем же дело? Очевидно дело в функциях х³ и х². Вероятно, что между функциями и х², которые относятся к одному классу функций существует весьма существенное различие? Для его отыскания ученикам предлагается начертить схематически графики функций и выяснить сколько раз функция х³ может принимать значение равное 27, а х² – значение 9? После этого ученики легко видят, что каждое свое значение х³ принимает только один раз, что нельзя сказать о функции х². Вспоминают как называются такие функции. Затем сообщается тема урока и идет работа над определениями возрастающей и убывающей функций.

2.     Создание проблемных ситуаций через выполнение практических заданий.

 

Пример №1. Тема «Площадь прямоугольника» .(5 класс)

На уроке технологии Дима выпиливал лобзиком и получил различные остатки фанеры. В каком из остатков выбрасывается фанеры больше?

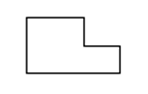
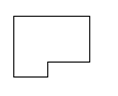
Проблемная ситуация. Нужно найти площадь данной фигуры.

Вывод: разбить фигуру на прямоугольники, найти площадь каждой части и сложить (один из вариантов)

  

Пример №3.  Тема «Координатная плоскость» (6 класс)

    На этапе активного и осознанного усвоения нового материала, а также на этапе закрепления применяю практические  работы «Животные на плоскости», «Астрономия и координатная плоскость». Ребята строят точки по координатам и рисуют животных и созвездия, затем рассказывают про них. Также выполняют  творческие работы, сами предлагают свои рисунки и по ним составляют задания.

 

Пример № 4. Темы: «Построение треугольника по трем элементам»,

                                   «Неравенство треугольника».(7 класс)
   Теорему о неравенстве треугольника вводим при изучении темы «Построение треугольника по трем элементам», решая задачу на построение треугольника по трем его сторонам. Предлагаем ученикам построить с помощью циркуля и линейки треугольник со сторонами: а) 5см; 6см; 7см;      б) 9см; 5см; 6см;  в) 1см; 2см; 3см;       г) 3см; 4см; 10см.
   Ребята работают самостоятельно и приходят к тому, что построить треугольник в последних двух примерах не удается. Возникает проблема: «При каких же условиях существует треугольник»? Чертежи, полученные учащимися при решении этой задачи,  дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон». Доказываем полученную теорему.

3.     Создание  проблемных ситуаций через решение задач на внимание и сравнение

Пример №5 Тема  «Сумма углов треугольника» (7 класс):

1) Построить треугольник по трем заданным углам:

•         ∟А=90°, ∟B=60°, ∟С=45°;

•         ∟А=70°, ∟B=30°, ∟С=50°;

•         ∟А=50°, ∟B=60°, ∟С=70°.

2) Два угла треугольника равны 118º и 62º. Найти величину третьего угла.

Пример №6. Тема: «Площадь трапеции». (8 класс)
     При выводе формулы для вычисления площади трапеции учитель предлагает учащимся воспользоваться ранее изученными формулами для вычисления площади прямоугольника, параллелограмма, треугольника, свойствами площадей.
     Ребята предлагают различные способы:
а) провести диагональ и найти площадь трапеции как сумму площадей двух треугольников;
б) провести две высоты и найти площадь трапеции как сумму площадей прямоугольника и двух прямоугольных треугольников;
в) провести прямую, параллельную боковой стороне трапеции и найти площадь трапеции как сумму площадей параллелограмма и треугольника.

 Пример №3.  Тема: «Четырехугольники». (8 класс)
    К моменту изучения темы «Квадрат» учащимся знакомы такие виды четырехугольников как прямоугольник, ромб и их свойства. Прошу учащихся сформулировать определение квадрата. На что они дают два разных определения: «Квадратом называется прямоугольник, у которого все стороны равны» или «Квадратом называется ромб, у которого все углы прямые». Оба определения верные. Обсуждаем, почему имеет право быть каждое из них.

  4.  Создание проблемных ситуаций через умышленно допущенные учителем ошибки

Пример №7  Тема «Линейные уравнения с одной переменной» (6 класс)                                         

 Решаю быстро уравнение:

 (3х + 7) × 2 – 3 = 17

 6х + 14 – 3 = 17

 6х = 17 – 14 – 3

 6х = 0

 х = 0

        При проверке ответ не сходится.  Проблемная ситуация. Ищем ошибку. Дети решают проблему.

5.     Создание проблемных ситуаций  через  противоречие нового материала старому, уже известному

Пример № 8    Тема «Формулы сокращённого умножения» (7 класс)

 Вычисляем       (2 × 5)²= 2² × 5² = 100

                          (3 × 4)²= 3² × 4² = 9 × 16 = 144

                          (5 : 6)² = 5² : 6² = 25 : 36

                          (3 + 4)² = 3² + 4² = 9 + 16 = 25 

 Попробуйте сосчитать по-другому.

 ( 3 + 4)² =7² = 49

 Проблемная ситуация создана. Почему разные результаты?

 ( 3 +4)² ≠ 3² + 4²

6.     Создание проблемных ситуаций через выполнение небольших исследовательских заданий.

 

Пример№9. Тема «Длина окружности» (6 класс)

   Ещё древние греки находили длину окружности по формуле    - это диаметр окружности.

Вопрос: а что же такое ?

Работаем в парах, выполняя необходимые измерения.

1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить более точный результат, нужно это проделать несколько раз. Занесите данные в следующую таблицу.

С1	С2	С3	С сред.

 

2.Измерьте диаметр стакана линейкой. Данные занесите в таблицу.

3.Найдите значение , как неизвестного множителя. Можно пользоваться калькулятором.

4.Каждой паре занести вычисленное значение  в таблицу на доске.

                                                       Полученные значения

1 пара	2 пара	3 пара
среднее арифметическое = ( 1 пара +2 пара +3 пара):3             Значение  от 3,1 до 3,2

 

 это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой.

=3,1415926…

Для того, чтобы легче запомнить цифры  надо сосчитать количество букв в каждом слове высказывания: «Это я знаю и помню прекрасно» или «Нужно только постараться и запомнить всё как есть: три, четырнадцать, пятнадцать, девяносто два и шесть!»

В дальнейшей работе мы будем использовать значение  =3,14

Исследование проведено. На уроке кроме исследовательской работы удачно использовалась работа в парах. Сотрудничество и взаимопомощь  принесли  желаемый  результат. Проблема решена.

 

7.Создание проблемных ситуаций через использование занимательных заданий.

Пример №10.  Тема: «Линейная функция»(7 класс)

Обычная форма задания: функция задана формулой найдите значение функции при x = 0, 7, -5, 1.

Занимательная форма задания: Приглашаю к доске ученика, даю ему карточку, на которой  написано. На доске заготовлена таблица:

 Ученик из класса называет какое-нибудь значение х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение у. Затем другой ученик из класса называет другое значение х и ученик у доски проделывает те же операции. Задача класса – “угадать” формулу, записанную на карточке. Проблемная ситуация создана. Выигрывает тот ученик, который первый назовет формулу.

 

Пример №11.  Тема: «Координатная плоскость» (6 класс)

В начале урока учитель демонстрирует классу хорошо знакомые предметы, например, шахматную доску, глобус, билет в театр. Учащимся предлагается ответить на вопрос: «Что объединяет все эти предметы?».

Поиск ответа можно начать с чтения отрывка из первой главы романа Ж. Верна «Дети капитана Гранта».

После окончания чтения  учитель выстраивает подводящий диалог:

·        Почему героям романа пришлось преодолеть столько километров пути в поисках пропавшей экспедиции? – Не известно точное местонахождение героев.

·        Как в географии описывается точно местонахождение объекта? – Указываются широта и долгота (географические координаты).

·        Что же общего у предметов, которые были предъявлены вам в начале урока? – Они позволяют определить положение (место) человека в зрительном зале или фигуры на шахматной доске.

Затем учитель предлагает вернуться к математике и попробовать провести параллель между объектами в географии и математике.

·        Как описать положение точки на плоскости? – Ввести координаты на плоскости.

·        Какова же тема урока? - Координаты на плоскости. (На доске появляется тема урока)

·        Географические координаты (широта и долгота) – это воображаемые окружности на поверхности земного шара. Что можно взять на плоскости вместо окружностей? – Прямые.

·        Сколько прямых и каково их взаимное расположение? – Две пересекающиеся прямые.

В заключение диалога учитель подводит итог: «Наверное, таким же образом рассуждал ещё один великий француз – Рене Декарт, когда предложил использовать две взаимно перпендикулярные прямые для введения координат на плоскости. С тех пор математики всего мира так и говорят – декартова система координат». (На слайде демонстрируется   портрет Декарта)

Далее на уроке рассматриваются типовые задачи (нахождение координат точки и построение точки по заданным координатам) и выполняется задание «Рисуем по координатам».

В качестве домашнего задания можно предложить учащимся творческую работу «Зашифруй рисунок», а также привести примеры из повседневной жизни, где мы встречаемся с координатами на плоскости (артиллерия, домашний адрес).

Пример № 12. Тема: «Теорема, обратная теореме Пифагора» (8 класс)

Урок начинается с рассказа о египетском треугольнике.

Развитие геометрии было связано в том числе и с потребностями строительной техники. Так, еще древним египтянам требовалось умение строить прямой угол. Этим занимались работники – «натягиватели веревки», которые назывались так потому, что построение осуществлялось с помощью веревки с завязанными узелками,  длина которой равнялась (3+4+5) единиц.

В землю вбивались три кола, на которые и натягивалась веревка, так чтобы получился треугольник со сторонами 3, 4 и 5 единиц. Египтяне знали, что угол между меньшими сторонами будет прямым. Такой треугольник в математике до сих пор называется египетским. (На доске – рисунок прямоугольного треугольника со сторонами 3, 4 и 5 единиц)

         Учитель предлагает классу убедиться в верности построений древних египтян с помощью теоремы, обратной теореме Пифагора.

В данный момент урока уместно еще раз вспомнить:

·        о строении любой теоремы (Дано – доказать; Условие – заключение),

·        о связи между формулировками прямой и обратной теорем (условие и заключение теорем «меняются местами»),

·        формулировку теорему Пифагора.

А затем попросить учащихся самостоятельно сформулировать обратную теорему.

Обычно учащиеся дают следующую формулировку: «Если квадрат гипотенузы равен сумме квадратов катетов, то треугольник прямоугольный».

В ходе беседы выясняем, что:

·        использовать термины «катет» и «гипотенуза» нельзя,

·        вспоминаем, что гипотенуза – большая сторона прямоугольного треугольника,

·        заменяем слово «гипотенуза»   словами «большая сторона», а «катеты» - на  слова «две другие стороны».

         Учащиеся корректируют данную ими ранее формулировку теоремы и получают: «Если квадрат большей стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный».

         Осталось только воспользоваться данной формулировкой, чтобы убедиться в том, что треугольник со сторонами 3, 4 и 5 будет действительно прямоугольным.

Пример №13. Тема: «Теорема Виета» (8 класс) 

         Урок начинается с исторической зарисовки (на слайде – портрет Франсуа Виета).

XVI век. Франция. Адвокат и советник короля Генриха III Франсуа Виет, будучи выдающимся математиком, сумел раскрыть ключ шифра, состоявшего из 500 знаков, с помощью которого враги короля вели переписку с испанским двором. Но среди математиков Виет известен своей теоремой о свойствах корней квадратного уравнения.

         Далее учащимся предлагаются задания:

1) Запишите данные уравнения в тетрадь и подчеркните те из них, которые имеют общее отличие от остальных. Укажите это отличие.

а) - 5х - 6х + 1 = 0;  б) 6d - 5d – 1 = 0;         в) х - 5х + 6 = 0;

 

      г) 7х - 6х + 2 = 0;   д) z + 8z + 15 = 0;        е) t - 3t – 4 = 0.

После выполнения этого задания даем определение приведенного квадратного уравнения, записываем его в общем виде, вводим обозначение коэффициентов.

2) Решите приведенные квадратные уравнения и найдите сумму и произведение корней.

         На доске записываем только условие приведенного квадратного уравнения, сумму и произведение корней:

а) х - 5х + 6 = 0 Ответ: х + х = 5, х · х = 6

б) z + 8z + 15 = 0 Ответ: z + z = - 8, z · z = 15

в) t - 3t – 4 = 0 Ответ: t + t = 3, t· t = - 4

3) Сравните полученные числа и коэффициенты! Что интересного вы заметили?

     Запишите это свойство для уравнения х + px + q = 0.

На слайде:  х + px + q = 0

                   х + х =  - p,

                      х · х = q

Далее учитель подводит итог работы: именно эту зависимость для любого квадратного уравнения и увидел Франсуа Виет.

На слайде: ax + bx + c = 0 | : a

     x + x +  = 0

Теорема Виета для квадратного уравнения общего вида:

х + х = - ,

х · х =

Звучат стихи Александра Гуревича, посвященные теореме Виета:

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого?

Умножишь ты корни – и дробь уж готова,

В числителе «с»,  в знаменателе «а».

А сумма корней тоже дроби равна,

Хоть с минусом дробь эта, что за беда?

В числителе «b», в знаменателе «а»!

Пример № 14. Тема: «Формулы сокращённого умножения»(7 класс)

Преступники украли в банке большую сумму денег. Их поймали, но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её  показатель. Экспертам удалось узнать основание степени. Это число 597. Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения 

( 2y +1)² – 4y² =9

y = 2

597² = (600 – 3)² =600² -2 · 600 · 3 + 3² = 360000 – 3600 + 9 =356409

 

 Пример № 15. 

Тема «Сумма n-первых членов арифметической прогрессии» (9 класс) 

Начать урок можно с исторической зарисовки о детстве великого математика Карла Гаусса.

Рассказывают, что в начальной школе, где учился мальчик Карл Гаусс, ставший потом знаменитым математиком, учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал детям задание - вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Он увидел, что…

На доске:

1 + 2 + 3 + …+ 98 + 99 + 100 = (1+100)+(2+99)+(3+98)+…+(50+51) = 101·50 = 5050

Подводящий диалог:

Попробуем взглянуть на условие задачи с высоты наших знаний:

·        Что собой представляет последовательность чисел  1, 2, …,  100? - Арифметическую прогрессию, первый член которой равен 1, n-член равен 100, а разность равна 1.

·        Что требуется  найти? - Сумму 100 первых членов. (Вводим обозначение. На доске: S- сумма n-первых членов арифметической прогрессии).

·        Какова будет тема урока? - Сумма n-первых членов арифметической прогрессии.

На доске появляется тема урока и условие задачи:

Дано: (a) – арифметическая прогрессия,

             а = 1, а = 100,  n = 100

 Найти: S.

·        Попробуйте связать числа 101 и 50 с данными «нашей задачи». Что интересного вы заметили? - 101 = а + а, 50 = .

·        Запишите формулу суммы n-первых членов геометрической прогрессии. –

      S = (а + а)·  = ·n      

·        Существует еще одна формула суммы n-первых членов геометрической прогрессии, которую вы получите, если  воспользуетесь формулой n-члена арифметической прогрессии а = а+ (n – 1)·d. -  S = ·n      

На доске появляются формулы:

 S = (а + а)·  = ·n      (1)

S = ·n    (2)

Главный фактор занимательности – это приобщение учащихся к творческому поиску, активизация их самостоятельной исследовательской деятельности, так как уникальность занимательной задачи служит мотивом к учебной деятельности, развивая и тренируя мышление вообще и творческое, в частности.                                                                                                                                           

 

 Пример № 16

Тема «Сумма n-первых членов геометрической прогрессии» (9 класс)

Учитель начинает урок с индийской легенды об изобретателе шахмат.

Рассказывают, что индийский царь Шерам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат: за первую клетку шахматной доски 1 зерно, за вторую – 2, за третью – 4, за четвертую – 8, и так до 64 клетки. Царь приказал немедленно выдать столь «ничтожную» по его мнению, награду, взяв зерно из кладовых дворца. Каково же было его удивление, когда на следующее утро он узнал, что в кладовых дворца нет требуемого количества зерен. Не оказалось его и во всем царстве Шерама! А мудрецы, которым царь велел исчислить требуемое количество зерен, утверждали, что если бы   удалось засеять пшеницей площадь всей поверхности Земли, считая и моря, и океаны, и горы, и пустыни, и получить удовлетворительный урожай, то, пожалуй, лет за пять Шерам смог бы рассчитаться с просителем. Как вы считает – стоило  ли ему смеяться?

Какое же количество зерен потребовал изобретатель шахмат? Попробуйте и вы ответить на этот вопрос! (Учащимся дается 5 минут на решение задачи.)

Побуждающий диалог:

·        Вы смогли выполнить задание? В чем затруднение? – Нет. Очень долго считать.

·        Какой возникает вопрос? – Нельзя ли упростить решение?  Нет ли формулы?

·        Давайте «переведем» содержание задачи на язык математики, чтобы понять какую формулу мы хотим получить. – Число зерен, которые потребовал мудрец за каждую клетку, образуют геометрическую прогрессию, в которой всего 64 члена (по числу клеток шахматной доски), первый член равен 1, а знаменатель 2.  Нужно найти  сумму n-первых членов.

·        Какова же тема урока? - Формула суммы n-первых членов геометрической прогрессии.

На доске появляется тема урока и условие задачи.

Дано: (b) – геометрическая прогрессия,

           b = 1, b = 2, q = 2, n = 64

Найти: S

Далее учащиеся под руководством учителя выводят формулу суммы n-первых членов геометрической прогрессии.

 Пример № 17.   Тема «НОК и НОД»  (6 класс)

В легенде рассказывается, что, когда один из помощников Магомета – мудрец Хозрат Али садился на коня, подошедший человек спросил его:

- Какое число делится без остатка на 2, 3, 4, 5, 6, 7, 8, 9?

Мудрец ответил:

- Умножь число дней в неделе на число дней в месяце (считая, что в месяце 30 дней) и на число месяцев в году. Прав ли Хозрат Али? Почему?

 

Таким образом, технология проблемного обучения на уроках математики - это способ достижения цели через детальную разработку проблемы, которая должна завершиться вполне реальным, осязаемым практическим результатом. 

Результатом моего опыта можно считать:

- рост мотивации к изучению предмета; 

- увеличение количества участников и победителей олимпиад, математических конкурсов;

- рост качества знаний учащихся

- методическая разработка серии уроков по алгебре в 10 классе.