ПРИНЦИПЫ «ГИБКОЙ» ПЕДАГОГИЧЕСКОЙ ТЕХНОЛОГИИ ПРОБЛЕМНО-МОДУЛЬНОГО ОБУЧЕНИЯ (НАУЧНО-МЕТОДИЧЕСКАЯ СТАТЬЯ).

Павлов Александр Константинович, -

генеральный директор МИНИОДСПК «ПЕДКАМПУС»
(Российская Федерация, г. Москва – г. Санкт-Петербург –

г. Петрозаводск -  г. Мурманск), -

доктор педагогических наук, профессор,

член-корреспондент, академик МАНЭБ,

Лауреат премии им. М.В. Ломоносова,
Заслуженный деятель науки РФ

ПРИНЦИПЫ «ГИБКОЙ» ПЕДАГОГИЧЕСКОЙ ТЕХНОЛОГИИ ПРОБЛЕМНО-МОДУЛЬНОГО ОБУЧЕНИЯ

(НАУЧНО-МЕТОДИЧЕСКАЯ СТАТЬЯ)

     Эффективность процесса обучения трудно обеспечить классическими или отдельными новыми методами. Необходима взаимосвязь различных методов обучения, их взаимодополнение и взаимоусиление. Иными словами, современный этап развития дидактики наряду с разработкой новых технологий обучения требует их интеграции с уже известными, что позволяет создавать «полифонические» дидактические системы. Преимущество таких систем перед «монофоническими» заключается в том, что они аккумулируют достоинства интегрируемых теорий и образуют целостность, позволяющую выходить на новый качественный уровень решения педагогических задач.

     Именно поэтому, приняв целевую установку на формирование и развитие профессиональной компетентности специалиста, мы предприняли попытку смоделировать технологию проблемно-модульного обучения, интегрирующую достижения теории проблемного обучения, концепции «сжатия» знаний и модульного обучения в условиях взаимосвязи общего и профессионального образования.

     Перестройка процесса обучения на проблемно-модульной основе позволяет:

1) интегрировать и дифференцировать содержание обучения путём группировки проблемных модулей учебного материала, обеспечивающих разработку курса в полном, сокращенном и углубленном вариантах;

2) осуществлять самостоятельный выбор учащимися того или иного варианта курса в зависимости от уровня облученности и обеспечивать индивидуальный темп продвижения по программе;

3) использовать проблемные модули в качестве сценариев для создания педагогических программных средств;

4) акцентировать работу преподавателя на консультативно-координирующие функции управления познавательной деятельностью учащихся;

5) сократить курс обучения без особого ущерба для полноты изложения и глубины усвоения учебного материала на основе адекватного комплекса методов и форм обучения.

     Наряду с перечисленным, специфику проблемно-модульной технологии обучения отражают следующие основные принципы её построения:

1) системное квантование;

2) мотивация;

3) проблемность;

4) модульность;

5) когнитивная визуализация;

6) опора на ошибки;

7) экономия учебного времени.

     Рассмотрим содержание каждого из названных выше принципов.

     Принцип системного квантования вытекает из требований теорий сжатия учебной информации, к которым можно отнести элементы содержательного обобщения (В. В. Давыдов), теорию укрупнения дидактических единиц (П.М.Эрдниёв) концепцию инженерии знаний (Д. А. Поспелов и др.). Кроме того, этот принцип предполагает учёт следующих психолого-педагогических закономерностей:

1) учебный материал большого объёма запоминается с трудом;

2) учебный материал, компактно расположенный в определённой системе, облегчает восприятие;

3) выделение в изучаемом материале смысловых опорных пунктов способствует эффективности его запоминания.

     При этом следует подчеркнуть, что требования этих закономерностей не должны идти вразрез с принципами научности и фундаментальности и тем самым нарушать логику учебного предмета. Принцип системного квантования обеспечивается соответствующим структурированием учебной информации в проблемном модуле.

Общая структура проблемного модуля представлена на рис. 1.

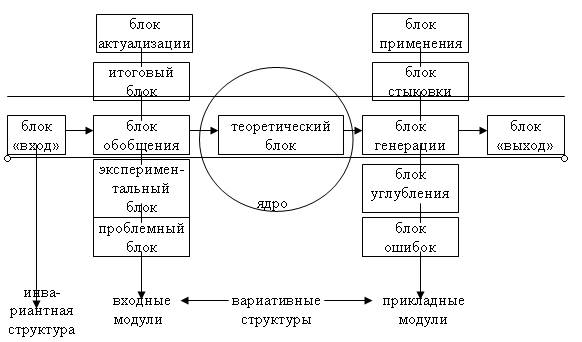
Рис. 1. Общая структура проблемного модуля

     Основной дидактической функцией блока «вход» является осуществление актуализирующего контроля. Главная особенность этого контроля заключается не только в том, что его прохождение означает своего рода выдачу «пропуска» в проблемный модуль, но прежде всего в том, что тестовые задания предполагают актуализацию тех опорных знания и способов действий, которые необходимы для усвоения содержания всего проблемного модуля. Наряду с этим актуализирующий контрольный тест снабжен соответствующим указателем, отсылающим учащегося к тому учебному материалу, знание которого нужно для успешного выполнения данного теста. В тех же случаях, когда обращение к учебному материалу не дает должного эффекта, учащийся может получить консультацию у преподавателя. Такая компоновка входного блока соответствует структуре контролирующей учебной программы, используемой в АОС.

     Принцип проблемности отражает требования психолого-педагогической закономерности, согласно которой введение таких стимулирующих звеньев, как проблемная ситуация и практическая направленность, повышает эффективность усвоения учебного материала. Этот принцип реализуется постановкой и решением укрупнённых проблем, а также служит исходным положением для конструирования педагогики проблемного модуля и его элементов, в частности для учебных элементов теоретического блока проблемного модуля. Требования принципа проблемности отражаются в проблемном блоке при постановке проблемы и выдвижения гипотез, в теоретическом блоке - при обосновании выдвинутых гипотез и в блоке стыковки - при решении проблемы и проверке её решения.

     Принцип когнитивной визуализации вытекает из психолого-педагогической закономерности, согласно которой эффективность усвоения повышается, если наглядность в обучении выполняет не только иллюстративную, но и когнитивную функцию. Именно поэтому составными компонентами проблемного модуля являются когнитивно-графические учебные элементы (блок-рисунки), выполненные в цвете. Выбор рисунка в качестве главного элемента проблемного модуля далеко не случаен. В первую очередь он положительно влияет на развитие зрительной памяти и пространственного мышления учащихся. Тем самым блок-рисунок помогает подключить к процессу усвоения учебного материала богатый потенциал образного правого полушария мозга, которого так не хватает при традиционном «левополушарном» обучении. Далее, блок-рисунок, компактно иллюстрирующий содержание учебного материала, способствует формированию у учащихся системности знаний. Немаловажное значение имеет его цветовое представление. Помимо того, что блок-рисунок, выполненный в цвете, служит одним из средств эстетического воспитания учащихся, он выгодно отличается от чёрно-белого блок-рисунка. Опыт применения блок-рисунка свидетельствует о следующей устойчивой зависимости: эффективность восприятия и запоминания учебной информации попытается, если блок-рисунок представлен в цвете.

     Принцип опоры на ошибки направлен на систематическое создание в процессе обучения ситуаций на поиск ошибок. Требования этого принципа находят отражение в историческом блоке и блоке ошибок. Этот принцип направлен также на разработку дидактических материалов и средств, ориентированных на формирование, развитие аппарата предвосхищения (акцептора результатов действия) в структуре функциональной системы психической деятельности обучаемых.

     Немаловажная роль принципа опоры на ошибки заключается в ориентации обучения на формирование критичности мышления - составного компонента профессиональной компетентности специалиста.

     Принцип экономии учебного времени направлен на обеспечение резерва времени для индивидуальной и групповой самостоятельной работы учащихся. Согласно исследованиям в области проблемно-модульного обучения, оно приносит до 30% экономии учебного времени без ущерба для глубины и полноты изучения материала.

     Развитие современной педагогики ориентируется на проектирование «гибких» педагогических технологий. «Гибкость» в педагогике проявляется в переходе от единой школы к многообразию их новых типов (гимназий, лицеев, колледжей), от использования единых учебников - к выбору альтернативных учебников и учебных пособий, от единых программ и учебных планов - к их варьированию посредством выделения базовых (обязательных) предметов и предметов по выбору, от преимущественно коллективных форм организации обучения – к индивидуальным формам и обучению в малых группах, от единого уровня общеобразовательной подготовки к диалектически взаимосвязанной интеграции и дифференциации содержания обучения, от застывшей формы обучения - урока - к многообразию форм обучения, от традиционных методик обучения — к их полифоническому разнообразию и т. д. Комплексное решение этих вопросов - актуальнейшая проблема современной педагогики.

     Не претендуя на целостное решение этой проблемы, мы сосредоточили свои усилия на одном из вариантов проектирования «гибкой» технологии обучения, базирующейся на проблемно-модульном подходе. По нашему мнению, данный подход обладает широкими возможностями и богатым потенциалом в обеспечении, именно гибкости процесса обучения.

     Потенциал предлагаемой нами технологии проблемно-модульного обучения заложен в теоретических концепциях, составляющих методологическую основу технологии. В первую очередь, - это общая теория функциональных систем и ведущие её принципы: системного квантования, модульности и проблемности. Во-вторых, – это интеграция дидактически адаптированных теорий, вытекающих из перечисленных принципов: теории «сжатия» знаний, теории проблемного и модульного обучения. Целостным качеством, возникающим в результате интеграции этих теорий, и является гибкость, а технология, сконструированная на основе данной интеграция, получила название «гибкой» технологии проблемно-модульного обучения.

Литература

1. Анохин П. К. Принципиальные вопросы общей теории функциональных систем // Принципы системной организации функций. — М., 1973. - С. 5-61.

2. Балашов Ю. К., Рыжов В. А. Профессиональная подготовка кадров в условиях капитализма. - М.: Высшая школа, 1987.

3. Балк М. Б., Балк Г. Д. О привитии школьникам навыков эвристического мышления // Математика в школе. - 1985. - № 2. -С. 55-60.

4. Башмаков М. И. Математика. - М.: Высшая школа, 1987.

5. Бескин Н.М. Методика геометрии. - М.; Л.: Учпедгиз, 1947.

6. Беспалько В. П. Слагаемые педагогической технологии. -М.: Педагогика, 1989.

7. Боголюбов В. И. Педагогическая технология: эволюция понятия // Сов. педагогика. - 1991. - № 9. - С. 123-128.

8. Б р а д и с В. М. Методика преподавания математики в средней школе. - М.: Учпедгиз, 1954.

9.Буш Г. Я. Основы эвристики для изобретателей. - Рига, 1977.

10. Васильева Т. В. Модули для самообучения // Вестник высшей 'школы. - 1988. - № 6. - С. 86-87.

11. Вевдровская Р. Б. Очерки истории советской дидактики. -— М.: Педагогика, 1982.

12.Вербицкий А. А. Активное обучение в высшей школе: контекстный подход. - М.: Высшая школа, 1991.

13. Гареев В. М. и др. Принципы модульного обучения // Вестник высшей школы. - 1987. - № 8.

14. Германович П. Математика в школах профотбора // Просвещение на транспорте. - 1927.-№ 7-8.

15. Гнеденко Б. В., Черкасов Р. С. О курсе математики в школах Японии // Математика в школе. - 1988. - № 5.

16. Грегори Р. Л. Разумный глаз. - М.: Мир, 1972.

17. Давыдов В. В. Проблемы развивающего обучения. - М.: Педагогика, 1986.

18.3арецкий М. И. За качество урока в школе ФЗУ // За промышленные кадры. - 1933. - № 12. 19. Зенкин А. А. Когнитивная компьютерная графика. - М.: Наука, 1991.

20. Кандрашина Е. Ю. и др. Представление знаний о времени и " пространстве в интеллектуальных системах / Под ред. Д. А. Поспелова - M.: Мир, 1989.

21. Кларин М. В. Педагогическая технология в учебном процессе: Анализ зарубежного опыта. - М.: Знание, 1989.

22. Кудрявцев В. Т. Проблемное обучение: истоки, сущность, перспективы. - М.: Знание, 1991.

23. Ландшеер В. Концепция "минимальной компетентности" // Перспективы: вопросы образования. - 1988. - № 1.

24. Ланков А. В. Математика в трудовой школе: Очерки по методике математики. - М.: Работник просвещения, 1924.

25. Лебединцев К. Ф. Введение в современную методику математики. - Киев: Гос. изд-во Украины, 1925.

26. Лобачевский Н. И. Научно-педагогическое наследие... / Отв. ред. П. С. Александров и Б. Л. Лаптев. - М.: Наука, 1976.

27. Марев И. Методологические основы дидактики. - М.: Педагогика, 1987.

28. Махмутов М. И. Проблемное обучение: Основные вопросы теории. - М.: Педагогика, 1975.

29. М а х м у т о в М. И. Современный урок. - М.: Педагогика, 1985.

30. Метельский Н. В. Психолого-педагогические основы дидактики математики. - Минск: Высшая школа, 1977.

31. Методика преподавания математики в средней школе: Общая методика / Сост. Р. С. Черкасов, А. А. Столяр. - Ml: Просвещение,

32. Минский М. Фреймы для представления знаний. - М.: Энергия,

33. Моделирование педагогических ситуаций / Под ред. Ю. Н. Кулюткина, Г. С. Сухобской. - М.: Педагогика, 1981.

34. Моро М. И., Пышкало A.M. О. совершенствовании методов обучения математике // О совершенствовании методов обучения математике. - М.: Просвещение, 1978. - С. 7-51.

35. Оконь В. Введение в общую дидактику. - М.: Высшая школа, 1990.

36. Петрусинский В. В. Автоматизированные системы интенсивного обучения. - М.: Высшая школа, 1987.

37. Пойа Д. Математическое открытие. - М.: Наука, 1976.

38. Пойа Д. Математика и правдоподобные рассуждения. — М.: Наука, 1975.

39. Приобретение знаний / Пер. с япон. / Под ред. С. Осуги, Ю. Саэки. - М.: Мир, 1990.

40. Представление и использование знаний / Пер. с япон. / Под ред. X. Уэно. - М.: Мир, 1989.

41. Программа-минимум единой трудовой школы. Вторая ступень. - Л., 1925.

42. Рабочая книга по математике: Пособие для изучения математики по лабораторному плану и по аккордной системе / Под ред. Г. А. Понперека. - Ч. 1-3. - М.: Госиздат, 1923.

43. Рогинский В. М. Азбука педагогического труда. - М.: Высшая школа, 1990.

44. Рыбаков А. Система проектов в школе ФЗУ // Жизнь рабочей Школы. - 1930. - № 1. - С. 30-35.

45. Сагалович Г. Математика в комплексной системе преподавания в школе первого концерта. - Минск, 1928.

46. Салмина Н. Г. Знак и символ в обучении. - М.: Изд-во МГУ, 1989.

47. Системный анализ процесса мышления / Под ред. К. Д. Судакова. - М.: Медицина, 1989.

48. Третьяков М. Иллюстрированныйметод на уроках математики //Жизнь рабочей школы. - 1929. - № 5. - С. 41-48.

49. Ф о р м ы и методы общеобразовательной подготовки / Под ред. М. И. Махмутова. - М.: Педагогика, 1986.

50. Хамблин Д. Формирование учебных навыков. - М.: Педагогика, 1986.

51. Цирюльников А. Чему учиться: Заметки на полях истории педагогики // Учительская газ. - 1988. - 19,20,21 апр.

52. Чередов И. М. Формы учебной работы в средней школе: Кн. для учителя. - М.: просвещение, 1988.

53. Черкасов Р. С, Отани М. Новая программа по математике в школах Японии // Математика в школе. - 1991. - № 1. - С. 73-75.

54. Шатихвв Л.Г. Структурные матрицы и их применение для исследования систем, - М.: Машиностроение, 1991.

55.Шохор-Троицкий СИ. Геометрия на задачах: (Основной курс). - М.: Изд-во т-ва И. Д. Сытина, 1913.

56. Эйнштейн А. Физика, и реальность. - М.: Наука, 1965.

57. Эделмак Дж., Маунткастл В. Разумный мозг. - М.: Мир, 1981.

58. Эрдниев П. М. Системность знаний и укрупнение дидактической единицы // Сов. педагогика. - 1975. - № 4. - С. 72-80.

59. Юцявичене П. А. Теория и практика модульного обучения. Каунас:Швиеса, 1989.

60. Ястребинецкий Г. А., Блох А. Я. О математическом образовании в средних школах США. // Математика в школе. - 1988. - J* 4. - С. 73-76.

61. Вi11stein R., Lott T. Mathematics for Liberal arts: A problem solving approach. - Menlo Park: Benjamin Cummings, 1986.

62. В1аnк W. Е. Handbook for developing Competency-Based Training Programs. - New-Jersey: Prentice Hall, 1982.

63. Bloom B. S., Broder L. Problem solving processes of college students. Supplementary Education Monograph. - Chicago: University of Chicago Press, 1950.

64. Bransford J. D., Stein S. B. The IDEAL problem solver.-" N-Y.: W.H. Freeman & C, 1984. -U .

65. Вгite11 Т. К. Competency and Exellence Minimum Competency Achivment Testing/Taeger R. M. & Title C.K. (eds). - Berkeley, 1980. -P. 23-29.

66. Сuгсh C. Modular courses in British higher education // A critical yassesment in higher education bulletin. - 1975, Vol. 3. - P. 65-84.

67. Goldschmidt В., Goldschmidt M. Modular Instruction in Higher Education // Higher Education. - 1972. - № 2. - P. 15-32.

68.International Annual on educational technology. - London, 1978-1979.

69. Кilpatriс Т. A retrospective account of the past twenty-five years of research on teaching mathematical problem solving // Teaching and Learning Mathematical Problem Solving: Multiple research perspectives. -London: LEA, 1985. - P. 1-16.

70. Lange V. Geometry in modules: Teacher's Manual. - London: Addison-Wesley P. C, 1986.

71. MadiganS., Rоuse M. Picture memory and visual-generation processes//The American Journal of Psychology.-1974, Vol. 87.-P. 151-158.

72. Modularization and progression: Issues in the 14-19 curriculum: Working Paper. - London: London Univ. Press. - 1989. - № 6.

73. Modularization and the new curricular. - London: FESC Report, 1986; Vol. 19. - № 4.

74. Moon B. Introducing the modular curriculum // The modular curriculum. - London, 1988. - P. 9-21.

75. Noddings N. Small groups as a setting for research on mathematical problem solving // Teaching and Learning Mathematical problem solving. -London; 1985. - P. 345-360.

76. Riss1and E. L. Artificial intelligence and the learning of mathematics: A tutorial sampling // Teaching and Learning Mathematical-problem solving. - London, 1985. - P. 147-176.

77. Russell J. D. Modular Instruction // A Guide to the Design, Selection, Utilization and Evaluation of Modular Materials. - Minneapolis; BPC, 1974.

78. Sсhoenfeld A. H. Mathematical problem solving. - London: Academic Press, 1985.

79.Watkins P. Modular approaches to the secondary curriculum // SCDC. - London, 1986. - P. 12-18.

86. Барабан М.А. О проведении уроков "Анализ контрольной работы" // Математика в школе. - 1988. - № 3. - С. 24-25.

81. Башмаков М.И., Резник Н.А. Развитие визуального мышления на уроках математики // Математика в школе. - 1991. -М 1. - С 4-8.

82. Векслер С. И. Найтии преодолеть ошибку // Математика в школе. - 1989. - № 5. - С. 40-42.

83. Вивюрский В.Я. Обнаружение и исправление ошибок по химии//Сред. спец. образование. - 1989. - № 1. - С. 22-23.

84. 3ив Б. Г. Быстротечные минуты урока // Математика в школе. - 1988. - № 3. - С. 13-17.

85. Методика блочно-модульного обучения / Под ред. О.Е. Лисейчикова и М.А. Чошанова. - Краснодар: Сов. Кубань, 1989. - 123 с.

86. Тетерина Д. Д. Модульная система изучения органической химии//Специалист. - 1992. -№ 3. - С. 5-6.

87. Урок физики в современной школе: Творческий поиск учителей / Сост. Э.М. Браверман. Под ред. В.Г. Разумовского. - М.: Просвещение, 1993.- 288 с

88. Эрдниев П.М. Укрупнение дидактических единиц как технология обучения. - Ч. 1. - М.: Просвещение, 1992. - 175 с.