ПРОБЛЕМНО-МОДУЛЬНОЕ ОБУЧЕНИЕ КАК «ГИБКАЯ» ПЕДАГОГИЧЕСКАЯ ТЕХНОЛОГИЯ (НАУЧНО-МЕТОДИЧЕСКАЯ РАЗРАБОТКА).

Павлов Александр Константинович, -

генеральный директор МИНИОДСПК «ПЕДКАМПУС»
(Российская Федерация: г. Москва – г. Санкт-Петербург –

г. Петрозаводск -  г. Мурманск), -

доктор педагогических наук, профессор,

член-корреспондент, академик МАНЭБ,

Лауреат премии им. М.В. Ломоносова,
Заслуженный деятель науки РФ

ПРОБЛЕМНО-МОДУЛЬНОЕ ОБУЧЕНИЕ КАК «ГИБКАЯ» ПЕДАГОГИЧЕСКАЯ ТЕХНОЛОГИЯ

(НАУЧНО-МЕТОДИЧЕСКАЯ РАЗРАБОТКА)

     Одна из основных целей учебной подготовки - в формировании и развитии профессиональной компетентности специалиста. Достижение этой цели требует разработки и применения соответствующей технологии обучения. Применив комплекс методов научно-педагогического исследования (критический анализ различных педагогических технологий, метод моделирования, методы системного анализа содержания образования, метод системогенеза профессиональной деятельности и др.) и изучив отечественный и зарубежный опыт общеобразовательной подготовки, мы пришли к выводу, что достижение указанной цели может быть осуществлено в результате интеграции «усилий» трёх ведущих факторов: «сжатия», модульности и проблемности и построения на этой основе новой педагогической технологии - проблемно-модульного обучения.

     «Сжатие», модульность и проблемность направлены на обеспечение мобильности знания в структуре общеобразовательной компетентности учащегося, проблемность, прежде всего, ориентирована на развитие его критического мышления, а проблемность в сочетании с модульностью обеспечивает гибкость в применении методов деятельности. Схема целевой ориентации технологии проблемно-модульного обучения изображена на рис. 3.

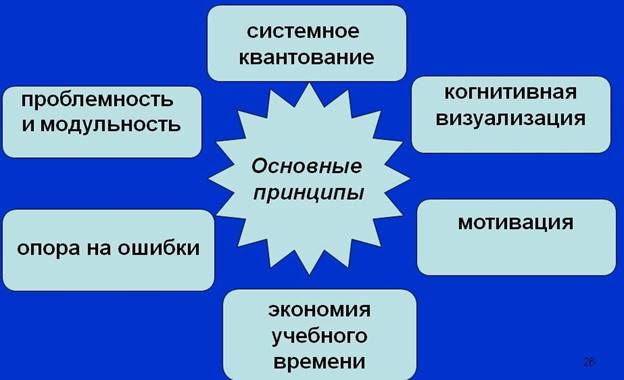
Рис. 1. Целевая ориентация технологии проблемно-модульного обучения

     Что же представляет собой технология проблемно-модульного обучения?

     Проблемно-модульное обучение имеет свои корни, как в педагогической теории, так и в практике. Исходной методологической позицией построения технологии проблемно-модульного обучения является общая теория фундаментальных, систем (Л. Берталанфи, П. К. Анохин, К. В. Судаков и др.), согласно которой весь континуум мыслительной деятельности человека, доминирующей мотивацией которой выступает постановка и решение личностно-значимой проблемы, может быть разделён на системные «кванты». Принцип системного квантования опирается на модульную организацию коры головного мозга человека (Г. Эделман, В. Маунткастл, Дж. Центагозай и др.). Принципы системного квантования, проблемности и модульности лежат в основе функциональных систем психической деятельности человека, выраженных различными знаковыми системами (языковыми, символическими, графическими и т. д.).

     Технология проблемно-модульного обучения базируется на единстве принципов системного квантования, проблемности и модульности. В дидактике эти принципы, к сожалению, рассматриваются не взаимосвязано. Принцип системного квантования составляет методологический фундамент теорий «сжатия» учебной информации. (Термин «сжатие» учебной информации здесь и в дальнейшем применяется для обозначения обобщения, укрупнения, систематизации, генерализации знаний с использованием достижений «инженерии знаний»).

     Принцип модульности является нейрофизиологической основой метода модульного обучения. Теоретическая значимость и новизна предлагаемой технологии состоит в том, что в ней принципы системного квантования, проблемности и модульности рассматриваются в целостности, в органическом единстве. Технология включает в себя целевую компоненту, ведущие принципы, специальные способы проектирования содержания обучения, систему задач и упражнений, конструирование дидактических материалов, рейтинговую систему контроля и оценки учебных достижений (рис. 2).

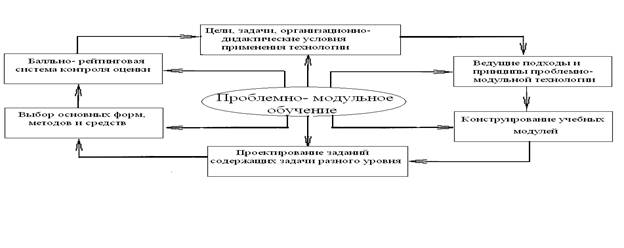
Рис. 2. Концептуальная модель педагогической технологии проблемно-модульного обучения

     Ведущей стержневой характеристикой технологии проблемно-модульного обучения является гибкость. Аналогично тому, как визитной карточкой современного высокотехнологического производства являются гибкие автоматизированные системы, так и эффективность педагогических технологий в настоящем и обозримом будущем во многом будет зависеть от их «гибкости» - способности оперативно реагировать и мобильно адаптироваться к изменяющимся научно-техническим и социально-экономическим условиям.

     Гибкость как стержневая характеристика пронизывает все основные компоненты технологии проблемно-модульного обучения. Именно поэтому следует различать: структурную гибкость, содержательную гибкость, технологическую гибкость.

     Структурная гибкость обеспечивается рядом моментов: от мобильности структуры проблемного модуля и ступенчатости проблемно-модульной программы до возможности проектирования гибкого расписания занятий и оборудования подвижной структуры учебного кабинета.

     Содержательная гибкость отражается, прежде всего, в возможности как дифференциации, так и интеграции содержания обучения. Эта возможность имеет место благодаря блочному и модульному принципу построения учебного материала в предлагаемой нами технологии.

     Технологическая гибкость обеспечивает процессуальный аспект проблемно-модульного обучения, включая вариативность методов обучения, гибкость системы контроля и оценки, индивидуализацию учебно-познавательной деятельности обучающихся.

     Гибкость выступает как целостное качество, образованное в результате интеграции слагаемых проблемно-модульного обучения.

     Рассмотрим каждую из составляющих предлагаемой технологии отдельно.

     Дидактически адаптированная конвенция инженерии знаний. Для того чтобы знание специалиста было мобильным, он должен быть способным обрабатывать накопленные знания, уметь добывать новые знания и использовать те и другие в своей практической деятельности. Таким образом, он должен быть своего рода инженером знаний.

     В последние годы возникла специальная отрасль информационной технологии – «инженерия знаний» (knowledge engineering), направленная на исследование проблем представления и использования знаний. Инженерия знаний (термин Э. Фейгенбаума) - это «область в теории искусственного интеллекта, которая занимается языками для представления знаний, методами пополнения знаний, процедурами проверки их корректности и непротиворечивости и, наконец, использованием знаний при решении различных задач и созданием практических систем для хранения и обработки знаний» [20].

     Может возникнуть вполне уместное сомнение: ведь общепризнано, что инженерия знаний имеет отношение к обучению интеллектуальных систем, а не к обучению человека. Как признают это сами исследователи теории инженерии знаний, есть несколько существенных аргументов в пользу того, что инженерия знаний имеет прямое отношение и к обучению человека [20, 39, 40, 76]. Во-первых, создатели интеллектуальных систем опираются на механизмы обработки и применения знаний человеком, используя при этом аналогии нейронных систем головного мозга человека. Во-вторых, пользователем интеллектуальных систем выступает человек, что предполагает кодирование и декодирование информации средствами, удобными пользователю, т. е. как при построении, так и при применении интеллектуальных систем учитываются механизмы обучения человека.

     Кроме того, из приведенного выше определения следует, что инженерия знаний содержит в качестве основных задач разработку языков и моделей представления знаний, методов их пополнения и использования при решении различных задач (компонент мобильности звания и гибкости метода в структуре компетентности), разработку процедур проверки корректности и непротиворечивости знаний (компонент критичности в структуре компетентности), решение которых предполагает формирование компонентов компетентности: мобильности знания, вариативности метода и критичности мышления как у разработчиков, так и у пользователей. Поэтому далеко не случайно привлечение концепции инженерии знаний для построения проблемно-модульной технологи обучения, направленной на формирование  и развитие общеучебной компетентности.

     В эпоху информационной насыщенности проблемы компоновки знания и оперативного его использования приобретают колоссальную значимость. С этой целью в русле концепции инженерии знаний рассматриваются всевозможные типы моделей представления знаний в «сжатом», компактном, удобном для использования виде. Среди них: логическая модель; продукционная модель; фреймовая модель; модель семантической сети [39,40].

     Примером логической модели служит символическая запись математических аксиом и теорем с использованием логики предикатов. В случае словесной записи 67 знаков, в логической модели - всего 15.

     Продукционная модель состоит из набора правил или алгоритмических предписаний для представления какой-либо процедуры решения задач. Чаще всего в продукционных моделях «сжатие» осуществляется через композицию продукций. Основатель теории фреймов М. Минский дает следующее определение: «Фрейм» (рамка) - это единица представления знаний, запомненная в прошлом, детали которой при необходимости могут быть изменены согласно текущей ситуации» [32]. Фрейм, как правило, состоит из нескольких ячеек — слотов, каждый из которых имеет свое назначение. При помощи фреймовой модели можно «сжимать», структурировать и систематизировать информацию в определенные таблицы, матрицы и т. д.

     Модель семантической сети опирается на представление знаний с использованием графов, блок-схем, рисунков и т. д.

     Эффективными способами «сжатия» учебной информации, помимо различных направлений инженерии знаний, могут служить приёмы из арсенала известных психолого-педагогических теорий содержательного обобщения и укрупнения дидактических единиц. П. М. Эрдниев не без основания утверждает, что «целеустремленное использование принципа укрупнения приносит до 20% чистой экономии учебного времени против общепринятых норм» [58, с. 72].

     Технологически «сжатие» учебной информации может быть достигнуто различными методическими приёмами, описание которых содержится не только в теории инженерии знаний, но и в исследованиях по формированию системности знаний учащихся, а также в работах учителей-практиков. Наиболее действенными зарекомендовали себя следующие методические приёмы: моделирование в предметной, графической и знаковой форме, укрупненное упражнение и сверх-символ, структурная блок-схема темы, опорный конспект, генеалогическое древо и т. д. Вместе с тем следует учитывать тот факт, что при осуществлении «сжатия» программного материала «наибольшая прочность освоения достигается при подаче учебной информации одновременно на четырёх кодах: рисуночном, числовом, символическом и словесном» [58, с. 79].

     Это положение является принципиальным при построении модели педагогической технологии проблемно-модульного обучения.

     Модульное обучение. Предлагаемая технология зародилась и приобрела большую популярность в высших учебных заведениях и институтах повышения квалификации США, Германии, Англии и других стран. В настоящее время модульное обучение взято на вооружение многими образовательными организациями нашей страны.

     Но, несмотря на достаточную «зрелость» модульного обучения и в содержательном, и в «возрастном» аспекте (оно возникло в 60-е годы ХХ (20) века), существуют различные точки зрения на понимание модуля и технологии его построения как в плане структурирования содержания обучения, так и разработки форм и методов обучения. Ряд зарубежных авторов (В. Гольдшмидт, М. Гольдшмидт и др.) понимают под модулем формирование самостоятельно планируемой единицы учебной деятельности, помогающей достичь чётко определенных целей [67]. Несколько иначе определяет суть модуля Дж. Рассел, а именно, как построение автономных порций учебного материала [77, с. 5].

     Совершенно иное понимание модуля можно найти в работе А. А. Вербицкого. Он вводит понятие деятельностный модуль «в качестве единицы, задающей переход от профессиональной деятельности к учебной, от реальных задач и проблем к аудиторным» [12, с. 74]. Автор подчёркивает, что понятие «деятельностный модуль» принципиально отличается от понятия обучающий модуль, под которым понимается фрагмент содержания курса вместе с методическими материалами к нему». А. А. Вербицкий группирует деятельностные модули в следующие блоки: общеметодологический, конкретно-методологический, теоретический, практический и социальный, совокупность которых и составляет модель специалиста.

     Анализируя профессиональную подготовку кадров, Ю. К. Балашов и В. А. Рыжов отмечают следующие преимущества и особенности метода модульного обучения:

1) разбивка специальности на законченные части (модули и его элементы), имеющие самостоятельное значение;

2) отсеивание материала, являющегося «лишним» для данного конкретного вида работ;

3) максимальная индивидуализация продвижения в обучении [2, с. 97].

     Модуль, как отмечают авторы, представляет собой определенный объём учебной информации, необходимой для выполнения какой-либо конкретной деятельности. Он может включать несколько модульных единиц, каждая из которых содержит описание одной законченной операции или приёма. Модульные единицы могут расширять и дополнять содержание модуля в зависимости от требований конкретной деятельности.

     Модуль может быть представлен как учебный элемент в форме стандартизированного буклета, состоящего из следующих компонентов:

- точно сформулированная учебная цель;

- список необходимого оборудования, материалов и инструментов;

- список смежных учебных элементов;

- собственно учебный материал в виде краткого конкретного текста, сопровождаемого подробными иллюстрациями;

- практические занятия для обработки необходимых навыков, относящихся к данному учебному элементу;

- контрольная (проверочная) работа, которая строго соответствует целям, поставленным в данном учебном элементе.

     Компоненты учебного элемента не являются жёстко фиксированными и могут варьироваться в зависимости от конкретной дисциплины. Так, при разработке модулей по геометрии М. Ланге [70] основное внимание уделяет компактному расположению учебного материала с широким привлечением наглядности (рисунков, схем и чертежей), а также построению системы вопросов, упражнений и задач для обработки материала, представленного в учебном элементе.

     Метод модулей является одним из направлений индивидуализированного обучения, позволяющим осуществлять «самообучение с регулированием не только темпа работы, но и содержания учебного материала» [10, с. 87]. Метод модулей реализуется поэтапно. Сначала определяются учебные цели, затем проводится диагностический анализ и предварительная оценка способностей учащихся. На этой основе планируется последовательное расположение материалов учебно-познавательного курса по модулям и на заключительном этапе определяются критерии оценки достигнутых результатов [10].

     В школах уже несколько лет внедряется модульная система обучения, согласно которой весь цикл учебных предметов в школе разбивается на 2000 модулей трех типов: общие, специальные, интегративные. Каждый модуль имеет структуру, отражающую основные элементы; цель (общая или специальная); входной уровень, планируемые результаты обучения (знания, умения, элементы поведения), содержание (контекст, методы и формы обучения, процедуры оценки). Такая система предоставляет учащимся самостоятельный выбор индивидуального темпа продвижения по программе и саморегуляцию своих учебных достижений [72,73].

     В целом, по оценкам исследователей, модульное обучение позволяет сократить время учебного курса на 30% без ущерба для полноты изложения и глубины усвоения материала. Этот момент в модульном обучении созвучен фактору  «сжатия» в концепции инженерии знаний.

     Наиболее интенсивно модульное обучение стало внедряться в отечественную школу в 80-х годах ХХ (20) века. Учителя цель разработки модулей видят в следующем: «расчленение содержания каждой темы курса на составные компоненты в соответствии с профессиональными, педагогическими и дидактическими задачами, определение для всех компонентов целесообразных видов и форм обучения, согласование их по времени и интеграция в едином комплексе. Для достижения этой цели предлагается следующая структура модуля: наименование модуля; теоретические занятия; практические занятия; программное обеспечение; самостоятельная работа; результаты обучения (теоретические знания и практические навыки)» [13, с. 30,31].

     Обобщая исследования по модульному обучению, П. А. Юцявичене подчеркивает: «Сущность модульного обучения состоит в том, что обучающийся более самостоятельно или полностью самостоятельно может работать с предложенной ему индивидуальной учебной программой, содержащей в себе целевую программу действий, банк информации и методическое руководство по достижению поставленных дидактических целей. При этом функции педагога могут варьироваться от информационно-контролирующей до консультативно-координирующей. Инвариантными компонентами в структуре модуля выступают: учебный текст, руководство к обучению, консультация педагога. Для облегчения ориентации учащихся в модуле предлагается ряд символических обозначений, указывающих дидактическую цель, наиболее важные фрагменты текста, контрольные вопросы и т. д.» [59].

     Одним из главных элементов модульного обучения является система контроля и оценки достижений учащихся. Одной из форм такой системы является индивидуальный коммуникативный индекс (рейтинг}, который нацеливает учащегося на получение максимального количества баллов при изучении модуля. Процент распределения баллов среди различных видов контроля следующий: текущий контроль даёт до 30-35% общей максимальной оценки, промежуточный - 20-25%, практические занятия и курсовая работа до 25%, доля баллов, полученных на экзамене, - около 20%. Такая система стимулирует повседневную систематическую работу, значительно повышает состязательность в учёбе [43].

     На современном этапе развития науки понятие модульности приобретает методологический смысл. Модульность выступает как один из основных принципов системного подхода. Принцип модульности, наряду с таким важным принципом системного подхода, как принцип развития, определяет динамичность и мобильность функционирования системы. Причём сама система может быть представлена как совокупность модулей или рассматриваться как отдельный модуль в структуре более общей системы. Традиционное, чисто техническое представление о модуле, как о фиксированном функциональном узле, на наш взгляд, страдает определённой незавершенностью. Это особенно заметно в свете современных представлений о системном анализе, согласно которым система может содержать как базовые, так и вариативные модули, а модуль, в свою очередь, иметь базовый и вариативный компоненты. Такое строение модуля придает ему качества мобильности и гибкости. А использование принципа модульности в процессе обучения способствует формированию мобильности знаний и гибкости метода, что является неотъемлемой частью компетентности. Кроме того, такое понимание модульности в обучении предупреждает игнорирование логики учебного предмета. Сохранению логики учебной дисциплины способствует наличие базовых и вариативных модулей, а также соответствующих компонентов в структуре отдельного модуля.

     Схематически модуль представляет собой целостную совокупность элементов системы, имеющую связи (входы и выходы) как с другими элементами системы, так и с элементами «не-системы» (рис. 3).

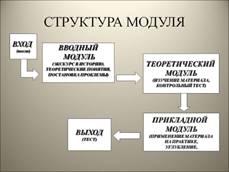
Рис. 3. Структура модуля

     Связи данного модуля с другими модулями могут быть как моновалентными, так и поливалентными (рис. 4).

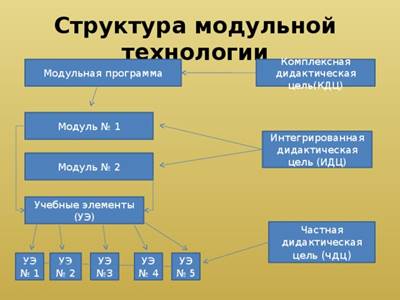
Рис. 4. Структура модульной технологии

     Поливалентный модуль M1 связан с двумя моновалентными модулями М2 и М3, один из которых, например М3, может быть базовым, а другой - М2 - вариативным. Модуль М3, в свою очередь, связан с модулем М 4, который содержит базовый (внутренний квадрат) и вариативный (внешний квадрат) компоненты [35].

     Проблемное обучение. Общеизвестно влияние проблемного обучения на активизацию мыслительной деятельности обучаемых, на формирование, развитие нестандартных подходов к решению проблем и, наконец, на развитие творческого мышления. Это влияние обеспечивается созданием в процессе обучения специальных ситуаций интеллектуального затруднения - проблемных ситуаций и их разрешения. Проблемная ситуация служит не только источником интеллектуального затруднения, что является необходимым условием развития мышления обучающихся, но и важным мотивационным, а вместе с тем и эмоциональным средством в процессе обучения. Эффективность проблемного обучения убедительно доказана как в работах отечественных (А. М. Матюшкин, М. И. Махмутов и др.) и зарубежных (Дж. Дьюи, Э. де Боно, В. Оконь и др.) учёных, так и непосредственно на практике при обучении различным дисциплинам в разных типах школ: начальной, средней специальной и высшей.

     Несмотря на то что исследования в области проблемного обучения ведутся уже сравнительно давно, что позволяет некоторым учёным уже подводить какие-то итоги [69], тем не менее, проблемное обучение привлекает к себе пристальное внимание учёных и на современном этапе [22, 78]. Возникает ощущение, что после некоторого затишья начинается новая волна исследований этой, несомненно, интересной области дидактики. Новые проблемы возникают в связи с использованием достижений теории искусственного интеллекта в обучении [76], индивидуализацией в проблемном обучении, применением различных форм (группового, кооперативного) обучения [75], использованием компьютерной техники в проблемном обучении.

     В технологии проблемно-модульного обучения основное внимание мы уделяем такому малоисследованному аспекту проблемного обучения, как формирование критического мышления учащихся. Однако при этом мы не претендуем на целевую установку – «развитие творческого мышления учащихся», ибо эта цель труднодостижима в реальных условиях процесса обучения в школе и ограничиваемся попыткой формирования критического мышления обучающихся, что, на наш взгляд, является первым шагом к творчеству.

     Критическое мышление, наряду с мобильностью знания и гибкостью метода, служит составным элементом компетентности специалиста. Критичность предполагает умение действовать в условиях выбоpa и принятия альтернативных решений, умение опровергать заведомо ложные решения, наконец, умение просто сомневаться. Формирование и развитие критичности в процессе проблемно-модульного обучения мы осуществляем, через целенаправленное создание специальных ситуаций – ситуаций на поиск ошибок. На этой идее построен метод опоры на ошибки. В процессе реализации этого метода используются три основные группы ошибок: гносеологические, методические и учебные.

     Гносеологические ошибки - ошибки познавательного характера, совершенные в процессе эволюции знания. Они объективно обусловлены относительностью нашего знания: его неполнотой и ограниченностью. Использование гносеологических ошибок в процессе обучения формирует, развивает у обучающихся умение критически осмысливать действительность, анализировать и исправлять ошибки, а также существенно меняет их отношение к учебному предмету и науке: содержание изучаемой дисциплины предстает перед учащимися не как набор готовых истин, а как историческая драма идей и людей, как борьба научных школ и направлений, как противостояние инерции и обновления. Особый интерес среди гносеологических ошибок вызывают ошибки, «допущенные"» известными учёными. Это так называемые «великие» ошибки. Луи де Бройль, видный физик, считал весьма полезным поразмыслить над ошибками, допущенными великими умами, поскольку они часто имели серьезное основание для того, чтобы их сделать.

     Методические ошибки - ошибки преподавания, которые заключаются в нарушении педагогом психолого-педагогических закономерностей восприятия, памяти, мышления в процессе обучения. Методические ошибки тесно связаны с учебными ошибками. Чаще всего ошибки учения - результат ошибок преподавания.

     Учебные ошибки сгруппированы в специальные таблицы по каждому проблемному модулю и используются в дальнейшем в качестве одного из средств обучения. Иными словами, в проблемно-модульном обучении зона ближайшего развития учащегося расширяется до области критических ситуаций - области ошибок, к которым приводит поверхностное усвоение и неправильное применение нового знания. При таком условии область перехода от незнания к знанию перестает быть для учащихся основной проблемой, она становится естественным звеном, зоной его актуального развития.

     Подвергнув тщательному анализу преимущества и недостатки различных подходов к проблемному и модульному обучению, а также принимая во внимание достоинства теорий «сжатия» учебной информации, мы пришли к выводу, что наиболее целесообразной для формирования, развития компетентного специалиста технологией является проблемно-модульное обучение.

     Эффективность процесса обучения трудно обеспечить классическими или отдельными новыми методами. Необходима взаимосвязь различных методов обучения, их взаимодополнение и взаимоусиление. Иными словами, современный этап развития дидактики наряду с разработкой новых технологий обучения требует их интеграции с уже известными, что позволяет создавать «полифонические» дидактические системы. Преимущество таких систем перед «монофоническими» заключается в том, что они аккумулируют достоинства интегрируемых теорий и образуют целостность, позволяющую выходить на новый качественный уровень решения педагогических задач.

     Именно поэтому, приняв целевую установку на формирование и развитие общеобразовательной компетентности, мы предприняли попытку смоделировать технологию проблемно-модульного обучения в школе, интегрирующую достижения теории проблемного обучения, концепции «сжатия» знаний и обучения в условиях взаимосвязи общего и профессионального образования.

     Перестройка процесса обучения на проблемно-модульной основе позволяет:

1) интегрировать и дифференцировать содержание обучения путём группировки проблемных модулей учебного материала, обеспечивающих разработку курса в полном, сокращённом и углублённом вариантах;

2) осуществлять самостоятельный выбор учащимися того или иного варианта курса в зависимости от уровня облученности и обеспечивать индивидуальный темп продвижения по программе;

3) использовать проблемные модули в качестве сценариев для создания педагогических программных средств;

4) акцентировать работу преподавателя на консультативно-координирующие функции управления познавательной деятельностью учащихся;

5) сократить курс обучения без особого ущерба для полноты изложения и глубины усвоения учебного материала на основе адекватного комплекса методов и форм обучения.

     Наряду с перечисленным, специфику проблемно-модульной технологии обучения отражают следующие основные принципы её построения:

1) системное квантование;

2) мотивация;

3) проблемность;

4) модульность;

5) когнитивная визуализация;

6) опора на ошибки;

7) экономия учебного времени.

     Рассмотрим содержание каждого из названных выше принципов.

     Принцип системного квантования вытекает из требований теорий сжатия учебной информации, к которым можно отнести элементы содержательного обобщения (В. В. Давыдов), теорию укрупнения дидактических единиц

(П.М. Эрдниёв) концепцию инженерии знаний (Д. А. Поспелов и др.). Кроме того, этот принцип предполагает учёт следующих психолого-педагогических закономерностей:

1) учебный материал большого объема запоминается с трудом;

2) учебный материал, компактно расположенный в определенной системе, облегчает восприятие;

3) выделение в изучаемом материале смысловых опорных пунктов способствует эффективности его запоминания.

     При этом следует подчеркнуть, что требования этих закономерностей не должны идти вразрез с принципами научности и фундаментальности и тем самым нарушать логику учебного предмета. Принцип системного квантования обеспечивается соответствующим структурированием учебной информации в проблемном модуле.

     Общая структура проблемного модуля представлена на рис. 5.

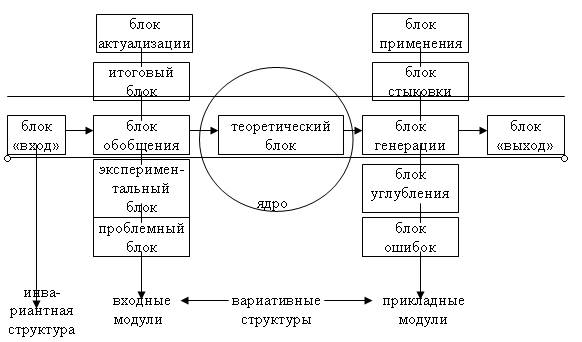
Рис. 5. Общая структура проблемного модуля

     Основной дидактической функцией блока «вход» является осуществление актуализирующего контроля. Главная особенность этого контроля заключается не только в том, что его прохождение означает своего рода выдачу «пропуска» в проблемный модуль, но прежде всего в том, что тестовые задания предполагают актуализацию тех опорных знания и способов действий, которые необходимы для усвоения содержания всего проблемного модуля. Наряду с этим актуализирующий контрольный тест снабжен соответствующим указателем, отсылающим учащегося к тому учебному материалу, знание которого нужно для успешного выполнения данного теста. В тех же случаях, когда обращение к учебному материалу не дает должного эффекта, учащийся может получить консультацию у преподавателя. Такая компоновка входного блока соответствует структуре контролирующей учебной программы.

     Принцип проблемности отражает требования психолого-педагогической закономерности, согласно которой введение таких стимулирующих звеньев, как проблемная ситуация и практическая направленность повышают эффективность усвоения учебного материала. Этот принцип реализуется постановкой и решением укрупнённых проблем, а также служит исходным положением для конструирования проблемного модуля и его элементов, в частности для учебных элементов теоретического блока проблемного модуля. Требования принципа проблемности отражаются в проблемном блоке при постановке проблемы и выдвижения гипотез, в теоретическом блоке - при обосновании выдвинутых гипотез и в блоке стыковки - при решении проблемы и проверке её решения.

     Принцип когнитивной визуализации вытекает из психолого-педагогической закономерности, согласно которой эффективность усвоения повышается, если наглядность в обучении выполняет не только иллюстративную, но и когнитивную функцию. Именно поэтому составными компонентами проблемного модуля являются когнитивно-графические учебные элементы (блок-рисунки), выполненные в цвете. Выбор рисунка в качестве главного элемента проблемного модуля далеко не случаен. В первую очередь он положительно влияет на развитие зрительной памяти и пространственного мышления учащихся. Тем самым блок-рисунок помогает подключить к процессу усвоения учебного материала богатый потенциал образного правого полушария мозга, которого так не хватает при традиционном «левополушарном» обучении. Далее, блок-рисунок, компактно иллюстрирующий содержание учебного материала, способствует формированию и развитию у учащихся системности знаний. Немаловажное значение имеет его цветовое представление. Помимо того, что блок-рисунок, выполненный в цвете, служит одним из средств эстетического воспитания учащихся, он выгодно отличается от черно-белого блок-рисунка. Опыт применения блок-рисунка свидетельствует о следующей устойчивой зависимости: эффективность восприятия и запоминания учебной информации попытается, если блок-рисунок представлен в цвете.

     Принцип опоры на ошибки направлен на систематическое создание в процессе обучения ситуаций на поиск ошибок. Требования этого принципа находят отражение в историческом блоке и блоке ошибок. Этот принцип направлен также на разработку дидактических материалов и средств, ориентированных на формирование аппарата предвосхищения (акцептора результатов действия) в структуре функциональной системы психической деятельности обучаемых. Немаловажная роль принципа опоры на ошибки заключается в ориентации обучения на формирование и развитие критичности мышления - составного компонента общеобразовательной компетентности.

     Принцип экономии учебного времени направлен на обеспечение резерва времени для индивидуальной и групповой самостоятельной работы учащихся. Согласно исследованиям в области проблемно-модульного обучения, оно приносит до 30% экономии учебного времени без ущерба для глубины и полноты изучения материала.

     Педагогическая технология проблемно-модульного обучения имеет свои преимущества и недостатки. При наличии определённых условий реализация этой технологии даёт самые эффективные результаты, в других же условиях она может быть малоэффективной и её целесообразно заменить другой технологией. Вопросы взаимосвязи данной технологии с другими, выработки критериев отбора технологии обучения являются на сегодняшний день одними из сложнейших проблем.

     Попытаемся дать некоторые ориентиры, представляющиеся, на наш взгляд, важными при решении вопросов взаимосвязи проблемно-модульного обучения с другими технологиями. Для этого, прежде всего, следует выделить преимущества и недостатки данной технологии.

     К преимуществам проблемно-модульного обучения относятся:

- направленность на формирование мобильности знаний, гибкости метода и критичности мышления обучаемых;

- вариативность структуры проблемного модуля;

- дифференциация содержания учебного материала;

- обеспечение индивидуализации учебной деятельности;

- разнообразие форм и методов обучения;

- сокращение учебного времени без ущерба для глубины и полноты знаний учащихся;

- эффективная система рейтингового контроля н оценки усвоения знаний учащимися.

     Среди недостатков проблемно-модульного обучения можно выделить:

- «фрагментарность» обучения, под которым понимается большой удельный вес самостоятельной работы учащихся вплоть до «самообучения», что можно расценивать как «предоставленность учащихся самим себе» и отсутствие полноценного процесса обучения;

- игнорирование целостности и логики учебного предмета;

- сужение подготовки учащихся; сокращение курса обучения до серии дискретных и несвязных проблем или задач, формирование лишь частных, конкретных умений в ущерб обобщённым;

- трудоёмкость изготовления проблемных модулей.

     Многие из перечисленных недостатков, наиболее явно проявлявшиеся на этане, становления технологии проблемно-модульного обучения, постепенно «сглаживаются» [72, 73]. Это особенно относится к сохранению целостности и логики учебного предмета, формированию, развитию системности знаний и обобщённых умений учащихся. Отчасти это достигается тем, что в процессе реализации проблемно-модульного обучения используются преимущества других технологий. Более того, реализовать ту или иную технологию «в чистом виде» практически невозможно. Так или иначе, приходится опираться на уже устоявшиеся дидактические структуры и традиционные подходы к организации учебного процесса. Идея новой технологии проявляется, как правило, в одном или нескольких «ведущих» моментах, в то время как большинство «фоновых» характеристик процесса обучения может быть традиционным.

     Таким образом, один из тривиальных путей взаимосвязи технологии проблемно-модульного обучения с другими технологиями заключается в поиске таких дидактических элементов, которые, не нарушая главной идеи технологии, помогали бы нивелировать её недостатки.

     Выбор технологии связан с анализом следующих критериев: целевой ориентации; содержательной специфики; трудоёмкости; индивидуализации обучения; критерия времени и критерия технической оснащённости.

     Критерий целевой ориентации предполагает учёт психолого-педагогической направленности технологии. Так, например, если ведущая цель заключается в развитии памяти обучающихся, то целесообразно применять интенсивные современные технологии обучения с элементами гипнопедии, суггестокибернетики и т. д. Общеизвестны высокие результаты по развитию памяти (в частности, словарного запаса) учащихся при изучении иностранных языков с помощью интенсивных технологий.

     Если же ведущая цель состоит в развитии мышления учеников, то могут быть использованы технологии проблемного обучения с широким привлечением методов коллективной интеллектуальной и деятельности, («мозгового штурма», синектики, морфологического анализа и т. д.).

     Критерий содержательной специфики в той или иной степени связан с предыдущим критерием и требует учёта особенностей дисциплины, в процессе преподавания которой планируется реализация выбираемой технологии. Так, специфика содержания естественно-математических дисциплин диктует выбор технологий проблемного или задачного обучения (обучение через задачи). В истории методики преподавания математики известны такие методы обучения, как метод целесообразных задач, метод сквозных задач и другие, которые могут быть включены в технологию проблемно-модульного обучения. В обучении гуманитарным предметам могут быть использованы, например, технологии диалогового обучения (школа диалога культур и т. д.).

     В недрах профессионального обучения зародилась технология проблемно- модульного обучения. Однако это не означает строгой «безоговорочной» привязанности технологий к содержанию предмета. Могут быть переносы и взаимодействие технологий в рамках одной дисциплины. Именно такой вариант взаимодействия технологий (проблемная + модульная) применён нами при обучении математике в школе.

     Критерий трудоёмкости реализации технологий включает учет энергозатрат педагогического труда преподавателя, его методического «вкуса» и возможностей. Это обусловлено в какой-то мере разнообразием технологий. Одни технологии требуют большой подготовительной работы (разработка дидактических материалов, составление, текстов контрольных и самостоятельных работ), что облегчает непосредственное проведение учебного занятия и ограничивает деятельность педагога осуществлением консультативно-корректирующих функций. К таким технологиям относятся, как правило, информационные технологии, в которых подавляющую часть учебного времени учащиеся заняты диалогом с компьютером. Функции учителя в этом случае, заключаются в подготовке соответствующих программных средств, консультировании и коррекции познавательной деятельности учащихся.

     В других технологиях (например, диалогового характера) преподаватель все время находится во взаимодействии с учащимися, организуя беседы, дискуссии и т. д., что требует выполнения более сложных по трудоёмкости педагогических функций непосредственно в учебном процессе, нежели коррекция и консультация. Кроме того, у разных преподавателей свои методические «вкусы». У кого-то хорошо развиты коммуникативные способности, богатая и образная речь - в этом случае предпочтительнее выбор диалоговых технологий, а также технологий, в которых большой удельный вес игровых методов. У других педагогов преобладает склонность к наглядному обучению, наиболее развиты изобразительные способности - здесь лучше остановить выбор на технологиях визуализации обучения. Естественно, что могут быть сочетания «вкусов» и соответствующая интеграция технологий. Единственное, чего не должно быть - это методической «безвкусицы».

     Следующий критерий - критерий индивидуализации - связан с оптимальным сочетанием индивидуальных, парных, групповых, коллективных форм организации обучения. Известно, что некоторые технологии (назовем их образно «репетиторскими») наиболее результативны ори обучении в малых группах или индивидуально. Другие же технологии, направленные, например, на развитие коммуникативных способностей, эффективны только в условиях коллективных форм организации обучения.

     Критерий времени предполагает учёт временных затрат для достижения планируемых результатов обучения. Соответственно технологии могут быть интенсивными, обычными и экстенсивными. Если необходимо обеспечить «форсированную» краткосрочную подготовку обучающихся, то вполне естественно выбрать интенсивную технологию, но учитывая при этом её трудоёмкость. В условиях, когда временные рамки не столь жестки, можно использовать обычные технологии. Вместе с тем имеются экстенсивные технологии, сторонники которых считают наличие достаточно большого количества времени важным фактором успешного, результативного обучения [62]. Это свидетельствует о том, что учёт временного критерия является необходимым условием выбора технологии обучения.

     Критерий технической оснащенности непосредственным образом связан с материально-технической базой педагогической технологии. Естественно, что реализация компьютерной технологии возможна только лишь при наличии компьютеризованных аудиторий; аналогично обстоит дело и с любой другой технологией. Образно говоря, нельзя выбирать телекоммуникационную технологию обучения, имея в распоряжении лишь только «доску и мел». Новые информационные технологии связаны с огромными экономическими затратами, поэтому учёт этого фактора при выборе технологии очевиден.

     Развитие современной педагогики ориентируется на проектирование «гибких» педагогических технологий. «Гибкость» в педагогике проявляется в переходе от единой школы к многообразию их новых типов (гимназий, лицеев, колледжей), от использования единых учебников - к выбору альтернативных учебников и учебных пособий, от единых программ и учебных планов - к их варьированию посредством выделения базовых (обязательных) предметов и предметов по выбору, от преимущественно коллективных форм организации обучения – к индивидуальным формам и обучению в малых группах, от единого уровня общеобразовательной подготовки к диалектически взаимосвязанной интеграции и дифференциации содержания обучения, от застывшей формы обучения - урока - к многообразию форм обучения, от традиционных методик обучения — к их полифоническому разнообразию и т. д. Комплексное решение этих вопросов- актуальнейшая проблема современной педагогики.

     Не претендуя на целостное решение этой проблемы, мы сосредоточили свои усилия на одном из вариантов проектирования «гибкой» технологии обучения, базирующейся на проблемно-модульном подходе. По нашему мнению, данный подход обладает широкими возможностями и богатым потенциалом в обеспечении, именно гибкости процесса обучения. Потенциал предлагаемой нами технологии проблемно-модульного обучения заложен в теоретических концепциях, составляющих методологическую основу технологии.

     В первую очередь, это общая теория функциональных систем и ведущие её принципы: системного квантования, модульности и проблемности. Во-вторых, – это интеграция дидактически адаптированных теорий, вытекающих из перечисленных принципов: теории «сжатия» знаний, теории проблемного и модульного обучения. Целостным качеством, возникающим в результате интеграции этих теорий, и является гибкость, а технология, сконструированная на основе данной интеграция, получила название гибкой технологии проблемно-модульного обучения.

     В процессе изложения основных особенностей предлагаемой технологии мы попытались ответить на следующие важные вопросы:

Ø    Как отбирать и структурировать содержание учебного материала?

Ø    Как выделять базовый необходимый минимум знаний и умений учащихся?

Ø    Что ставить во главу угла: описательные знания (информацию) или познавательные методы (инструмент для получения информации и её переработки)?

Ø    Как обеспечить уровневую и профильную дифференциацию обучения?

Ø    Как наглядно и компактно конструировать учебные элементы и дидактические материалы?

Ø    Как выбирать и сочетать целесообразные методы и формы обучения?

Ø    Как стимулировать учебно-познавательную деятельность учащихся при помощи рейтинговой системы контроля и оценки?

     Одним словом, на протяжении всего изложения мы постоянно держали в поле зрения самый главный вопрос любой технологии обучения: «Как учить результативно?»

Литература

1. Анохин П. К. Принципиальные вопросы общей теории функциональных систем // Принципы системной организации функций. — М., 1973. - С. 5-61.

2. Балашов Ю. К., Рыжов В. А. Профессиональная подготовка кадров в условиях капитализма. - М.: Высшая школа, 1987.

3. Балк М. Б., Балк Г. Д. О привитии школьникам навыков эвристического мышления // Математика в школе. - 1985. - № 2. -С. 55-60.

4. Башмаков М. И. Математика. - М.: Высшая школа, 1987.

5. Бескин Н.М. Методика геометрии. - М.; Л.: Учпедгиз, 1947.

6. Беспалько В. П. Слагаемые педагогической технологии. -М.: Педагогика, 1989.

7. Боголюбов В. И. Педагогическая технология: эволюция понятия // Сов. педагогика. - 1991. - № 9. - С. 123-128.

8. Б р а д и с В. М. Методика преподавания математики в средней школе. - М.: Учпедгиз, 1954.

9.Буш Г. Я. Основы эвристики для изобретателей. - Рига, 1977.

10. Васильева Т. В. Модули для самообучения // Вестник высшей 'школы. - 1988. - № 6. - С. 86-87.

11. Вевдровская Р. Б. Очерки истории советской дидактики. -— М.: Педагогика, 1982.

12.Вербицкий А. А. Активное обучение в высшей школе: контекстный подход. - М.: Высшая школа, 1991.

13. Гареев В. М. и др. Принципы модульного обучения // Вестник высшей школы. - 1987. - № 8.

14. Германович П. Математика в школах профотбора // Просвещение на транспорте. - 1927.-№ 7-8.

15. Гнеденко Б. В., Черкасов Р. С. О курсе математики в школах Японии // Математика в школе. - 1988. - № 5.

16. Грегори Р. Л. Разумный глаз. - М.: Мир, 1972.

17. Давыдов В. В. Проблемы развивающего обучения. - М.: Педагогика, 1986.

18.3арецкий М. И. За качество урока в школе ФЗУ // За промышленные кадры. - 1933. - № 12. 19. Зенкин А. А. Когнитивная компьютерная графика. - М.: Наука, 1991.

20. Кандрашина Е. Ю. и др. Представление знаний о времени и " пространстве в интеллектуальных системах / Под ред. Д. А. Поспелова - M.: Мир, 1989.

21. Кларин М. В. Педагогическая технология в учебном процессе: Анализ зарубежного опыта. - М.: Знание, 1989.

22. Кудрявцев В. Т. Проблемное обучение: истоки, сущность, перспективы. - М.: Знание, 1991.

23. Ландшеер В. Концепция "минимальной компетентности" // Перспективы: вопросы образования. - 1988. - № 1.

24. Ланков А. В. Математика в трудовой школе: Очерки по методике математики. - М.: Работник просвещения, 1924.

25. Лебединцев К. Ф. Введение в современную методику математики. - Киев: Гос. изд-во Украины, 1925.

26. Лобачевский Н. И. Научно-педагогическое наследие... / Отв. ред. П. С. Александров и Б. Л. Лаптев. - М.: Наука, 1976.

27. Марев И. Методологические основы дидактики. - М.: Педагогика, 1987.

28. Махмутов М. И. Проблемное обучение: Основные вопросы теории. - М.: Педагогика, 1975.

29. М а х м у т о в М. И. Современный урок. - М.: Педагогика, 1985.

30. Метельский Н. В. Психолого-педагогические основы дидактики математики. - Минск: Высшая школа, 1977.

31. Методика преподавания математики в средней школе: Общая методика / Сост. Р. С. Черкасов, А. А. Столяр. - Ml: Просвещение,

32. Минский М. Фреймы для представления знаний. - М.: Энергия,

33. Моделирование педагогических ситуаций / Под ред. Ю. Н. Кулюткина, Г. С. Сухобской. - М.: Педагогика, 1981.

34. Моро М. И., Пышкало A.M. О. совершенствовании методов обучения математике // О совершенствовании методов обучения математике. - М.: Просвещение, 1978. - С. 7-51.

35. Оконь В. Введение в общую дидактику. - М.: Высшая школа, 1990.

36. Петрусинский В. В. Автоматизированные системы интенсивного обучения. - М.: Высшая школа, 1987.

37. Пойа Д. Математическое открытие. - М.: Наука, 1976.

38. Пойа Д. Математика и правдоподобные рассуждения. — М.: Наука, 1975.

39. Приобретение знаний / Пер. с япон. / Под ред. С. Осуги, Ю. Саэки. - М.: Мир, 1990.

40. Представление и использование знаний / Пер. с япон. / Под ред. X. Уэно. - М.: Мир, 1989.

41. Программа-минимум единой трудовой школы. Вторая ступень. - Л., 1925.

42. Рабочая книга по математике: Пособие для изучения математики по лабораторному плану и по аккордной системе / Под ред. Г. А. Понперека. - Ч. 1-3. - М.: Госиздат, 1923.

43. Рогинский В. М. Азбука педагогического труда. - М.: Высшая школа, 1990.

44. Рыбаков А. Система проектов в школе ФЗУ // Жизнь рабочей Школы. - 1930. - № 1. - С. 30-35.

45. Сагалович Г. Математика в комплексной системе преподавания в школе первого концерта. - Минск, 1928.

46. Салмина Н. Г. Знак и символ в обучении. - М.: Изд-во МГУ, 1989.

47. Системный анализ процесса мышления / Под ред. К. Д. Судакова. - М.: Медицина, 1989.

48. Третьяков М. Иллюстрированныйметод на уроках математики //Жизнь рабочей школы. - 1929. - № 5. - С. 41-48.

49. Ф о р м ы и методы общеобразовательной подготовки / Под ред. М. И. Махмутова. - М.: Педагогика, 1986.

50. Хамблин Д. Формирование учебных навыков. - М.: Педагогика, 1986.

51. Цирюльников А. Чему учиться: Заметки на полях истории педагогики // Учительская газ. - 1988. - 19,20,21 апр.

52. Чередов И. М. Формы учебной работы в средней школе: Кн. для учителя. - М.: просвещение, 1988.

53. Черкасов Р. С, Отани М. Новая программа по математике в школах Японии // Математика в школе. - 1991. - № 1. - С. 73-75.

54. Шатихвв Л.Г. Структурные матрицы и их применение для исследования систем, - М.: Машиностроение, 1991.

55.Шохор-Троицкий СИ. Геометрия на задачах: (Основной курс). - М.: Изд-во т-ва И. Д. Сытина, 1913.

56. Эйнштейн А. Физика, и реальность. - М.: Наука, 1965.

57. Эделмак Дж., Маунткастл В. Разумный мозг. - М.: Мир, 1981.

58. Эрдниев П. М. Системность знаний и укрупнение дидактической единицы // Сов. педагогика. - 1975. - № 4. - С. 72-80.

59. Юцявичене П. А. Теория и практика модульного обучения. Каунас: Швиеса, 1989.

60. Ястребинецкий Г. А., Блох А. Я. О математическом образовании в средних школах США. // Математика в школе. - 1988. - J* 4. - С. 73-76.

61. Вi11stein R., Lott T. Mathematics for Liberal arts: A problem solving approach. - Menlo Park: Benjamin Cummings, 1986.

62. Вlаnк W. Е. Handbook for developing Competency-Based Training Programs. - New-Jersey: Prentice Hall, 1982.

63. Bloom B. S., Broder L. Problem solving processes of college students. Supplementary Education Monograph. - Chicago: University of Chicago Press, 1950.

64. Bransford J. D., Stein S. B. The IDEAL problem solver.-" N-Y.: W.H. Freeman & C, 1984. -U .

65. Вгite11 Т. К. Competency and Exellence Minimum Competency Achivment Testing/Taeger R. M. & Title C.K. (eds). - Berkeley, 1980. -P. 23-29.

66. Сuгсh C. Modular courses in British higher education // A critical yassesment in higher education bulletin. - 1975, Vol. 3. - P. 65-84.

67. Goldschmidt В., Goldschmidt M. Modular Instruction in Higher Education // Higher Education. - 1972. - № 2. - P. 15-32.

68.International Annual on educational technology. - London, 1978-1979.

69. Кilpatriс Т. A retrospective account of the past twenty-five years of research on teaching mathematical problem solving // Teaching and Learning Mathematical Problem Solving: Multiple research perspectives. -London: LEA, 1985. - P. 1-16.

70. Lange V. Geometry in modules: Teacher's Manual. - London: Addison-Wesley P. C, 1986.

71. MadiganS., Rоuse M. Picture memory and visual-generation processes//The American Journal of Psychology.-1974, Vol. 87.-P. 151-158.

72. Modularization and progression: Issues in the 14-19 curriculum: Working Paper. - London: London Univ. Press. - 1989. - № 6.

73. Modularization and the new curricular. - London: FESC Report, 1986; Vol. 19. - № 4.

74. Moon B. Introducing the modular curriculum // The modular curriculum. - London, 1988. - P. 9-21.

75. Noddings N. Small groups as a setting for research on mathematical problem solving // Teaching and Learning Mathematical problem solving. -London; 1985. - P. 345-360.

76. Riss1and E. L. Artificial intelligence and the learning of mathematics: A tutorial sampling // Teaching and Learning Mathematical-problem solving. - London, 1985. - P. 147-176.

77. Russell J. D. Modular Instruction // A Guide to the Design, Selection, Utilization and Evaluation of Modular Materials. - Minneapolis; BPC, 1974.

78. Sсhoenfeld A. H. Mathematical problem solving. - London: Academic Press, 1985.

79.Watkins P. Modular approaches to the secondary curriculum // SCDC. - London, 1986. - P. 12-18.

86. Барабан М.А. О проведении уроков "Анализ контрольной работы" // Математика в школе. - 1988. - № 3. - С. 24-25.

81. Башмаков М.И., Резник Н.А. Развитие визуального мышления на уроках математики // Математика в школе. - 1991. -М 1. - С 4-8.

82. Векслер С. И. Найтии преодолеть ошибку // Математика в школе. - 1989. - № 5. - С. 40-42.

83. Вивюрский В.Я. Обнаружение и исправление ошибок по химии//Сред. спец. образование. - 1989. - № 1. - С. 22-23.

84. 3ив Б . Г. Быстротечные минуты урока // Математика в школе. - 1988. - № 3. - С. 13-17.

85. Методика блочно-модульного обучения / Под ред. О.Е. Лисейчикова и М.А. Чошанова. - Краснодар: Сов. Кубань, 1989. - 123 с.

86. Тетерина Д. Д. Модульная система изучения органической химии//Специалист. - 1992. -№ 3. - С. 5-6.

87. Урок физики в современной школе: Творческий поиск учителей / Сост. Э.М. Браверман. Под ред. В.Г. Разумовского. - М.: Просвещение, 1993.- 288 с

88. Эрдниев П.М. Укрупнение дидактических единиц как технология обучения. - Ч. 1. - М.: Просвещение, 1992. - 175 с.