
Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа №1
имени Чернявского Якова Михайловича
станицы Крыловской муниципального образования Крыловский район
Исследовательский проект на тему
«Применение формулы Пика в геометрии»
Выполнила:
Крамаренко Виктория,
обучающаяся 9«А» класса
Руководитель:
Газман Татьяна Николаевна,
учитель математики
Крыловская, 2024 г
Введение........................................................................................................................... 2
Основная часть................................................................................................................. 4
1. Теоретическая часть......................................................................................................... 4
1.1. Историческая справка...................................................................................................... 4
1.2. Доказательство формулы Пика....................................................................................... 5
2. Практическая часть............................................................................................................. 6
2.1. Нахождение площади фигур геометрическим методом и по формуле Пика........... 6
2.2. Практическое применение формулы Пика. Применение формулы Пика для нахождения площади поверхности детали……………………………………………… .9 Заключение ..13
Список литературы............................................................................................................... 15
Приложение........................................................................................................................... 16
Введение
Актуальность темы моей работы определяется тем, что в настоящее время в заданиях открытого банка данных к ОГЭ и ЕГЭ по математике в первой части встречаются задачи на вычисление площади фигуры, изображённой на клетчатой бумаге. Чтобы вычислить площадь изображённой фигуры, необходимо сделать дополнительные построения: разбить данную фигуру на несколько треугольников и прямоугольник, провести высоту в треугольнике. Решая подобные задачи, у меня возникли вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на вычисление площади фигур, изображённых клетчатой бумаге. Если есть вопрос, надо на него постараться найти ответ. Я приступила к изучению литературы, Интернет-ресурсов по данной теме и выяснила, что есть специальная формула для решения этих задач. Эта формула Пика. Она меня заинтересовала, и я попробовала решать задания, используя данную формулу. Задачи решались очень быстро и легко. Исследуя литературу, мне встретились задачи с практическим содержанием на нахождение площади земельных участков. Я решила проверить, применима ли данная формула для нахождения площади территории школы, микрорайонов города, области. А так же рационально ли ее
применение для решения задач.
Цель работы: обосновать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.
1) Изучить литературу по данной теме.
2) Рассмотреть геометрические способы решения задачи на нахождение площади фигур, изображённых на клетчатой бумаге. Рассмотреть способ решения задачи на нахождение площади фигур, используя формулу Пика.
4) Сравнить и проанализировать результаты исследования.
В связи с этим возникла гипотеза о том, что задачи на нахождение площади фигур, изображённых на клетчатой бумаге, можно решить с помощью формулы Пика более рационально.
Объект исследования: формула Пика.
Предмет исследования: применение формулы Пика при решении задач, на нахождение площади фигур, изображённых на клетчатой бумаге.
Методы исследования: моделирование, анализ, сравнение, обобщение.
Теоретическое обоснование: вопрос расчета площадей многоугольников на клетчатой бумаге занимал многих математиков. В 1899 году формула расчета по узлам была открыта польским математиком Георгом Пика. В 1949 году польский математик Гуго Штейнгауз формулу Пика опубликовал В своей книге «Математический калейдоскоп». Л. В. Горина, кандидат педагогических наук, в «Материалах для самообразования учащихся» так описывала данную формулу: «Ознакомление с формулой Пика особенно актуально накануне сдачи ЕГЭ и ГИА. С помощью этой формулы можно без проблем решать большой класс задач, предлагаемых на экзаменах, — это задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге. Маленькая формула Пика заменит целый комплект формул, необходимых для решения таких задач. Формула Пика будет работать «одна за всех…»!».
1. Теоретическая часть
1.1. Историческая справка
Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Уже эта простая решетка послужила К. Гауссу отправной точкой для сравнения площади круга с числом точек с целыми координатами, находящихся внутри него. То, что некоторые простые геометрические утверждения о фигурах на плоскости имеют глубокие следствия в арифметических исследованиях, было в явном виде замечено Г. Минковским в 1896 г., когда он впервые для рассмотрения теоретико- числовых проблем привлек геометрические методы. Нарисуем на клетчатой бумаге какой-нибудь многоугольник. Попробуем теперь рассчитать его площадь. Как это сделать?
1 способ Подсчет клеток
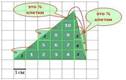 |
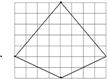 |
Рис.2 Разбиение на простые фигуры 3 способ: Вписывание в прямоугольник и вычитание «лишнего»
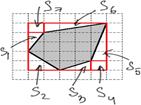
Рис.3 Вписывание в прямоугольник
Использованные нами способы не сложные, но иногда очень громоздкие, кроме того они годятся не для всяких многоугольников. Так многоугольник на рисунке 2 нельзя разбить на прямоугольные треугольники, так как мы это проделали в предыдущем случае. Можно, например, попробовать дополнить наш многоугольник до «хорошего», нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей.
Однако оказывается, что есть очень простая формула, позволяющая вычислить площади таких многоугольников с вершинами в узлах квадратной сетки.
Эту формулу открыл австрийский математик Пик Георг Александров (1859 – 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика – Жюлиа, Пика – Невалины, доказал неравенство Шварца – Пика. Эта формула оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 г. польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники[2].
Она является классическим результатом комбинаторной геометрии и геометрии чисел.
Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям
сетки.
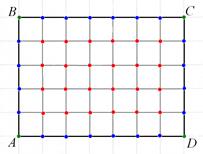 |
Обозначим через В - количество узлов, лежащих внутри прямоугольника, а через Г - количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки
вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов
– 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна
Г - 4
![]()
2
1 = В +
![]() 4
4
Г - 1 .
![]() 2
2
Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки,
мы установили формулу S = В +
Г - 1 . где S - площадь многоугольника, выраженная в площадях
![]() 2
2
единичных квадратиков сетки, Г – количество узлов сетки, лежащих на границах многоугольника, а В – количество узлов сетки, лежащих внутри многоугольника.
Это и есть формула Пика.
Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.
Эта формула является классическим результатом комбинаторной геометрии и геометрии чисел. В частности, площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на
сторонах (кроме вершин), равна
1 . Этот факт даёт геометрические доказательства формулы для
![]() 2
2
разницы подходящих дробей цепной дроби.
Я решила убедиться в том, что формула Пика верна для всех рассмотренных примеров. Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.
![]() Я рассмотрела
некоторые задачи на клетчатой бумаге с клетками размером 1
см 1
см и провел сравнительный анализ
по решению задач (Таблица№1).
Я рассмотрела
некоторые задачи на клетчатой бумаге с клетками размером 1
см 1
см и провел сравнительный анализ
по решению задач (Таблица№1).
 Таблица№1 Решение
задач различными способами.
Таблица№1 Решение
задач различными способами.
|
Рисунок |
По формуле геометрии |
По формуле Пика |
|
Задача №1 |
S=Sпр-(2S1+2S2) Sпр=4*5=20 см2 S1=(2*1)/2=1см2 S2=(2*4)/2=4см2 S=20-(2*1+2*4)=10 см2 Ответ:10 см². |
В = 8, Г = 6 S = 8 + 6/2 – 1 = 10 (см²)
Ответ: 10 см². |
|
Задача №2 |
a=2, h=4 S=a*h=2*4=8 см2
Ответ: 8 см². |
В = 6, Г = 6 S = 6 + 6/2 – 1 = 8 (см²)
Ответ: 8 см². |
|
Задача №3 |
S=Sкв-(S1+2S2) Sкв=42=16 см2 S1=(3*3)/2=4,5см2 S2=(1*4)/2=2см2 S=16-(4,5+2*2)=7.5 см2 |
В = 6, Г = 5 S = 6 + 5/2 – 1 = 7,5 (см²)
Ответ: 7,5 см². |
|
Задача №4 |
S=Sпр-(S1+S2+ S3) Sпр=4*3=12 см2 S1=(3*1)/2=1,5см2 S2=(1*2)/2=1см2 S3=(1+3)*1/2=2см2 S=12-(1,5+1+2)=7.5 см2 |
В = 5, Г = 7 S = 5 + 7/2 – 1 = 7,5 (см²)
Ответ: 7,5 см². |
|
Задача №5. |
S=Sпр-(S1+S2+ S3) Sпр=6*5=30 см2 S1=(2*5)/2=5см2 S2=(1*6)/2=3см2 S3=(4*4)/2=8см2 S=30-(5+3+8)=14см2
Ответ: 14 см² |
В = 12, Г = 6 S = 12 + 6/2 – 1 = 14 (см²)
Ответ: 14 см² |
|
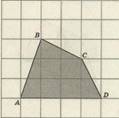
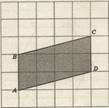
Задача №6.
|
Sтр=(4+9)/2*3=19,5 см2
Ответ: 19,5 см2 |
В = 12, Г = 17 S = 12 + 17/2 – 1 = 19,5 (см²)
Ответ: 19,5 см2 |


|
Задача №7. Найдите площадь лесного массива (в м²),
изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м |
S= S1+S2+ S3 S1=(800*200)/2=80000м2 S2=(200*600)/2=60000м2 S3=(800+600)/2*400= =280000м2 S=80000+60000+240000= =420000м2
Ответ: 420 000 м² |
В = 8, Г = 7. S 1 = 8 + 7/2 – 1 = 10,5 (см²) 1 см² - 200² м²; S = 40000 · 10,5 = 420 000 (м²)
Ответ: 420 000 м² |
|
Задача №8. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м. |
S=Sкв-2(Sтр+Sтрап) Sкв=800*800=640000 м2 Sтр=(200*600)/2=60000м2 Sтрап=(200+800)/2*200= =100000м2 S=640000-2(60000+10000)= 320000 м2
Ответ: 320 000 м² |
Решение. Найдём S 1 площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + Г - 1 2 В = 7, Г = 4. S 1 = 7 + 4/2 – 1 = 8 (см²) 1 см² - 200² м²; S = 40000 · 8 = 320 000 (м²) Ответ: 320 000 м² |
|
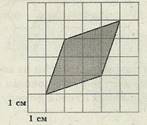
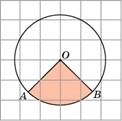
Задача №9. Найдите площадь Sсектора, считая стороны
квадратных клеток равными 1. В ответе укажите S . p |
Сектор является одной четвертой частью круга и, следовательно, его площадь равна одной четвертой площади круга. Площадь круга равна πR2, где R– радиус круга. В нашем случае R =√5 и, следовательно, площадь Sсектора равна 5π/4. Откуда S/π=1,25. Ответ. 1,25. |
Г= 5, В= 2, S = В + Г/2 – 1= 2 + 5/2 – 1= 3,5, S ≈ 1,11 p
Ответ. 1,11. |
![]()
![]()
|
Задача №10. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите S . p
|
Площадь кольца равна разности площадей внешнего и внутреннего кругов. Радиус R внешнего круга равен 2 2 , радиус rвнутреннего круга равен 2. Следовательно, площадь кольца равна 4 p и, следовательно, S = 4 . p Ответ:4. |
Г= 8, В= 8, S = В + Г/2 – 1= 8 + 8/2 – 1=11, S ≈ 3,5 p
Ответ:3,5 |
![]()
![]()
![]()
![]() Выводы: Из рассмотренных решений задач я увидела,
что некоторые из них, например
задачи
Выводы: Из рассмотренных решений задач я увидела,
что некоторые из них, например
задачи
№ 2,6, легче решить, применяя геометрические формулы, так как высоту и основание можно определить по рисунку. Но в большинстве задач требуется разбиение фигуры на более простые (задача №7) или достраивание до прямоугольника (задачи №1,4,5), квадрата (задачи №3,8).
Из решения задач №9 и №10 я увидела, что применение формулы Пика к фигурам, которые не являются многоугольниками, даёт приближённый результат.
Для того, чтобы проверить рациональность применения формулы Пика, я провела исследование на предмет затраченного времени (Приложение 1, таблица).
Вывод: из таблицы и диаграммы (Приложение 1, диаграмма 1) видно, что при решении задач с помощью формулы Пика, времени затрачивается гораздо меньше.
Нахождение площади поверхности пространственных форм
Проверим применимость этой формулы к пространственным формам. Найти площадь полной поверхности прямоугольного параллелепипеда, считая стороны квадратных клеток равными 1. К сожалению, подсчитать количество узлов решетки, попавших на границу параллелепипеда и внутрь параллелепипеда нельзя. Поэтому вычислить площадь полной поверхности по формуле Пика невозможно. Это недостаток формулы.
1. Решая задачи с практическим содержанием, (задачи №7,8; таблица №1), я решила применить данный способ для вычисления площади поверхности детали с одной стороны по формуле Пика и геометрическим способом (пришлось на чертеже деталь разделить на два прямоугольника и трапецию, сложить площади этих фигур и еще один прямоугольник, площадь которого вычиталась).
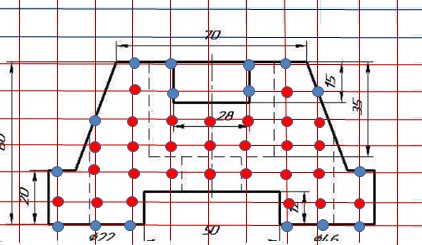
|
Расчет площади поверхности детали |
|
|
с помощью формулы Пика |
Геометрическим способом |
|
Г=16 В=27 S=В+Г-1=27+16-1=34 2 2 Масштаб 1клетка=9,8*9,8мм2 S=96,04*34=3265,36мм2 |
Разбиваем поверхность на две равные части, а одну часть на прямоугольники и трапецию S1= 22*12=264мм2 S2=8*47=376мм2 S3= 44+35•20=790мм2 2 S4= 15*14=210мм2 S=(S1+S2+S3+S4)•2=3280мм2 |
![]()
![]() Формула Пика вычисляет более просто, достаточно деталь нанести на клетки и подсчитать количество узлов, но она дала примерный результат от геометрического вычисления (погрешность по сравнению с геометрическим способом
вычисления 0,4%), т.е., если погрешность вычисления разрешается, то
формула Пика рациональна.
Формула Пика вычисляет более просто, достаточно деталь нанести на клетки и подсчитать количество узлов, но она дала примерный результат от геометрического вычисления (погрешность по сравнению с геометрическим способом
вычисления 0,4%), т.е., если погрешность вычисления разрешается, то
формула Пика рациональна.
Проанализировав результаты, я пришла к выводу: по формуле Пика в практическом применении вычисления площади можно найти гораздо проще, но результаты приблизительные.
Это связано с тем, что не все границы области являются сторонами многоугольников, и вершины не являются узловыми точками.
Проанализировав способы решения задач, можно сделать следующие выводы:
1) Формула Пика даёт быстрое и простое решение задач на нахождение площади фигуры, вершины которой лежат в узлах решётки, то есть нахождения площадей многоугольников.
2) Использование формулы Пика для нахождения площади кругового сектора или кольца нецелесообразно, так как она даёт приближённый результат.
В результате моей работы я расширила свои знания о решении задач на клетчатой бумаге, определил для себя классификацию исследуемых задач.
При выполнении работы были решены задачи на нахождение площади многоугольников, изображённых на клетчатой бумаге двумя способами: геометрическим и с помощью формулы Пика.
Решив задачи несколькими способами и получив одинаковые ответы, я пришла к выводу, что существуют случаи, когда удобнее применять формулу Пика, так как процесс разбиения фигур на части требует большего количества времени, а на экзамене оно ограничено. Кроме того, формула Пика позволяет решать более сложные задачи.
По моему мнению, формулу Пика может освоить любой ученик, достаточно уметь выполнять несложные математические вычисления.
Однако, наряду с достоинством формулы, есть и недостатки: формулу можно применить лишь для задач, фигуры в которых расположены на клетчатой решетке, вершины которых лежат в узлах решетки. Нахождение площади различных фигур, изображённых на клетчатой бумаге, позволило сделать вывод, что использование формулы Пика для вычисления площади кругового сектора и кольца нецелесообразно, так как она даёт приближённый результат, и, что формула Пика не применяется для решения задач в пространстве.
Анализ решений и эксперимент по определению затраченного времени показал, что применение формулы даёт возможность решать задачи на нахождение площади многоугольника, более рационально. Это позволяет экономить время на экзамене по математике.
Формула Пика —это настоящее спасение для тех учеников, которые так и не смогли выучить все формулы для вычисления площадей фигур, для тех, кто так и не уяснил до конца, как выполнить разбиение фигуры или дополнительное построение, чтобы подобраться к вычислению её площади «через знакомых». С другой стороны, для тех, кто площадь многоугольника, изображённого на клетчатой бумаге, умеет находить с помощью вышеперечисленных приёмов, формула Пика послужит дополнительным инструментом, с помощью которого можно будет решить задачу ещё и этим способом (и тем самым проверить правильность своего предыдущего решения, сверив полученные ответы).
Так же в работе были найдены площади различных территорий по формуле Пика, площади поверхности детали. Можно сделать вывод: использование формулы для нахождения площади различных территорий или деталей возможно, но результаты получаются приблизительными.
Выдвинутая мной гипотеза подтвердилась: формула Пика рациональна, проста, а значит полезна.
Я пришла к выводу, что тема, которая меня заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны. Поэтому я решила продолжить работу в этом направлении.
1. Васильев Н.Б. Вокруг формулы Пика, журнал «Квант» №12,1974 г., с.39-43.
2. Кушниренко А. Целые точки в многоугольниках и многогранниках, журнал «Квант» №4, 1977г., с.13-20.
3. Математический энциклопедический словарь. – Москва «Советская энциклопедия» 1988г.
4. Смирнов В. А. ЕГЭ. Математика. Задача В6. Планиметрия. Р/т. – М.: МЦНМО, 2011.
5. Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.
6. Задачи открытого банка заданий по математике ФИПИ, 2020 – 2021. Режим доступа: http://mathege.ru/or/ege/ShowProblems.html?posMask=32
7. Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика, журнал « Математика», 2009, № 17, с. 24-25.
Приложение 1
Сравнительный анализ времени, затраченного на решение задач
|
№ |
Геометрический способ |
По формуле Пика |
|
|
|
достраиванием |
по формуле |
|
|
1 |
5 минут |
|
2 мин |
|
2 |
2 минут |
24 секунд |
1 минут 15 секунд |
|
3 |
2 минут |
|
1 минут 20 секунд |
|
4 |
4 минут |
|
1 минут 30 секунд |
|
5 |
4 минут |
|
46 секунд |
|
6 |
|
25 секунд |
50 секунд |
|
7 |
|
4 минут |
3 минут |
|
8 |
|
4 минут |
3 минут |
|
9 |
|
5 минут |
2 минут |
|
10 |
|
5 минут |
2 минут |
|
Всего |
34 минут 36 секунд |
17 минут 41 секунд |
|
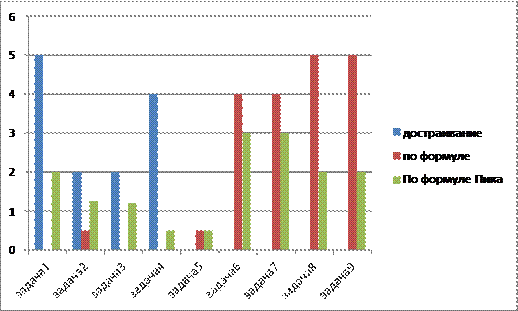 |
Приложение 2. Нахождение площади поверхности детали.
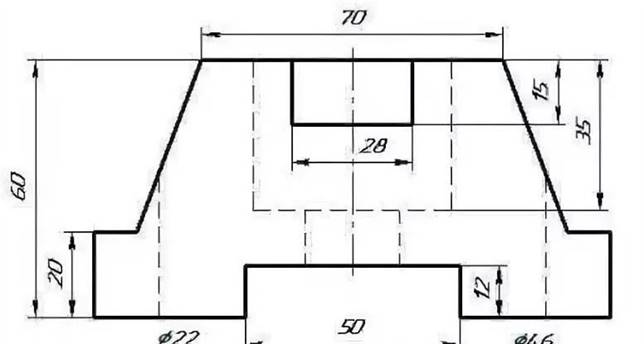 |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.