Проект по физике

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №7 г.Ртищево Саратовской области»

 

 

 

 

 

 

 

 

ИТОГОВЫЙ ПРОЕКТ ПО ФИЗИКЕ

 

 

«СТОЛКНОВЕНИЕ УПРУГИХ ШАРОВ»

 

 

 

 

Выполнил: Мочалов Александр,

обучающийся 9-А класса

Руководитель:    Громов И.Н.,

учитель физики

 

 

 

 

 

 

 

г.Ртищево, 2019г.

 

План.

1.    Введение. Цели и задачи проекта………………………………….стр.3

2.    Особенности абсолютно упругого удара………………………….стр.4

3.    Практическая часть ………………………………………………...стр.5

3.1.        Вывод формул скорости тел после их абсолютно упругого удара……………………………………………………………стр.5

3.2.        Различные вариации упругого соударения………………….стр.8

3.2.1. Столкновение шаров одинаковой массы………………...стр.8

3.2.2. Столкновение шаров, при неподвижном состоянии одного из них. ………………………………………………………….стр.9

3.2.3.Столкновение шара с плоской гладкой стеной. ………....стр.9

3.2.4. Нецентральный удар……………………………………стр.10

4.    Заключение…………………………………………………………стр.11

5.    Приложение ………………………………………………………..стр.12

6.    Литература …………………………………………………………стр.13

 

 

 

 

 

 

 

 

 

 

 

 

 

1.     Введение. Цели и задачи проекта.

В системе взаимодействующих тел, на которую не действуют внешние силы (такую систему называют замкнутой) имеется ряд величин, зависящих от  координат и скоростей  всех тел системы, которые при движении тел не изменяются с течением времени. К таким сохраняющимся величинам относятся импульс и энергия, которые подчиняются соответствующим законам сохранения. Они применимы как к телам обычных размеров, так и к космическим телам и элементарным частицам. Эти законы позволяют сравнительно простым путём, без рассмотрения действующих на тела сил решать ряд практически важных задач, в том числе определение скорости тел после их столкновения (или удара).

В природе встречаются два типа столкновений: абсолютно неупругий и абсолютно упругий удары.

На  уроках физики мы рассчитывали скорости тел при их неупругом взаимодействии, когда тела после удара соединяются и движутся как единое целое с общей скоростью. Например, столкновение пластилиновых шариков, попадание пули в ящик с песком, автосцепки вагонов, столкновение метеорита с Землёй и т. д. Тела в результате такого взаимодействия нагреваются, происходит потеря энергии за счёт перехода части механической энергии во внутреннюю. Такие задачи решаются довольно просто на основе закона сохранения импульса.

     В ходе моей работы над проектом «Столкновение упругих шаров», я получу ответ на основополагающий вопрос  «Как найти скорости тел при их упругом ударе?»

Мною выдвинута следующая гипотеза: « Для того, чтобы найти скорости тел после их упругого удара необходимо воспользоваться и законом сохранения импульса и законом сохранения энергии».

Цель моего проекта: получить расчётные формулы для нахождения скорости тел при их упругом столкновении.

Для реализации поставленной цели я буду решать следующие задачи:

ü  изучить теоретический материал по абсолютно упругому столкновению.

ü  вывести расчётные формулы для нахождения скорости тел при абсолютно упругом ударе;

ü  рассмотреть различные вариации абсолютно упругого удара.

 

2.    Особенности абсолютно упругого удара.

Изучив и проанализировав теоретический материал по теме «Абсолютно упругий удар», я  пришёл к следующим выводам.

1.     Абсолютно упругим ударом называется столкновение тел, в результате которого не происходит соединения тел в одно целое и тела после удара будут иметь скорости, отличающиеся как по модулю, так и по направлению. Например, столкновение бильярдных шаров, столкновение атомных ядер или элементарных частиц

2.     В системе упруго взаимодействующих тел потерь механической энергии  не происходит, поэтому внутренние энергии тел остаются неизменными (тела не нагреваются).

3.     В чистом виде такой удар среди обычных тел невозможен, так как процесс столкновения реальных тел всегда сопровождается возникновением сил трения, остаточных деформаций, излучением звуковых волн и другими процессами, ведущими к потере механической энергии  и  её  переходу в другие формы. Но, на практике эти потери энергии незначительны, поэтому в теории абсолютно упругого удара ими пренебрегают.

4.     Если потерями энергии можно пренебречь и систему упругих тел считать замкнутой, то  упругое столкновение тел можно описать не только законом сохранения импульса , но и законом сохранения энергии.

5.     Модуль и направления скорости взаимодействующих тел будут зависеть  от  модуля и направления импульса каждого тела и от его кинетической энергии.

 

 

 

 

 

 

 

 

3.    Практическая часть.

3.1.        Вывод формул скорости тел после их абсолютно упругого удара.

Поскольку тела после упругого  удара будут иметь разные скорости ,то применение одного закона сохранения импульса для описания данного взаимодействия будет недостаточно. Мы получим одно уравнение с двумя неизвестными. Значит, нужно ещё одно уравнение. Поскольку потерями энергии при абсолютно упругом ударе можно пренебречь, то второе уравнение  можно получить благодаря закону сохранения энергии. Что я и сделаю.

Рассмотрим упругий удар двух тел массами m₁ и m₂. Скорости тел до удара соответственно v_1х  и  v_2х . После удара соответственно  и  . Также, стоит отметить, что в данном случае, удар будет центральным, при котором скорости шаров до и после удара направлены по линии центров.

Сделаю рисунок с указанием направлением движения тел относительно координатной оси Х.

До упругого взаимодействия тел:

 

                   m₁v₁                                                         m₂v₂

                                                                                    Х

 

После упругого  взаимодействия тел:

 

               m₁                               m₂

                                                                                   Х

Закон сохранения импульса в проекции на координатную ось Х будет иметь следующий вид.

Закон сохранения механической энергии запишется так.

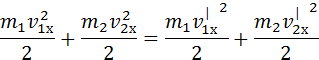
Для нахождения  ранее записанные выражения я объединю в систему и решу ее.

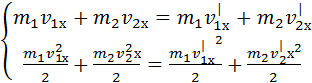     или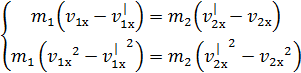     

 

 

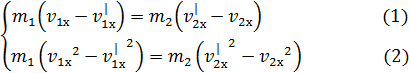
Почленно разделю уравнение (2) на уравнение (1).

 

Получаю:

                                            (3)

 

Умножу обе части уравнения (3) на.

 

                      (4)

В итоге получаю следующую систему уравнений:

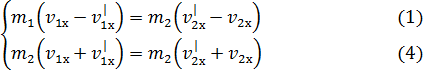
 Умножу обе части уравнения (1) на «-1».

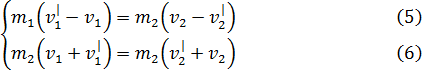
В каждом уравнении системы раскрою скобки и сложу полученные уравнения почленно. Таким образом, получаю:

После приведения подобных слагаемых в уравнении (7) , получим:

.

В итоге: 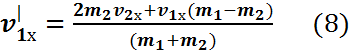  – скорость первого тела после соударения.

Для нахождения скорости я в уравнение (3) подставлю выражение (8).

Получаю:

 .

В итоге:

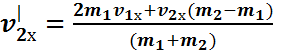(9) – скорость второго тела после упругого удара.

Таким образом, опираясь на законы сохранения импульса и энергии, мне удалось получить расчетные формулы для нахождения скорости тел после упругого удара этих тел.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.2. Различные вариации упругого соударения.

        Исследую полученные мною формулы  (8) и (9). Для этого рассмотрю различные вариации упругого соударения, а именно:

ü упругий удар шаров одинаковой массы;

ü упругий удар шаров, при неподвижном состоянии одного из них;

ü столкновение шара с гладкой стеной:

ü нецентральный удар.

 

3.2.1. Столкновение шаров одинаковой массы.

Предположим, что массы шаров одинаковы и соответственно равны:

.

В этом случае, формулы (8) и (9) для скоростей, соответственно, примут следующий вид:

  (10)

  (11)

На основании  полученных формул (10) и (11) можно сделать следующий вывод: «При  упругом столкновении шаров одинаковой массы, происходит взаимный обмен их скоростями».

С помощью данного утверждения можно объяснить отклонение шаров  в колыбели Ньютона.

Колыбель Ньютона — названная в честь Исаака Ньютона механическая система, предназначенная для демонстрации преобразования энергии различных видов друг в друга: кинетической в потенциальную и наоборот. Как правило, в Колыбели Ньютона задействованы 5 шаров, подвешенных на нитях. Если отклонить крайний шар, а потом отпустить его, то в движение придет лишь тот шар, который находится с другого края. Как и почему это происходит?

При упругом соударении шаров с одинаковыми массами, они обмениваются своими скоростями. Отклоненный шар будет обмениваться скоростью со вторым шаром, но так как все последующие шары неподвижны и прижаты друг к другу, то импульс  от отклонённого шарика будет передаваться сразу к последнему шарику и он будет приходить в движение, отклоняясь на угол, приблизительно равный углу отклонения первого шарика.

3.2.2. Столкновение шаров, при неподвижном состоянии одного из них.

Предположим, что шары имеют различные массы, а один из них находится в покое. Допустим
Тогда, формулы  (8) и (9) примут следующий вид:

 .

; .

Если же,

и .

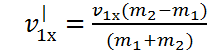При равных массах тел:;  

Таким образом, я пришёл к следующему выводу: «Если массы тел будут одинаковы, и одно из тел будет неподвижно, то неподвижное тело будет двигаться со скоростью налетающего тела, а налетающее тела будет покоиться».

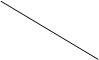
3.2.3. Столкновение шара  с плоской гладкой стеной.

При столкновении шара с гладкой плоской стеной нужно учитывать тот факт, что масса стены во много превышает массу шара. Помимо этого стена неподвижна.

                          m₁v₁

                                                              х

                                              

                        m₁v₂

Учитывая вышеизложенные факты, на основании закона сохранения импульса в проекции на ось х получу следующее равенство:
   или    . То есть при упругом ударе шара о стену, скорость шара не изменяется по модулю и будет равна скорости до столкновения, но изменится по направлению .

Так как SIN  A, то угол падения шара на стену будет равен углу отражения его от стены.

 

3.2.4. Нецентральный удар.

Рассмотрю случай нецентрального удара, упругого соударение тел, при котором меняются модули и направления скоростей, происходит «разлет» тел под углом друг к другу. Для упрощения рассмотрю удар тел одинаковой массы. Из закона сохранения импульса мы можем записать:

 

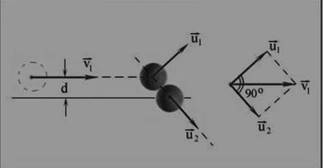
Из закона сохранения импульса, видно, что скорости шаров составят параллелограмм. А из того, что сохраняется кинетическая энергия, видно, что это будет не параллелограмм, а квадрат.  Значит:

Таким образом, при абсолютно упругом нецентральном ударе, когда массы шаров равны, они всегда разлетаются под прямым углом друг к другу.

4.    Заключение

Столкновения движущихся тел присущи всем уровням Мироздания – от микроскопического до космического, поэтому ударные явления весьма многообразны. Специфика ударов состоит в их интенсивности и скоротечности. Проблема удара важна не только для теоретиков, но и для конструкторов, автолюбителей, спортсменов. Ведь полученные знания упругого удара могут оказаться полезными, как при забивке свай, добыче руды так и при игре в мяч, в бильярд, гольф, кёрлинг. Следовательно, проблема удара важна не только для теоретиков, но и для конструкторов, автолюбителей, спортсменов и др.

Опираясь на законы сохранения импульса и энергии, мне удалось подтвердить выдвинутую мною гипотезу: «Для того, чтобы найти скорости тел после их упругого удара необходимо воспользоваться и законом сохранения импульса и законом сохранения энергии» и решить поставленные задачи.  С помощью основных законов сохранения в механике, я  получил расчетные формулы для нахождения скорости тел после их упругого удара. Полученные формулы я исследовал на предмет вариации различных упругих столкновений.  Кроме этого, я проверил истинность полученных мною формул практическим путём. Я нашёл скорости шаров различных масс  при упругом столкновении по формулам  (8), (9). А также решил  подобные задачи с помощью виртуальной модели «Столкновение упругих шаров» (СD «Открытая физика». Виртуальные лабораторные работы),( см. Приложение). Результаты, полученные расчётным способом  и с помощью модели, одинаковы. Таким образом, выведенные мною формулы, справедливы, а следовательно, я достиг цели своего проекта.

 

 

 

 

 

 

 

Приложение.

m1,кг	m2, кг	v1,м/с	v2, м/с	u1, м/с (расчёт)	u2 ,м/с (расчёт)	u1, м/с (модель)	u2 ,м/с (модель)
3	2	4	3	3,2	4,2	3,2	4,2
1	1	2	0	0	2	0	2
5	6	1	8	8,64	1,64	8,64	1,64

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.    Литература

1.     С.В. Громов, Н.В, Шаронова. Физика. 10 класс.-М.:Просвещение,2007

2.     СD «Открытая физика». Виртуальные лабораторные работы.

3.     https://studopedia.su/10_124968_absolyutno-uprugiy-i-neuprugiy-tsentralniy-udar.html

4.     https://ru.wikipedia.org/wiki/Колыбель_Ньютона

5.     http://uchitel.edu54.ru/node/193547

6.     https://studopedia.ru/10_133431_zakon-sohraneniya-impulsa.html

7.     https://interneturok.ru/lesson/physics/10-klass/bzakony-sohraneniya-v-mehanikeb/stolknovenie-tel-absolyutno-uprugiy-i-absolyutno-neuprugiy-udary

8.     https://studfiles.net/preview/5240163/

 

 

Скачано с www.znanio.ru