муниципальное бюджетное дошкольное образовательное учреждение        

         «Детский сад № 78»

 

 

 

 

 

 

Проект по интеллектуальном развитию

«В мире логики»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Составители:

Вахрамеева К.А.

 

 

 

 

2019 г.

г. Каменск-Уральский

«Не насильственно преподавать  милейший детям науку,

а посредствам науки, тогда ты лучше увидишь, кто к чему склонен»

                                                                                          Сократ

 

   Актуальность проекта заключается в изучении познавательных интересов и развитии логического мышления на занятиях и в повседневной жизни у детей дошкольного возраста,  в создании оптимальных условий для развития у них логического мышления через грамотное построение целостного педагогического процесса.

     Дошкольники проявляют высокую познавательную активность, они буквально забрасывают старших разнообразными вопросами об окружающем мире. Исследуя предметы, их свойства и качества, дети пользуются разнообразными обследовательскими действиями: умеют группировать объекты по цвету, форме, величине, назначению, количеству; умеют составить целое из 4-6 частей; осваивают счёт.

     Обучать детей нужно только в системе и на основе личностно – ориентированной модели общения,  которая направлена на развитие познавательных знаний, охрану его физического и психического здоровья, наличие между взрослыми и детьми отношений сотрудничества и партнерства.

     Только в этом случае ребенок, посещающий детский сад, в дальнейшем может  стать интересным, интеллектуальным человеком.

     Система Дьенеша, пожалуй, менее популярна среди родителей, чем, скажем, система Монтессори или Никитина. А между тем, логические игры этого замечательного венгерского педагога заслуживают самого пристального внимания. Ведь они способствуют развитию логического мышления, комбинаторики, аналитических способностей, формируют навыки, необходимые для решения логических задач: умение выявлять в объектах разнообразные свойства, называть их, адекватно обозначать словом их отсутствие, абстрагировать и удерживать в памяти одно, одновременно два или три свойства, обобщать объекты по одному, двум или трем, свойствам.

     Игры с блоками Дьенеша способствуют развитию речи: малыш вынужден строить высказывания с союзами "и", "или", частицей "не". Подобные игры способствуют ускорению процесса развития у дошкольников простейших логических структур мышления и математических представлений.

      Круг задач, решаемых методикой, достаточно обширен: это

• Развитие образного мышления (ощущения, восприятия, представление)
• Развитие логического мышления (анализ, синтез, сравнение, обобщение, классификация)

·         Развитие вариативности мышления творческих способностей, фантазии, воображения, конструктивных умений, увеличение объема внимания и памяти

• Развитие речи, умение высказывать и обосновывать свои суждения.

А самое главное, играть этими кубиками будет интересно и малышам двух-трех лет и пятилетним дошколятам. А некоторые игры заинтересуют даже первоклашек!

 

Цель:

Способствовать развитию логического мышления, интеллектуальных способностей через игры с блоками Дьенеша.

 

Задачи:

·           Познакомить детей с блоками Дьенеша.

·           Учить детей подбирать блоки по 1 свойству.

·           Отрицание свойства через его присутствие.

·           Введение карточек-схем.

·           Подбор блоков по 2-м, 3-м свойствам.

·           Подбор блоков по 4-м свойствам.

·           Расширять словарный запас.

·           Научить дошкольников решать логические задачи на различение по свойствам.

·           Научить выявлять в объектах разнообразные свойства, называть их.

·           Адекватно обозначать, словом их отсутствие.

·           Абстрагировать и удерживать в памяти 1,2,3 свойства.

·           Обобщать объекты по 1,2,3 свойствам с учетом наличия или отсутствия каждого.

·           Обеспечить целенаправленное решение задач по развитию мыслительных операций анализа, абстрагирования, обобщения, необходимых для освоения математических знаний.

·           Повысить интерес и активность детей на занятиях.

·           Обогатить формы работы на занятиях по математике, вне занятий, в свободное от занятий время.

 

Краткая аннотация проекта.

Организация опытно – экспериментальной деятельности проходит в форме партнерства взрослого и ребенка, что способствует развитию у воспитанников активности, самостоятельности, умению принять решение, пробовать делать что – то, не боясь, что получится неправильно, вызывает стремление к достижению, способствует эмоциональному комфорту, развитию социальной и познавательной деятельности.

 

Участники проекта: дети разновозрастной группы, воспитатели, родители.

 

Срок реализации: 1 сентября – 30 мая.

 

Основные этапы реализации проекта:

1 этап: (подготовительный) — сентябрь 2019 г.

Цель: создание условий, необходимых для реализации проекта.

2 этап: (основной) — октябрь 2019 г. – май 2020 г.

Цель: реализация основных видов деятельности по направлениям проекта.

3 этап: (заключительный) — май 2020 г.

Цель: анализ полученных результатов. Презентация проекта.

 

Тип проекта: познавательно – игровой

 

Содержание проекта:

Формы работы	Ответственные	Сроки исполнения
I этап (подготовительный)
1.Изучение и подбор методической литературы по направлению проекта.	Воспитатели	сентябрь
2. Подбор дидактических игр, наглядного материала, художественной литературы, картотеки логических игр, изготовление дидактического материала и игр своими руками.	Воспитатели	сентябрь
3. Разработка перспективного планирования	Воспитатели	сентябрь
II этап (основной)
1.      Работа с детьми
а. Совместная   и   непрерывная   образовательная деятельность	Воспитатели	октябрь - май
б. Дидактические, пальчиковые и подвижные  игры  по  проекту.	Воспитатели
в. Наблюдения, беседы, рассматривание картинок.	Воспитатели
г. Продуктивная деятельность.	Воспитатели
2.      Работа с родителями
а. Наглядная пропаганда.	Воспитатели	октябрь - май
б. Консультации, рекомендации, буклеты.	Воспитатели
в. Конкурсы:	Воспитатели
г. Вечер встреч.	Воспитатели
3.      Оформление  развивающей  предметно - пространственной среды		октябрь - май
III этап (заключительный)
1. Презентация проекта «В мире логике»	Воспитатели	сентябрь 2020 г.
2.   Оформление фотоотчета по проекту.	Воспитатели	сентябрь 2020 г.

 

 

 

Перспективное планирование по проекту «В мире логике»  на 2019-2020 учебный год.

 

Дата/месяц	Тема	Задача	Методические приемы
Сентябрь	Знакомство с блоками Дьенеша.	Ускорение процесса развития у дошкольников простейших логических структур мышления и математических представлений. Решение логических задач на разбиение по свойствам.	- Знакомство со свойствами блоков Дьенеша. - Назвать все фигуры по заданным свойствам. - Построить цепочку с разными вариантами свойств. - Участвуют 4 ребёнка; фигуры делятся поровну; каждый ребёнок по очереди делает свой ход, при отсутствии фигуры ход пропускается. Выигрывает тот, кто первым выложит все фигуры.
Октябрь	Знаки - символы	Использование знаков – символов способствует развитию у детей способности к моделированию свойств, их замещению, освоению операции кодирования и декодирования информации о свойствах блоков. Учить анализировать материал по строчкам или столбцам таблицы и выявлять ошибки.	Определять блоки по: 4 символам формы (круг, квадрат, треугольник и прямоугольник); по: 2 символам размера (большой, маленький); по: 3 символам цвета (красный, синий, жёлтый); по: 2 символам толщины (толстый, тонкий); по: 11 знакам - символам с отрицанием этих свойств (если не красный – то синий или жёлтый и т.д.)
Ноябрь	Примеры упражнений на освоение знаков - символов.	Научить детей самостоятельно выявлять свойства блоков, как по слову, так и с использованием карточек.	Освоение способа декодирования с помощью карточек со знаками - символами. - Развивать умение группировать блоки по двум - трём свойствам. - Разделить фигуры так, чтобы у «мишки» оказались все синие, а у «зайки» все квадратные.  - Выстроить фигуры в один ряд, чтобы во втором ряду были по каждой фигурой другие, описать каждую.
Декабрь	Освоение детьми средств и способов познания.	Освоение детьми идеи видоизменения. Научить составлять описание свойства блока, пользуясь моделью.	Детям надо пройти сквозь «волшебную» дверь и свойства их блоков изменяться. Описать, что изменилось? – изменяя каждый раз игровую мотивацию, получать разные по свойствам фигуры. - Научить детей группировать объекты по определённым признакам, находить ошибки при группировке.
Январь	«Читаем» схемы, следуем правилам.	Побуждать детей к самостоятельному составлению новых правил, игровых задач, проявлению активности и творчества. Учить работать по схемам с правилами.	- Построить дорожки  для пешеходов и автомобилей в городе Фигур. Для этого дети изучают схемы, вводят правила игры, которые требуют ориентировки на два свойства блоков. - Выращивать деревья с помощью логических блоков и палочек. - Стимулировать творческие проявления, сначала дети работают по готовым правилам, потом составляют их сами. - С помощью правил и схем сократить слово.
Февраль	Анализируем, сравниваем, находим закономерности.	Учить детей использовать таблицы, которые требуют анализа, сравнения и обобщения рядов фигур по трём свойствам. Развивать умение сравнивать предметы по одному – четырём свойствам; понимание слов: «Разные»,  «Одинаковые»; подведение к пониманию отрицания свойств. Развивать умение анализировать  форму предметов; сравнивать по их  свойствам; развивать художественные  способности (выбор цвета, фона,  расположения композиции).  Развивать умения выявлять и абстрагировать свойства; развивать умения рассуждать, аргументировать свой выбор.	- Учить детей решать логический  квадрат, находить недостающую фигуру и класть её в клетку, где нарисованы Винни - Пух и Пятачок. - В игре в одну лапу медведю даю любой блок, во вторую подбирают по  правилам. - «Написать картины» по эскизам; бумагу, фон, детали, блоки дети выбирают сами; на контур ставят тонкий блок, на окрашенную деталь - толстый. Устраивают выставки.  Дети покупают три игрушки на «денежки» - 3 логические фигуры,   у которых есть хотя бы одно свойство, два свойства.
Март	Разработка авторских игр	Учить  детей сравнивать предметы по одному – четырём свойствам; пониманию слов: Подбор и разбиение платьев по (2, 3, 4 свойствам). «Самоцветы». Подобрать по 1 – 4 свойствам). Расшифровать свойства самоцветов с помощью знаков  - символов и решения примеров.	Обыграть игровые ситуации: В первом варианте находить платья  разные, одинаковые; подвести к пониманию отрицания свойств; учить расшифровывать с помощью знаков - символов, решать примеры каждого задания.
Апрель	Ориентируемся на знаки – символы отрицания свойств и расшифровываем	Продолжать учить детей работать со схемами, со знаками - символами, отрицанием свойств, декодированием.	-Для поддержания интереса к игре воспитатель наделяет фигуры и блоки различными образами; дети находят блоки по схемам, знакам - символам; помогают блокам выбраться из чащи. - Учить детей подбирать карточки   по образцу (по свойствам) - Учить детей анализировать, читать схему, кодировать и декодировать информацию. - Воспитатель показывает карточки – загадки изображающие свойства блоков, дети отгадывают, достают нужный блок. Выигрывает тот у кого больше блоков.
Май	Развитие памяти, внимания, навыков самоконтроля.	Учить анализировать, читать схему; уметь кодировать и декодировать информацию, учить ориентироваться на плоскости. Учить работать в коллективе.	- Игра проводится между двумя командами: кто быстрее выложит дорожку из плиток. - Ребенок, пряча блок, кодирует его в таблице. Воспитатель - отгадывает по признакам и символам. - Ребёнок выбирает блок и описывает его с помощью знаков - символов, затем записывает в бланк - заказ. - Дети выбирают жетоны, надевают их и встают в круг. Читают считалку, на последних словах кот надевает свой жетон, на нём информация для мышей - кого он будет ловить.

 

 

Список литературы

1.      Н. Захарова: Играем с логическими блоками Дьенеша. Учебный курс для детей 5-6 лет. ФГОС , Детство-Пресс, 2017 г.,272с.

3. Бондаренко А. К. Дидактические игры в детском саду: Кн. для воспитателя дет. сада. – 2-е изд., дораб. – М.: Просвещение, 1991. – 160 с.: ил.
4. Векнер Л. М. Психические процессы - т. 2, Мышление и интеллект- Л.: изд. Ленингр. Ун-т им. А. А. Жданова,1976.- 342с.
5. Возрастные возможности усвоения знаний. / Под ред. Д. Б. Эльконина и В. В. Давыдова- М.: Изд. «Просвещение»,1966.- 442с.
6. Воспитателю о детской игре.: Пособие для воспитателей детского сада/ Под ред. Т. А. Марковой. – М.: Просвещение, 1982. – 128 с., ил.
7. Выготский Л. С. Избранные психологические исследования. Мышление и речь. Проблемы психологического развития ребенка- М.: Изд. Акад. пед. Наук РСФСР,1956.- 520с.
8. Гринченко И. С. Игра в теории, обучении, воспитании и коррекционной работе. Учебно-методическое пособие – М.: «ЦГЛ», 2002. – 80 с.
9. Детство: Программа развития и воспитания в детском саду/ В.И.Логинова, Т.И. Бабаева, Н.А.Ноткина и др.; под ред. Т.И.Бабаевой, З.А.Михайловой, Л.М.Гурович: Изд. – 3-е, переработанное. – СПб.: Акцидент, 2002. – 224с.
10. Дурова Н. В., Новикова В. П. Ступеньки к познанию./ Худ. Ю. В. Богатова. – СПб.: ДЕТСТВО_ПРЕСС, 2003. – 56 с.: ил.
11. Запорожец А. В. Значение ранних периодов детства для формирования детской личности. Принцип развития в психологии. М. 1978, с.243- 267
12. Игры и упражнения по развитию умственных способностей у детей дошкольного возраста: Кн. для воспитателя дет. cада/ Л. А. Венгер, О. М. Дьяченко, Р. И. Говорова, Л. И. Цеханская; Сост. Л. А. Венгер, О. М. Дьяченко. – М.: Просвещение, 1989. – 127 с.: ил.
13. Касабуцкий Н.И., Скобелев Г.Н., Столяр А.А. Давайте поиграем: Математические игры для детей 5-6 лет: Кн.для воспитателей детского сада и родителей/ под редакцией А.А.Столяра. – 2-е изд. – М.: Просвещение; учебная литература, 1996. – 112с.
14. Катаева А. А., Стребелева Е. А. Дидактические игры и упражнения в обучении дошкольников с отклонниями в развитии: Пособие для учителя. – М.: Гуманит. изд. центр ВЛАДОС, 2001. – 224 с.: ил.
15. Коломенских Я. Л., Панько Е. А. Детская психология., Мн. «Университетское», 1988, - 223с.
16. Леонтьев А. Н. Проблемы развития психики, 4-е изд., М.: Изд. Москов. ун-та,1981.- 584с.
17. Логика и математика для дошкольников: Методическое пособие/ Авт.-сост. Е.А.Носова, Р.Л.Непомнящая/ (библиотека программы «Детство»). – СПб.: Акцидент, 1997. – 79с.
18. Математика до школы: Пособие для воспитателей детских садов и родителей. – Ч.1: Смоленцева А.А., Пустовой О.В. Математика до школы. Ч.2.: Игры-головоломки/ сост. З.А.Михайлова, Э.Н. Иоффе; Худ.И.Н.Ржевцев, - СПб.: Акцидент, 1997. – 176с.
19. Мхайлова З.А. Игровые занимательные задачи для дошкольников: Кн. Для воспитателей детских садов. – 2-е изд., дораб. – М.: Просвещение, 1990. – 94с.
20. Морозова Н.Г. Формирование познавательных интересов у детей дошкольного возраста с отклонениями в развитии // Особенности развития и воспитания детей дошкольного возраста с недостатками слуха и интеллекта / Под ред. Л. П. Носковой - М.,1984.- с.65- 73
21. Перова М. Н. Дидактические игры и упражнения по математике для работы с детьми дошкольного и младшего школьного возраста: Пособие для учителя. – 2-е изд., перераб. – М.: Просвещение, Учебная литература, 1996. – 144 с.: ил.
22. Пиаже Жан Избранные психологические труды. Психология интеллекта. Генезис числа и ребенка. Логика и психология. (Пер. с фр. Предисл. В. А. Лекторского и др., с.9- 53)- М.: «Просвещение»,1969.- 659с.
23. Психологический словарь. / Под ред. В. В. Давыдова, А. В. Запорожца, Б. Ф. Ломова и др.; Науч.-исслед. ин-т общей и педагогической психологии. Акад. пед. наук СССР. – М.: Педагогика, 1983 – с. 200-201.
24. Рубинштейн С. Л. Проблемы общей психологии / отв. Ред. Шорохова Е. В.- М.: «Педагогика»,1973.- 423с.
25. Сорокина А. И. Дидактические игры в детском саду: (Ст. группы). Пособие для воспитателей дет. сада. – М.: Просвещение, 1982. – 96 с.
26. Стребелева Е. А. Формирования мышления у детей с отклонениями в развитии: Кн. для педагога-дефектолога. – М.: Гуманит. изд. центр ВЛАДОС, 2001. – 184 с.: ил. – (Коррекционная педагогика).
27. Юнг К. Г. Аналитическая психология: прошлое и настоящее / К. Г. Юнг, Э. Сэмюэлс, В. Одайник, Дж. Хаббек; сост. В. В. Зеленский, А. М. Рудкевич - М: Мартис,1995.- 320с.

 

Этапы работы

Исходя из всего вышеизложенного, были намечены следующие этапы работы:

1.     Провести анализ предыдущей деятельности, форм и методов работы с детьми старшего дошкольного возраста.

2.     Ознакомиться с опытом педагогов – коллег, работающих по данной схеме.

3.     Изучить научную литературу, характеризующую психические особенности развития детей пятого года жизни.

4.     Подготовить развивающую среду с учетом возрастных особенностей детей.

5.     Конкретно обозначить виды игр, посредством которых будет проводится целенаправленная работа педагога (игры, активизирующие мышление ребенка, способствующие усвоению им отдельных логических операций).

6.     Составить план – схему использования игр в совместной и самостоятельной деятельности.

7.     В течение всего временного промежутка (учебный 2010 – 2012 год) наблюдать за особенностями формирования навыков логического мышления (наглядно – образного) у каждого конкретного ребенка.

В виду того, что математические способности это совокупность специфических компонентов, в работе с детьми были поставлены следующие задачи:

1. Знакомить детей с геометрическим фигурами и формой предметов,
размерами, цветом. Научить выявлять и абстрагировать в предметах одно свойство (цвет, форму, размер, толщину).

2. Развивать мыслительные умения: сравнивать, анализировать,
классифицировать, обобщать предметы: по одному из этих свойств; по двум свойствам (цвету и форме, форме и размеру, размеру и толщине); по трем свойствам (цвету, форме и размеру; размеру, форме и толщине).

3.     Учить детей овладению приемами замещения и моделирования свойств,
умению кодировать и декодировать информацию о них, используя
слова: «и», «или», «не», «все», «любой», «каждый».

4.     Учить усваивать элементарные навыки алгоритмической культуры
мышления: счету и счетным операциям при помощи чисел, измерения, вычисления.

5.     Учить оперировать знаниями о цвете, величине, форме, развивать умение ориентироваться в пространстве.

6.     Развивать познавательные процессы: восприятие, память, внимание, воображение; умение составлять различные воображаемые предметы, фантастические образы из блоков Дьенеша.

В дошкольной дидактике имеется огромное количество разнообразных дидактических материалов. Однако возможность формировать в комплексе все важные для умственного развития, в частности математического развития, мыслительные умения дают немногие. Основные особенности блоков Дьенеша - абстрактность, универсальность, высокая эффективность. Этот дидактический материал помогает осваивать сенсорные эталоны цвета, формы, величины, тренирует тактильно-осязательные анализаторы. Способствует максимальному развитию мелкой моторике рук, речи, что немаловажно для совершенствования математических способностей.

Дидактический материал «Логические блоки» состоит из 48 объемных геометрических фигур, различающихся по форме, цвету, размеру и толщине. В процессе разнообразных действий с логическими блоками (разбиение, выкладывание по определенным правилам, перестроение и др.) дети овладевают различными мыслительными умениями, важными как в плане предматематической подготовки, так и с точки зрения общего интеллектуального развития. К их числу относятся умения анализа, абстрагирования, сравнения, классификации, обобщения, кодирования – декодирования, а также логические операции «не», «и», «или». В специально разработанных играх и упражнениях с блоками у малышей развиваются элементарные навыки алгоритмической культуры мышления, способность производить действия в уме. С помощью логических блоков дети тренируют внимание, память, восприятие.

Для решения поставленных задач была продумана система работы, которая включает в себя:

• создание определенной предметно-развивающей среды в группе;
• разработка перспективно-тематического плана занятий по математике на старшую и подготовительную группу;
• разработку конспектов тематических занятий по математике для старшей и подготовительной группы на год с использованием блоков Дьенеша;
• систематизация игр с блоками Дьенеша;
• составление сценариев праздников и развлечений с математическим содержанием;
• изготовление нестандартных дидактических игр математического содержания использование данного дидактического материала.

Таким образом, в группе был оформлен центр развивающих игр, где в постоянном доступе (наряду с другими играми) располагались блоки Дьенеша, периодически лишь варьировались и усложнялись игровые задания.

На первом этапе, прежде чем приступить к целенаправленным играм и упражнениям, детям была предоставлена возможность самостоятельно познакомиться с логическими блоками и палочками. Дети использовали их по своему усмотрению в разных видах деятельности. Наблюдая за детьми, педагог делала выводы о степени мыслительной деятельности каждого ребенка, находила ту «ступень», с которой следует начинать движение вперед. Для начального этапа подбирались самые простые игры, цель которых в усвоении свойств, слов «такой же», «не такой» по форме, размеру, толщине.

1) - «Найди все фигуры (блоки) как эта по цвету (размеру, форме)»;

- «Найди не такую фигуру как эта по цвету (размеру, форме)»;

2) - «Найди все такие фигуры как эта по цвету и форме (по форме и
размеру, размеру и цвету)»;

«Найдите не такие фигуры, как эта по цвету и размеру (по форме и
размеру и т.п.)»;

«Найдите такие же, как эта по цвету, но другой формы или такие же по форме, но другого размера и т.п.».

3) Предлагались детям игры и более сложного варианта: найдите такие
же, как предъявляемая фигура по цвету и форме, но другие по размеру и т.п.
А в игре «Цепочка» было предложено от произвольно выбранной фигуры
построить как можно более длинную цепочку:

- чтобы рядом не было фигур одинаковых по форме (цвету, размеру);

- чтобы рядом не было фигур одинаковых по форме и размеру (цвету и
размеру и т.п.);

- чтобы рядом были фигуры одинакового цвета (формы, размера).

В игре «Второй ряд» детям предлагалось выложить в ряд 5 — 6 любых
фигур. Построить под ними второй ряд, но такой, чтобы под каждой фигурой
верхнего ряда оказалась фигура другой формы (размера, цвета); такой же
формы (цвета, размера) и т.п.

В игре «Домино» одновременно могут участвовать не более четырех детей. Фигуры делятся поровну между участниками. При отсутствии фигуры

ход пропускается. Выигрывает тот, кто первым выложит все фигуры. Ходить

можно по разному:

Фигурками другого цвета (размера);

Фигурками того же цвета (размера), но другой формы и т.п.

6) В игре «Раздели фигуры» используются игрушки. Предлагается

разделить все фигурки между игрушками. Необходимо, чтобы дети

разделили правильно, предлагать ответить на вопросы:

Какие фигурки оказались у мишки? (все красные)

А у зайки? (все не красные).

Можно предложить разделить по-другому: чтобы у мишки оказались все

крупные, чтобы у зайки оказались все толстые.

После этого усложняются игровые правила:

Разделите все фигуры так, чтобы у мишки оказались все сини, а у зайки все
квадратные.

У мишки оказались все треугольные, а у зайки все большие.

У мишки оказались все некруглые, а у зайки все желтые.

Видя, что дети хорошо справляются с данными заданиями можно еще усложнить: «Раздели фигуры»

Какие фигуры достались Буратино? (круглые, не желтые, маленькие).

Какие фигуры получил Чебурашка? (желтые, маленькие, не круглые).

- Какие достались сразу и Буратино и Чебурашке? (круглые, желтые,
маленькие) и т.п.

- Какие оказались ничьи? (большие, не круглые, не желтые).

В работе с детьми используются опорные карточки-символы, которые помогают быстро сориентироваться при выполнении задания, правильно построить свой ответ и подробно описать результат действий. Так цвет обозначается пятном, а цвет пятна обозначается буквой («К», «Ж», «С»), форму – соответственно контурами фигур, толщину условными обозначениями человеческой фигуры (толстый и тонкий), величину - силуэтом дома (высокий и низкий).

Пользуясь карточками, дети называют имя каждого блока. В словаре детей появились такие определения: «Это красный, большой, круглый, толстый». На карточке обозначен красный цвет, значит сюда можно положить красный блок. Задание постепенно усложнялись. И дети постепенно выявили свойства блоков, как по слову, так и с использованием карточек. Педагог предлагает детям игры: «Кто быстрее соберет блоки?», «Поручение», «На свое место» и следила, чтобы дети выполняли все быстро и качественно, чтобы блоки в данных играх были в поле зрения играющих -это обеспечивало детям опору на непосредственном восприятии свойств блока при решении задач.

Промежуточная диагностика (2011 г.) показала положительную динамику развития математических способностей, логического мышления детей и качества усвоения программного материала. Количество детей с высоким уровнем развития повысилось на 5%, со средним уровнем - на 9,5%, с низким уменьшилось на 10%.

Наблюдая за использованием игр детьми, видя повышенный интерес к ним, я разработала цикл занятий с включением данного дидактического материала на основе программы «Детство». Был составлен перспективный план на старшую и подготовительную группу, где предусматривалось постепенное усложнение, как всего материала, так и игровых заданий с блоками Дьенеша. (Приложение №1).

Все занятия планировались в игровой форме: это и путешествие, и полет на космическом корабле и путешествие в город геометрических фигур. Детям предлагается помочь попавшему в беду герою, разобраться в сказочной ситуации — все это стимулирует интерес к занятию, умственную деятельность. Практика показала, увлеченные игрой дети быстро усваивают материал, приобретают нужные умения, навыки мыслительной деятельности, такой подход предупреждает утомляемость.

Планируя педагогическую деятельность на неделю, необходимо проследить взаимосвязь учебных занятий и других видов детской деятельности. Таким образом, знания, полученные ребенком на занятии, закрепляются в совместной деятельности, после чего переходят в самостоятельную и уже после этого – в бытовую.

Результаты первичного обследования позволяют распределить детей на три группы: с высоким, средним и низким уровнем развития.Error: Reference source not found Такое разделение помогает ориентироваться в подборе занимательного материала и задач, предупреждает возможные перегрузки «слабых» детей, потерю интереса (ввиду отсутствия усложнений) – у «сильных». Детям, справляющимся с логическими задачами на среднем уровне, предлагаются варианты подобных задач, а так же игры соревновательного характера.

Особый подход необходим к «слабым» детям. Учитывая их психические и физические особенности, необходимо внушить им уверенность в себе, подвести к самостоятельному решению простых задач. В случае быстрого утомления, предусмотреть смену вида деятельности. Детям с высоким уровнем развития: отлично справляющимися с конкретной задачей предлагается «подключаются» к тем, кто испытывает серьезные трудности. Такая форма взаимодействия педагога и воспитанников очень эффективна. Она помогает сплотить коллектив, дает возможность самоутвердиться успевающим детям и почувствовать уверенность в своих силах – более слабым.

Задача последующих занятий усложнялась: у детей развивалось умение выявлять свойства блоков по слову, без опоры на наглядность. Блоки убирались под салфетку, а игровые образы помогали заинтересовать детей в отборе - «запасов на зиму» в «норку» (коробку), выбирая по слову ведущего либо красные, либо круглые. Успешно проводились и другие игры: «Засели домики», «Кто быстрее спрячет». Победителями оказывались те дети, кто первым и безошибочно выполнит задания.

Далее дети знакомились со словами и знаками, обозначающими отсутствие свойств. Например:

Предлагала детям игры: «Переводчик», «Помоги Незнайке». В этих играх дети рассказывали Незнайке о блоках, переводили в слова то, что обозначает карточка, научили Незнайку по-разному рассказывать про цвета, величину. А в играх «На свою веточку», «Кто хозяин?», «Найди выход» - дети учились оперировать одновременно двумя свойствами.

Не вызывали у детей трудностей и логические игры с кругами. У них формируется четкое представление о внутренней и внешней области по отношению к некоторой замкнутой линии. Например: имеется один круг. У каждого ребенка в руках один блок. Дети по очереди располагают блоки в соответствии с заданием педагога (внутри круга все красные блоки, а вне круга — все остальные). После чего детям задавались такие вопросы: какие блоки лежат внутри круга? (красные); какие оказались вне круга? (не красные). Верен именно такой ответ, так как важно лишь то, что внутри круга лежат все красные блоки, и никаких других там нет, а свойство блоков вне круга определяется через свойство тех, которые лежат внутри.

Я проводила игры с двумя кругами, давала два разноцветных круга (синий и красный), круги пересекаются, поэтому имеют общую часть. Детям давалось задание: расположить круги так, чтобы внутри синего круга оказались все круглые блоки, а внутри красного круга все красные. На первых порах дети затруднялись, куда положить красные и круглые блоки (их место в общей части двух кругов). После выполнения задания дети отвечали на вопросы:

Какие блоки лежат внутри обоих кругов?

Внутри синего, но не красного?

Внутри красного, но вне синего?

Вне обоих кругов?

С помощью одной игры можно решать большое количество образовательных задач. Незаметно для себя дети осваивают и запоминают цвет, форму, величину и толщину предмета, тренируют мелкую моторику рук, совершенствуют речь, мышление, внимание, память и воображение.

С одной и той же игрой могут заниматься дети трех - семи лет. Это возможно потому, что к простому физическому манипулированию присоединяется система постоянно усложняющихся развивающих вопросов и познавательных заданий. Игру существенно дополняет сказка. Она вводит ребенка в «необыкновенный мир» возможностей и замыслов, заставляет содействовать и сопереживать героям и событиям.

Результативность опыта

Диагностическое обследование выявления уровня развития логического мышления проводилось на основании выделенных в программе «Детство» уровней развития:

Низкий: ребенок выделяет свойства предметов (двух-трех), определяет наличие/отсутствие признака. Считает, сравнивает, измеряет. Затрудняется в речевом выражении своих действий, связей, групп, количественных и пространственных отношений. В играх пользуется образцами, инициативы и творчества не проявляет.

Средний: ребенок выделяет свойства предметов, фигур, самостоятельно классифицирует их. Затрудняется в выделении предполагаемых изменений при смене основания классификации, числа предметов в образованных группах, условной мерки. Самостоятельно составляет алгоритм, выполняет заданные им действия, поясняет последовательность. Результаты действий носят в основном воспроизводящий характер.

Высокий: ребенок имеет обобщенные представления о свойствах предметов, выделяет самостоятельно основание классификации, замечает и выражает в речи изменения, связи и зависимости групп предметов, чисел, величин. Владеет способом воссоздания геометрических фигур, силуэтов, проявляет интерес и творчество в интеллектуальных играх. Не испытывает затруднений в играх, выполнении учебных программ, пользуется условными обозначениями.

Критерии	Обследование на начальном этапе	Обследование на заключительном этапе	Примечание (положительность результата)
1) Способность к формализации математического материала, к отделению формы от содержания, абстрагированию от конкретных количественных отношений и пространственных форм и оперированию формальными структурами, структурами отношений и связей;	В - 0 С – 3 – 25% Н – 9 – 75%	В – 5 – 42% С – 6 – 50% Н – 1 – 8%	В – на 42% С – на 25% Н – на 67%
2) Способность обобщать математический материал, вычленять главное, отвлекаясь от несущественного, видеть общее во внешнем различном;	В – 1 – 8% С – 3 – 25% Н – 8 – 66%	В – 6 – 50% С – 5 – 42% Н – 1 – 8%	В – на 42% С – на 17% Н – на 58%
3) Способность к оперированию числовой и знаковой символикой;	В – 2 – 16% С – 5 – 42% Н – 5 – 42%	В – 7 – 58% С – 5 – 42% Н - 0	В – на 42% С – на 0 % Н – на 42%
4) Способность к «последовательному, правильно расчленённому логическому рассуждению», связанному с потребностью в доказательствах, обосновании, выводах;	В - 0 С – 2 – 16% Н – 10 – 83%	В – 4 – 33% С – 5 - 42% Н – 3 – 25%	В – на 33% С – на 26% Н – на 58%
5) Способность сокращать процесс рассуждения, мыслить свернутыми структурами;	В - 0 С – 2 – 16% Н – 10 – 83%	В – 4 – 33% С – 5 - 42% Н – 3 – 25%	В – на 33% С – на 26% Н – на 58%
6) Способность к обратимости мыслительного процесса (к переходу с прямого на обратный ход мысли);	В - 0 С – 4 – 33% Н – 8 – 66%	В – 4 – 42% С - 5 - 42% Н – 3 – 25%	В – на 42% С – на 9% Н – на 41%
7) Гибкость мышления, способность к переключению от одной умственной операции к другой, свобода от сковывающего влияния шаблонов и трафаретов;	В - 0 С –4 – 33% Н – 8 – 66%	В – 4 – 33% С - 6 – 50% Н – 2 – 16%	В – на 33% С – на 17% Н – на 50%
8) Математическая память, память на обобщения, формализованные структуры, логические схемы;	В – 1 – 8% С – 5 – 42% Н – 6 – 50%	В – 4 – 33% С - 6 – 50% Н – 2 – 16%	В – на 25% С – на 8% Н – на 34%
9) Способность к пространственным представлениям.	В - 0 С – 4 – 33% Н – 8 – 66%	В – 4 – 33% С – 7 – 58% Н – 1 – 8%	В – на 33% С – на 25% Н – на 58%

В работе использовались игровые методики обследования, которые позволили максимально эффективно выявить уровень развития математических способностей каждого ребенка. Методики предъявлялись детям в первой половине, индивидуально, последовательно. Обработка результатов производилась путем оценки уровня развития способностей детей по 4-х бальной системе:

• 4 балла - справился с задачей без дополнительных вопросов, дав правильный четкий ответ, полное связное описание действий;
• 3 балла - справился с задачей, дав правильный, но недостаточно четкий полный ответ, сделал одну поправку, педагог не задавал дополнительных вопросов, не полное объяснение своих действий;
• 2 балла - справился с задачей с помощью наводящих вопросов, сделал две поправки и одну ошибку (педагогом предъявлялась вспомогательная картинка), непоследовательное объяснение своих действий;
• 1 балл - справился с задачей после применения приема припоминания, сделал не более трех ошибок (педагогом предъявлялась вспомогательная картинка). Нет связного описания действий, ответы на поставленные вопросы фрагментарны, затрудняется в объяснении своих действий;

• 0 баллов - справился с задачей после применения приема припоминания, давал сбивчивые односложные ответы на наводящие вопросы, сделал более трех ошибок (педагогом предъявлялась вспомогательная картинка, и задавались наводящие вопросы). Нет связного описания действий, объяснение отсутствует.

Данная 4-х бальная система оценки позволила наиболее точно отнести развитие математических способностей ребенка к тому или иному уровню развития.

Из обработанных данных видна положительная динамика развития логического мышления у детей. Однако, учитывая то, что в группе имелись дети с усложненным диагнозом (не только речевого развития, но и поведенческих нарушений), у 2 детей отмечен низкий уровень развития. Дети усвоили материал, однако действия репродуктивного характера, ребенок не проявляет творчества, затрудняется в объяснении.

Уровни	Обследование на начальном этапе	Обследование на заключительном этапе	Примечание (положительность результата
	25	25
Высокий	0%	42%	Увеличилось количество детей на 42%
Средний	33%	42%	Увеличилось количество детей на 9%
Низкий	67%	16%	Уменьшилось на 51%

На основании вышеизложенного можно сделать вывод: разработанная система занятий математического цикла с использование данных дидактических средств позволила добиться высоких результатов:

• дети овладели приемами выявления и абстрагирования свойств, сравнения, классификации, обобщения, логическими действиями и операциями. У них появилась способность к замещению и моделированию свойств, умению кодировать и декодировать информацию о них.
• с помощью блоков Дьенеша дети овладели знанием о
  цвете, величине, форме и пространственных ориентировках.

Таким образом, предположение о том, что логическое мышление дошкольников характеризуется рядом специфических особенностей, которое можно скорректировать с помощью специально подобранных дидактических игр, включенных в образовательно-воспитательную работу дошкольного образовательного учреждения возможно, если соблюдать следующие условия:

1.     Создание специально подобранной системы занятий, игр-упражнений, игровых заданий с дидактическим содержанием.

2.     Целенаправленное развитие математических способностей должно осуществляться на протяжении всего дошкольного периода.

3.     Совместная деятельность воспитателей, родителей должна быть направлена на развитие математических способностей.

4.     Игры, направленные на формирование математических способностей должны быть разнообразны по содержанию, сложности, использованию наглядности. Необходимо продумать вариативность игр и заданий.

5.     Систему игровых заданий следует включать во все виды детской деятельности.

III. Практическая часть.

Организация учебно-воспитательного процесса

Как уже было сказано выше, на первое место по формированию логического мышления у детей, поставила блоки Дьенеша. Определилась с задачами использования логических блоков на занятиях по математике и в кружке.

1.     Развивать логическое мышление.

2.     Развивать представление о множестве (сравнение, разбиение, классификация)

3. Развивать умение выявлять свойства в объектах, называть их, обозначать объекты по их свойствам, объяснить сходства и различия объектов, обосновать свои рассуждения.

4. Познакомить с формой, цветом, размером, толщиной объектов.

5.Развивать пространственное представление.

6.Развивать знания, умения, навыки для самостоятельного решения учебных и практических задач.

7.Развивать мыслительные процессы, творческие способности, воображение, фантазию, способность к моделированию.

Решение этих задач позволило детям успешно овладеть основами математики.

Вот основные формы организации, которые я использую в работе с логическими блоками:

o    Занятия (комплексные, интегрированные), обеспечивающие наглядность, системность и доступность, смену деятельности.

o    Совместная и самостоятельная игровая деятельность (дидактические игры, настольно – печатные, подвижные, сюжетно – ролевые игры)

o    Вне занятий. Работа в кружке «Геометрическая мозаика», где тоже использую логические блоки в играх. Начинаю с простейших игр, например: «Сделай узор», «Воздушные шары», «Запомни узор», «Найди свой домик», «Пригласительный билет». А затем уже знакомлю с играми, где учу детей читать кодовое обозначение логических блоков: «Разноцветные шары», «Волшебный ключик», «Поле чудес», «Подари кукле бусы», «Цыпленок», «Рыбка», «Найди и разложи по форме», и т.д.

o    Чтобы детям было легче классифицировать фигуры, я изготовила карточки для настольно – печатных игр. Все эти игры можно использовать в любой возрастной группе (усложняя или упрощая задания). Когда я вижу, что ребята немного научились выполнять задания, познакомились с кодовыми обозначениями, начинаю использовать логические блоки на заданиях по математике. Для того чтобы поддержать интерес детей к занятиям к обучению, использую разноцветные игровые задачи. В этом возрасте детей привлекают занятия, где есть сюжет, много интересных сказочных персонажей.

o    Занятия, где я использую логические блоки, помогают при изучении нового материала, а также для его закрепления. При знакомстве с геометрическими фигурами предлагаю такие занятия: «Путешествие в город геометрических фигур», «Путешествие по стране «Смекалочка», «Увлекательное путешествие по сказке «Маша и Медведь» с использованием игровых упражнений с блоками Дьенеша», «Сказочное путешествие с Иваном-Царевичем за тридевять земель», «Страна Математика» и др. Во всех этих конспектах использованы блоки Дьенеша.

o    Использование логических блоков в рисовании, конструировании и моделировании предметов из геометрических фигур разнообразит занятия детей, делает их интересными, помогает легче ориентироваться в пространстве и закономерностях.

Все занятия по логическому мышлению я внесла в тематический план работы по математике на учебный год.

Для более успешного обучения математике (по блокам Дьенеша), привлекаю родителей, используя разнообразные формы работы с ними:

• Консультация о подборе игр по формированию логического мышления;
• Индивидуальные беседы с рекомендациями по каждому конкретному ребенку;
• Собрания с показом фрагментов занятий (цель – обратить внимание родителей на коммуникативную, речевую и мыслительную стороны развития их ребенка);
• Совместные игры – занятия с детьми и родителями (во второй половине дня кружковая работа);
• Праздники, совместные досуги, участие родителей в конкурсах, выставках,соревнованиях между командами родителей и детей (используется занимательный материал, логические блоки Дьенеша);
• Совместный выбор и приобретение дидактических и развивающих игр;
• Подбор и демонстрация специальной литературы, направленной на развитие логического мышления;

Результативность работы

Анализ работы показал, что родители стали понимать значение развития логического мышления у детей, его связь с развитием интеллектуальных способностей и речи. Уровень заинтересованности родителей в использовании игр на основе логических блоков Дьенеша несомненно вырос. Так, в 2010г.- 18%;в 2011г.- 36%; в 2012г.- 67%.

IV. Заключение

Результаты опыта

Анализ работы с дошкольниками показал, что у детей сформированы такие первичные понятия, как логические действия, кодировка информации, структура и алгоритмы выполнения действий. Дети умеют не только думать, следить за координацией движений, но и использовать более сложные грамматические структуры предложений в речи на основе сравнений и сочетаний однородных предметов, строить высказывания с союзами «и», «или», понимать суть отрицания и частицы «не».

Мониторинг развития логического мышления у детей старшего дошкольного возраста группы «Семицветик» при формировании математических способностей.

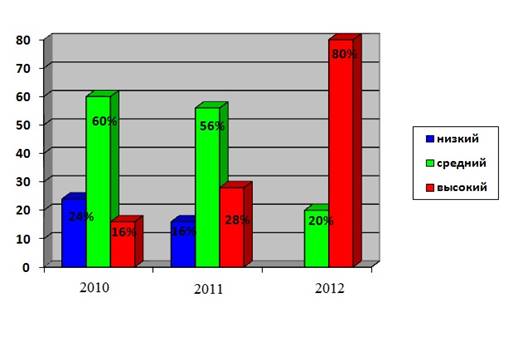
Вывод: из результатов мониторинга можно судить об эффективности проведенной работы

в 2010г.- сформированность первичных понятий, как логические действия, кодировка информации, структура и алгоритмы выполнения действий, дети показали следующие результаты:

из 25 общего количества детей

высокий уровень развития показали 4 воспитанника, что составило 16 %

средний уровень развития показали 15 воспитанников, что составило 60 %

низкий уровень развития показали 6 воспитанников, что составило 24 %

в 2011г.- промежуточный, в начале использования логических блоков Дьенеша и различных форм работы с ними воспитанники показали следующие результаты:

из 25 общего количества детей

высокий уровень развития показали 7 воспитанников, что составило 28 %

средний уровень развития показали 14 воспитанников, что составило 56 %

низкий уровень развития показали 4 воспитанника, что составило 16 %

в 2012г.- в завершении работы, создание специально подобранной системы занятий, игр-упражнений, игровых заданий с дидактическим содержанием воспитанники показали следующие результаты:

из 25 общего количества детей

высокий уровень развития показали 5 воспитанников, что составило 20 %

средний уровень развития показали 20 воспитанников, что составило 80 %

Наблюдая за ростом мыслительной и речевой деятельности, которая очевидна при многоразовом использовании логических операций, утверждаю, что:

• Дети ознакомились с приемом сравнения, анализа, синтеза, классификации. Могут установить определенную последовательность некоторых событий.
• Примерно ⅓ детей испытывает устойчивый интерес к развивающим играм.
• Возросла степень их активности в самостоятельной деятельности. Работа по развитию мышления дошкольников при использовании блоков Дьенеша принесла свои плоды.
• Дети с легкостью усвоили знания о геометрических фигурах, научились различать предметы по форме, цвету, размеру, толщине.
• Заметно развились мыслительные процессы, способность к моделированию и замещению свойств, умение кодировать и декодировать информацию.
• Дети делают первые шаги по высказыванию суждения, доказательства. Это достаточно сложная речевая деятельность, но она очень необходима.
• Ребенок умеет объяснять свою позицию, выразить свое мнение и не стесняется этого.
• Дошкольники, которые логически мыслят стали более раскрепощёнными: у них хорошо развиты познавательные процессы и мыслительные операции, они составляют алгоритмы, кодируют и декодируют информацию, обобщают предметы по одному, двум, трем сходствам и различиям.
• Все это послужит успешной подготовке их к школе.

Таким образом, система работы по развитию логического мышления дошкольников с использованием логических блоков Дьенеша способствует более успешному формированию у детей основных приёмов логического мышления.

Адресная направленность опыта.

Опыт моей работы показал эффективность использования логических блоков как

игрового материала в работе с детьми дошкольного возраста для:

• Ознакомления детей с геометрическими фигурами и формой предметов, размером;

• Развития мыслительных умений: сравнивать, анализировать, классифицировать, обобщать, абстрагировать, кодировать и декодировать информацию;

• Усвоения элементарных навыков алгоритмической культуры мышления;

• Развития познавательных процессов восприятия памяти, внимания, воображения;

• Развития творческих способностей.

Блоки Дьенеша - универсальный дидактический материал, позволяющий успешно реализовывать задачи познавательного развития детей, поставленные в программах "Детство", "Развитие", "Радуга", "Истоки" и других.

Рекомендую использовать опыт моей работы с блоками Дьенеша педагогам коррекционных, разновозрастных группах, а также, в группах кратковременного пребывания.

Эти материалы необходимы всем педагогам, использующим в своей работе игры и

упражнения с блоками Дьенеша. В описании раскрыты возможности использования их не только как дополнительного материала к блокам Дьенеша, но и для самостоятельных игр, а также показаны возможные пути придумывания игр с детьми.

 

Скачано с www.znanio.ru