Проект по математике "Устный счёт-легко и просто".

МКОУ Баклушевская СОШ им.Е.М.Дергай

Доволенского района Новосибирской области

Быстрый счет – легко и просто

Работу выполнил учащийся 6 класса

Нуралинов Дамир

рук: Третьякова Лидия Николаевна

учитель математики

2017-2018 у.г

Введение

Введение

Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Освоение вычислительных навыков развивает память и помогает усваивать предметы естественно-математического цикла. Существует много приемов упрощения арифметических действий. Знание упрощенных приемов вычисления особенно важно в тех случаях, когда вычисляющий не имеет в своем распоряжении таблиц и калькулятора. Мы хотим остановиться на способах сложения, вычитания, умножения, деления, для производства которых достаточно устного счета или применения ручки и бумаги. Мотивацией для выбора темы послужило желание продолжения формирования вычислительных навыков, умения быстро и чётко находить результат математических действий. Правила и приёмы вычислений не зависят от того, выполняются они письменно или устно. Однако владение навыками устных вычислений представляет большую ценность не потому, что в быту ими пользуются чаще, чем письменными выкладками. Это важно ещё и потому, что они ускоряют письменные вычисления, приобретают опыт рациональных вычислений, дают выигрыш в вычислительной работе. На уроках математики приходится, много делать устных вычислений и когда учитель показал нам приём быстрого умножения на числа 11, у нас возникла идея, а существуют ли ещё приёмы быстрого вычисления. Мы поставили перед собой задачу, найти и опробовать другие приёмы быстрого вычисления. Немногие умеют считать быстро и правильно. Исследование, проведенное в нашей школе, показало: 1. Зачем нужно уметь считать? а) пригодится в жизни, например, считать деньги; б) чтобы хорошо учиться в школе; (16%) в) чтобы быстро решать:г) чтобы быть грамотным; д) не обязательно уметь считать. 2. Перечислите, при изучении, каких школьных предметов тебе понадобится правильно считать? а) математика; б) технология; в) музыка; 3. Знаешь ли ты приемы быстрого счета? а) да, много; б) да, несколько; в) нет, не знаю. 4. Применяешь ли ты при вычислениях приемы быстрого счета? а) да; б) нет 5. Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать? а) да; б) нет Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро, считать в уме можно только при большом желании и систематической тренировке в решении задач.

Цель:  научиться приемам быстрого счета.

Задачи:

1.Найти и обработать материал по данной теме.

2.Провести анкету в разных классах школы.

3.Узнать: как считали в разные времена.

4. Создать текстовый документ.

5.Создать презентацию.

6.Защитить проект

"Компьютер" каменного века

Даже не зная чисел, люди уже пытались считать. Если нашим предкам, обитавшим в пещерах и носившим шкуры, нужно было поменяться чем-либо с соседним племенем, они поступали просто: расчищали площадку и выкладывали, например, наконечник стрелы. Рядом ложилась рыба или горсть орехов. И так до тех пор, пока не заканчивался один из обменных товаров, или глава "торговой миссии" не решал, что уже хватит. Примитивно, но по-своему очень удобно: и не запутаешься, и не обманут.

С освоением скотоводства задачи усложнились. Большое стадо нужно было как-то считать, чтобы знать, все ли козы или коровы на месте. "Счетной машиной" неграмотных, но умных пастухов стала долбленая тыква с камешками. Как только животное покидало загон, пастух клал в тыкву камешек. Вечером стадо возвращалось, и пастух вынимал по камешку с каждым входившим в загон животным. Если тыква пустела, он знал, что со стадом все в порядке. Если оставались камешки - шел искать потерю.

Когда появились цифры, дело пошло веселее. Хотя еще долго у наших предков в ходу было лишь три числительных: "один", "пара" и "много".

Простейшие приемы вычитания и сложения

Двухзначные числа складываются легко. Если во втором слагаемом последняя цифра больше пяти, число округляется до следующего десятка, а потом "лишнее" вычитается. 22 + 47 = 22 + 50 - 3 = 69. Если ключевая цифра меньше пятерки, то надо сложить сперва десятки, затем единицы: 27 + 51 = 20 + 50 + 7 + 1 = 78.

С трехзначными числами точно так же не возникает никаких трудностей. Складываем их, как читаем, слева на право: 321 + 543 = 300 + 500 + 20 + 40 + 1 + 3 = 864. Гораздо проще, чем в столбик. И гораздо быстрее.

А вычитание? Принцип тот же: вычитаемое округляем до целого и добавляем недостающее: 57 - 8 = 57 - 10 + 2 = 49; 43 - 27 = 43 - 30 + 3 = 16. Быстрее чем на калькуляторе - и никаких претензий от учителя даже во время контрольной!.

Вычитание из 1000

Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:

1000-648

Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352

Умножение на 9

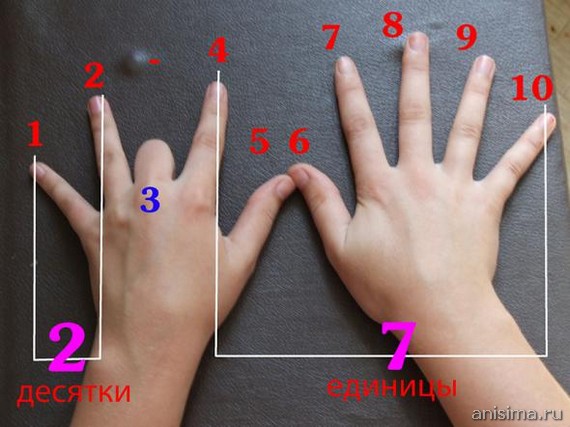
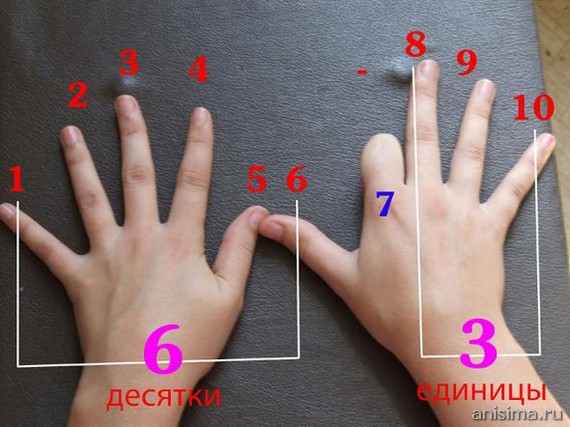
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует числу на которое умножаем  числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

Умножение двузначного числа на 11. 

При умножении двузначного числа на 11 цифры этого числа раздвигают и в середину ставят сумму этих цифр.

Например:

а) 35 ⋅ 11 = 385, т. к. 3 + 5 = 8

б) 68 ⋅ 11 = 748, т.к. 6 + 8 = 14 то число десятков будет равно 4, а цифра сотен увеличится на единицу и будет равна 7.

УМНОЖЕНИЕ ЧИСЕЛ ОТ 10 ДО 20

Можно очень просто умножать такие числа. К одному из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел. Пример 1. 16∙18=(16+8) ∙ 10+6 ∙ 8=288, или Пример 2. 17 ∙ 17=(17+7) ∙ 10+7 ∙ 7=289. Задание: Умножьте быстро 19 ∙ 13. Ответ 19 ∙13=(19+3) ∙10 +9 ∙3=247.

Умножение десятичной дроби на 11.

Умножаем, не обращая внимания на запятую, а затем в полученном результате отделяем справа запятой столько цифр, сколько их стояло после запятых в обоих множителях вместе.

Например:

а) 4, 7 ⋅ 0,11 = 0,517, т. к. 47 ⋅ 11 = 517 и отделяем запятой справа 3 цифры (1 + 2)

в) 0,062 ⋅ 1100 = 68,2. Умножили 62 на 11, получили 682, приписали 2 нуля, получилось 68200 и отделили справа запятой 3 цифры. Получилось 68,200 = 68,2

УМНОЖЕНИЕ НА 22, 33, ..., 99.

Чтобы двузначное число умножить на 22, 33, ..., 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 = 4 11; 55 = 5 ∙ 11 и т.д. Затем произведение первых чисел умножить на 11. Пример 1. 24 ∙ 22 = 24 ∙ 2 ∙ 11 = 48 ∙ 11 = 528 Пример 2. 23 ∙ 33 = 23 ∙ 3 ∙ 11= 69 ∙ 11 = 759 Задание: Умножьте 18∙ 44 5. УМНОЖЕНИЕ НА 5, НА 50, НА 25, НА 125 При умножении на эти числа можно воспользоваться следующими выражениями: a ∙ 5=a ∙ 10:2 a ∙ 50=a ∙ 100:2 a ∙ 25=a ∙ 100:4 а ∙ 125=а ∙ 1000:8 Пример1. 17 ∙ 5=17 ∙ 10:2=170:2=85 Пример 2. 43 ∙ 50=43 ∙ 100:2=4300:2=2150 Пример 3. 27 ∙ 25=27 ∙ 100:4=2700:4=675 Пример 4. 96 ∙ 125=96:8 ∙ 1000=12 ∙ 1000=12000 Задание: умножьте 824∙25.

Способы быстрого деления

. ДЕЛЕНИЕ НА 5, НА 50, НА 25 При делении на 5, на 50, на 25 можно воспользоваться следующими выражениями: a:5= a ∙ 2:10 a:50=a ∙ 2:100 a:25=a ∙ 4:100 Примеры: 35:5=35 ∙ 2:10=70:10=7 3750:50=3750 ∙ 2:100=7500:100=75 6400:25=6400 ∙ 4:100=25600:100=256 &3.

Способы быстрого сложения и вычитания натуральных чисел.

- Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо вычесть столько же единиц. Пример. 785+963=785+(963+7)-7=785+970-7= 1748 - Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на столько же единиц, то сумма не изменится. Пример. 762+639=(762+8)+(639-8)=770 + 631=1401 - Если вычитаемое уменьшить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится. Пример. 529-435=(529-5)-(435+5)=524-440=84,

Фокусы в математике

Любимая цифра.

Предложите  теперь выполните умножение (на калькуляторе) числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то умножить нужно на 35. Получится произведение, записанное только любимой цифрой.

Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45.

Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.

Угадать возраст.

Умножаем число своих лет на 10, затем любое однозначное число умножить на 9,  из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.

Всегда девятка

Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке. Затем вычесть меньшее из большего. Когда зритель это сделает, скажите ему, что в середине числа стоит девятка.

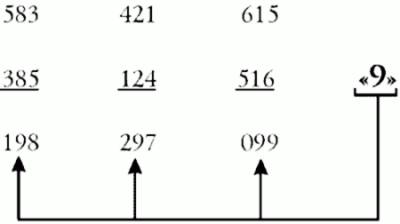
Секрет фокуса: Вы будете правы, потому что девятка всегда будет в середине независимо от того, какие цифры написаны.

"Зарядка" для ума

Приемы быстрого счета способны здорово облегчить жизнь и ребенку в школе, и маме в магазине или на кухне, и папе на производстве или в офисе. Но мы предпочитаем калькулятор. Почему? Не любим напрягаться. Нам тяжело держать числа, даже двухзначные, в голове. Почему-то не держатся.

Попробуйте выйти на середину комнаты и сесть на шпагат. Почему-то "не сажается", да? А гимнаст делает это совершенно спокойно, не напрягаясь. Тренироваться нужно!

Самый простой способ тренировки и, одновременно, разминки мозга: устный счет вслух (обязательно!) через число до ста и обратно. Утром, стоя под душем, или готовя завтрак, посчитайте: 2.. 4.. 6.. 100... 98.. 96. Можно считать через три, через восемь - главное, делать это вслух. Всего через пару недель регулярных занятий вы удивитесь, насколько ПРОЩЕ станет обращаться с числами.

Источники

http://anisim.org/articles/priemy-bystrogo-scheta-bez-kalkulyatora/

http://yun.moluch.ru/archive/9/633/

http://www.calculator888.ru/blog/matematika/ustnyi-schet.html

Скачано с www.znanio.ru