Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 15 имени Героя Советского Союза Виктора Иосифовича Костина хутора Средний Челбас

муниципального образования Павловский район

 

 

 

 

 

ИТОГОВАЯ ИНДИВИДУАЛЬНАЯ ПРОЕКТНАЯ  РАБОТА

 

 

НАИМЕНОВАНИЕ ТЕМЫ

 

 

«Всемирное умножение»

 

 

 

 

 

 

 

Выполнила Толмачева Екатерина Романовна ученица 10 «А» класса Научный руководитель: Штейзель Александра Николаевна учитель математики

 

 

 

                                                      

 

 

 

2021 -2022 учебный год

Оглавление

Введение. 3

Основная часть. 5

История появление таблицы умножения. 5

Пифагор и таблица умножения. 6

Виды умножения: 8

Умножение на 11. 8

Умножение на 12. 8

Умножение на 101 и 111. 8

Умножение на 5, 25, 125. 9

Простое умножение чисел близких к 100. 9

Умножение методом Ферроля. 9

Способы умножения. 9

Русский способ умножения. 9

Китайско-японский способ умножения. 10

Итальянский способ умножения. 12

Немецкий способ умножения. 12

Практическая часть. 14

Заключение. 16

 

 

Введение

Во все времена математика была и остается одним из основных предметов в школе, потому что математические знания необходимы всем людям. Математика развивает способность к логическому мышлению, что позволяет человеку жить интересно и никогда не скучать. Эта прекрасная наука развивает умение мыслить нестандартно, находить выход из любых ситуаций.

В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление.

Такие навыки помогут человеку в учёбе, в быту, в профессиональной деятельности. Проанализировав много информации, я открыла для себя очень интересные и необычные способы быстрого умножения.

Актуальность: мне нравится проводить различные вычисления, но обычный способ умножения бывает слишком тяжелым и долгим. Также умении быстро считать поможем мне при сдачи ЕГЭ.

Гипотеза: современные школьники знают о способах быстрого умножения, но не используют их на практике.

Цель: изучить методы быстрого счета

Задачи:

1.Познакомиться с историей создания счёта;

2.Изучить способы быстрого умножения;

3.Научиться умножать числа легко, быстро и удобно;

4. Выяснить знают ли современные школьники о способах быстрого умножения;

5. Составить буклет по выполнению умножения нестандартными способами.

Объект: математическое действие умножение.

Предмет: нестандартные способы умножения.

Продукт проекта: буклет «Способы быстрого умножения».

Практическая значимость работы: расширение математического кругозора. Возможность использования материалов исследования во внеклассных мероприятиях и в быту.

Основная часть

История появление таблицы умножения

Нельзя точно ответить кто именно положил начало арифметике. Но можно точно сказать, что умножать люди начали значительно позже, чем складывать. Египтяне выполняли умножение посредством повторного сложения или последовательного удвоения. В Вавилоне при умножении чисел пользовались специальными таблицами умножения-«предками» современных.

В древней Индии применяли способ умножения чисел, тоже довольно близкий к современному. Люди, живущие в Индии, производили умножение чисел, начиная с высших разрядов. При этом они стирали те цифры, которые при последующих действиях надо было заменять, так как к ним прибавляли число, ныне запоминаемое нами при умножении. Таким образом, математики Индии сразу записывали произведение, выполняя промежуточные вычисления на песке или в уме. Таблица в Индии включает в себя числа до 20-ти. Индийский прием умножения перешел к арабам. Но арабы не стирали цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой.

В Европе продолжительное время произведение называли сумма умножения. Название «множитель» упоминается в работах VI века, а «множимое» - в XIII веке. В XVII веке некоторые из математиков стали обозначать умножение косым крестиком, а иные употребляли точку. Только в конце XVIII века большинство математиков стали употреблять в качестве знака умножения точку, но допускали и употребление косого креста. Знаки умножения и знак равенства стали общепризнанными благодаря авторитету знаменитого немецкого математика Готфрида Вильгельма Лейбница (1646-1716)

Известно, что впервые таблица умножения была введена в школах в средневековой Англии. Выглядела она как система перемножения чисел до 12. В Англии до сих пор сохранился именно такой средневековый вариант по той причине, что в жизни англичан часто приходится умножать именно на 12. Таким образом, мы видим, что таблица не во всех странах одинакова.

Интересно, что на Руси существовал крестьянский способ умножения, который заключался в том, что первый множитель увеличивается в два раза, а второй уменьшался тоже в два раза. И эта операция продолжалась до тех пор, пока второй множитель не становился равен одному. Строки, в которых правое число четное, удалялись, а сумма левых чисел и оставшихся строк давали нужный результат.

Пифагор и таблица умножения

Привычная для нас таблица умножения — это 8 столбцов с последовательными примерами на задней обложке тетради. Таблицу умножения также называют «Таблицей Пифагора», особенно когда она представлена в виде квадрата, стороны которого — множители, а в ячейках стоит их произведение. Именно так принято считать в европейской культуре. При этом существует очень интересный факт: не обнаружено ни одного письменного свидетельства тому, что именно Пифагору принадлежит авторство таблицы. Существуют только косвенные доказательства.

Последователь его учения — Никомах Герасский, который жил на рубеже I и II веков нашей эры, записал таблицу в привычном нам виде в своем сочинении «Введение в арифметику». Именно он утверждал, что авторство принадлежит древнегреческому ученому Пифагору.  Мнения ученых по поводу авторства таблицы умножения разделились. И многие считают, что Пифагор не может быть ее создателем, ведь существуют факты, подтверждающие другое ее происхождение.

Самая старая десятичная таблица умножения найдена на раскопках древних китайских городов. Ученые датируют ее 305 г. до н.э., т.е. она существенно старше, чем сам Пифагор и его труды. При раскопках японского города Нара нашли дощечку с фрагментами записей, которые подтверждают, что в древней Японии вели подсчеты с помощью таблицы. Интересно то, что иероглифы похожи на древнекитайское письмо.

Это не единичный случай обнаружения подобных табличек археологами. Подобную дощечку нашли на раскопках еще одной японской столицы Хэйнан. Таким образом, ученые предполагают, что таблица умножения могла попасть из Китая в Японию, так как между двумя империями были очень прочные торговые отношения. По мнению ученых, таблица умножения, которую придумали в Китае, могла попасть в Индию вместе с торговыми караванами, а затем уже распространиться по Азии и Европе.

Но есть и еще одна версия, исходя из которой таблица была изобретена в Месопотамии. Эта теория тоже подтверждается находками археологов. Самая старейшая табличка была найдена на раскопках древнего Вавилона и имеет возраст около 4000 лет.

В 493 году появился новый вариант, предложенный ученым Викторием Аквитанским: он записал таблицу из 98 столбцов, которая представляла в римских числах результат перемножения чисел от 2 до 50.

В 1820-м году шотландский физик и профессор математики Джон Лесли в своей книге «Философия арифметики» опубликовал таблицу умножения до 99. Он же стал тем, кто начал давать своим ученикам рекомендации заучить ее.

В Россию современная таблица умножения попала благодаря математику Леонтию Филипповичу Магницкому, который в 1707 году издал первый учебник по математике под названием «Арифметика». В этом учебнике были таблицы сложения и умножения. Такое нововведение, как заучивание таблицы умножения было поистине революционным. Оно значительно облегчало повседневные расчеты, так как другие хитрые способы вычисления приводили к тому, что увеличивалось количество ошибок и замедлялся процесс подсчета.

 

 

 

Виды умножения:

Умножение на 11

Чтобы умножить на 11 число, сумма  цифр которого равна 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр.

Например: 34 х 11=3(3+4)4=374;

Чтобы умножить на 11 число, сумма которого больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

Например: 56 х 11=5(5+6)6=5(11)6=616

Умножение на 12

Чтобы умножить на 12 число, надо:

1) Последнюю цифру множимого удваиваем и записываем как самую правую цифру результата;

2) Каждую следующую цифру множимого удваиваем, складываем со своим правым соседом и записываем в результат (если ответ содержит больше одной цифры, то просто переносим 1 или 2 в следующий разряд);

3)                Первую цифру множимого ставим самой левой цифрой результата

Например: 126 х 12=1512

6 х 2=12; 2 х 2+6+1=11; 1 х 2+2+1=5

Умножение на 101 и 111

Умножение двузначного числа на 101. Чтобы умножить двузначное число на 101, надо рядом записать полное число два раза.

Например: 49 х 101 = 4949

Умножение двузначного числа с суммой цифр, меньшей 10, на 111.

Находим сумму цифр данного двузначного числа (4 + 2 = 6). Раздвигая цифры множимого, дважды пишем между ними сумму цифр данного двузначного числа.

Например: 81 х 111 =8991

Умножение на 5, 25, 125

Чтобы умножить число на 5, 25, 125, достаточно разделить его соответственно на 2, 4, 8, и после умножить на 10, 100, 1000.

Например: 1486 х 5 = 7430, так как 1486 : 2 = 743

2784 х 25 = 69600, так как 2784 : 4 = 696

4896 х 125 = 612000, так как 4896 : 8 = 612

Простое умножение чисел близких к 100

Например, нужно перемножить 94 на 98.

Для начала нужно найти вспомогательные числа. Их находим вычитанием доступного нам числа от 100. В нашем случаи получается, что вспомогательные числа это 6 и 2.

Далее нужно сложить 6 и 2, а затем получившееся число отнять от 100. Получается 6+2=8, 100-8=92. Значит в начале нашего числа стоит цифра 92.

Чтобы найти последние цифры необходимо перемножить 6 и 2, получается 12. В итоге у нас получилось, что 94 х 98 =9212.

Умножение методом Ферроля

Для умножения единиц произведения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.

14 х 17=238

4 х 7=28, пишем 8 и запоминаем 2, далее 4 х 1+ 7 х 1= 11+2=13, пишем 3 и 1 запоминаем, потом 1 х 1=1+1=2. Получаем 238.

Способы умножения

Русский способ умножения

Способ этот, был употребителен в обиходе русских крестьян и унаследован ими от глубокой древности. Сущность его заключается в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа, таблица умножения в этом деле без надобности.

Деление пополам продолжают до тех пор, пока в частном не получится 1, при этом параллельно удваивают другое число. Последнее удвоенное число и даёт искомый результат. Нетрудно понять, на чём этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение.

Например: 24 х 4=96

Правильность приёма станет ясна, если принять во внимание, что:

5 × 48 = (4 + 1) × 48 = 4 × 48 + 48

21 × 12 = (20 + 1) × 12 = 20 × 12 + 12

Ясно, что числа 48, 12, утрачиваемые при делении нечётного числа пополам, необходимо прибавить к результату последнего умножения, чтобы получить произведение. Русский способ умножения и элегантен и экстравагантен одновременно.

Китайско-японский способ умножения

В Китае давно существует свои метод перемножение чисел, отличный от привычного для нас. Он позволяет легко и быстро перемножать двух- или трехзначные числа с помощью нехитрой схематической таблицы, которую может изобразить даже школьник младших классов.

Как же китайцы умножают числа? Давайте разберемся!

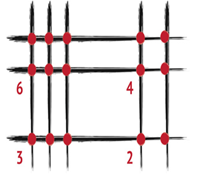
Возьмём числа 21 и 32. Для этого надо нарисовать эти числа при помощи горизонтальных и вертикальных прямых

Шаг 1. Сначала рисуем первый множитель — 21. В нём 2 десятка и 1 единица, значит, рисуем горизонтально 2 параллельные прямые (сверху) и 1 прямую (снизу).

Шаг 2. Поверх первого множителя теперь рисуем второй множитель — 32. В нём 3 десятка и 2 единицы, значит, рисуем вертикально 3 параллельные прямые (слева) и 2 параллельные прямые (справа). Эти вертикальные прямые будут пересекать горизонтальные прямые первого множителя. Получился рисунок, похожий на всем известный знак «решётка».

Шаг 3. Далее смотрим на рисунок и считаем, сколько точек пересечения имеют горизонтальные и вертикальные прямые в каждом углу «решётки».

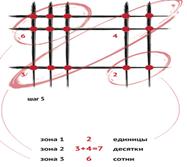
Шаг 4. Делим эти точки на три зоны (части).

Шаг 5. Ответ (т. е. произведение этих двух множителей) «собираем» по порядку, двигаясь от первой зоны ко второй, затем к третьей. При этом необходимо запомнить, что число из первой зоны соответствует единицам, число из второй зоны — десяткам, число из третьей зоны — сотням искомого произведения.

1)    2)

3)       4)

Итальянский способ умножения

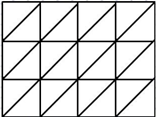
Итальянский способ умножения или способ умножения «Сеткой». В Италии, а также во многих странах Востока, этот способ приобрел большую известность.

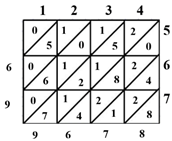
Например: умножим 1234 на 576.

1) Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.

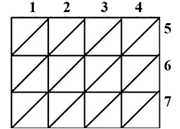
2)Умножаем число каждого ряда последовательно на числа каждой колонки.

Т.е. 4 х 5 = 20. Записываем 2 и 0.

1х 5 * 3 = 6. Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.

3) Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.

1)     2) 3)

 

Немецкий способ умножения

Самый известный и применяемый способ в Российском образовании придумал немецкий педагог-математик Адам Ризе. Чтобы перемножить два числа, записываем большее над меньшем. Затем начиная с единиц и двигаясь к высшим разрядам умножаем поочерёдно каждую цифру нижнего числа на верхнее. Если при умножении цифр получаем число большее десяти, добавляем единицу к следующему разряду.

 

Практическая часть

Для того чтобы узнать, что думают люди по поводу умножения и каким методом большинство умножают числа, мы составили анкету (см. Приложение 1) и провели анкетирование.

В опросе участвовало 20 человек, ученики 8-10 классов. Результаты анкетирования приведены в таблицах (Приложение 2).

 

 

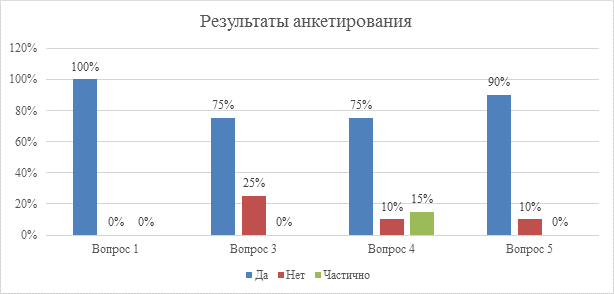
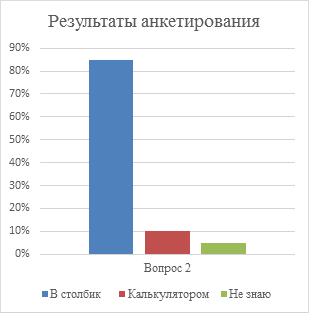
На основе данных диаграмм можно сделать вывод, что 100% опрошенные считают, что современному человеку необходимо умение быстро считать. Хотя методов умножения великое разнообразие, но большинство (85%) ответило, что умножали бы трехзначные числа в столбик. Также на вопрос «Знаете ли вы как легко умножать двухзначные числа на 11?» 75% опрошенных ответили, что не знаю, что было очень удивительно. Также в ходе анкетирования мы выяснили, что всего 10% не знают о быстрых методах умножения и 90% хотели бы научится быстро и просто считать, что подтверждает актуальность моего проекта.

         После проведенного исследования мы разработали буклет (Приложение 3).

 

                                             Заключение

В истории математики есть много интересных событий и открытий, но, к сожалению, не вся эта информация доходит до нас, современных учеников.

         Из всех найденных мною необычных способов умножения многозначных чисел более интересным показался итальянский способ. Недостаток этого способа заключается в построении прямоугольной таблицы, которая занимает некоторое время.

Самым простым мне показался русский способ умножения, который использовали крестьяне. Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).

Китайско-японский способ - самый наглядный способ умножения. Умножая числа таким способом, вовсе не обязательно знать таблицу умножения. Надо всего лишь правильно начертить линии, сосчитать количество пересечений и вывести результат.

         Считаем, что цель нашей работы достигнута, задачи полностью выполнены. Вовремя исследования подтвердилось, что большинство знают, что есть способы быстрого умножения, но на практике используют традиционный метод вычисления (в столбик).

 

Список использованной литературы:

1)    https://oyla.xyz/article/umnozenie-po-kitajsk

2)    https://tablica-umnozhenia.ru/stati/istoriya-sozdaniya-tablitsy-umnozheniya-2

3)    https://zen.yandex.ru/media/haknem_shkola/maloizvestnye-sposoby-ustnogo-umnojeniia-mnogoznachnyh-chisel-na-5-25-i-125-607189dd420d4500ed1d2c1d

4)    https://zen.yandex.ru/media/haknem_shkola/maloizvestnye-sposoby-ustnogo-umnojeniia-mnogoznachnyh-chisel-na-5-25-i-125-607189dd420d4500ed1d2c1d

5)     

Приложения:

Приложение 1

Анкета

1) Нужно ли современному человеку умение быстро считать?

 

2) Каким методом ты будешь умножать трёхзначные цифры?

 

3) Знаете ли вы как легко умножить двухзначные число на 11?

 

 

5) Хотели бы вы научиться быстро и просто считать?

 

Приложение 2

 

	1 в.	3 в.	4 в.	5 в.
Да	20 от. (100%)	15 от. (75%)	15 от. (75%)	18 от. (90%)
Нет	0 от. (0%)	5 от. (25%)	2 от. (10%)	2 от. (10%)
Частично	0 от. (0%)	0 от. (0%)	3 от. (15%)	0 от. (0%)

 

Вопрос 2

Варианты ответов	Процентное соотношение, %
В столбик	17 от. (85%)
Калькулятором	2 от. (10%)
Не знаю	1 от. (5%)

 

 

Скачано с www.znanio.ru