Программа факультативного курса по математике для 9 класса "Проценты в современной жизни"

 

 

                    

 

Программа

факультативного курса по математике для 9 класса

 «Проценты в современной жизни»

 

Автор разработки:

Назарова Маргарита  Алексеевна,

 учитель математики

                                                                                          первой квалификационной категории

                                                                           МБОУ «Гимназия №3»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г. Чистополь – 2018 г.

 

Оглавление

 

1. Пояснительная записка……………………………………………....3-6       
2. Содержание программы…………………………………………......7-9
3. Учебно-методическое обеспечение.

Перечень рекомендованной литературы  для учителя…..……........10

      Перечень рекомендованной литературы для учащихся…………...10

      Интернет-ресурсы…………………………………………………….10

4. Учебно-тематический план………………………………………..11-13
5. Краткое описание занятий……………………………………………14.
6. Приложения:

          Материалы для проведения практикумов, уроков текущего  и     итогового контроля.................................................................................     25-32

      Мониторинг……………………………………………………………

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пояснительная записка

Программа является предметно-ориенти­рованной и предназначена на год обучения для реализации в 9 классе общеобразовательной школы для расширения теоретических и практический знаний учащихся.

Данный факультативный курс посвящён одной из важнейших тем математики «Процентные исчисления». В рамках общеобразовательной школы процентам уделяется несправедливо мало учебного времени, а, следовательно, уровень знаний, необходимый для приобретения умений, навыков для свободного оперирования ими на уроках математики, химии, физики и просто в быту, оказывается недостаточным. Проценты изучаются на первом этапе основной школы, когда учащиеся в силу возрастных особенностей ещё не могут получить полноценные представления о процентах, об их роли в повседневной жизни.

Понимание процентов и умение производить процентные расчёты необходимы каждому человеку; прикладное значение этой темы велико и затрагивает финансовую, демографическую, экологическую, социологическую и другие стороны нашей жизни.

Поэтому представляется необходимым возвращение к процентам на старшей ступени.

Факультативный курс направлен на удовлетворение познавательных интересов учащихся, имеет прикладное общеобразовательное значение, способствует развитию логического мышления учащихся, использует целый ряд межпредметных связей.

    Предлагаемый курс демонстрирует учащимся применение математического аппарата к решению повседневных бытовых проблем каждого  человека, вопросов рыночной экономики и задач технологии производства.  Данный курс должен позволить учащемуся не столько приобрести знания, сколько овладеть различными способами познавательной деятельности.  В каждом разделе курса имеются задания на актуализацию и систематизацию знаний учащихся, задачи различного уровня сложности, сюжеты подавляющего большинства которых, в отличие от обычных искусственных текстовых задач, непосредственно взяты из действительности, окружающей современного человека, в том числе и старшеклассника, - финансовая сфера (платежи, налоги, прибыли), демография, экология, социологические опросы и пр. Уровень сложности задач варьируется от простых упражнений  на применение изучаемых формул до достаточно трудных примеров расчёта процентов в реальных банковских ситуациях.

Тема «Проценты» является универсальной в том смысле, что она связывает между собой многие точные и естественные науки. У учащихся воспитывается чувство удовлетворения от установленной им возможности приложения математики к другим наукам. Они увидят, что такие, на первый взгляд, «бесполезные» вопросы, как сумма членов  арифметической или геометрической прогрессии, имеют глубокий экономический смысл.

Этот курс направлен на то, чтобы вооружить желающих дополнительными знаниями по процентным исчислениям для использования их не только в учебно-познавательном процессе, но и в повседневной жизни – при расчёте выгодности банковской сделки, рентабельности бизнеса, коммерческого предложения.

Содержание курса способствует решению задач самоопределения ученика в его дальнейшей профессиональной деятельности.

Цели факультатива:

·         сформировать понимание  необходимости  знаний процентных вычислений  для решения большого круга  задач , показав широту  применения  процентных расчетов  в реальной жизни

·         способствовать интеллектуальному  развитию обучающихся ,  формированию качеств мышления , характерных для математической деятельности и необходимых   человеку  для жизни в современном  обществе, для общей  социальной ориентации  и решения  практических проблем.

Задачи факультатива:

·         актуализировать ранее изученный и новый материал для обеспечения ученикам достаточно высокого уровня компетентности по этой теме;

·         сформировать умение производить  процентные вычисления  , необходимые  для применения  в практической  деятельности

·         решать основные задачи  на проценты , применять  формулу  сложных процентов

·         привить  обучающимся  основы экономической  грамотности

·         помочь обучающемуся  оценить  свой потенциал  с точки зрения образовательной  перспективы

Факультатив обеспечивает достижение следующих  результатов  освоения  изучаемого материала:

  Личностные результаты:

·         представление о математической науке  как сфере  человеческой  деятельности

·          знать и уметь применять широту  процентных вычислений в  жизни

·         креативность мышления, инициатива, находчивость .  активность при решении   прикладных задач

  Метапредметные результаты:

·         умение  самостоятельно планировать пути достижения целей, осознанно выбирать  наиболее эффективные  способы решения  задач

·         умение осуществлять контроль по результату

·         умение видеть математическую  задачу  в контексте проблемной ситуации в других  дисциплинах, в окружающей жизни

·         умение организовывать  учебное сотрудничество и совместную деятельность с учителем и  сверстниками

 

Предметные результаты:

·      понимать содержательный смысл  термина " процент" как специального  способа выражения  доли величины

·         уметь соотносить процент с  соответствующей дробью (50% -- 1/2;  25% --1/4  и т.д.)

·         решать основные задачи на проценты, применять формулу сложных процентов

·         производить прикидку и оценку  результатов  вычислений

·         при вычислении сочетать  устные и письменные  приемы,

·         использовать приемы, рационализирующие вычисления .

 

Для достижения целей курса предлагается следующие способы организации деятельности учащихся на различных уроках:

·         на уроках-лекциях учащиеся учатся конспектировать, анализировать возникновение новых методов решения задач;

·         на уроках-беседах совместными усилиями учителя и учащихся решаются ключевые задачи;

·         на уроках-практикумах учащиеся самостоятельно решают задачи, добиваясь тех или иных навыков, анализируют ошибки и пути их исправления;

 

  Факультативный  курс предусматривает классно-урочную и лекционно-практическую системы обучения. Практическая часть предполагает использование типового школьного оборудования кабинета математики.

   Построение курса позволяет изучать любой из семи модулей, входящих в элективный курс, отдельно, т.е. если ученик пропустил по каким-либо причинам часть курса или в процессе изучения скорректировал уже сделанный выбор, сопоставляя его со своими возможностями.

   К примеру, он может отказаться от изучения VI модуля и увеличить практикум в III, IV модулях, что обеспечит индивидуализацию обучения.  

Разработанный факультативный курс может быть использован учителями математики при подготовке к математическим олимпиадам, подготовки к экзаменам в формате ЕГЭ, централизованному тестированию.

Формы контроля

Зачет по итогам освоения модуля может проводиться в форме:

§  письменной контрольной работы;

§  самостоятельной работы;

§  тестирования;

§  творческой индивидуальной работы

 

Программа факультативного курса предлагает знакомство с теорией и практикой рассматриваемых вопросов и  рассчитана на  34 часа.

Содержание программы факультатива

№ п/п	Разделы,  тема	Количество часов
		Всего	Теория	Практика
1	Модуль 1.  Что надо знать о процентах. Устраняются проблемы в знаниях по решению основных задач на проценты: что такое проценты, как выразить число в процентах, как выразить проценты в десятичной дроби, нахождение процентов от данного числа, нахождение числа по его процентам, процентное отношение двух чисел, изменение величины в процентах, проценты и теория вероятности.	6	1	5
2	Модуль 2.  Решение задач с помощью уравнений и неравенств. Сюжеты задач взяты из действительности: демография, экология, социологические опросы и т. д.	3	1	2
3	Модуль3.  Задачи на процентный прирост и вычисление “сложных  процентов”. Введение базовых понятий экономики: процент прибыли, стоимость товара, бюджетный дефицит и профицит, изменение тарифов и т. д. Решение задач, связанных с банковскими расчётами.	5	1	4
4	Модуль 4. Задачи на смеси, сплавы, концентрацию и процентное содержание. Концентрация вещества, процентное содержание вещества – введение соответствующих понятий и формул.	5	1	4
5	Модуль 5. Проценты на экзаменах. Задачи, предлагаемые в КИМах на ЕГЭ, ГИА.	5	1	4
6	Модуль 6. Олимпиадные задачи. Обобщение полученных знаний при решении задач на проценты. Задачи школьных математических олимпиад. Задачи региональных математических олимпиад.	3	1	2
7	Модуль 7. Что значит жить на проценты. Стратегия ликвидности, стратегия доходности, цепные вклады, государственные краткосрочные облигации.	3	1	2
8	Проценты в мире профессий.	4	0	4

 

 

 

 

 

 

                                                                                          КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

Дата проведения	№ урока	Темы, раздел	Кол-во часов		Элементы содержания	Форма контроля
Что надо знать о процентах?(6 часов)
	1	Вводный тест по теме «Проценты»	1		Понятие процента. Виды задач на проценты: нахождение процента от числа (величины); нахождение числа по его проценту; нахождение процента одного числа от другого	Тестирование.
	2	Что надо знать о процентах?	1			Конспект.
	3	Вычисление процентов  по количеству,  количества по процентам.	1			Конспект, самостоятельная работа.
	4	Сколько процентов составляет одно число от другого? Изменение величины в процентах.	1			Конспект, самостоятельная работа.
	6	Основные задачи на проценты.	2			Контрольная работа.
		Решение задач с помощью уравнений и систем уравнений	3		Сюжеты задач взяты из действительности: демография, экология, социологические опросы и т. д.
	7	Стратегия решения расчётных задач с помощью уравнений.	1			Конспект.
	8	Решение задач с помощью уравнений, систем уравнений.	2			Конспект, самостоятельная работа.
Задачи на процентный прирост и вычисление “сложных  процентов”. (5 часов)
	10	Прикладные задачи	1	Понятия экономики: процент прибыли, стоимость товара, заработная плата, бюджетный дефицит и профицит, изменение тарифов, пеня, вычисление ставок процентов в банках;  процентный прирост; определение начальных вкладов		Конспект.
	11	Формулы сложных процентов в задачах с финансово-экономическим содержанием	1			Конспект.
	12	Распродажа. Тарифы. Штрафы.	1			Конспект.
	13	Банковские операции. Голосование.	1
	14	Задачи на процентный прирост и вычисление “сложных  процентов”.	1			Самостоятельная работа, собеседование.
Задачи на смеси, сплавы, концентрацию и процентное содержание. (5 часов)
	15	Задачи на смеси, сплавы, концентрацию и процентное содержание.	1	Понятия концентрации вещества, процентного раствора; закон сохранения массы. Задачи, связанные  с понятиями концентрации вещества, процентного раствора; на применение  закона сохранения массы. Обобщить полученные знания при решении задач на проценты.		Конспект.
	16	Растворы, смеси. Сплавы.	1			Конспект, самостоятельная работа.
	17	Концентрация и процентное содержание.	1			Конспект, самостоятельная работа.
	18	Комбинированные задачи.	1			Конспект
	19	Задачи на смеси, сплавы, концентрацию и процентное содержание.	1			Самостоятельная работа, собеседование.
Проценты на экзаменах. (5часов)
	20	Простые и сложные проценты.	1	Понятие процента, формулы, виды задач, разные способы их решения		Конспект.
	21	Решение задач из КИМов ЕГЭ и ГИА.	1			Конспект, самостоятельная работа.
	22	Решение экзаменационных задач «на проценты»	1			Конспект, самостоятельная работа.
	23	Решение экзаменационных задач «на проценты»	1			Самостоятельная работа
	24	Решение экзаменационных задач «на проценты»	1			Контрольная  работа.
Олимпиадные задачи. (3 часа)
	25	Примеры олимпиадных задач «на проценты».	1		Понятие процента, формулы, виды задач, разные способы их решения	Конспект.
	26	Олимпиадные задачи «на проценты».	1			Конспект, самостоятельная работа.
	27	Олимпиадные задачи «на проценты».	1			Самостоятельная работа, собеседование.
Что значит жить на проценты? (3часа)
	28	Стратегия ликвидности, стратегия доходности, цепные вклады, государственные краткосрочные облигации.	1		Понятие процента, формулы, виды задач, разные способы их решения	Конспект.
	29	Решение задач.	1			Конспект, самостоятельная работа.
	30	Что значит жить на проценты?	1			Творческая работа.
Проценты в мире профессий. (4 часа)
	31	Прикладные задачи «на проценты»	1		Базовые   понятия экономики: процент прибыли, стоимость товара, заработная плата, бюджетный дефицит и профицит, изменение тарифов, пеня ставка процентов в банках;  процентный прирост;  начальный вклад, формулы простого процентного роста и сложного  процентного роста. Задачи, связанные  с банковскими расчетами: вычисление ставок процентов в банках;  процентный прирост; определение начальных вкладов, задачи на проценты повышенного уровня сложности  с применением формулы простого процентного роста и формулы сложного  процентного роста	Исследовательская                   работа в         малых группах
	32	Прикладные задачи «на проценты»	1			Исследовательская                   работа в         малых группах
	33	Деловая игра «Проценты в мире профессий».	1			Защита исследовательского проекта, игра «Математик-бизнесмен»
	34		1

 

Список литературы для учащихся

 

1.       Усов Н.А. Повторим математику. – Киев, 1994 Дорофеев, Г. В., Седова, Е. А. Процентные вычисления. 10-11 классы: учеб.-метод. пособие. – М.: Дрофа, 2003. – 144 с.

2.      Денищева, Л. О., Бойченко, Е. М., Глазков, Ю. А. и др. Готовимся к единому государственному экзамену. Математика. – М.: Дрофа, 2013. -120 с.

3.      Шевкин, А. В. Текстовые задачи. – М.: Просвещение, 1997. – 112 с.

4.      Корешкова Т.А. Тестовые задания по математике. – М.: Экзамен, 2005

5.       Петрова И.Н. Проценты на все случаи жизни. – Челябинск, 1996

 

Список литературы для учителя

1.      Винокурова Е., Винокуров Н. Экономика в задачах. – М, 1998

2.      Денищева Л.О. Единый государственный экзамен: Математика. – М.: Просвещение, 2008-2013

3.      Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. Задания для проведения письменного экзамена по математике в 9-м классе. – М.: Просвещение, 1994

4.      Корешкова Т.А. Тестовые задания по математике. – М.: Экзамен, 2005

5.      Макарычев Ю.Н. Дополнительные главы к школьному учебнику. – М.: Просвещение, 1996

6.      Математика: 2600 тестов и проверочных заданий для школьников и поступающих в вузы / П.И. Алтынов, Л.И. Звавич, А.И. Медяник и др. – М.: Дрофа, 1999

7.      Петрова И.Н. Проценты на все случаи жизни. – Челябинск, 1996

8.      Рельдман Ф.Г., Рудзитис Г.Е. Химия для 9-х классов средних общеобразовательных учебных заведений. – М.: Просвещение, 1994

9.      Сборник задач по математике для поступающих в вузы / Под редакцией А.Н. Приленко. – М.: Высшая школа, 1989

10.  Симонов А.С. Экономика на уроках математики. – М: Школа-Пресс, 1999

11.  Усов Н.А. Повторим математику. – Киев, 1994

12.  Шарыгин И.Ф. Факультативный курс по математике: Решение задач. – М.: Просвещение, 1994

13.  Вигдорчик, Е., Нежданова, Т. Элементарная математика в экономике и бизнесе. – М., 1997.

14.  И. Н. Петрова. “Проценты на все случаи жизни”. Челябинск. Южно-Уральское книжное издательство. 1996.

15.  Лурье, М. В., Александров, Б. И. Задачи на составление уравнений. – М.: Наука, 1990.

16.  Потапов, М. К., Олехник, С. Н., Нестеренко, Ю. В. Конкурсные задачи по математике: справочное пособие. – М.: Наука, 1992. – 480 с.

17.  В.С.Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа. Москва. “Просвещение”. 1990. стр.22 – Справочный материал по теме “Проценты”.

18.  Журнал “Математика в школе” №10. 2003. стр.2 “Курс по выбору для 9 класса”

19.  Газета “Математика” №30. 2002. стр.29. А.Буслаев “Сложные проценты”.

20.  Газета “Математика” №20. 2004. стр.22; №22. 2004. стр.29; №23. 2004. стр.28. М.Кац. “Проценты”.

 

Приложение1

Вводный тест по теме «Проценты»

 

1. Найдите 25% от 56.

 

1. А) 14         Б) 22,04         В) 20         Г) 25      

 

2. Найдите число, если 1% его равен 75.

 

1. А) 0,75         Б) 7,5         В) 7500         Г) 750     

 

3. Клубника содержит 6% сахара. Сколько килограммов сахара в 27 кг клубники?
1. А) 1,82 кг         Б) 1,62 кг         В) 2,24 кг         Г) 2,42 кг            

 

4. Книга стоила 25 р. После повышения цены она стоит 30,25 р. На сколько процентов возросла стоимость книги?
1. А) на 21%         Б) на 20%         В) на 24%         Г) на 25%            

 

5. Найдите число, 34% которого равны 170.

 

1. А) 57,8         Б) 500         В) 56,5         Г) 510            

 

6. На математической олимпиаде 32% участников получили грамоты. Сколько школьников приняло участие в олимпиаде, если наградили 416 человек?
1. А) 932         Б) 1300         В) 133,1         Г) 1340            

 

7. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
1. А) 330%         Б) 30%         В) 125%         Г) 45%            

 

8. Число уменьшили на 20%. На сколько процентов надо увеличить полученное число, чтобы получить данное число?
1. А) на 20%         Б) на 40%         В) на 25%         Г) на 30%            

 

9. Число 56 составляет 80% от некоторого числа. Найдите среднее арифметическое этих чисел.
1. А) 63         Б) 44,8         В) 126         Г) 56             

 

10.  Сторону квадрата уменьшили на 20%. На сколько процентов уменьшилась его площадь?

А) на 20%         Б) на 36%         В) на 10%         Г) на 40%            

            Таблица ответов:

№ задания	Ответ	№ задания	Ответ
1	А	6	Б
2	В	7	Б
3	Б	8	В
4	А	9	А
5	Б	10	Б

 

Модель занятия

 «Что мы знаем о  процентах?»

Цель: Повторить:

Что такое проценты? Как выразить число в процентах? Как выразить проценты в виде десятичной дроби? Как найти процент от числа? Как найти число по его процентам? Как найти процентное отношение двух чисел?    Проценты на экзаменах по математике.

«Что такое  проценты?  Как выразить число в процентах?»

       Некоторые дроби чаще других встречаются в повседневной жизни, и потому они получили особые названия: половина ( 1/ 2 ), треть (1/3), четверть (1/4) и процент (1/100).

     На практике дробные числа очень часто приходится сравнивать, а делать это удобно тогда, когда они выражены в одинаковых долях – только в третьих, только в четвертых, только в десятых.… Самыми удобными оказались сотые доли, которые и называют процентами (от латинских слов  pro centum – «за сто»). Отсюда и определение: процентом называется дробь 1/100(0,01).

    Обозначают процент знаком %. Интересно его происхождение. Появился он в результате опечатки: наборщик переставил цифры в числе 100. Вот так – 010. Первый ноль чуть – чуть приподняли, второй чуть-чуть опустили, единицу чуть-чуть упростили – вот и получился этот знак. Заменяет он множитель 0,01. 1% = 1/100, или 0,01. Проценты – это числа, представляющие собой частные случаи десятичных дробей. Любое число можно выразить десятичной дробью, значит, и в процентах. Рассудим так: единица содержит сто сотых долей, то есть 100%. Каждое число можно представить в виде произведения единицы на это число, а значит, выразить его в процентах:

     2 = 1 ∙ 2 = 100% ∙ 2 = 200%

     7 = 1 ∙ 7 = 100% ∙ 7 = 700%

     1,534 = 1∙1,534 = 100% ∙1,534 = 153,4%

     0,8 = 1∙ 0,8 = 100% ∙ 0,8 = 80%

Итак, чтобы выразить число в процентах, достаточно умножить его на 100 и поставить знак %. Удобно сначала выразить число в виде десятичной дроби, а затем перенести запятую на два знака вправо и поставить %.

П р и м е р ы: 4 = 4,00 = 400%; 5/10 = 0.5 = 50%; ¾ = 0.75 = 75%.

Как выразить проценты в виде десятичной дроби

Теперь ставится обратная задача: выразить проценты в виде десятичной дроби. Например, 9% означают 9 сотых долей. Записать это можно так: 9% = 9/100 = 0.09. По аналогии выводим:

37% = 37/100 = 0.37;  600% = 600/100 = 6;  290% = 290/100 = 2.9.

Чтобы выразить проценты в виде десятичной дроби, достаточно их число разделить на 100. Это правило можно сформулировать и так: чтобы проценты выразить в виде десятичной дроби, надо в их числе перенести запятую на два знака влево.

П р и м е р ы:  300% = 3;  36.7% = 0.367;  9% = 0.09;  0.1% = 0.001.

Нахождение процентов от данного числа

З а д а ч а. В семенах сои содержится 20% масла. Сколько масла содержится в 700 кг сои?

Р е ш е н и е.

В задаче требуется найти указанную часть (20%) от известной величины (700 кг). Такие задачи можно решать способом приведения к единице. Основное значение величины – 700 кг. Ее мы можем принять за условную единицу. А условная единица и есть 100%.

Кратко условие задачи можно записать так:

700 кг – 100%,

x кг – 20%.

Здесь за  х принята искомая масса масла. Узнаем, какая масса сои приходится на 1 %. Поскольку на 100 % приходится 700 кг, то на 1 % будет приходиться масса, в 100 раз меньшая, то есть 700 : 100 = 7(кг). Значит, на 20 % будет приходиться в 20 раз больше:

        7 ∙   20 = 140(кг). Следовательно, в 700 кг сои содержится 140 кг масла.

Эту задачу можно решить и иначе. Если в условии этой задачи вместо 20 % написать  равное  ему число 0,2, то получим задачу на нахождение дроби от числа. А такие задачи решают умножением. Отсюда получим другой способ решения:

1) 20% = 0,2;  2) 700 ∙ 0,2 = 140 (кг).

Чтобы найти несколько процентов от числа, надо проценты выразить дробью, а затем найти дробь от данного числа.

Нахождение числа по его процентам

З а д а ч а. Из хлопка-сырца получается 24 % волокна. Сколько надо взять хлопка-сырца, чтобы получить 480 кг волокна?

Решение.

480 кг волокна составляют 24 % от некоторой массы хлопка-сырца, которую принимаем за х кг. Будем считать что х кг составляют 100 %. Теперь кратко условие задачи можно записать так:

480кг – 24 %,

х  кг – 100 %.

Решим эту задачу способом приведения к единице. Узнаем, какая масса волокна приходится на 1%. Поскольку на 24 % приходится 480 кг, то, очевидно, на 1% будет приходиться масса в 24 раза меньше, то есть 480 : 24 = 20 (кг). Далее рассуждаем так : если на 1 % приходиться масса в 20 кг, то на 100 % будет приходиться масса, в 100 раз большая, то есть 20 ∙ 100 = 2000 (кг) = 2(т). Следовательно, для получения 480 кг волокна надо взять 2 т хлопка-сырца.

Эту задачу можно решить и иначе.

Если в условии этой задачи вместо 24 % написать равное ему число  0,24, то получим задачу на нахождение числа по известной его части (дроби). А такие задачи решают делением. Отсюда вытекает еще один способ решения:  1) 24% = 0,24;  2)  480:0,24=2000 (кг)=2(т).

Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби решить задачу на нахождение числа по данной его дроби.

Процентное отношение двух чисел

З а д а ч а   1. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?

Решение.

Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить это отношение в процентах:

Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).

Чтобы найти процентное отношение двух чисел, надо найти отношение этих чисел и выразить его в процентах.

З а д а ч а  2. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?

Решение.

Для ответа на вопрос задачи надо найти отношение (частное) числа  45 к 36 и выразить его в процентах:

45 : 36 = 1,25 = 125%

Вопросы и упражнения

Упражнения и задачи

1.                  Найти 1 % от:

а)         34000 р.;                    д) 6 тыс. жителей;

б)          1 км;                          е) 6 га,;

в)         0,3 л;                          ж) 12 р.;

г)         200 г;                         з) 700 овец.

 

2.                   Найти целое, если 1 % от него составляет:

а)         0,2 л;                          в) 10 р.;

б)         30 м³;                         г) 38 чел.

 

3.                   Верно ли, что выплачена вся сумма, если:

а)         в первый раз выплачено 75 % от суммы, а во второй - 15 %;

б)           в первый раз выплачено 37 % от суммы, во второй - 48 %, а в третий - 15 % от остатка.

 

4.                   Найти:

а)         200 % от 200 л;                    г) 0,3 % от 0,3 кг;

б)         25 % от 10 км;                      д) 50 % от 30 чел.;

в)         5 % от 15 л;                          е) 0,1 % от 0,1 %.

 

5.   Что больше:

а)     15 % от 17 или 17 % от 15;

б)     1,2 % от 17 или 12 % от 170;

в)     115 % от 657 или 117 % от 715;

г)     72 % от 150 или 70 % от 152?

 

6.   Сколько будет, если:

а)     100 р. увеличить на 300 %;

б)     500 р. уменьшить на 5 %;

в)     70 % увеличить на 30 %;

г)     40 % уменьшить на 40 %.

 

7.   Найдите:

 

 

8. Найдите:

а)     450 % от 50;              в) 17,2 % от 10;

б)     370 % от 100;            г) 342 % от 10.

 

9.   Вычислите, на сколько процентов:

а)     500 больше 400;                   г) 6000 больше 3000;

б)     400 меньше 500;                  д) 20 кг меньше 60 кг;

в)     3000 меньше 6000;              е) 60 кг больше 20 кг.

 

10.   На сколько процентов изменилась величина, если она:

а)     увеличилась в 2,4 раза; г) уменьшалась в 8 раз;

б)     увеличилась в 3,5 раза; д) уменьшилась в 4 раза;

в)     увеличилась в 10 раз;          е) уменьшилась в 10 раз.

 

11.   Какие из утверждений означают одно и то же:

-     величины относятся как 1:2;

-     величины относятся как 1 : 4?

а)     одна величина вдвое меньше другой;

б)     вторая величина на 300 % больше первой;

в)     первая величина на 300 % меньше второй;

г)     вторая величина на 100 % больше первой;

д)     первая величина на 75 % меньше второй;

е)     одна величина составляет от другой 50 %;

ж)     одна величина в четыре раза меньше другой;

з)         первая величина составляет от второй 25%.

 

12.                  Сколько было, если:

а)         после увеличения на 10 % стало 100 р.;

б)         после уменьшения на 10 % стало 500 р.

 

13.                  Найти, в каком случае первоначальная цена больше:

а)         при скидке 5 % заплачено 100 р.;

б)         при скидке 10 % заплачено 90 р.;

в)         при скидке 20 % заплачено 80 р.

 

14.                  Сколько процентов составляют:

а)         0,5 кг от 6 кг;

б)         375 р. от 100 р.;

в)         250 р. от 200 р.;

г)         15 г от 1 кг;

д)          1048 человек от 3764 человек;

е)         3 мм от 4 м?

 

15.  В открытой степи скорость ветра составляет 8 м/с, а после прохождения через лесную полосу – 4,4 м/с. На сколько процентов уменьшилась скорость ветра после прохождения через лесную полосу?

16.  Посеяли 300 зерен, из них 270 дали всходы. Определите процент всхожести зерен.

17.  В 450 г раствора содержится 27 г соли. Определите процент содержания соли в растворе.

18.  Каким бы чистым ни казался воздух, в нем всегда имеется пыль. Когда мы дышим через нос, пыли задерживается на 60 % больше, чем тогда, когда мы дышим через рот. Во сколько раз при дыхании через нос пыли задерживается больше, чем при дыхании ртом

19.  Лимонный маргарин содержит 64% жира, 16 % сахара и другие продукты. Сколько килограммов жира, сахара и других продуктов содержится в 2,25 т лимонного маргарина?

20. Игра «Математическая эстафета». Найдите число, если

а) 5%;  16%;  20%;  96%;  120%  их равны 480;

б)  10%;  21%;  56%;  84%;  140%  их равны 420;

в)  9%;  30%;  45%;  75%;  225%  их равны 450.

21. Бригада рабочих должна была заасфальтировать участок дороги длиной 840 м. В первый день она выполнила 25%  задания, во второй день 40% , а остальная часть задания была выполнена в третий день. Сколько метров дороги было заасфальтировано в третий день?

22. Из свежих груш получается 18% сушеных.  Сколько взяли свежих груш, если получилось 54 кг сушеных? Сколько получится сушеных груш из 120 кг свежих?

23. Нина прочитала 30%  страниц книги, а если она прочитает еще 50 страниц, то она прочитает 55% страниц книги. Сколько всего страниц в ней?

24. Одна тонна хлопка-сырца дает 350 кг волокна и 500 кг семян. Сколько процентов составляют семена и волокно в отдельности от массы хлопка-сырца? Сколько процентов от массы семян составляет масса волокна?

Или же задачи из сборника для экзаменов части А и В, например,

 Часть А:

1.      Перед Новым годом цены в магазине подарков были снижены на 25%. Некоторый товар до уценки стоил х р. Ученик записал четыре разных выражения для вычисления новой цены товара. Одно из них неверно. Какое?

А)  х – 0,25х         Б) 0,75х             В)  х – 25              Г)  х –

2.      После уценки телевизора его новая цена составила 0,8 старой. Сколько процентов от старой цены составляет новая?

А) 0,8%           Б) 8%                    В) 20%             Г) 80%

Часть В:

3.      (7.8) В прошлом году на два самых популярных факультета университета было подано1100 заявлений. В текущем году число заявлений на первый из этих факультетов уменьшилось на 20%, а на второй увеличилось на 30 %, причем всего было подано 1130 заявлений. Сколько заявлений было подано на каждый из этих факультетов в текущем году? (на 2 балла)  Ответ: 480 и 650

4.      (7.29) Влажность свежескошенной травы 60%, сена 20%. Сколько сена получится из 1 т свежескошенной травы? (на 4 балла). Ответ:500 кг сена.

5.      (7.53) На аукционе одна картина была продана с прибылью 20%, другая с прибылью 50%. Общая прибыль от продажи двух картин составила 30%. У какой картины первоначальная цена была выше и на сколько? (на 6 баллов)  Ответ: первоначальная стоимость первой картины в 2 раза больше, чем второй.

 

Модель занятия

«Решение задач на проценты с помощью уравнений»

Цель урока: Отработка навыков по решению задач на проценты с помощью уравнений

Ход урока:

I Актуализация знания

Тест – опрос. Установите истинность (ложность утверждения)

1) Верно ли:

                      а) 37% = 0,37

                      б) 290% = 2,9

                      в) 9% = 0,9

2) Верно ли:

                      а) 5% от 400 равно 20

                      б) 20% от 300 равно 6

                      в) 1% от 1 м равно 10 см

3) Найти число х:

                       а) 4% его равны 160; х = 400

                       б) 70% его равны 560; х = 800

                       в) 17% его равны 68; х = 400

4) Процентное отношение чисел:

                       а) 150 к 500 равно 30%

                       б) 7 к 10 равно 700%

                       в) 137 к 100 равно 137%

Таблица ответов:

 

1			2			3			4
а	б	в	а	б	в	а	б	в	а	б	в
+	+	–	+	–	+	–	+	+	+	–	+

Условные обозначения:       + «Истинно,         – «Ложно»

II Решение задач

             Задача 1. Одной машинистке на перепечатку рукописи требуется на 12 ч больше, чем другой. Если 25% рукописи перепечатает первая машинистка, а затем к ней присоединится вторая машинистка, то на перепечатку рукописи им понадобиться 35 ч, считая от момента начала работы первой машинистки. За сколько часов могла бы перепечатать рукопись каждая машинистка, работая отдельно?

Решение: Пусть на перепечатку рукописи первой машинистке требуется  ч, тогда второй потребуется  ч. На перепечатку 25% рукописи первая машинистка затратит  ч. Выясним теперь, сколько времени потребуется двум машинисткам на перепечатку оставшихся 75% рукописи. Первая машинистка перепечатывает за один час  часть рукописи, вторая –  часть рукописи, а вместе за час они перепечатывают  часть рукописи. На перепечатку  рукописи им потребуется  ч, т.е.  ч. Отсюда получаем уравнение:

Решив это уравнение, найдем, что оно имеет два корня:  и .

Второй корень не соответствует условию задачи.

Ответ: первой машинистке на перепечатку рукописи требуется 60 ч, а второй – 48 ч.

Задача 2. Положив в банк деньги, вкладчик получил через год прибыль в 240 тысяч рублей. Однако он не стал забирать деньги из банка, а, добавив к ним еще 60 тысяч, снова оставил деньги на год. В результате спустя еще год он получил в банке 1 миллион 100 тысяч рублей. Какая сумма была положена в банк первоначально и какой процент прибыли в год давал банк?

 Решение: Допустим, что первоначальный вклад составляет  тысяч рублей. Тогда процент прибыли за год равен . Сумма вклада, положенного в банк через год, составила  тысяч рублей, т.е.  тысяч рублей. Этот вклад принес доход, равный  тысячам рублей. Всего вкладчик получил 1100 тысяч рублей.Получаем уравнение:

Решив его, найдем, что это уравнение имеет два корня: ,  Выполнив расчеты, можно убедиться, что оба корня соответствует условию задачи.

Ответ: задача имеет два решения: вкладчик вложил первоначально 200 тысяч рублей и получил доход 120% в год или вкладчик вложил первоначально 360 тысяч рублей и получил доход  в год.

Задача 3. Имелось два слитка меди. Процент содержания меди в первом слитке был на 40 меньше, чем процент содержания меди во втором. После того как оба слитка сплавили, получили слиток, содержащий 36% меди. Найдите процентное содержание меди в первом и во втором слитках, если в первом слитке было 6 кг меди, а во втором – 12 кг.

Решение: Обозначим за  массу первого слитка в кг, за  массу второго слитка в кг, получим систему уравнений:

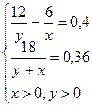
В результате получим: х=30, у=20.    Ответ: 30 кг, 20 кг

Задача 4. Для определения оптимального режима снижения цен социологи предложили фирме с 1 января снижать цену на один и тот же товар в двух магазинах двумя способами. В одном магазине – в начале каждого месяца (начиная с февраля) на 10%, в другом – через каждые два месяца, в начале третьего (начиная с марта) на одно и то же число процентов, причем такое, чтобы через полгода (1 июля) цены снова стали одинаковыми. На сколько процентов надо снижать цену товара через каждые два месяца во втором магазине?

Решение: Пусть  руб. - стоимость товара,  - число процентов. Тогда,

I магазин

       Февраль

        Март    

        ……………………………………

        Июль   

 

II магазин

        Март    

        Май      

        Июль    

По условию задачи через полгода (1 июля) цены снова стали одинаковые, составляем уравнение:

Ответ: на 21%.

Задача5. В магазине одежды проводилась распродажа. Костюмы продавались со скидкой 20%, плащи - со скидкой 40%. Покупатель купил костюм и плащ за 9180 рублей в сумме, заплатив на 32% меньше их суммарной первоначальной цены. Найдите первоначальные цены костюма и плаща

  

               

               

              

              

           

            

              

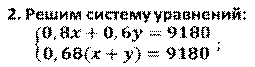
                 Ответ: 5400; 8100

III Задачи для самостоятельной работы

Задача 1. В соответствии с договором фирма с целью компенсации потерь от инфляции была обязана в начале каждого квартала повышать сотруднику зарплату на 3%. Однако в связи с финансовыми затруднениями она смогла повышать ему зарплату только раз в полгода (в начале следующего полугодия). На сколько процентов фирма должна повышать зарплату каждые полгода, чтобы 1 января следующего года зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренной договором.

Решение: Пусть  руб. - зарплата,  - процент повышения зарплаты. Тогда,

По плану

       I квартал         руб.

……………………………

       IV квартал      руб.

Фактически

        I полугодие    руб.

        II полугодие   руб.

       По условию задачи зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренного договором, составляем уравнение:

Ответ: на 6,09 %.

Задача 2. На заводе было введено рационализаторское предложение. В результате время, необходимое для изготовления рабочими некоторой детали, уменьшилось на 20%. На сколько процентов возросла производительность труда этого рабочего?

Решение: Пусть  - производительность труда, а  - весь объем работы. Тогда работа будет выполнена за время . В результате роста производительности труда время на изготовление детали стало равно , соответственно производительность , или . Соответственно рост производительности труда составил:

Ответ: 25%

 

Задача 3. Из жителей города одни говорят только на украинском, другие – только на русском, третьи – на обоих языках. По-украински говорят 85% всех жителей, а по-русски – 75%. Сколько процентов всех жителей этого города говорят на обоих языках?

Решение:

100%-85%=15% - не говорят на украинском;

100%-75%=25% - не говорят на русском;

100%-15%-25%=60% - говорят на обоих языках.

Ответ: 60%

 

Модель занятия

 « Задачи на процентный прирост и вычисление сложных процентов».

      Цель: познакомить с задачами на процентный прирост и с формулой  вычисления сложных процентов.

      Решение задач на процентный прирост и вычисление «сложных процентов» основано на использовании следующих понятий и формул. Пусть некоторая переменная величина А, зависящая от времени t, в начальный момент  t = 0 имеет значение А0, а в некоторый момент времени  t1 имеет значение А1. Абсолютным приростом величины А за время  t1 называется разность А1 – А0, относительным приростом величины А за время t1 – отношение  (А1-А0)/А0  и процентным приростом величины А за время  t1 –величина

((А1-А0)/А0) ∙100%.

      Обозначая процентный прирост величины А через p%, получаем следующую формулу, связывающую значения А0, А1 и процентный прирост p:

((А1-А0)/А0) ∙ 100% = p%

      Запись последней формулы в виде:

А1 = А0 (1+p/100) =  А0+ А0 ´ p/100

      Позволяет по известному значению А0 и заданному значению р вычислить значение А в момент времени t1.

      Пусть теперь известно, что далее при t > t1 величина А имеет процентный прирост р%. Тогда в момент времени t2 = 2´t1 значение величины А2 = А(t2) , будет равно

А2 = А1(1+р/100) = А0(1+р/100)²  .

     В момент времени t3 = 3´t1  значение величины  А3 = А(t2)  есть:

А3 = А2(1+р/100) = А0(1+р/100)³  ;

     В момент времени  n´t1:

Аn = А0(1+р/100)ⁿ.  

     Если за время t1 (на «первом этапе») величина А изменилась на р1%, на «втором этапе» (то есть за время t2 – t1 = t) –  на р2%, на «третьем этапе» (то есть время t3 – t2 = t1) – на p3% и т.д., то значение величины А в момент tn = n ´ t1 вычисляется по формуле:

An = A0 (1 + p1/100) (1 + p2/100)…(1 + pn/100).

П р и м е р 1. Предприятие работало три года. Выработка продукции за второй год работы предприятия возросла на p%, а на следующий год она возросла на 10% больше, чем в предыдущий. Определить, на сколько процентов увеличилась выработка за второй год, если известно, что за два года она увеличилась в общей сложности на 48,59%.

Решение

Обозначим количество продукции, произведенной за первый, второй и третий годы работы предприятия, через А1, А2 и А3 соответственно. По условию задачи за второй год процентный прирост составил p%, а за третий год – (p + 10)%. В соответствии с определением процентного прироста эти условия дают два уравнения:

((А2 – А1)/А1) ∙ 100% = p%, ((A3 – A2)/A2) ∙ 100% = (p + 10)%.

По условию задачи также известно, что за два года производство выросло на 48,59%, то есть в третий год предприятие производило на 48,59% продукции больше, чем в первый год. Это условие можно записать в виде уравнения:

((А3 – А1)/А1) ∙ 100% = 48,59%.

Запишем полученные уравнения в виде следующей системы:

A2 = A1(1 + (p/100)),

A3 = A2(1 + ((p + 10)/100)),

A3 = A1(1 + (48.59/100)).

Умножая первое уравнение на второе, получаем:

A3 = A1(1 + p/100))(1 + ((p + 10)/100)).

Из полученного уравнения и третьего уравнения системы получаем уравнение для отыскания неизвестной величины p:

(1 + (p/100))(1 + ((p + 10)/100)) = 1 + 48.59/100 => p² + 210p – 3859 = 0.

Корни последнего квадратного уравнения: p1 = 17, p2 = 227.

По смыслу задачи подходит первый корень p1 = 17.

О т в е т: 17 %.

2.Сберкасса начисляет ежегодно 3% от суммы вклада. Через сколько лет  внесенная сумма удвоится?

О т в е т: Приблизительно через 33 года.

       3.Население города ежегодно увеличивается на 1/50 наличного числа жителей. Через сколько лет население утроится?

О т в е т: Приблизительно через 55 лет.

4.В букинистическом магазине антикварное собрание сочинений стоимостью 350000 руб. уценивали дважды на одно и то же число процентов. Найти это число, если известно, что после двойного снижения цен собрание сочинений стоит 283 500 рублей.

О т в е т: 10%.

         5.Известно, что вклад, находящийся в банке с начала года, возрастает  к концу года на определенный процент (свой для каждого вклада). В начале года 5/6 некоторого количества денег положили в первый банк. К концу года сумма этих вкладов стала равной 670 ден. Ед., к концу следующего года – 749. Было подсчитано, что если бы первоначально 5/6 исходного количества денег положили во второй банк, а оставшуюся часть – в  первый, то по истечении одного года сумма вкладов в эти банки стала бы равной 710 денежным единицам. В предположении, что исходное количество денег первоначально целиком положено в первый банк, определить величину вклада по истечении двух лет.

Решение  Обозначим через x ден. Ед. первоначальную сумму денег, через a -- процент, на который возрастает сумма за год в первом банке, а через b -- процент, на который возрастает сумма за год во втором банке. К концу первого года сумма вклада в первом банке стала равной:

5/6∙x ∙(1 + a/100);

во втором банке:

 1/6∙x ∙(1 + b/100),

а к концу второго года соответственно:

5/6∙x ∙(1 + a/100)²  и 1/6∙x∙ (1 + b/100)²

Из условия задачи имеем, что сумма вкладов к концу первого года составляет 670 ден. Ед., а к концу второго года – 749, поэтому имеем:

5/6∙x ∙(1 + a/100) + 1/6∙x ∙(1 + b/100) = 670,                (1)

5/6∙x ∙(1 + a/100)²   + 1/6∙x ∙(1 + b/100)²   = 749,              (2)

Если во второй банк положить 5/6x ден. Ед., а в первый банк 1/6x, то сумма вкладов к концу года составила бы:

5/6∙x∙ (1 + b/100) + 1/6∙x ∙(1 + a/100),

что равнялось бы 710 ден. ед. Поэтому:

                                              5/6∙x ∙(1 + b/100) + 1/6∙x∙ (1 + a/100) = 710.        (3)

Для нахождения ответа в задаче надо из системы трех уравнений (1), (2) и (3) найти две неизвестные x и a.

Для этого поступим следующим образом. Уравнения (1) и (3) перепишем так:

5(1 + a/100) + (1 + b/100) = (6 ´ 670)/x,

(1 + a/100) + 5(1 + b/100) = (6 ´ 710)/x.

Из получившейся системы уравнений найдем, что

1 + a/100 = 660/x, 1 + b/100 = 720/x.

Подставляя 660/x вместо 1 + a/100 и 720/x вместо 1 + b/100 в уравнение (2), приходим к уравнению:

5/6∙x ∙(660/x)² + 1/6∙x ∙(720/x)² = 749,

имеющему единственный корень x = 660, и тогда 1 + α/100 = 660/600 = 1,1. Если исходное количество денег положить на два года в первый банк, то к концу второго года величина вклада составит:

x∙(1 + a/100)² = 600 ∙ 1.1² = 726 ден. ед.                      О т в е т:  726 ден. ед.

 

Модель занятия

 «Задачи на концентрацию и процентное содержание».

Цель: «познакомить с формулами, на которых основано решение задач на концентрацию и процентное содержание».

  Решение задач на концентрацию и процентное содержание основано на использовании следующих понятий и формул.

Пусть даны три следующих вещества А, В и С с массами Ма, Мb и Мс. Масса смеси, составленной из этих веществ, равна Ma + Mb + Mc.

Массовой концентрацией вещества А в смеси называется величина ca, вычисляемая по формуле:

Соответственно массовые концентрации веществ В и С в этой смеси вычисляются по формулам:

Массовые концентрации ca, cb и cc связаны равенством

ca + cb + cc = 1.

Процентными содержаниями вещества А, В, С в данной смеси называются величины pa%, pb% и pc% соответственно, вычисляемые по формулам:

pa % = ca ∙ 100 %, pb % = cb ∙ 100 %, pc % = cc ∙ 100 %.

По аналогичным формулам вычисляются концентрации веществ в смеси и для случая, когда число различных смешиваемых веществ (компонент) равно двум, четырем, пяти и т.д.

Объемные концентрации веществ в смеси определяются такими же формулами, как и массовые концентрации, только вместо масс компонент Ma, Mb и Mc в этих формулах будут стоять объемы компонент Va, Vb и Vc. В тех случаях, когда речь идет об объемных концентрациях, обычно предполагается, что при смешивании веществ объем смеси будет равен сумме объемов компонент. Это предположение не является физическим законом, а представляет собой соглашение, принимаемое при решении задач на объемную концентрацию.

П р и м е р 1. В сосуд емкостью 6л налито 4л  70%-ного раствора серной кислоты. Во второй сосуд той же емкости налито 3л  90%-ного раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нем получился r%-ный раствор серной кислоты? Найти все значения r, при которых задача имеет решение.

Решение  Обозначим через xл объем 90%-ного раствора серной кислоты, который переливается из второго сосуда в первый. В этом объеме содержится 9x/10л чистой (100%-ной) серной кислоты. Первоначально в первом сосуде объем чистой серной кислоты был равен (7/10) ∙ 4 л. После того как в первый сосуд долили xл 90%-ного раствора серной кислоты, в нем будет содержаться (7/10) ∙4 + (9/10) ∙ x л чистой серной кислоты. Используя определение объемного процентного содержания, в соответствии с условием задачи получаем уравнение:

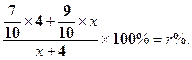
Решая это уравнение, находим величину перелитого объема:

Остается выяснить, при каких значениях r задача имеет решение. Из условия задачи, очевидно, что количество доливаемого раствора не может превысить 2л, так как объем первого сосуда равен 6л, то есть  0 <x<2. Используя найденное значение для x, получим ограничения на r:

Решая данное неравенство (с учетом того, что 70 £ r £ 90), получим 70 £ r £ 76 ⅔.

О т в е т:          л,

Задача имеет решение при 70 £ r £ 76 ⅔.

 

П р и м е р 2.  Имеется два раствора серной кислоты в воде: первый-- 40%-ный, второй-- 60%-ный. Эти два раствора смешали, после чего добавили 5 кг чистой воды и получили 20%- ный раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-ного раствора, то получился бы 70%-ный раствор. Сколько было 40%-ного и 60%-ного растворов?

Решение.  Обозначим через x кг количество 40%-ного и через y кг – количество 60%-ного растворов. Если сольем х кг 40%-ного раствора, у кг 60%-ного раствора и 5 кг чистой воды, то получим раствор весом в (х + у + 5) кг, который по условию содержит 20% кислоты.  Поскольку в х кг 40%-ного раствора находится 0,4 кг кислоты, а в у кг 60%-ного раствора находится 0,6 кг кислоты, то в (х + у + 5) кг находится (0,4х + 0,6у) кг кислоты, что составляет 20% от (х + у + 5) кг, то есть, имеем уравнение:

0,4х + 0,6у = 0,2(х + у + 5).

Если вместо 5 кг воды добавить 5 кг 80%-ного раствора, то получим раствор весом        (х + у + 5) кг, в котором будет (0,4х + 0,6у + 4) кг кислоты, что составляет 70% от (х + у + 5) кг, то есть, имеем уравнение:

0,4х + 0,6у + 4 = 0,7(х + у + 5).

Итак, для нахождения х и у получили систему уравнений:

которую можно записать в виде:

Решением этой системы является пара чисел х =1 и у = 2. Следовательно,  было 1 кг 40%-ного и 2 кг 60%-ного растворов серной кислоты.

О т в е т:  1 кг 40%-ного и 2 кг 60%-ного растворов.

Решение задач

1.  Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?

О т в е т:  1,5 кг.

     2.  Имеются два слитка сплавов меди и олова. Первый весит 3 кг и содержит 40% меди, второй весит 7 кг и содержит 30% меди. Какого веса нужно взять куски этих слитков, чтобы после их совместной переплавки получить 8 кг сплава, содержащего r% меди? найти все значения r, при которых задача имеет решение.

3.  В двух сосудах находился раствор вещества различной концентрации, причем в первом сосуде на m литров меньше, чем во втором. Из каждого сосуда взяли одновременно по n литров и взятое из первого сосуда перелили во второй, а взятое из второго – в первый. После этого концентрации растворов в обоих сосудах стали одинаковыми. Найти, сколько литров раствора было в каждом сосуде.

4.  Даны три различных соединения железа. В каждом кубическом сантиметре (см³) первого соединения содержится на 3/20г железа меньше, чем в каждом см³ второго соединения, а в каждом см³ третьего соединения – в 10/9 раза больше, чем в каждом см³ первого соединения. Кусок третьего соединения, содержащий 1г железа, имеет объем на 4/3 см больший, чем кусок второго соединения, также содержащий 1г железа. В каком объеме третьего соединения содержится 1г железа?

У к а з а н и е: воспользоваться формулой m = pV, связывающей массу, плотность и объем вещества.

О т в е т:  в объеме 4 см³.

5.  Имеются два сплава, состоящих из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй – 26% меди. Процентное содержание цинка в первом

и втором сплавах одинаково. Сплавив 150г первого сплава и 250г второго, получим новый сплав, в котором будет 30% цинка. Определить, сколько килограммов  олова содержится в  новом сплаве.

Решение.

Обозначим через х кг количество олова, содержащегося в получившемся новом сплаве, а через у кг – количество цинка, содержащегося в первом сплаве. Так как получившийся новый сплав весит 400 кг и в нем 30% цинка, то он содержит цинка

(400/100)  30 = 120кг, а тогда во втором сплаве цинка (120 – у) кг. По условию задачи процентное содержание цинка в первом и втором сплавах одинаково, поэтому имеем:

(y/150)∙100=((120-y)/250)∙100

Из этого уравнения находим, что у = 45. Поскольку  первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет (40/100) ∙ 150 = 60 кг, а во втором сплаве олова будет (х – 60) кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет (250/100) ∙26 = 65 кг. Во втором сплаве олова содержится (х – 60) кг, цинка 120 – 45 = 75 кг, меди 65 кг и, так как все это весит 250 кг, то имеем х – 60 + 75 + 65 = 250, откуда х = 170.

О т в е т:  170 кг.

6.  Имеются три сплава. Первый сплав содержит 30% никеля и 70% меди, второй – 10% меди и 90% марганца, третий – 15% никеля, 25% меди и 60% марганца. Из них необходимо приготовить новый сплав, содержащий 40% марганца. Какое наименьшее и какое наибольшее процентное содержание меди может быть в этом новом сплаве?

О т в е т:  40 %;  43⅓ %.                                                 

Модель занятия

Проценты на экзаменах».

ЗАДАЧИ ЦЕНТРАЛИЗОВАННОГО ТЕСТИРОВАНИЯ ДЛЯ 9 КЛАССА

1.      В первой смене летнего лагеря отдыхали 550 школьников. Во второй смене число мальчиков сократилось на 4%, а число девочек увеличилось на 4%. Всего же во второй смене отдыхало 552 школьника. Сколько мальчиков отдыхало в первой смене?

Ответ: 250 мальчиков.

2.      Колхоз обычно засевал пшеницей и ячменем 125 Га угодий. После увеличения площади посевов пшеницы на 10% и уменьшения площади посева ячменя на 8 % занимаемая ими площадь стала равной 124 Га. Какова была первоначальная площадь пшеничного поля?

Ответ: 50 Га.

3.      На складе хранилось 500 куб. метров досок и бруса. После продажи 10% досок и 15% бруса осталось 445 куб, метро пиломатериалов. Сколько кубических метров досок продали?

Ответ: 40 куб. метров.

4.      Две фракции областной думы объединяли 60 депутатов. При раздельном голосовании по законопроекту проголосовали «против» 15 % членов первой фракции и 10% - второй, а поддержали законопроект 52 депутата этих фракций. Сколько депутатов входит в первую фракцию?

Ответ: 40 депутатов.

5.      В двух школах поселка училось 640 мальчиков. Через год число мальчиков в первой школе увеличилось на 5 %, а во второй - уменьшилась на 10%, а общее количество мальчиков стало равным 612. Сколько мальчиков училось в первой школе первоначально?

Ответ: 240 мальчиков.

6.      На двух поддонах лежало 15 000 штук красного и белого кирпича. На строительство перегородки было израсходовано 85% красного и 90%  белого кирпича, после чего осталось 1830 кирпичей. Сколько красных кирпичей было первоначально?

Ответ: 6600 штук.

7.      В контейнере хранилось в общей сложности 500 кг гвоздей и шурупов. Порсле продажи 10% гвоздей и 5% шурупов их масса уменьшилось на 460 кг.Сколько килограммов гвоздей продали?

Ответ: 30 кг.                                                                           

ЗАДАЧИ ЕГЭ .
        1. Агрофирма предполагает продать моркови на 10% меньше ,чем в прошлом году. На сколько процентов агрофирма должна повысить цену на свою морковь, чтобы

получить за неё на 3,5% больше денег, чем в прошлом году.

Решение.
Пусть q₀-объём продаж прошлого года ;

           p₀- цена продаж прошлого года;

           p₀q₀- выручка прошлого года;

           q₁- объём продаж текущего года;

           p_1- цена продаж текущего года;

           p₁q₁- выручка текущего года.
По условию задачи p₁q₁= 1,035 p₀q_0,

причём q_{1 =} 0,9 q₀

                     p₁₌(1+x)p₀;

где x-доля повышения цены на морковь.
Значит , (1+x)p_0*0,9 q₀₌1,035 p₀q_0,

              0,9(1+х)=1,035

              0,9х=1,035-0,9

              х=

              х=0,15

Значит ,агрофирма должна повысить цену на морковь на 15%, чтобы получить прибыль на 3,5% больше ,чем в прошлом году.

2.  В бидон налили 3 литра молока однопроцентной жирности и 7 литров молока 6% жирности. Какова жирность полученного молока (в процентах)?

Решение.
При решении этой задачи можно воспользоваться формулой

n_{конц =}

n_{конц = =  =  =} 0,045

            0,045*100% = 4,5%

Значит, жирность полученного молока-4,5%

3. При покупке ребёнку новых лыж с ботинками родителям пришлось заплатить на 35% больше ,чем два года назад, причём лыжи подорожали с тех пор на 20% ,а ботинки – на 70%. Сколько процентов от стоимости лыж с ботинками составляла два года назад стоимость лыж?

Решение.
1,2х+1,7у = 1,35(х+у),

Где х р.- стоили лыжи два года назад;

       у р.- стоили ботинки два года назад.

у = х;    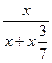         =  =     Ответ: 70%

Решение задач

1.      Семья со­сто­ит из мужа, жены и их до­че­ри сту­дент­ки. Если бы зар­пла­та мужа уве­ли­чи­лась вдвое, общий доход семьи вырос бы на 67%. Если бы сти­пен­дия до­че­ри умень­ши­лась втрое, общий доход семьи со­кра­тил­ся бы на 4%. Сколь­ко про­цен­тов от об­ще­го до­хо­да семьи со­став­ля­ет зар­пла­та жены?

 

2.      Цена хо­ло­диль­ни­ка в ма­га­зи­не еже­год­но умень­ша­ет­ся на одно и то же число про­цен­тов от преды­ду­щей цены. Опре­де­ли­те, на сколь­ко про­цен­тов каж­дый год умень­ша­лась цена хо­ло­диль­ни­ка, если, вы­став­лен­ный на про­да­жу за 20 000 руб­лей, через два года был про­дан за 15 842 руб­лей.

 

3.      Митя, Антон, Гоша и Борис учре­ди­ли ком­па­нию с устав­ным ка­пи­та­лом 200 000 руб­лей. Митя внес 14% устав­но­го ка­пи­та­ла, Антон – 42 000 руб­лей, Гоша – 12% устав­но­го ка­пи­та­ла, а остав­шу­ю­ся часть ка­пи­та­ла внес Борис. Учре­ди­те­ли до­го­во­ри­лись де­лить еже­год­ную при­быль про­пор­ци­о­наль­но вне­сен­но­му в устав­ной ка­пи­тал вкла­ду. Какая сумма от при­бы­ли 1 000 000 руб­лей при­чи­та­ет­ся Бо­ри­су? Ответ дайте в руб­лях.Ре­ше­ние.

Пусть цена хо­ло­диль­ни­ка еже­год­но сни­жа­лась на про­цен­тов в год. Тогда за два года она сни­зи­лась на , от­ку­да имеем:

 

Ответ: 11.

Ответ: 11

 

4.      В сосуд, со­дер­жа­щий 5 лит­ров 12–про­цент­но­го вод­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства, до­ба­ви­ли 7 лит­ров воды. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

 

5.      Сме­ша­ли не­ко­то­рое ко­ли­че­ство 15–про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 19–про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

6.      Сме­ша­ли 4 литра 15–про­цент­но­го вод­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с 6 лит­ра­ми 25–про­цент­но­го вод­но­го рас­тво­ра этого же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?Ре­ше­ние.

Кон­цен­тра­ция рас­тво­ра равна . Пусть объем по­лу­чив­ше­го­ся рас­тво­ра лит­ров. Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го рас­тво­ра равна:

 

Ответ: 17.

Ответ: 17

 

7.      Пер­вый сплав со­дер­жит 10% меди, вто­рой – 40% меди. Масса вто­ро­го спла­ва боль­ше массы пер­во­го на 3 кг. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав, со­дер­жа­щий 30% меди. Най­ди­те массу тре­тье­го спла­ва. Ответ дайте в ки­ло­грам­мах.

8.      Ви­но­град со­дер­жит 90% влаги, а изюм — 5%. Сколь­ко ки­ло­грам­мов ви­но­гра­да тре­бу­ет­ся для по­лу­че­ния 20 ки­ло­грам­мов изюма?

 

9.      Име­ет­ся два спла­ва. Пер­вый сплав со­дер­жит 10% ни­ке­ля, вто­рой – 30% ни­ке­ля. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав мас­сой 200 кг, со­дер­жа­щий 25% ни­ке­ля. На сколь­ко ки­ло­грам­мов масса пер­во­го спла­ва мень­ше массы вто­ро­го?

10.  Име­ют­ся два со­су­да. Пер­вый со­дер­жит 30 кг, а вто­рой – 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если эти рас­тво­ры сме­шать, то по­лу­чит­ся рас­твор, со­дер­жа­щий 68% кис­ло­ты. Если же сме­шать рав­ные массы этих рас­тво­ров, то по­лу­чит­ся рас­твор, со­дер­жа­щий 70% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом со­су­де?

11.  Кли­ент А. сде­лал вклад в банке в раз­ме­ре 7700 руб­лей. Про­цен­ты по вкла­ду на­чис­ля­ют­ся раз в год и при­бав­ля­ют­ся к те­ку­щей сумме вкла­да. Ровно через год на тех же усло­ви­ях такой же вклад в том же банке сде­лал кли­ент Б. Еще ровно через год кли­ен­ты А. и Б. за­кры­ли вкла­ды и за­бра­ли все на­ко­пив­ши­е­ся день­ги. При этом кли­ент А. по­лу­чил на 847 руб­лей боль­ше кли­ен­та Б. Какой про­цент го­до­вых на­чис­лял банк по этим вкла­дам

12.  Кли­ент А. сде­лал вклад в банке в раз­ме­ре 6200 руб­лей. Про­цен­ты по вкла­ду на­чис­ля­ют­ся раз в год и при­бав­ля­ют­ся к те­ку­щей сумме вкла­да. Ровно через год на тех же усло­ви­ях такой же вклад в том же банке сде­лал Б. Ещё ровно через год кли­ен­ты А. и Б. за­кры­ли вкла­ды и за­бра­ли все на­ко­пив­ши­е­ся день­ги. При этом кли­ент А. по­лу­чил на 682 рубля боль­ше кли­ен­та Б. Какой про­цент го­до­вых на­чис­лял банк по этим вкла­дам?

13.  В 2008 году в го­род­ском квар­та­ле про­жи­ва­ло че­ло­век. В 2009 году, в ре­зуль­та­те стро­и­тель­ства новых домов, число жи­те­лей вы­рос­ло на , а в 2010 году на по срав­не­нию с 2009 годом. Сколь­ко че­ло­век стало про­жи­вать в квар­та­ле в 2010 году?

 

Модуль занятия  «Олимпиадные задачи»
            1.В школе все учащиеся сидят за партами по двое, причем у 60% мальчиков сосед по парте - тоже мальчик, а у 20% девочек сосед по парте - тоже девочка. Сколько процентов учащихся этой школы составляют девочки? 

Пусть всего в школе  мальчиков и  девочек. Заметим, что число мальчиков, сидящих с девочками, равно числу девочек, сидящих с мальчиками, т.е. число 0,4 (100% - 60% = 40% от числа ) равно 0,8 (100% - 20% = 80% от ). Поэтому  = 2, и девочки составляют  учащихся.

Ответ: 33 %.

2. Бригада лесорубов решила вырубить сосновый лес, но экологи запротестовали. Тогда бригадир успокоил экологов, сказав им: «В нашем лесу сосны составляют 99% от всего леса. После рубки леса сосны будут составлять 98% всех деревьев». Какую часть леса вырубит бригада?

Решение: При рубке сосен количество деревьев других пород не изменится. Вначале эти деревья составляли 1% леса, а после рубки составят 2% леса. Но если доля прочих деревьев возрастет в 2 раза, то это значит, что лес уменьшится в 2 раза.

Ответ: вырубили половину леса.

3. М.В.Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки хотя бы на квас, если цены еще вырастут на 20%?

Решение: Пусть х и к – первоначальная цена хлеба и кваса. Тогда х + к = 1,2(0,5х + к). Отсюда следует, что х = 0,5к. Т.к. вначале денежки хватало на х + к, то ее хватало на 1,5х. После второго повышения цен квас будет стоить 1,44к. Поэтому денежки на квас хватит.

Ответ: хватит.

4. Цены снизили на 20%. На сколько процентов больше можно купить товаров на те же деньги?
Ответ: на 25%.

5. В школе все учащиеся сидят за партами по двое, причем у 60% мальчиков сосед по парте - тоже мальчик, а у 20% девочек сосед по парте - тоже девочка. Сколько процентов учащихся этой школы составляют девочки? 

Решение: Пусть всего в школе  мальчиков и  девочек. Заметим, что число мальчиков, сидящих с девочками, равно числу девочек, сидящих с мальчиками, т.е. число 0,4 (100% - 60% = 40% от числа ) равно 0,8 (100% - 20% = 80% от ). Поэтому  = 2, и девочки составляют  учащихся.


6. На острове рыцарей и лжецов (лжецы всегда лгут, рыцари всегда говорят правду) каждый болеет ровно за одну футбольную команду. В опросе приняли участие все жители острова. На вопрос «Болеете ли Вы за «Спартак»?» ответили «Да» 40% жителей. На аналогичный вопрос про «Зенит» утвердительно ответили 30%, про «Локомотив» - 50%, а про ЦСКА – 0%. Какой процент жителей острова действительно болеет за «Спартак»?

Решение: Пусть x% жителей острова составляют лжецы. Тогда (100 – х)% составляют рыцари. Так как каждый рыцарь утвердительно ответил ровно на один из вопросов, а каждый лжец – на три, то (100 – х) + 3х = 40 + 30 + 50, откуда х = 10. Так как ни один из жителей острова не сказал, что болеет за ЦСКА, то все лжецы болеют за ЦСКА. Каждый из них заявил, что болеет за «Спартак», поэтому действительно болеют за «Спартак» 40% - 10% = 30% жителей.

Задачи на «сложные проценты»
1. В 2009 году в городском квартале проживало 3000 человек. В 2010 году, в результате строительства новых домов, число жителей выросло на 15%, а в 2011 году – на 20% по сравнению с 2010 годом. Сколько человек стало проживать в квартале в 2011 году?
Ответ: 4140.

2. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 9% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Ответ: на 30%.

3. За несколько дней до соревнований спортсмен стал «сбрасывать» вес, уменьшая каждые сутки вес своего тела на одно и то же число процентов от предыдущего значения. Определите, на сколько процентов в сутки спортсмен уменьшал свой вес, если известно, что за последние двое суток до соревнований его вес уменьшился с 62,5кг до 57,6кг.
Ответ: на 4%.

Распродажа, «скидка», цена товара.

1. Заработок рабочего повысился на 20 %, а цены на продукты и другие товары снизились на 15 %. На сколько процентов рабочий теперь на свой заработок может купить больше товаров, чем прежде?

Решение: Примем прежний заработок рабочего за 10 р. И пусть он покупает только один продукт по 1р. за килограмм, т. е. 10 кг. После повышения на 20 % заработок рабочего стал 12 р, а цена продукта после снижения цены на 15 % - 0,85р. за 1кг. Теперь рабочий может купить 12: 0,85 =14,1 (кг ), т. е. 4,1 : 10 = 0,41, т. е. на 41 5 больше, чем прежде. Ответ: на 41 % больше.

2. Цена товара была повышена на 12%. На сколько процентов надо снизить новую цену, чтобы подучить первоначальную?
Решение: a –первоначальная цена, p –процентные снижения. a + 0.12a = 1,12a –цена после повышения.
1,12a – 1,12a · 0,01p –после снижения. По условию 1,12 a -1,12a · 0,01p= a. p = 10.
Ответ: 10.

3. Стоимость сырья для производства йогуртов возросла на 30 %, а заработная плата – на 5 %. Как изменится себестоимость производства 1 единицы продукции, если доля расходов на заработную плату в общих производственных расходах составляет 20 %, а на сырье- 80 %?
Решение: примем себестоимость производства 1 йогурта за единицу. Расходы на сырье 0,8, на заработную плату 0,2. После повышения цен затраты на сырье составляют 0.8 · 1,3 = 1,04, а на заработную плату 0,2 · 1,05 = 0,21. Общее изменение себестоимости 1,04 + 0,21 = 1,25, т. е. себестоимость производства увеличилась на 25 %

Модель занятия   «Что, значит, жить на проценты?».

 

Цель: объяснить, что  значит, жить на проценты, что такое доходность. Создать инициативные группы для проведения исследований по проблеме «Лучший вклад на сегодня».

Сегодня многие учреждения предлагают потребителям сберегательные услуги, которые выглядят как заманчивая альтернатива «чулку». Если у вас есть сбережения, то непременно приходится решать вопрос – куда вложить деньги, как их сохранить, или преумножить.

Можно выбрать:

-- стратегию ликвидности – деньги вкладываются так, чтобы можно было получить их обратно в случае необходимости;

-- стратегию доходности – деньги вкладываются с целью спасения их от инфляции и получения дохода от них.

С точки зрения «процентов» для нас представляет интерес стратегия доходности.

 

Доходность.

Надо с настороженностью и пониманием относиться к многочисленным рекламным объявлениям, обещающим большие проценты на вклад, которые, к сожалению, не всегда корректны.  А все дело в том, что процент можно считать по-разному.

Принято различать простые и сложные проценты. Предположим,  вы положили в банк 100 000 руб. с условием, что на ваш вклад будут начисляться ежемесячно 10%, которые вы сможете получать все сразу в конце года. Если банк начисляет каждый месяц по 10000 руб., то речь идет о простых процентах. Если за первый месяц начислено 10 000 рублей, за второй 11 000 руб. (10% от 110 000 рублей – суммы первоначального вклада и процентов за предыдущие месяцы), за третий – 12 100 руб. и т.д. – то речь идет о сложных процентах.

Формула расчета сложных процентов выглядит так:

(1+X)¹²-1=Y                                       (1)

и

                                    (2)

где Х – величина месячных процентов ( в десятичной форме, то есть величина процентов, поделенная на 100), У – величина годовых процентов ( в десятичной форме).

 

З а д а ч а 1. Банк обещает выплатить 10% на сумму вклада ежемесячно. Сколько процентов за год реально сможет получить вкладчик?

Решение

Сумма вклада будет составлять после:

1 месяца (1000 + 1000 ∙ 0,1) руб. = 1000 ∙ 1,1 руб. = 1100 руб.

2месяцев (1100 + 1100 ∙ 0,1) руб. = 1000 ∙ (1,1)² = 1210 руб.

……………………………………………………………………..

12 месяцев 1000 ∙ (1,1)¹² = 3138,4 руб.

Вклад ежемесячно увеличивается в 1,1 раза. Следовательно, за 12 месяцев он увеличится в (1,1)¹² = 3,1384 раза, что составляет прирост на 214% или по формуле (2):

(1 + 0,1)¹² - 1 = 2,14,

где X = 0.1 и Y = 2.14.

О т в е т:  214%.

З а д а ч а 2.  Банк начисляет проценты раз в квартал в размере 30% на вклад.  Сколько процентов годовых получит вкладчик, если он не забирает деньги в течение одного года?

Решение.

Так как вклад ежеквартально увеличивается в 1,3 раза, то за четыре квартала он увеличится в 1,3 раза, то за четыре квартала он увеличится в (1,3)⁴ =2,8561 раза, что составляет прирост на 186%, или, используя формулу (2) для сложных процентов:

(1+0,3)⁴ - 1=1,86.

О т в е т: 186%.

З а  д а ч а  3. Банк обещает 120% в год с выплатой в конце года. Сколько  процентов  ежемесячно начисляет банк?

Решение. Так как в данном случае Y= 120%=1,2, то получим

а не 10% (120/12) , как следовало бы ожидать в случае простых процентов.

О т  в е т: 6,8%.

З а д а ч а 4. Что выгодней:  20% годовых в валюте или 140% годовых в рублях?

Решение.Предположим, что мы делаем одновременно два вклада сроком на один год. Для простоты положим, что вкладываем 1 долл.  и 5000 руб. Через год по первому  вкладу получим 1,2 долл. (вклад + проценты по нему), по второму – 12000 руб. Эти вклады  будут равноценными, если курс рубля по отношению к доллару составит 10000 руб. за доллар (12000 / 1,2). Это означает, что доллар должен вырасти за год в 2 раза, то есть на 100%, то есть курс доллара по отношению к рублю растет приблизительно на 5,76 % в месяц

или исходя из курса 5000 руб/долл на 288 руб. за один доллар в месяц.

Следуя данной методике расчета, очевидно, что в 1995 году рублевый вклад был однозначно выгодней, т. к. за счет введения валютного коридора курс доллара по отношению к рублю изменился за год  приблизительно на 30 %.  А как обстоит дело сейчас,  вы ответите сами на этот вопрос.

Пользуясь этой методикой и собственной оценкой тенденции соотношения рубля и доллара, вы  сможет оценить преимущество вклада в рублях или в валюте.

1 этап проекта: « Лучший вклад на сегодня».

 Формирование инициативной группы для проведения исследования по проблеме.

2 этап проекта: «Лучший вклад на сегодня». Самостоятельная работа.

 Посетите ближайшую сберкассу. Выпишите всевозможные вклады, предлагаемые банком. Постарайтесь выяснить какой вклад выгоднее, для вклада, например, 300000 рублей  (сумму вклада для разных вариантов можно изменить).

                                   Модель занятия  «Цепные вклады».

Цель: познакомить  с понятием цепных вкладов.

Так как в наше время на длительный срок (порядка года и более), ввиду непредсказуемости ситуации в стране, вклады в финансовые учреждения делать неблагоразумно, то  повсеместно практикуется размещение средств на краткосрочном вкладе ( до полугода) с неоднократным переоформлением вклада по истечением сроков. Например, вместо вклада на год делается вклад на три месяца. Затем вклад и проценты по нему вносятся вновь на трехмесячный вклад и т. д. Такой вклад принято называть цепным.

Как правило, банки устанавливают стандартные ставки, то есть ставки, по которым годичный вклад по стандартным условиям (проценты начисляются раз в год и присоединяются к вкладу) приносит такой же доход, как и цепной вклад.

Но иногда банки так устанавливают ставки, что по цепному вкладу за год  доход получается больше, чем по годовому. Задачей вкладчика и является выбрать вариант, по которому выгоднее вложить средства.

 

З а д а ч а 5. Что выгоднее – трехмесячный вклад под 90% годовых, шестимесячный под 105 % или годовой под 120%?

Решение

При такой постановке задачи мы должны сравнить наш доход за год.

а) четыре трехмесячных вклада:

- коэффициент увеличения вклада за три месяца  

- коэффициент увеличения вклада за год равен коэффициенту увеличения вклада за срок вклада, возведенному в степень, равную кратности цепного вклада ( в нашем случае она равна 4 (см. задачу 2 данного раздела)):

- то есть, за год мы получим:

(2,25 – 1) ∙  100% = 125% годовых;

б)  два шестимесячных вклада:

- коэффициент увеличения вклада за шесть месяцев:

- то есть за год мы получим:

[(1.525)² - 1] ∙ 100% = 133% годовых.

Таким образом, по банковским ставкам, приведенным в данной задаче, наиболее выгодным оказывается цепной вклад на шесть месяцев (133% годовых), затем вклад четыре по три месяца (125% годовых) и, наконец, наименее выгодный – годовой вклад по 120%.

Аналогичным образом можно рассчитать стандартные ставки цепных вкладов при любых конкретных ставках банков, то есть необходимо рассчитать все возможные варианты цепных вкладов и сравнить стандартные ставки для всех вариантов цепных вкладов, и если существующие ставки позволяют по цепным вкладам получить больший доход, то выгоднее вместо длительных вкладов делать краткосрочные с последующим их переоформлением.

3 этап проекта: «Лучший вклад на сегодня»

Обсуждение полученных результатов исследований групп с учителем.  Подготовка к защите проекта.)

 

Государственные краткосрочные облигации (ГКО).

Во всем мире одним из наиболее надежных способов вложения денег является приобретение ценных государственных бумаг. В настоящее время у нас в стране появились бумаги, которые выглядят наиболее привлекательными и заслуживающими внимание. Это – государственные краткосрочные облигации (ГКО). Что же такое ГКО?

Государство продает эти ценные бумаги дешевле номинала (со скидкой – дисконтом), а через определенное время погашает – но уже по номиналу. Разница между номиналом облигации и ценой покупки и является доходом вкладчика.

Доходность определяется как отношение получаемого дохода к вложенным средствам, с учетом того срока, на который был сделан вклад.

Если вы затратили А ден. ед., а получили В ден. ед. за Т дней, то доходность в процентах годовых по ставке  простого процента рассчитывается так:

Так, например, приобретя трехмесячную облигацию номиналом 100 000 руб. за       70 000  руб., получим доходность по ставке простого процента:

Так, в 1995 год доходность по ГКО превышала банковские ставки по депозитам. Но справедливости ради, надо сказать, что по состоянию на конец 1995 года частные вкладчики могли принять участие в обращении ГКО только через уполномоченных дилеров на рынке ГКО (это – банки, списки которых не трудно раздобыть). Однако среди банков разворачивается борьба за частного вкладчика, поэтому есть надежда, что в недалеком будущем всем желающим станут, доступны услуги официальных дилеров по операциям с ГКО.

( 4этап проекта: «Лучший вклад на сегодня».

Демонстрация результатов исследования. Защита проектов.)

 

 

Модуль занятия «Проценты в мире профессий»

Решение задач

1. Предприниматель покупает кондитерские изделия по опто­вой цене 96 рублей и продает их в розницу с надбавкой в 30 %. Ка­кова розничная цена?

Решение. 1,3-96= 124,8 (р.)

Ответ: 124,8 р.

2.                  Каждую сторону квадрата увеличили на 20 %. На сколько процентов увеличилась площадь квадрата?

Ответ: на44%.

3.                   На сколько процентов увеличится объем куба, если его реб­ро увеличить на 10 %.

      Ответ: 33,1 %.

4.                     Владелец дискотеки имел стабильный доход. В погоне за прибылью он увеличил цену на билеты на 25 %. Количество посе­тителей резко уменьшилось, и он стал нести убытки. Тогда он вер­нулся к первоначальной цене билетов. На сколько процентов вла­делец дискотеки снизил новую цену билетов, чтобы она стала пер­воначальной?

Ответ: 20%.

5.                   После уплаты всех налогов, которые в сумме составили 30 % от дохода, предприниматель оставил себе на законном основании 35 000 р. Какова была величина чистого дохода предпринимателя?

Ответ: 50 000 р.

6.                    По расчетам предпринимателя предприятие принесет 15 % прибыли. Какую прибыль можно получить, затратив 200 000 р.?

Ответ: 30 000р.

7.                   Завод выпускает 300 изделий в месяц. В связи с модерниза­цией производства завод стал выпускать на 20 % изделий больше. На сколько изделий в месяц увеличится выпуск продукции?

О т в е т: 60 изделий.

8.                   В одном из городов часть жителей умеет говорить только по-грузински, часть - только по-русски. По-грузински говорят 85 % всех жителей, а по-русски - 75 %. Сколько процентов всех жителей говорят на обоих языках?

Ответ: 60%.

9.                   Ученик прочитал в первый день 15 % книги, что составило 60 страниц, во второй день он прочитал 200 страниц. Сколько страниц ему осталось прочитать?

Ответ: 140 страниц.

10.               Сравните числа аи в, если 3 % числа а равны 27, а 5 % чис­ла в равны 45.

Ответ: а = в - 900.

11.               В одном магазине на товар установили цену 200 р., а в дру­гом аналогичный товар стоит 180 р.

а)        На сколько процентов в первом магазине цена на товар вы­ше, чем во втором?

б)       На сколько процентов во втором магазине цена ниже, чем в первом?

Ответ: а)~ 11,1 %;б)на10%.

12.                 Определите, какую массу картофеля (сырья) нужно взять для получения 120 кг полуфабриката, если потери при холодной обработке составляют 20 % массы сырья.

Ответ: 150 кг.

13.               В двух бочках было воды поровну. Количество воды в пер­вой бочке сначала уменьшили на 10 %, а затем увеличили на 10 %. Количество воды во второй бочке сначала увеличили на 10 %, а затем уменьшили на 10 %. В какой бочке стало больше воды?

Ответ: воды в бочках осталось поровну.

14.               Цена на бензин в первом квартале увеличилась на 20 %, а во втором - на 30 %. На сколько процентов увеличилась цена на бен­зин за два квартала?

Ответ: на56%.

15.               За 3 года население города увеличилось с 2 000 000 до 2 315 250 человек. Найдите годовой прирост населения в процентах.

Ответ: 5 %.

16.               Зарплату рабочему повысили на 10 %, а через год еще на 20 %. На сколько процентов повысилась зарплата по сравнению с перво­начальной?

Ответ: на 32 %.

17.                Производительность труда на заводе снизилась на 20 %. На сколько процентов надо ее теперь повысить, чтобы достигнуть первоначальной?

О т в е т: на 25 %.

18.                После реконструкции завод увеличил выпуск продукции на 30 %. Спустя некоторое время выпуск продукции увеличился на 10 %, а после замены оборудование еще на 15 %. На сколько про­центов увеличился первоначальный выпуск продукции?

Ответ: на61,45 %.

19.               Выпуск продукции завода за 4 года увеличился в 16 раз. На сколько процентов в среднем увеличился выпуск продукции за ка­ждый год по сравнению с предыдущим годом?

Ответ: 100%.

20.               Саша за весну похудел на 20 %, за лето поправился на 30 %, за осень похудел на 20 %, за зиму поправился на 10 %. Как изме­нился его вес?

Ответ: похудел на 8,48 %.

21.                В ходе утверждения городского бюджета были сокращены на 20 % планируемые ассигнования на социальные нужды. Какую сумму предполагалось выделить на социальные нужды первона­чально, если в окончательном варианте бюджета эта статья расхо­дов составила 2,5 млн р.?

Ответ: 3,125 млн р.

22.                Цена входного билета на стадион была 18 р. После сниже­ния входной платы число зрителей увеличилось на 50 %, а выручка выросла на 25 %. Сколько стал стоить билет после снижения?

Ответ: 15 р.

23.               В этом году тарифы на услуги лодочной станции оказались на 20 % ниже, чем в прошлом году. Можно ли утверждать, что в прошлом году тарифы были на 20 % выше, чем в нынешнем году?

Ответ: нет.

24.                 Стоимость проезда в городском автобусе составляла 5 р. В связи с инфляцией она возросла на 200 %. Во сколько раз повыси­лась стоимость проезда в автобусе?

О т в е т: в 3 раза. 

25.                    За несвоевременное выполнение договорных обязательств сотрудник фирмы лишается 25 % месячного оклада и, кроме того, за каждый просроченный месяц к штрафу прибавляется 5 % месяч­ного оклада. Оклад сотрудника 10 тыс. р. В каком размере он дол­жен заплатить штраф при нарушении сроков на 5 месяцев?

Ответ: 5 тыс. р.

26.                 Занятия ребенка в музыкальной школе родители оплачива­ют в Сбербанке, внося ежемесячно 250 р. Оплата должна произво­диться до 15 числа каждого месяца, после чего за каждый просро­ченный день начисляется пеня в размере 4 % от суммы оплаты за­нятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю?

Ответ: 320 р.

27.                Во время распродажи масляные краски для рисования стои­мостью 213 р. за коробку продавали на 19 % дешевле. Сколько примерно денег сэкономит художественная студия, если она купит партию в 150 коробок?

Ответ; около 6000 р.

28.                Два магазина торгуют одним и тем же товаром. В первом из них цены на 10 % ниже, но и количество проданных изделий в день на 10 % больше. В каком из этих магазинов выручка за день больше?

Ответ: во втором.

29.                 На весенней распродаже в одном магазине шарф стоимо­стью 350 р. уценили на 40 %, а через неделю еще на 5 %. В другом магазине шарф такой же стоимости уценили сразу на 45 %. В каком магазине выгоднее купить шарф?

О т в е т: во втором.

30.                  На сезонной распродаже в марте месяце зимние сапоги можно купить за 1875 р., скидка на них составила 25 % от первона­чальной стоимости. Через месяц сапоги подешевели еще на 20 %. Сколько денег сэкономит человек от первоначальной стоимости сапог, если купит их в апреле?

Ответ: 1000р.

31.                 Арендатор отдела в магазине забыл вовремя оплатить арен­ду за место. Определите размер пени за каждый просроченный день, если за 20 дней просрочки сумма платежа увеличилась с 10 до 14 тыс. р.

Ответ: 2 %.

32.                  Какой должен быть первоначальный капитал, чтобы при начислении 5 % в месяц получить через полгода 10 тыс. р.?

Ответ: 7463 р.

33.                 Какой должна быть процентная ставка в банке, чтобы каж­дые три года капитал увеличивался в четыре раза?

Ответ: 59%.

34.                  Банк обещает вкладчикам удвоить их сбережения за пять лет, если они воспользуются вкладом «накопление» с годовой про­центной ставкой 16 %. Проверьте, выполнит ли банк свое обяза­тельство.

О т в е т: да.

35.                  Банк «Диалог-Оптима» осуществляет денежные переводы. Минимальная сумма перевода 50 р., максимальная - 300 р. С сум­мы перевода банк берет 1,5 % за оказание своих услуг. На сколько в процентном отношении возьмут больше с человека, сделавшего пере­вод на максимальную сумму, чем с того, кто сделал перевод на 50 р.?

Ответ: на 500%.

36.                 За каждый из девяти первых месяцев года цены вырастали на 25 %, а за каждые из трех следующих месяцев на х %. Найдите х, если в целом за год цены выросли в восемь раз.

Ответ: 2,4%.

37.                Каким должен быть начальный вклад, чтобы при ставке 4 % в месяц он увеличился за 8 месяцев до 33 000?

Ответ: 25 000 р.

38.                Банк выплачивает вкладчикам каждый год 8 % от внесенной суммы. Клиент сделал вклад в размере 200 000 р. Какая сумма бу­дет на его счете через 5 лет, через 10 лет?

Ответ: 280 000 р., 360 000 р.

39.                Вкладчик открыл счет в банке, внеся 2000 р. на вклад, годо­вой доход по которому составляет 12 %, и решил в течение шести лет не брать процентные начисления. Какая сумма будет лежать на его счете через год, через два, через 6 лет?

Ответ: 3947 р. 65 к.

40.                Некто не доверяет банкам и хранит сбережения дома. Круп­ная премия пролежала дома до лета. За это время цены на товары выросли в среднем на 50 %. На сколько процентов уменьшилась покупательная способность отложенных денег?

Ответ: на 33%.

 

41.                 Сколько граммов воды можно выпарить из 80 г 6 %-го рас­твора соли, чтобы получить раствор, содержащий 10 % соли?

Ответ: 32 г.

42.                 Имеется два кислотных раствора: один 20 %, другой 30 %. Взяли 0,5 л первого и 1,5 л второго раствора и образовали новый раствор. Какова концентрация кислоты в новом растворе?

Ответ: 27,5%.

43.                 Смешали 300 г 50 %-го и 100 г 30 %-го раствора кислоты. Определите процентное содержание кислоты в полученной смеси.

Ответ: 45%.

44.                 Сколько чистой воды надо добавить к 300 г морской воды, содержащей 4 % соли, чтобы получить воду, содержащую 3 % соли?

Ответ: 100 г.

45.                  Имеются две смеси апельсинового и ананасового соков. Первая смесь содержит 40 % апельсинового сока, а вторая - 80 %. Сливаются р л первой смеси и д л второй, в результате получается 20 л смеси, содержащей 70 % апельсинового сока. Определите рид.

Ответ:/? = 5 л, д = 15 л.

46. Сколько граммов воды надо добавить к 50 г раствора, со­держащего 8 % соли, чтобы получить 5 % раствор?

Ответ: 30 г.

47. Сколько граммов 30 %-го раствора надо добавить к 80 г 12 %-го раствора этой же соли, чтобы получить 20 %-й раствор соли?

О т в е т: 64 г.

47.                    Если смешать 8 кг и 2 кг растворов серной кислоты разной концентрации, то получим 12 %-й раствор кислоты. При смешива­ний двух одинаковых масс тех же растворов получим 15 %-й рас­твор. Определите первоначальную концентрацию каждого раствора.

Ответ: 10 % и 20 % раствор

48.                    Даны два куска с различным содержанием олова. Первый,- массой 300 г, содержит 20 % олова. Второй, массой 200 г, содержит 40 % олова. Сколько процентов олова будет содержать сплав, по­лученный из этих кусков?

Ответ: 28%.

49.                   Имеется два куска сплава олова и свинца, содержащие 60 % и 40 % олова. По сколько граммов от каждого куска надо взять, что­бы получить 600 г сплава, содержащего 45 % олова?

Ответ: 150 г; 450 г.

50.                     Торговец продает орехи двух сортов: одни по 90 центов, другие по 60 центов за килограмм. Он хочет получить 50 кг смеси по 72 цента за килограмм. Сколько для этого потребуется орехов каждого сорта?

51.                      О т в е т: 20 кг и 30 кг. Объем строительных работ увеличивается на 80 %. На сколько процентов нужно увеличить число рабочих, если произво­дительность труда будет увеличена на 20 %?

Ответ: на60%.

52.                     Рабочий в феврале увеличил производительность труда по сравнению с январем на 5 %, а в марте увеличил ее снова по срав­нению с предыдущим месяцем на 10 %. Сколько деталей изготовил рабочий в марте, если в январе изготовил 200 деталей?

О т в е т: 231 деталь.

53.                    Число коров на одной молочной ферме на 12,5 % меньше, чем на другой, но средний удой каждой коровы на 8 % выше. На какой ферме получают молока меньше и на сколько процентов?

Ответ: на 5,5 %.

54.                     В бассейн проведена труба. Вследствие ее засорения при­ток воды уменьшился на 60 %. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна?

Ответ: на 150%.

55.                     Только что добытый каменный уголь содержит 2 % воды. После некоторого времени он впитывает в себя еще некоторое ко­личество воды и содержит уже 15 % ее. На сколько увеличится при этом вес 27,75 т только что добытого каменного угля?

Ответ: 3,9т.

56.                     Перерабатывая цветочный нектар в мед, пчелы освобож­дают его от значительной части воды. Нектар содержит 70 % воды, а мед - 16 %. Сколько килограммов нектара надо переработать для получения 1 кг меда?

Ответ: 2,8 кг.

57.                       На овощную базу привезли 10 тонн крыжовника, влаж­ность которого 99 %. За время хранения на базе влажность умень­шилась на 1 %. Сколько тонн крыжовника теперь хранится на базе?

58.                     О т в е т: 5 т. В свежих грибах было 90 % воды. Когда их подсушили, то они стали легче на 15 кг при влажности 60 %. Сколько было све­жих грибов?

О т в е т: 90 кг.                       

 

Деловая  игра

«ПРОЦЕНТЫ В СОВРЕМЕННОЙ ЖИЗНИ»                       

                   Цели игры: ориентировать учащихся на прикладное при­менение математических знаний в профессиональной деятельно­сти; в неформальной обстановке произвести диагностику качества знаний учащихся по данной теме.

Учебно-воспитательные задачи:

1. Создать условия, в которых учащиеся могут испытать себя как будущего профессионала, проявить свои деловые качества: умение «презентовать» себя на рынке труда, умение руководить коллективом, инициативность, выносливость, смелость.

2.                Способствовать развитию умений применить свои знания в нестандартных ситуациях, развитию творческих и коммуникатив­ных способностей учащихся.

3.  Стимулировать интерес к предмету, развивать чувство соли­дарности и здорового соперничества.

Форма проведения: урок - деловая игра.

ПЛАН ПРОВЕДЕНИЯ

1.  Вступительное слово ведущего.

2.               Выполнение предложенных заданий.

3.  Проверка заданий и подготовка презентации команд.

4.              Просмотр презентации каждой команды.

5.  Подведение итогов.

Подготовка:

Игра проводится на занятии  как урок повторения темы «Проценты». В игре принимает участие 20 человек: 5 групп по 4 человека. Каждая группа заранее выбирает себе тему для про­центных вычислений: «Распродажа», «Тарифы», «Штрафы», «Бан­ковские операции», «Голосование». Роли всех участников распре­деляются до игры и объясняются правила.

После распределения ролей между учениками готовятся бланки заданий для каждой группы, печатаются названия групп и каждому участнику делается эмблема с его именем и ролью.

 

1-я группа «Распродажа»:

1)  Менеджер магазина (проверяющий) -

2)             Продавец антикварного отдела (решает задачу) -

3)             Продавец обувного отдела (решает задачу) -

4)             Покупатель (роль второго плана) –

1) Аудитор - проверяющий; -

2) Сотрудник коммунального отдела (решает задачу) -

2-я группа «Тарифы»:

1)  Аудитор (проверяющий) -

2)             Сотрудник коммунального отдела (решает задачу) -

3)             Продавец мобильных телефонов (решает задачу) -

4)            Квартиросъемщик (роль второго плана) -

3-я группа «Штрафы»:

1)  Старший кассир (проверяющий) -

2)              Кассир 1 (решает задачу) -

3)              Кассир 2 (решает задачу) -

4)             Водитель машины (роль второго плана) —

4-я группа «Банковские операции»:

1) Управляющий (проверяющий) -

2)            Бухгалтер (решает задачу) —

3)             Экономист (решает задачу) -

4)            Вкладчик (роль второго плана) -

5-я группа «Голосование»:

1)  Председатель счетной комиссии (проверяющий) -

2)              Участник ученического совета (решает задачу) -

3)              Член избирательной комиссии (решает задачу) -

4)             Избиратель (роль второго плана) -

Оформление кабинета.

Перед началом игры расставляется мебель в классе, на столы ставятся таблички с названием команд, кладутся калькуляторы, ручки, участники прикрепляют себе эмблемы. На доске написано название игры, доска украшена рисунками и надписями по теме.

Правила игры.

I. Вступительное слово ведущего.

Все игроки занимают свои места. Ведущий сообщает цели иг­ры, кратко напоминает её правила. Проверяющие каждой команды получают от ведущего карточки с заданиями для своей команды.

Задачи команды:

-          быстро и качественно решить задачи;

-          качественно осуществить контроль, т. е. произвести проверку решения задачи;

-          презентовать свою группу (проявить артистизм).

 

II.         Выполнение предложенных заданий.

По сигналу начинается решение поставленных задач, все игро­ки команды решают отдельно друг от друга. Но по желанию игрок второй роли может помогать своей команде. Все бланки с реше­ниями подписываются игроками.

Ведущий проходит по классу и делает пометки.

Задания для команд

Бланки 1-й группы «Распродажа».

Менеджер магазина

Задача №  1.1. Антикварный магазин  приобрел  старинный предмет за 30 тыс. р. и выставил его на продажу, повысив цену на цену на 60 %. Но этот предмет был продан лишь через неделю, когда магазин снизил его новую цену на 20 %. Какую прибыль получил магазин при продаже антиквар­ного предмета? Задача № 1.2. На сезонной распродаже магазин снизил цены на обувь сначала на 24 %, а потом ещё на 10 %. Сколько рублей можно сэкономить при покупке кроссовок, если до снижения цены они стоили 593 р.?

Продавец антикварного отдела

Задача № 1.1. Антикварный магазин приобрел старинный предмет за 30 тыс. р. и выставил его на продажу, повысив цену на 60 %. Но этот предмет был продан лишь через неделю, когда магазин снизил его новую цену на 20 %. Какую прибыль получил магазин при продаже антиквар­ного предмета?

Продавец обувного отдела

Задача № 1.2. На сезонной распродаже магазин снизил цены на обувь сначала на 24 %, а потом ещё на 10 %. Сколько рублей можно сэкономить при покупке кроссовок, если до снижения цены они стоили 593 р.?

Покупатель

Вы любите заниматься спортом и старинные вещи, а также по­сещать магазины во время распродажи. Вам примерно 40 лет. Зайдя в магазин на распродажу, обратитесь за советом к ме­неджеру: «Где дешевле приобрести антикварную вещь и крос­совки?» Потом у продавцов поинтересуйтесь: «Сколько же вы получили прибыли от моей покупки?» и «Сколько рублей я сэкономлю на кроссовках?».

Бланки 2-й группы «Тарифы».

Аудитор

Задача № 2.1. В начале года тариф на электроэнергию состав­лял 40 к. за 1 кВт-ч. В середине года он увеличился на 50 %, а в конце года - ещё на 50 %. Как вы считаете, увеличился ли тариф на 100 %, менее чем на 100 %, более чем на 100 %?

Задача № 2.2. Тарифы для мобильных телефонов зависят от систем оплаты. В 2000 г. тарифы оплаты по системе К и М были одинаковыми, а в следующие три года последо­вательно либо увеличивались, либо уменьшались (см. таблицу). Сравните тарифы в 2003 г.

 

 

Тарифы	Годы
	2011	2012	2013
По системе К	Увеличен на 10%	Уменьшена 3%	Уменьшен на 3%
По системе М	Уменьшен на 5%	Увеличена 3%	Увеличена 4%

 

Сотрудник коммунального отдела

Задача № 2.1. В начале года тариф на электроэнергию состав­лял 40 к. за 1 кВт-ч. В середине года он увеличился на 50 %, а в конце года - ещё на 50 %. Как вы считаете, уве­личился ли тариф на 100 %, менее чем на 100 %, более чем на 100%?

Продавец мобильных телефонов

Задача № 2.2. Тарифы для мобильных телефонов зависят от систем оплаты. В 2000 г. тарифы оплаты по системе К и М были одинаковыми, а в следующие три года последо­вательно либо увеличивались, либо уменьшались (см. таблицу). Сравните тарифы в 2003 г.

 

 

Квартиросъемщик

Вы следите за изменением цен, и вас заинтересовало повыше­ние тарифов на электроэнергию, а также вы хотите перейти на новый тариф сотовой связи. Вы молоды. Обратитесь сначала к сотруднику коммунального отдела: «Как вы считаете, тариф на
электроэнергию увеличился менее чем на 100 %?». Затем обратитесь к продавцу мобильных телефонов: «Я был на тарифе К, вот не знаю, остаться на нем или перейти на другой. Посоветуйте».  

Бланки 3-й группы «Штрафы»

Старший кассир

Задача № 3.1. Если водитель не прошел техосмотр автомаши­ны, то сотрудник ГИБДД должен оштрафовать его на 1/2 минимальной оплаты труда. Стоимость прохождения техосмотра составляет примерно 150 рублей, а размер минимальной заработанной платы 500 рублей. На сколь­ко процентов штраф превышает стоимость техосмотра, если при оплате штрафной квитанции в банке с водителя возьмут 3 % за услуги банка?

Задача № 3.2. Занятия ребенка в музыкальной школе родители оплачивают в Сбербанке, внося ежемесячно 250 р. Оплата должна производиться до 15-го числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4 % от суммы оплаты занятий за один ме­сяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю?

Кассир 1

Задача № 3.1. Если водитель не прошел техосмотр автомаши­ны, то сотрудник ГИБДД должен оштрафовать его на 1/2 минимальной оплаты труда. Стоимость прохождения техосмотра составляет примерно 150 рублей, а размер минимальной заработанной платы 500 рублей. На сколь­ко процентов штраф превышает стоимость техосмотра, если при оплате штрафной квитанции в банке с водителя возьмут 3 % за услуги банка?

Кассир 2

Задача № 3.2. Занятия ребенка в музыкальной школе родители оплачивают в Сбербанке, внося ежемесячно 250 р. Оплата должна производиться до 15-го числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4 % от суммы оплаты занятий за один ме­сяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю?

Водитель машины

Вы хороший водитель, но вот техосмотр не прошли, вместо та­лона у вас висит календарик, вот вас и оштрафовали. Обрати­тесь к кассиру 1: «Вы не могли бы посчитать, на сколько про­центов я заплачу штрафа больше от суммы техосмотра». Затем вы вспоминаете, что забыли заплатить за занятия ребенка в му­зыкальной школе. Обратитесь к кассиру 2: «Я просрочил опла­ту на неделю, сколько же теперь придется заплатить?».

Бланки 4-й группы «Банковские операции»

Управляющий

Задача № 4.1. За хранение денег Сбербанк начисляет вкладчику 8 % годовых. Вкладчик положил на счет в банке 5000 р. и решил в течение пяти лет не снимать деньги со счета и не брать процентные начисления. Сколько денег будет на счету вкладчика через год, через пять лет?

Задача № 4.2. На данной диаграмме изображен рост вклада в Сбербанке. С помощью диаграммы определите величину первоначального вклада и процентную ставку. Запишите формулу увеличения вклада и вычислите, какую сумму получит вкладчик через 12 лет?

Бухгалтер

Задача № 4.1. За хранение денег Сбербанк начисляет вкладчику 8 % годовых. Вкладчик положил на счет в банке 5000 р. и решил в течение пяти лет не снимать деньги со счета и-не брать процентные начисления. Сколько денег будет на счету вкладчика через год, через пять лет?

Экономист

Задача № 4.2. На данной диаграмме изображен рост вклада в Сбербанке. С помощью диаграммы определите величину первоначального вклада и процентную ставку. Запишите формулу увеличения вклада и вычислите, какую сумму получит вкладчик через 12 лет?

Вкладчик

Вы любите делать вклады, покупать ценные бумаги. Вы — «но­вый русский». В данном банке у вас два счета. Обратитесь к бухгалтеру с вопросом: «Сколько у меня будет денег через год, через пять лет, если не брать процентные начисления?». А к эко­номисту: «Вы не подскажете, я не помню, какую сумму первона­чально положил на счет и сколько будет через 12 лет на счете».

Бланки 5-й группы «Голосование»

Председатель счетной комиссии

Задача № 5.1 В 2004 году в выборах Президента РФ на изби­рательном участке № 356 приняло участие 56 % избира­телей от общего числа 2844 человека. За Путина В. В. от­дали голоса 1069 пришедших на выборы избирателей, за Ирину Хакамаду проголосовало 78 человек. Выборы счи­таются состоявшимися. Кто из кандидатов   победил на этом участке (победитель должен преодолеть 50 % барь­ер) и на сколько процентов обогнал своего соперника?

Задача № 5.2. Из 550 учащихся школы в референдуме по во­просу о введении ученического совета участвовали 88 % учащихся. На вопрос референдума 75 % принявших уча­стие в голосовании ответили «Да». Какой процент от числа всех учащихся школы составили те, кто ответил положительно?

Член избирательной комиссии

Задача № 5.1. В 2004 году в выборах Президента РФ на изби­рательном участке № 356 приняло участие 56 % избира­телей от общего числа 2844 человека. За Путина В. В. от­дали голоса 1069 пришедших на выборы избирателей, за Ирину Хакамаду проголосовало 78 человек. Выборы счи­таются состоявшимися. Кто из кандидатов победил на этом участке (победитель должен преодолеть 50 % барь­ер) и на сколько процентов обогнал своего соперника?

Участник ученического совета

Задача № 5.2. Из 550 учащихся школы в референдуме по во­просу о введении ученического совета участвовали 88 % учащихся. На вопрос референдума 75 % принявших уча­стие в голосовании ответили «Да». Какой процент от числа всех учащихся школы составили те, кто ответил положительно?

Избиратель

Вы очень любите ходить на всякие митинги, собрания. Вам лет 70. Вот и сейчас после выборов президента вас очень интересу­ет вопрос: «Кто из кандидатов победил на вашем избиратель­ном участке и на сколько процентов опередил своего соперни­ка?». Обратитесь с этим вопросом к члену избирательной ко­миссии. Но вы также хотите узнать, как прошел школьный референдум вашего внука: «Сколько же процентов учащихся проголосовало за введение ученического совета?». Обратитесь с этим вопросом к участнику ученического совета.

III.        Проверка заданий и подготовка презентации команд

Затем проверяющие забирают решения игроков и сравнивают со своим решением, т. е. осуществляют проверку, исправляя ошиб­ки, если они есть. И в специальной графе на своем бланке делают пометки. А в это время остальные члены команды готовят презен­тацию своей группы. То есть им нужно оживить своих героев и свои задания. Придумать способ общения между действующими лицами, проговорить условие задачи и её ответ, примерить на себя роль конкретного человека в жизненной ситуации.

Ведущий проходит по классу и делает пометки.

IV. Просмотр презентации каждой команды.

При просмотре презентации оценивается артистизм каждой ко­манды, как они смогли реализовать себя в данной роли, как про­явили свои деловые качества, на каком уровне проходило общение между членами команд.

Ведущий делает пометки.

V.        Подведение итогов .

В бланке ведущего уже зафиксировано определенное количест­во баллов каждой команды, но он может посоветоваться со зрите­лями по последнему этапу. После того как произведены все под­счеты, ведущий объявляет результат игры. Побеждает команда, набравшая наибольшее количество баллов.

Оценки учитель выставляет каждому игроку отдельно. В жур­нал выставляются только хорошие отметки, а действиям некоторых учащихся дается устная оценка или какие-то рекомендации.