Производная

Конспект урока

Алгебра и начала анализа, 11 класса.

Урок №14. Геометрический смысл производной.

Перечень вопросов, рассматриваемых в теме

1) Геометрический смысл производной;

2) Алгоритм нахождения касательной к графику функции в точке;

3) Сравнение производных заданной функции по ее графику в различных точках.

Глоссарий по теме

Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Напомним, что графиком линейной функции у=кх + b является прямая.

Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.

Если k>0, то 0<α< π/2, в этом случае функция возрастает

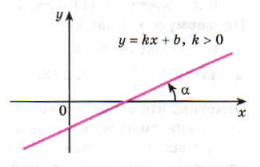
Если k<0, то - π/2<α<0, в этом случае функция убывает

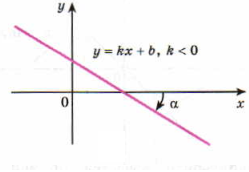
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

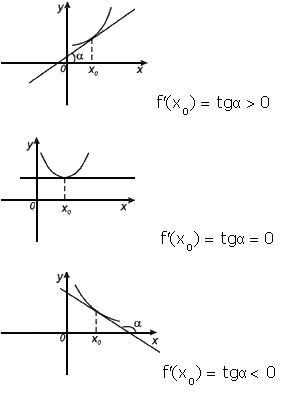
Рассмотрим график функции y = f ( x ):

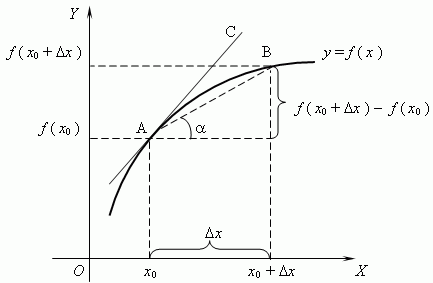
Из рисунка видно, что для любых двух точек A и B графика функции: f(x0+Δx)/f(x0)Δx=tgα, где  - угол наклона секущей AB. 

Таким образом, разностное отношение равно угловому коэффициенту секущей. 

Если зафиксировать точку A и двигать по направлению к ней точку B, то Δx неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. 

Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.

Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

Уравнение касательной к графику функции y=f(x) в точке x₀:

Примеры и разбор решения заданий тренировочного модуля

№1. Составить уравнение касательной к графику функции y=x+e^-2x, параллельной прямой y=-x

Решение:

Угловой коэффициент касательной равен значению производной в точке касания x₀. Т.к. касательная параллельна прямой y=-x, значит ее угловой коэффициент равен –1. Таким образом, f'(x₀) = -1.

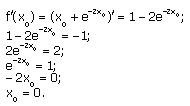
Уравнение касательной:

Уравнение касательной: y=1-1(x-0) = 1-x

Ответ: y=1-x.

№2. На параболе у=х²-2х-8 найти точку М, в которой касательная к ней параллельна прямой 4х+у+4=0.

Решение:

Определим угловой коэффициент касательной к параболе у=х²-2х-8:

k =у'=(х²-2х-8)'=2х-2.

Найдем угловой коэффициент прямой 4х+у+4=0:

у=-4х-4, k =-4.

Касательная к параболе и данная прямая по условию параллельны. Следовательно, их угловые коэффициенты равны, т.е.

2х-2=-4;

х=-1 – абсцисса точки касания.

Ординату точки касания М вычислим из уравнения данной параболы у=х²-2х-8, т.е.

у(-1)=(-1)²-2(-1)-8=-5, М(-1;-5).

Ответ: М(-1;-5).