Производная функция

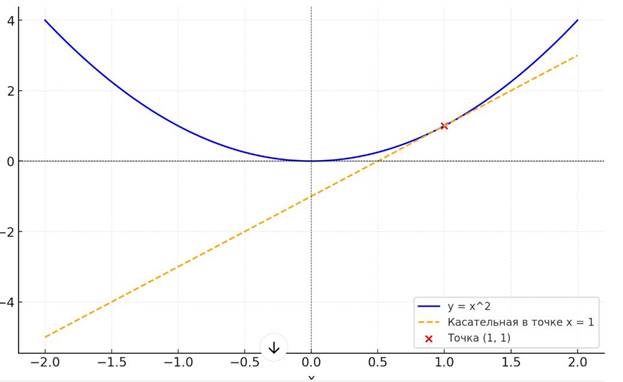
Производная  функция

Производная функция — это функция изменения скорости в каждом месте. Если представить функцию графика как дорогу, то производная показывает, действительно крутой у каждого подъема или спуска на месте.

Формальное определение

Производная функцияф(х)ф(х)ж ( х )ввашейх0х_0х0​— это угловой коэффициент касательной, отображаемый функцией графика в этом помещении. Она определяется как предел изменения значений функции, приводящей аргумент:

ф′(х0)=лим⁡Δх→0ф(х0+Δх)−ф(х0)Δх.f'(x_0) = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}.ф′( х0​)=Δx → 0​лим​Δ хж ( х0​+Δ х )−ж ( х0​)​.

Проще говоря:ф(х)=х2f(x) = x^2ж ( х )=х2

For functionф(х)=х2f(x) = x^2ж ( х )=х2:

• Производственнаяф′(х)=2хf'(x) = 2xф′( х )=2 хЭто означает, что в каждой точке функция изменения скорости зависит от значения.ххх.

Пример в вашейх=1х = 1х=1:

• Значение функции:ф(1)=12=1ф(1) = 1^2 = 1ж ( 1 )=12=1.
• Значение производной:ф′(1)=2⋅1=2f'(1) = 2 \cdot 1 = 2ф′( 1 )=2⋅1=2. Это означает, что график поднимается со скоростью 2 в этом месте.

На графике:

• Синяя линия — это функция графикау=х2у = х^2у=х2.
• Оранжевая пунктирная линия — это касательная к графику в пункте назначениях=1х = 1х=1.
• Точка касания выделена красным. Наклон касательной представляет собой результат производной.

Если есть вопросы, готов объяснить подробнее! ​