Государственное профессиональное образовательное учреждение «Шилкинский многопрофильный лицей"

ИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ

ПРОИЗВОДНАЯ

В ФИЗИКЕ И ТЕХНИКЕ

Выполнил студент группы ЭТП 8-23

Николаев Михаил

Руководитель

Екатерина Владимировна Усова

Работа допущена к защите «_____» _____________________________ 202__г.

Подпись руководителя проекта ________ (_____________________________)

Шилка
2024

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ…………………………………………………………..………………............ ..3

ГЛАВА I ТЕОРЕТИЧЕСКАЯ  ЧАСТЬ                                                               

1.1  ИСТОРИЧЕСКИЕ СВЕДЕНИЯ…………………………..……….………………….…...5

1.2  ПОНЯТИЕ «ПРОИЗВОДНАЯ»………………………..…………….………………….…7

ГЛАВА II. ПРАКТИЧЕСКАЯ ЧАСТЬ

2.1. ОСНОВНЫЕ ПОНЯТИЯ ПРОИЗВОДНОЙ………………………………………..….   9

2.2. ОБЛАСТЬ  ПРИМЕНЕНИЯ  ПРОИЗВОДНОЙ…………….………………………......10

2.3. ПРОИЗВОДНАЯ В РЕШЕНИИ ФИЗИЧЕСКИХ  ЗАДАЧ………….………….……. .12

ЗАКЛЮЧЕНИЕ……….…………………………………………………….……………….. .14

СПИСОК ИСПОЛЬЗУЕМЫХ  ИСТОЧНИКОВ………………….……….………………...15

ВВЕДЕНИЕ

«Все сведения о природных телах и их свойствах должны содержать точные указания на число, вес, объем, размеры… Практика рождается только из тесного соединения физики и математики»

Ф.Бекон

Тема "Производная функции" считается одной из самых сложных в курсе математики. Однако, сложность этой темы заключается в непонимании учащимися её нужности. Область применения производной остается непознанной большинством людей, которые  не имеют полного представления о производной и обширной области её применения.

В  курсе математики производная изучается на втором курсе. Нам предстоит решать задачи, которые имеют не только математический, но и прикладной смысл. Много задач по нахождению производной встречается и на экзамене. И для того, чтобы дойти до самой сути этой большой темы, я решил уже на 1 курсе серьёзно изучить область применения производной.

         Актуальность: производная широко используется в различных областях деятельности человека, поэтому умение прогнозировать, решать, имеет огромное значение в практической деятельности.

         Цель проекта: изучить вопрос  применения производной для решения задач по  физике и технике, углубить и расширить знания по теме «Производная»

Задачи:

1.            Установить связь физических величин с понятием производной.

2.            Рассмотреть использования механического смысла производной для решения прикладных задач.

Гипотеза: производная – это не исключительно математический инструмент: она также позволяет решать задачи в области физики и техники.

Объект исследования: прикладные задачи практического содержания

Предмет исследования: методы решения задач с использованием производной

Продукт проекта: письменная работа

наука

Глава I   теоретическая часть

1.1 Исторические сведения

Производная - одно из фундаментальных понятий математики. Она возникла в 18 веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь для  определения скорости прямолинейного движения и построения касательной к кривой. Независимо друг от друга Исаак Ньютон(1643-1727) и Готфрид Лейбниц(1646-1716)  разработали теорию дифференциального исчисления.

Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.Ньютон в основном опирался на физическое представление о мгновенной скорости движения, считая его очевидным и сводя к нему другие случаи производной

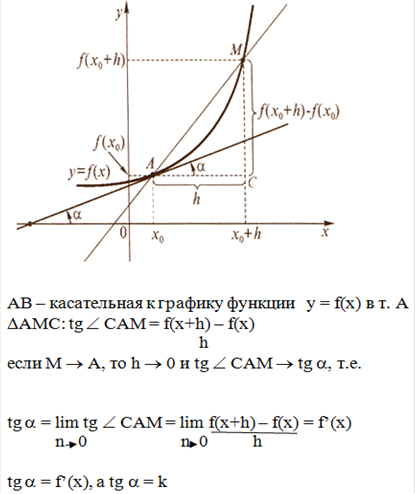
                                       рис. 1

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл.

В самом деле, для любой функции y=f (x) в системе координат, в её области определения можно построить график. Если взять значение  на оси абсцисс то, в соответствие этому значению можно найти на графике значение функции. В этой точке также может быть построена касательная, образующая с положительным направлением оси абсцисс угол α такой, что

(см. рис. 1)

         Задолго до открытия Ньютоном и Лейбницем  греческий ученый  Архимед (287 до н.э. - 212 до н. э) не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.

Эпизодически понятие касательной встречалось в работах итальянского математика И. Тартальи (1499-1557).

Понятие производной встречается в учениях Г. Галилея (1564-1642) ,Р. Декарта (1596-1650), французского математика Ж. Роберваля (1602-1675), английского учёного Д. Грегори (1638-1675), в работах И. Барроу (1630-1677).

Большой вклад в изучение дифференциального исчисления внесли Лопиталь (1661-1704), Бернулли (1744-1807), Лагранж (1736-1813), Гаусс (1777-1855), Коши (1789-1857). Необходимо сказать, что ни Ньютон, ни Лагранж не дали четкого определения производной. Впервые определение производной было сформулировано Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах математического анализа.

1.2 ПОНЯТИЕ «ПРОИЗВОДНАЯ»

Понятие производной находит большое применение в различных областях науки и техники. Так что же такое производная?

«Производная» – это то, что «произведено» какой-то функцией. Простой пример: Яйцо – это производная курицы. Понятие производной довольно трудное, т.к. основано на абстрактном восприятии. Мы рассмотрим ситуацию, известную нам из повседневной жизни.

Представим себе прямую дорогу, проходящую по холмистой местности. То есть она идет то вверх, то вниз, но вправо или влево не поворачивает. Если ось ОХ направить вдоль дороги горизонтально, а ОУ – вертикально, то линия дороги будет очень похожа на график некоторой  непрерывной функции. Где ось ОХ – путь, а ось ОУ – время.

Двигаясь вперед по такой дороге, мы также движемся вверх или вниз.

Рассмотрим график этого движения. На оси ОУ – время t, по оси ОХ – пройденный путь s(t). Как узнать, с какой скоростью  движется автомобиль?  Надо пройденный путь разделить на время

 Vср. = Δs : Δt

 Что является средней скоростью.

 Если мы уменьшим отрезок времени до 0, что произойдет со скоростью? Представьте себе, на посту ГИБДД скорость отслеживается с помощью радара. В момент пересечения луча радара автомобилем на табло радара высвечивается цифры скорости. Будет ли она равна средней скорости (может да, а может, нет). Как можно назвать такую скорость? Мгновенной, т.к. мы рассматриваем скорость в какое-то мгновение.

И если среднюю скорость может найти даже пятиклассник, то определить мгновенную скорость в определенной точке под силу только человеку, знакомому с понятием производной. Именно она   дает точную информацию о движении в определенный момент времени и называется мгновенной скоростью.

Если отрезок времени стремится к 0, то скорость из средней превращается в мгновенную:

ГЛАВА II ПРАКТИЧЕСКАЯ ЧАСТЬ

2.1.                      ОСНОВНЫЕ ПОНЯТИЯ ПРОИЗВОДНОЙ

Производная функции это отношение приращения функции к приращению аргумента при бесконечно малом приращение аргумента.

Приращением в математике называют изменение. То, насколько изменился аргумент (x) при продвижении вдоль оси Ox, называется приращением аргумента и обозначается Δx. То, насколько изменилась значение функции (высота) при продвижении вперед вдоль оси Ox на расстояние Δx, называется приращением функции и обозначается Δf.

Итак, производная функции f(x)– это отношение Δf к Δx  при Δx→0. Обозначаем производную той же буквой, что и функцию, только со штрихом сверху справа: f'(x)  или просто f '

​Запишем формулу производной, используя эти обозначения:

             при Δx→0

Алгоритм  вычисления производной

Вычисление производной функции y=f(x) производится по следующей схеме:

1) Находим приращение функции на отрезке [x;x+∆x]:

∆y = f (х +х) - f (х).

2) Делим приращение функции на приращение аргумента:

3) Находим предел   , устремляя ∆х к нулю.

Переход к пределу мы будем записывать либо с помощью знака lim ,либо с помощью стрелки.

2.2.                      ОБЛАСТЬ  ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ

Понятие производной возникло как математическое описание скорости движения. Поэтому важнейшим приложением производной является вычисление скорости, а ещё говорят, что производная есть мгновенная скорость изменения функции, поэтому производная широко применяется в физике и технике. Приведём примеры:

1.Пусть материальная точка движется прямолинейно и её координата вычисляется по закону x(t), то скорость её движения равна:

V(t)=S’(t)

скорость движения точки равна производной от пути по времени

2. Ускорение есть производная скорости по времени (или вторая производная от пути по времени).

       a(t) = V’(t) илиa(t) = X’’(t)     

3. Сила. Рассмотрим работу, которую совершает сила F при перемещении по отрезку оси x.

F=A'(x). Сила есть производная работы по перемещению.

4.Ток. Сила тока является производной заряда по времени  I = q’(t),q-заряд, который переносится электрическим током, через поперечное сечение проводника за время t.

5. Линейная плотность. Линейная плотность неоднородного тонкого стержня-это производная массы по длине. Ρ(l)=m'(l). Неоднородность стержня означает, что его линейная плотность не является постоянной.

6.Теплоёмкость. Рассмотрим процесс нагревания какого-нибудь вещества и будем вычислять количество теплоты Q(T), которое необходимо, чтобы нагреть 1 кг этого вещества от 0^о до T^о (по Цельсию). Тогда, теплоёмкость – это производная теплоты по температуре.

C = Q’(T)

7.Мощность. Нам известно, что характеристика работы, определяющая её скорость по времени – это мощность. Мощность есть производная работы по времени:

N = A’(t)

8.Изменения объема. Если V(p) – закон изменения объёма жидкости от внешнего давления p, то производная V’(p) есть мгновенная скорость изменения объёма при внешнем давлении, равном p:

V_мгн = V’(p)       

2.3 РЕШЕНИЕ ФИЗИЧЕСКИХ ЗАДАЧ

Производная широко применяется при решении различных физических задач. Рассмотрим решение нескольких задач.           

1.Тело движется прямолинейно по закону x(t) = 3t² + 2t + 1, где x-координата (в метрах), t- время (в секундах). Найти скорость движения тела в момент времени t = 4 с.

Решение.

Так как скорость это 1-ая производная от координаты по времени, то

V(t) = x’(t);  V(t) = 6t + 2 ;

V(4) = 6 · 4 + 2 = 26 (м/с).   

Ответ: 26 м/с.

2.Для машины, движущейся со скоростью 30 м/с, тормозной путь определяется по формуле S(t) = 30t – 16t², где S(t) – путь в метрах, t – время торможения в секундах. В течении какого времени осуществляется торможение до полной остановки машины? Сколько метров будет двигаться машина с начала торможения до полной её остановки?

Решение.                             

Мгновенная скорость V(t) машины при торможении равна производной s’(t).

V(t) = S’(t) = (30t – 16t²)՛ = 30 – 32t

 В конце тормозного пути V(t) = 0, поэтому имеем:

30 – 32t = 0, откуда t=  с.

Значит торможение осуществлялось в течении с.

Тормозной путь машины составит:

S () = 30 ·= 16 ()² ≈ 14 (м).

Ответ: t = с.;  S () ≈ 14 м.

3.Тело, масса которого m кг движется прямолинейно по закону x(t) = 3t² + t (в м.). Доказать, что движение тела происходит под действием постоянной силы

Решение.

Ускорение: а(t) = V’(t) = x’’(t)      

V(t) = x’(t) = (3t² + t)׳ = 6t + 1

a(t) = (6t + 1) = 6.

При   данном законе движения тело движется с постоянным  ускорением а(t) = 6 (м/с²). Масса тела m  постоянна, значит по второму закону Ньютона действующая на него сила

F = ma = 6m (Н) также постоянна, что и требовалось доказать.

4.Поворот тела вокруг оси совершается по закону: µ(t) = 2t²-3t+1 радиан. Найти угловую скорость   ω(t) в произвольный момент времени t при t = 2 с.

Решение.

ω(t) = φ՛(t) = (2t²- 3t+1)= 4t- 3 (радиан/с.)

ω(2) = 4·2 – 3 = 5 (радиан/с.)   

Ответ: ω(t)=4t-3 радиан/с., 5 радиан/с.

5.Количество электричества, протекающее через проводник, начиная с момента t=0. задаётся формулой  q = 5t²+4t+2. Найти силу тока в момент времени t=3.

Решение.

I = q^’(t) ; 

I= (5t²+4t+2)’= 10t + 4;

I(t = 3) = 10 * 3 + 4 = 34 (A)

Ответ: 34 A.

ЗАКЛЮЧЕНИЕ

Производная   успешно применяется при  решении различных прикладных задач в науке, технике и жизни.

Наша работа позволяет подтвердить выдвинутую гипотезу, что производная – это инструмент не только исключительно математический, но и позволяющий решать задачи в области физики и техники.

В своей работе мы рассмотрели лишь малую часть применения производной при решении физических задач. Также обширное применение производная находит в физике, химии, биологии, экономике, которая позволяет найти более точный

результат меньшими вычислительными действиями.

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности  решать важные задачи.

Свою работу я хочу закончить  словами Михаила Васильевича Ломоносова: «Слеп физик без математики»

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1.     Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013 г. 189

2.     Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016

3.     Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.

4.     Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.

5.     Колягин Ю.М. Алгебра и начала математического анализа 11 класс, 2010 г.

6.     Рымкевич А.П. Физика. Задачник 10-11 кл.-М.:Дрофа,2006

Использование ресурсов сети Интернет, электронных библиотек:

https://ru.wikipedia.org/wiki/Производная_функции

https://dic.academic.ru/dic.nsf/econ_dict/22069

https://infourok.ru/mini-sbornik-zadach-po-fizike-proizvodnaya-i-integral-pri-reshenii-zadach-255007.html

http://vseuchebniki.net/algebra10/392-uchebnik-algebra-10-11-klass-kolmogorov-2008.html

Скачано с www.znanio.ru