Промежуточная аттестация по алгебре 8

Описание

контрольно-измерительных материалов (КИМ) для проведения в 2023-2024 уч.г. промежуточной аттестации по алгебре

для 8  класса

 

1.      Назначение контрольно-измерительных материалов (КИМ)

Промежуточная аттестация обучающихся — процедура, проводимая с целью определения степени освоения обучающимися содержания учебных предметов/курсов за год в соответствии с образовательным стандартом.

Цель работы – оценить уровень достижения планируемых предметных и метапредметных результатов по алгебре согласно ФГОС и ФОП обучающимися 8 класса.

 

2.      Документы, определяющие содержание КИМ для проведения промежуточной аттестации

 

·         приказ Минобрнауки от 17.12.2010 № 1987 «Об утверждении федеральногогосударственного образовательного стандарта основного общего образования» сизменениями, утвержденными приказом Минобрнауки России от 29 декабря 2014 года№1644, приказом Минобрнауки России от 31 декабря 2015 года № 1577, приказомМинпросвещения России от 11 декабря 2020 года № 712,

·         приказ МинпросвещенияРФ от 18.05.2023 № 370 «Об утверждении федеральной образовательной программы основного общего образования»,

·         ООП ООО МБОУ СОШ № 90 с углубленным изучением предметов ХЭЦ,

·         содержания учебников, включённых в Федеральный перечень.

 

3.      Подходы к отбору содержания, разработке структуры КИМ для проведения промежуточной аттестации

КИМ для проведения промежуточной аттестации основаны на системно-деятельностном, компетентностном и уровневом подходах.

В рамках данной процедуры наряду с предметными результатами освоения основной образовательной программы  основного  общего образования оценивается также достижение метапредметных результатов, в том числе уровень сформированности универсальных учебных познавательных, коммуникативных и регулятивных действий (УУД) и овладения межпредметными понятиями.

Тексты заданий в КИМ в целом соответствуют формулировкам, принятым в учебниках, включенных в Федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования.

 

4.      Форма проведения промежуточной аттестации

 Для промежуточной аттестации используется письменная форма  в виде теста.

 

5.      Структура КИМ для проведения промежуточной аттестации

 

Промежуточная аттестация проходит в письменной форме: тест, составленный в двух вариантах.

Работа содержит 13 заданий, в том числе 11 заданий базового уровня (Часть 1), 2 задания повышенного уровня (Часть 2).    Задания № 3, 6, 7 предполагают   выбор одного правильного ответа из четырех возможных,  задания № 1, 2, 4, 5, 8, 9, 11 – с записью краткого ответа, задание № 10 – на соотнесение, Задания №12 ,13 (повышенный уровень) требуют развернутой записи решения.

 

 

 

 

 

 

 

 

6.      Распределение заданий по проверяемым в КИМ элементам содержания

 

 

№ раздела	Раздел программы	Элементы содержания, проверяемые заданиями КИМ	Код проверяемого элемента содержания
1	Числа и вычисления	Степень с целым показателем и её свойства. Квадратный корень из числа. Понятие об иррациональном числе. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям	1.1
2	Алгебраические выражения	Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей.	2.1
3	Уравнения и неравенства	Квадратное уравнение, формула корней квадратного уравнения.  Решение уравнений, сводящихся к линейным и квадратным. Числовые неравенства и их свойства. Неравенство с одной переменной. Линейные неравенства с одной переменной. Примеры решения систем   уравнений с двумя переменными. Решение текстовых задач алгебраическим способом.	3.1
4	Функции	Понятие функции. Область определения и множество значений функции.  График функции. Чтение свойств функции по её графику.   Функции, описывающие прямую и обратную пропорциональные зависимости, их графики. Функции y = x2, y = x3, y = √x.	4.1
5	Вероятность и статистика	Представление данных в виде таблиц, диаграмм, графиков. Элементарные события случайного опыта. Случайные события. Вероятности событий.	5.1

 

7.      Проверяемые требования к результатам (предметным и метапредметным) обучения

 

№ задания	Код проверяемого элемента содержания	Проверяемые требования к предметным результатам обучения	Проверяемые требования к метапредметным результатам обучения	Уровень сложности
1	2.1	Применять понятие степени с целым показателем, выполнять преобразования выражений, содержащих степени с целым показателем.	Выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях, предлагать критерии для выявления закономерностей и противоречий; делать выводы с использованием законов логики, дедуктивных и индуктивных умозаключений, умозаключений по аналогии; выбирать способ решения учебной задачи;     выбирать, анализировать, систематизировать и интерпретировать информацию различных видов и форм представления; владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи;	базовый
2, 3	1.1	Использовать начальные представления о множестве действительных чисел для сравнения, округления и вычислений, изображать действительные числа точками на координатной прямой. Применять понятие арифметического квадратного корня, находить квадратные корни,  выполнять преобразования выражений, содержащих квадратные корни, используя свойства корней.		базовый
4, 5, 6, 7, 11	3.1	Решать   квадратные уравнения,   системы двух уравнений с двумя переменными. Применять свойства числовых неравенств для сравнения, оценки, решать линейные неравенства с одной переменной и их системы, давать графическую иллюстрацию множества решений неравенства.		базовый
8	2.1	Выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями.		базовый
9	5.1	Находить вероятности случайных событий в опытах, зная вероятности элементарных событий, в том числе в опытах с равновозможными элементарными событиями.		базовый
10	4.1	Понимать и использовать функциональные понятия и язык, определять свойства функции по её графику. Строить графики элементарных функций вида: y = k/x, y = x2, y = x3,y = |x|, y = √x, описывать свойства числовой функции по её графику.		базовый
12	2.1	Выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями.		повышенный
13	3.1	Переходить от словесной формулировки задачи к её алгебраической модели с помощью составления уравнения, интерпретировать в соответствии с контекстом задачи полученный результат.		повышенный

 

 

8.      Система оценивания заданий и работы в целом

 

Максимальная сумма, которую может получить учащийся, правильно выполнивший все задания базового уровня - 11 баллов, повышенного уровня – 4 балла. За верное выполнение каждого задания  первой части работы (№1- №11) выставляется 1 балл. За неверный ответ или его отсутствие выставляется 0 баллов. Задания второй части (№12 - №13) оцениваются от 0 до 2 баллов.  Максимальное количество баллов за всю работу – 15 баллов.

 

 

Критерии оценивания выполнения задания №12		Баллы
Правильно выполнены преобразования, получен верный ответ		2
Решение доведено до конца, но допущена ошибка или описка вычислительного характера, с её учётом дальнейшие шаги выполнены верно		1
Другие случаи, не соответствующие указанным выше критериям		0
Максимальный балл		2
Критерии оценивания выполнения задания №13	Баллы
Правильно составлено уравнение, получен верный ответ	2
Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа	1
Другие случаи, не соответствующие указанным критериям	0
Максимальный балл	2

 

 

 

9.      Шкала перевода баллов (% выполнения работы) в отметку (на основе ОГЭ)

 

 

10.  Время выполнения работы – 40 минут.

 

11.  Описание дополнительных материалов и оборудования, необходимых для проведения работы

 

 

  

  Вариант I

Часть 1

1.      Вычислите .                            Ответ: __________________

2.  Найдите значение выражения:               Ответ: ___________________

3.  Какое из данных чисел принадлежит промежутку [6; 7]?

 1)               2)             3)              4)  

4.  Решите уравнение: х² + 7х – 18 = 0   Ответ: __________________________

5. Решите уравнение   2х² – 18 = 0   Ответ: ______________________________

6.  На координатной прямой отмечены числа a, b и c.

Какая из разностей a − b, a − c, c − b положительна?

 1)  a − b       2)  a − c      3)  c − b        4)  ни одна из них

7. Решите неравенство  20 – 3(х – 5) < 19 – 7х  

и определите, на каком рисунке изображено множество его решений.

1)                                2) 

3)                                4)  

8. Сократите дробь   Ответ: _____________

9.  Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.

Ответ: ______________________________

10.  Установите соответствие между графиками функций и формулами, которые их задают.

ФУНКЦИИ               1)  у = 2х + 4    2) у =            3) у = х²       4) у = 2х

ГРАФИКИ

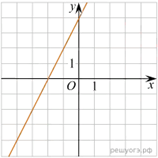
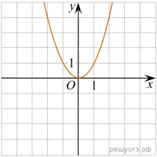
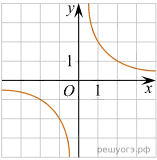
                   А)                                    Б)                                  В)

А	Б	В

Ответ:

 

11. Решите систему уравнений 

Ответ: _____________________

Часть 2

При выполнении заданий Части 2, записывайте полное решение и ответ. Пишите четко и разборчиво.

12. Упростите выражение:

13. Дорога между пунктами A и В состоит из подъема и спуска, а ее длина равна 14 км. Турист прошел путь из А в В за 4 часа, из которых спуск занял 2 часа. С какой скоростью турист шел на спуске, если его скорость на подъеме меньше его скорости на спуске на 3 км/ч?

 

 

Вариант II

Часть 1

1.              Вычислите:  .                 Ответ: ________________

2.  Найдите значение выражения:         Ответ: ____________________

3.  Какое из данных чисел принадлежит промежутку [7; 8]?

 1)              2)             3)               4)  

4.  Решите уравнение: х² + 8х + 12 = 0   Ответ: _____________________________

5. Решите уравнение  5х² + 20х = 0            Ответ: ____________________

6.  Известно, что    Какое из следующих чисел отрицательно?

1)  a – b    2)  a – c     3)  b – c   4)  c - b

7.  Решите неравенство  22 – х > 5 – 4(х – 2)  и определите, на каком рисунке изображено множество его решений.

 

         1)                                                                           2)                               

 

            3)                                                                       4)                                                                                                                                                                                 

                                                                         

8. Сократите дробь:                  Ответ: __________________

 

9.  В фирме такси в данный момент свободно 15 машин: 3 черных, 6 желтых и 6 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.

Ответ: ______________________

 

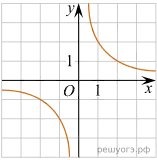
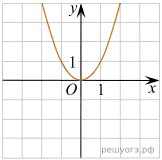
10.  Установите соответствие между графиками функций и формулами, которые их задают.

ФУНКЦИИ

1) у = х²      2) у =               3) у =            4) у =

 

ГРАФИКИ

 

 

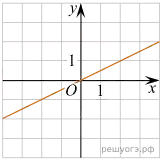
 А)                                                 Б )                                        В)

А	Б	В

Ответ:

 

11. Решите систему уравнений 

Ответ: ___________________

                   

 Часть 2

При выполнении заданий Части 2, записывайте полное решение и ответ. Пишите четко и разборчиво.

12. Упростите выражение:

 13.  Дорога между пунктами A и В состоит из подъема и спуска, а ее длина равна 27 км. Турист прошел путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шел на спуске, если его скорость на подъеме меньше его скорости на спуске на 1 км/ч?

 

 

Ключи

№ задания	1	2	3	4	5	6	7	8	9	10	11	12	13
Вариант 1	16	7	4	- 9; 2	- 3;3	3	1		0,6	132	(2; - 3)	- 3	5
Вариант 2	49	7	4	-6; -2	-4; 0	4	4		0.4	142	(4; 1)	- 4	4

 

 

Скачано с www.znanio.ru