
Графы.
Рассмотрим основное средство создания информационных моделей. К ним можно отнести словесное описание объекта (художественное вещества, статья о нём в словаре). Самым распространённым методом в создании информационной модели является метод описания.. Другим распространённым методом построения и визуализации информационных моделей является графы.
Граф-это отражение некоторого отношения установленного между фиксированными множествами. Из двух множеств в составляющих графа -одно это множество элементов (вершины) а другое множество связей между ними (линии произвольной конфигурации). Граф состоит из множества вершин x и связей между ними U, обозначается G(x,U).
Пример. Известно, что трое учеников учащихся в одном классе помогают друг другу по разным предметам. Изобразим граф отражающий отношение помощи учащихся:

Если порядок соединения не важен, а важно то как они соединены, то такое соединение называют ребром графа А-В. Если важен порядок соединения вершин то такое соединение называют дугой графа и обозначают →.
Граф у которого вершины соединены дугами называют ориентированным. Граф у которого вершины соединены рёбрами называют неориентированным. Граф, вершины которого соединены и дугами и рёбрами называют смешанным.
Две вершины графа называют смежными, если они определяют дугу или ребро. Если вершина являются началом или концом дуги, то говорят, что вершина инцидентна дуге или ребру. Вершины не инцидентные никакому ребру или дуге называют изолированными.
Вершина инцидентная только одному ребру или дуге называется висячей.
Ребро или дуга, граничными вершинами которой является одна и та же вершина называется петлёй.

Виды графов.
Граф без петель и кратных рёбер (дуг) называется обыкновенным (простым, скелетным, графом Берже).
Граф без петель, но с кратными рёбрами (дугами называют мультиграфом).
Граф, соединённый только изолированными вершинами называется пустым или ноль графом.
Обыкновенный граф, в котором любые две вершины соединены ребром называются сльносвязанным или полным графом.
Части графов.
Подграфом С графа G называют граф, образованный из графа G опусканием некоторых вершин и инцидентных им рёбер. Исходный граф по отношению к подграфу является надграфом.
![]()
![]()
1) 2)
Если в результате преобразований число вершин осталось прежним, но были опущены некоторые ребра (дуги)/, то вновь образованный граф считают частичным графом (субграфом) исходного графа.
 Данный
граф является субграфом графа 1, а исходный граф 1 является сверхграфом.
Данный
граф является субграфом графа 1, а исходный граф 1 является сверхграфом.
3)
Маршруты
Маршрут определяется как некоторая последовательность ребер, в котором граничные вершины двух соседних ребер совпадают, например, последовательность ребер 1, 4, 8, 6 – маршрут.
Маршрут, все ребра которого разложены, называется цепью, например, 5, 6, 4, 2.
Замкнутая цепь – это цепь возвращающаяся в ту же вершину, из которой начиналась и она называется циклом, например, 5, 7, 3.
Граф, любая пара вершин которого может быть соединена маршрутом, называется связным, например, 1-3 – связные.
Несвязный граф представляет собой совокупность отдельных частей (подграфов) называемых компонентами связности, например:

4) 5)
Связный граф не создающий циклов, называется деревом, например:
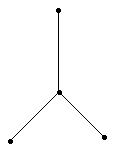
Дерево имеет n вершин, соединенных n-1 ребром.
Несвязный граф, компоненты которого являются деревьями, называется лесом, например:

Способы задания графа
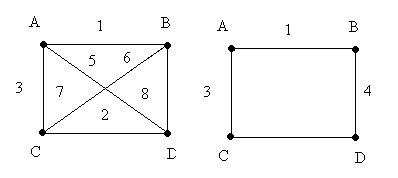
Произвольный граф можно задать совокупностью двух множеств – множество вершин и множество ребер. Вторым способом задания графа является представление его с помощью матрицы.
Матрица связности имеет вид квадратной таблицы, в которой представлены отношения между вершинами, где элемент матрицы – это количество связей (ребер или дуг) для других двух вершин. Если вершины смежные, то ячейка таблицы примет значение 1, если вершины соединены краевыми ребрами, то ячейка таблицы примет значение 2. Так для графа, представленного на рис.1 матрица связности будет иметь вид таблицы.
|
|
A |
B |
C |
D |
E |
|
A |
0 |
1 |
1 |
0 |
1 |
|
B |
1 |
0 |
0 |
1 |
1 |
|
C |
1 |
0 |
0 |
1 |
1 |
|
D |
0 |
1 |
1 |
0 |
1 |
|
E |
1 |
1 |
1 |
1 |
0 |
Из таблицы видно, что наибольшая лок. степень у вершины E: P(E)=4, у всех остальных вершин лок. степень равна 3.
Для того чтобы включенную в структуру модель представить в виде графа не структурную (количественную или текстовую) информацию довольно часто любому ребру (или любой вершине) рассматриваемого графа приписывают некоторый вес.
Граф, ребра (вершина) которого приписаны весу, называется взвешенными. Вес неудобно располагать на чертеже и схеме, поэтому взвешенный граф лучше представить в виде матрицы, такие матрицы называются матрицами весовых соотношений.
Пример: Составить взвешенный граф предложения: “С этого времени Цезарь один управлял всем в государстве по своей воле”.
В этом графе вершинами будут члены предложения, дуги синтетической связи между ними, причем вес приписан и вершинам и дугам, чтобы указать направление дуги в матрице используется знак “+” и “-“ (“+” - главное слово, “-“ -зависимое) связи, которую нужно отразить.
у – управление
с – согласные
к – координация

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.