
Тема. «Пирамида. Усеченная пирамида».
Записать ответы на вопросы.
1. Рисунок любой пирамиды с обозначением всех вершин.
2. Определение пирамиды. Перечислить по рисунку: основание, вершину, боковые ребра, боковые грани, высоту.
3. Определение правильной пирамиды. Записать два обязательных условия, чтобы пирамида была правильной.
4. Что такое апофема правильной пирамиды? Как обозначается?
5. Что такое поверхность фигуры?
6. Что такое объем?
7. Выписать формулу боковой поверхности правильной пирамиды, описать все входящие туда понятия.
8. Выписать формулу полной поверхности правильной пирамиды, описать все входящие туда понятия.
9. Выписать формулу объема пирамиды, описать все входящие туда понятия.
10. Какие две разные высоты входят в формулы боковой поверхности и объема пирамиды?
11. Что такое усеченная пирамида? Сделать рисунок правильной четырехугольной усеченной пирамиды.
12. Выписать формулы для вычисления боковой, полной поверхности и объема усеченной пирамиды.
Решить задачи. ( к каждой задаче должен быть выполнен рисунок, обозначения, краткое условие).
Задача 1. В правильной четырехугольной пирамиде боковое ребро равно 5, сторона основания равна 6. Найти а) боковую поверхность, б) полную поверхность, в) объем пирамиды ( результат умножить на √7).
Задача 2. В правильной треугольной пирамиде боковая поверхность равна 18, апофема равна 4. Найти сторону основания.
Задача 3. Площадь полной поверхности тетраэдра 128. Все ребра увеличили в 3 раза. Какова стала поверхность?
Задача 4. Все ребра октаэдра равны 12√2 . Найти его объем. ( Примечание: радиус описанной окружности около квадрата вычисляется по формуле: R= a √2 / 2 , а – сторона квадрата).
Задача 5. В правильной шестиугольной пирамиде сторона основания равна 18, а боковое ребро равно 41. Найти а) боковую поверхность.
Задача 6. Даны две правильные четырехугольные пирамиды. Объем первой равен 16. У второй высота в 2 раза меньше, чем у первой, а сторона основания в 1,5 раза больше, чем у первой. Чему равен объем второй пирамиды.
Задача 7. В основании пирамиды SABC лежит правильный треугольник ABC со стороной 10. Высота пирамиды обозначена буквой S. Боковое ребро SA перпендикулярно плоскости основания и равно 7√3. Вычислить объем пирамиды.
Задача 8. В основании пирамиды лежит прямоугольник со сторонами 3 и 4. Объем пирамиды равен 32. Вычислить высоту пирамиды.
Задача 9. Объем тетраэдра равен 216. Все ребра уменьшили в 2 раза. Какой будет объем?
Задача 10. В правильной четырехугольной пирамиде полная поверхность равно 40, сторона основания равна 2. Найти апофему пирамиды.
|
|
Пояснения к задачам. Задача № 1. Дано: SB =5, AD=6 Найти а) Sбок.
б) Sпол. в) V
План решения.
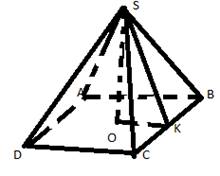 а)
Sбок=
½· Pосн
·hбок, hбок
=SK -
апофема, ее находим по т. Пифагора из
а)
Sбок=
½· Pосн
·hбок, hбок
=SK -
апофема, ее находим по т. Пифагора из
∆ SKB, Pосн. – периметр основания( сумма всех сторон основания- квадрата)
б) Sпир = Sбок + Sосн Sосн – площадь основания, т.е. площадь квадрата.
в) V= 1/ 3· Sосн·h h=SO - высота самой пирамиды, ее находим по т. Пифагора из
∆ SOK , SK – апофема найдена выше, OK =r –радиус вписанной окружности в основание, для квадрата r=a /2 , где а – сторона квадрата.(результат умнож.на √7.)
Задача № 2. В формулу боковой поверхности подставьте заданные величины, найдите оттуда неизвестную величину - периметр основания (сумму всех одинаковых трех сторон). Найдите одну сторону.
Задача № 3 и №9. Это на работу с формулами. Надо посмотреть, в какой степени в формуле находится та величина, которая изменяется (увеличивается или уменьшается), в эту степень возводится величина, на которую происходит изменение. При вычислении площадей эта величина возводится в квадрат, при вычислении объемов в куб. Далее «увеличение» означает умножение на эту величину, «уменьшение» означает деление на это число. Например, поверхность пирамиды была равна 1200. Все ребра уменьшили в 5 раз. а) Какая стала поверхность? б) Какой стал объем?
Решение: а) 5 в квадрате = 25. 1200 / 25 = 48 Ответ: 48.
б) 5 в кубе = 125 1200 /125 = 9,6 Ответ: 9,6.
Задача № 4. Сделайте рисунок. Октаэдр рассматриваем как две одинаковые четырехугольные пирамиды, соединенные своими основаниями. Находим объем одной и умножаем на два. Для нахождения высоты одной пирамиды по т. Пифагора нужен R - радиус описанной окружности около квадрата в основании пирамиды R= a·√2 / 2. Ребро октаэдра – гипотенуза, R – катет, находим высоту. По формуле вычисляем объем
( Sосн – площадь квадрата). Не забудьте удвоить результат!!!
Задача № 5. Сделайте рисунок. Найдите апофему по т.Пифагора как в зад. №1, зная гипотенузу-это боковое ребро, оно равно 41 и половину стороны основания 18/2 =9. Найдите периметр основания (там правильный шестиугольник).Подставьте найденные величины в формулу Sбок.
Задача № 6. В этом образце условие другое, но подобное, как№6 . Даны две правильные треугольные пирамиды (какие пирамиды роли не играет). Объем первой равен 600. У второй высота в 4 раза меньше, а сторона основания в 3 раза больше. Чему равен объем второй. Решение. В формулу объема пирамиды высота входит в первой степени, а в площади основания сторона входит всегда в квадрате. Поэтому, 600 делим на 4 (т.к. в 4 раза меньше высота), а умножаем на 3 в квадрате) (600 / 4)·9=2025.
Задача № 7. Сделать рисунок. Выписать формулу для объема пирамиды. Площадь основания в этой формуле - это площадь правильного треугольника: S = сторона треугольника в квадрате умножить на √3 все разделить на 4. Боковое ребро в этой задаче – это высота, т.к. по условию ребро SA перпендикулярно основанию. Подставить величины в формулу.
Задача № 8. Сделать рисунок как в зад.№1. Выписать формулу объема пирамиды.
Вычислить площадь основания, как площадь прямоугольника. Подставить в формулу объема: в левую часть формулы величину объема, заданную по условию, в правую часть вычисленную площадь основания, выразить оттуда и вычислить высоту.
Задача № 10. Выписать формулу полной поверхности пирамиды. S пол.=Sбок + Sосн = ½· Pосн ·hбок + Sквадрата. Зная сторону основания а=2, вычислить Pосн. ( периметр, как сумму всех четырех сторон) и площадь квадрата.
Подставить в левую часть формулы известную Sпол =40, в правую часть -вычисленные периметр и площадь квадрата, найти единственную неизвестную величину hбок - апофему.
Самостоятельная работа.
|
|
Вариант 1 |
|
Вариант 2 |
|
1 |
В правильной треугольной пирамиде SABC медианы треугольника АВС пересекаются в точке О. Площадь треугольника АВС равна 2, объем пирамиды равен 6. Найти SO. |
1 |
В правильной треугольной пирамиде SABC медианы треугольника АВС пересекаются в точке О. Площадь треугольника АВС равна 9, объем пирамиды равен 6. Найти SO. |
|
2 |
В правильной треугольной пирамиде SABC L – середина ребра АС, сторона ВС равна 6, отрезок SL равен 5. Найти боковую поверхность пирамиды. |
2 |
В правильной треугольной пирамиде SABC L – середина ребра АС, сторона ВС равна 12, отрезок SL равен 10. Найти боковую поверхность пирамиды. |
|
3 |
В правильной четырехугольной пирамиде SABCD точка О – центр основания ABCD. Ребро SD равно 10, отрезок SO равен 6. Найти АС. |
3 |
В правильной четырехугольной пирамиде SABCD точка О – центр основания ABCD. Ребро SD равно 13, отрезок SO равен 5. Найти АС. |
|
4 |
В правильной четырехугольной пирамиде сторона основания равна 8, а длина бокового ребра равна 9. Найти высоту пирамиды. |
4 |
В правильной треугольной пирамиде сторона основания равна 6, а длина бокового ребра равна 4. Найти высоту пирамиды. |
|
5 |
Высота правильной четырехугольной пирамиды равна 10, а сторона основания равна 15. Найти длину апофемы этой пирамиды. |
5 |
Высота правильной треугольной пирамиды равна 2, а сторона основания равна 12. Найти длину апофемы этой пирамиды. |
|
6 |
Радиус окружности, вписанной в основание правильной четырехугольной пирамиды равен 4√5,а длина бокового ребра пирамиды равна 14. Найти высоту пирамиды. |
6 |
Радиус окружности, вписанной в основание правильной треугольной пирамиды равен 12,а длина бокового ребра пирамиды равна 26. Найти высоту пирамиды. |
|
7 |
Плоскость, параллельная плоскости основания правильной четырехугольной пирамиды, делит высоту пирамиды в отношении 1:2, считая от вершины. Апофема полученной усеченной пирамиды равна 4дм, а площадь ее полной поверхности равна 186 дм2. Найдите объем усеченной пирамиды. |
7 |
Плоскость, параллельная плоскости основания правильной четырехугольной пирамиды, делит высоту пирамиды в отношении 1:4, считая от вершины. Апофема полученной усеченной пирамиды равна 16 дм, а площадь ее полной поверхности равна 744 дм2. Найдите объем усеченной пирамиды. |
|
8 |
Стороны основания правильной треугольной усеченной пирамиды 40 см и 20 см, а боковое ребро равно 20 см. Найдите объем и боковую поверхность пирамиды. |
8 |
Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 см и 3 см. Одно из боковых ребер перпендикулярно к плоскости основания и равно 1 см. Найдите площадь боковой поверхности и объем пирамиды. |
|
9 |
В правильной усеченной четырехугольной пирамиде стороны основания 6 см и 4 см, а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна 15 см2. Найдите объем усеченной пирамиды. |
9 |
В правильной усеченной четырехугольной пирамиде радиусы вписанных окружностей в основания 12 см и 8 см, а боковое ребро 5 см. Найдите объем усеченной пирамиды. |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.