Прямоугольник, ромб , квадрат(основные свойства)

Прямоугольник – это параллелограмм, у которого все углы прямые.  Данное определение можно скорректировать, заменив слово «параллелограмм» на «четырёхугольник», прямоугольник – это четырёхугольник, у которого все углы прямые.  Он обладает следующим свойством – диагонали прямоугольника равны. Тогда верно и обратное утверждение, которое является признаком прямоугольника: если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. Напомним, что площадью прямоугольника является произведение его длины на ширину.

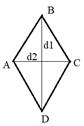Ромбом называется параллелограмм, у которого все стороны равны. Ромб обладает следующими характерными ему свойствами: диагонали ромба взаимно перпендикулярны и являются биссектрисами углов. Площадь ромба вычислить несколькими способами.

I способ

Площадь ромба равна полупроизведению диагоналей.

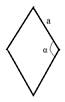II способ

Площадь ромба равна произведению квадрата стороны на синус угла.

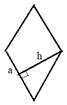III способ

Площадь ромба равна произведению высоты на сторону.

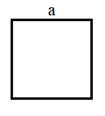И, наконец, квадрат – это прямоугольник, у которого все стороны равны. Основными свойствами являются следующие: все углы квадрата прямые; диагонали равны, взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами углов. Площадь квадрата можно вычислить, как квадрат стороны.