РАБОТА С ТЕКСТОМ 

НА УРОКАХ МАТЕМАТИКИ

ПРОВЕРКА СВЯЗИ

+ +         видно и слышно

+ -          только слышно или только видно

- -           не видно и не слышно

СПИКЕР ВЕБИНАРА

Жогликова Наталья

Ивановна 

учитель математики, информатики и ВТ в МАОУ Плешковская СОШ

Квалификационный разряд – высшая категория (21.03.17, Приказ №34-к).

Стаж работы – 31 год.

ОБЩИЕ СВЕДЕНИЯ ОБ УЧИТЕЛЕ

Дата рождения – 23 августа 1970 года.

Образование – Тобольский педагогический институт им. Д. И. Менделеева.

«Мы слишком часто даем детям ответы, которые надо выучить, а не ставим  перед ними проблемы, 

 которые надо решить».

Роджер Левин 

ПЛАН ВЕБИНАРА

1.   Ключевые направления формирования умений работы с текстом на уроках.

2.   Этапы работы с текстом на уроках математики.

3.   Примеры использования умений с уроков.

4.   Памятки работы с текстом на уроках математики.

5.Упражнения для совершенствования навыков чтения. 

ПРОБЛЕМА:

Как научить школьников самостоятельно работать с текстом учебника?

РЕШЕНИЕ ПРОБЛЕМЫ –

организация систематической работы с учебником математики на каждом уроке и дома по трем этапам: 

•   до чтения;  • во время чтения;

•   после чтения. 

КЛЮЧЕВЫЕ НАПРАВЛЕНИЯ формирования умений работы с текстом

V – VI классы

•   выделение главного в тексте;

•   составление примеров, аналогичных приведенным в тексте;

•   умение найти в тексте ответ на поставленный вопрос;

•   грамотно пересказать прочитанный текст.

VII – VIII классы

•    умение составить план прочитанного;

•    воспроизводить текст по предложенному плану; • умение пользоваться образцами решения задач;

•    запоминание определений, формул, теорем.

IX – XI классы

•    работа с иллюстрациями (рисунками, чертежами, диаграммами);

•    использование новой теории в различных учебных и жизненных ситуациях;

•    подтверждение научных фактов;

•    конспектирование новой темы.

1 ЭТАП – РАБОТА ДО ЧТЕНИЯ

•   игра «Попробуй найти!»; 

•   прием «Банк идей (гипотез)»; 

•   прием «Верные или неверные утверждения» или «Верите ли Вы?».

ПРИМЕР

В начале изучения темы «Углы» в 5 классе можно предложить учащимся поиграть в игру «Верю – не верю»: 

•    тупой угол – это угол, который нарисован тупым карандашом;

•    угол – это геометрическая фигура;

•    угол состоит из двух пресекающихся прямых;

•    бывают углы остроумные и тупые;

•    угол состоит из двух лучей, выходящих из одной точки;

•    равные углы – это те, у которых равны стороны;

•    биссектриса – это такой угол, у которого три стороны;

•    бывает угол прямой;

•    угол может быть тощим;

•    острый угол – это угол, который меньше прямого.

Жогликова Наталья Ивановна, учитель математики

2 ЭТАП – РАБОТА С ТЕКСТОМ УЧЕБНИКА НЕПОСРЕДСТВЕННО

Основными   целями       чтения    параграфа учебника могут быть: 

•    знакомство с информацией, заложенной в выбранном фрагменте текста;

•    понимание информации;

•    запоминание; 

•    использование информации в различных учебных и жизненных ситуациях; 

•    подтверждение изученного или того, что знали ранее; 

•    отыскание примеров; 

•    подтверждение научных фактов;

•    работа   с     иллюстрациями (рисунками, чертежами, диаграммами).

10 КЛАСС – ГЕОМЕТРИЯ

К п. 146. Свойства перпендикулярных прямой и плоскости.

1. Заполни пропуски.

Теорема _________. Если плоскость _________________ одной ____ двух параллельных ____________, _____ она перендику______ и  ________ой.

Доказательство.

Пусть а1 и _ – две параллельные прямые и __ – плоскость, _________ прямой а1 (рис. __). __________, что эта плоскость перпендикулярна и ________ а2.

Проведем _________ точку А2 пересечения прямой а2  с плоскостью  произвольную __________ х2 в плоскости ___. Проведем в ________  через точку А_ пересечения прямой а1 с плоскостью прямую _______  параллельную прямой х2.    Так как прямая а1 _ _ _ _ _ _ _ _ _ _ _ _ _ плоскости, ___ прямые

а1 и х1 _________________. А по ______17.1. параллельные им пересекающи__ прямые а2 и х2 тоже перпендикулярны. 

Таким ______, прямая а2 перпендикулярна любой прямой х2 ___плоскос__ . А это _____, что прямая _____ перпен___________ плоскости .

Теорема доказана.

2.Постройте в пространстве три проходящих через одну точку взаимно перпендикулярных прямых.

3. Укажи верно ли утверждение, если да, то напиши слово да, если нет, то исправь ошибки в тех местах, где ты считаешь неверно: 

а) прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она параллельна любой прямой, которая не лежит в данной плоскости и проходит через точку пересечения; 

б) две прямые называются перпендикулярными,  если они не пересекаются; 

в) если прямая, пересекающая  плоскость,  перпендикулярна двум прямым в этой  плоскости, то она перпендикулярна  плоскости.

Методический прием «Инсерт»

Умножение натуральных чисел 

и его свойства

«Определите, какие из равенств верные?»

5∙a = 5a

5+b = 5b

(x+4)∙(y-5) = (x+4)(y-5)

6∙8∙n = 48n x∙(2+c) = x(2+c)

7∙2+k = 14k

(ab)∙c = abc

Важным из способов записи прочитанного,  особенно для старших классов,  является конспектирование.

СОСТАВЛЕНИЕ ТЕЗИСОВ

Можно сравнить план и тезисы на примере одного и того же текста из учебника математики для 5 класса «Угол».

План.

1.   Понятие угла.

2.   Равные углы.

3.   Развёрнутый угол.

4.   Прямой угол.

Тезисы.

1.   Углом называют фигуру, образованную двумя лучами, выходящими из одной точки. Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят,- вершиной угла. 

2.   Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.

3.   Два дополнительных друг другу луча образуют развёрнутый угол. Стороны этого угла вместе образуют прямую линию, на которой лежит вершина развёрнутого угла.

4.   Прямым углом называют половину развёрнутого угла.       

3 ЭТАП – РАБОТА ПОСЛЕ ЧТЕНИЯ

•   «Дерево знаний»;

•   игра «Угадай-ка!».

ЧТО ЗНАЧИТ: РАЗДЕЛИТЬ С ОСТАТКОМ?

Чтобы ответить на этот вопрос, решим задачу:

В гости к бабушке пришли 4 внука. Бабушка решила угостить внуков конфетами. В вазочке было 23 конфеты. Сколько конфет достанется каждому внуку, если бабушка предложит поделить конфеты поровну?

Рассмотрите вопросы и определите, сколько раз ученику приходится перечитать задачу.

Учитель: Сколько конфет у бабушки?

Ученик: У бабушки 23 конфеты.  Учитель: Сколько внуков пришло в гости к бабушке?

Ученик: В гости пришли 4 внука.

Учитель: Что необходимо сделать по условию задачи?

Ученик: Конфеты нужно поделить поровну, надо разделить 23 на 4. 

Ученик: 23 делится на 4 с остатком: в частном получится 5, а в остатке 3.

Учитель: Сколько же конфет достанется каждому внуку?

Ученик: Каждому внуку достанется по 5 конфет и в вазочке останется 3 конфеты.

5 КЛАСС – ДЕЛЕНИЕ И ДРОБИ

Определение темы урока: найдите значение выражения, используя свойство деления:

(38 + 95) : 19;   

296 : 8 + 504 : 8.

КАРТОЧКИ К УРОКУ

1) Допишите правило:

-   Черта дроби – это … .

-   Если разделить нацело нельзя, то … .

2)    Запишите в виде дроби частное:

а) 4:7;                

б)  8:11.

3)    Запишите дробь в виде частного: 

а) ;

б) .  

СОВЕРШЕНСТВОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ

Составьте из букв слово:

а о и л п и а м д

УЧАСТНИКИ ОЛИМПИАДЫ

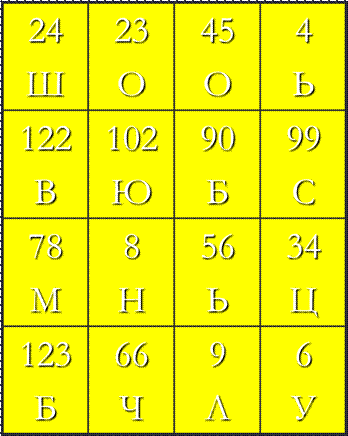1) Сумма чисел 54 и 36. 2) Уменьшаемое 45, вычитаемое

22.  Найдите разность. 3) 2х=18. Найдите корень уравнения.

4)        5х=16+х. Найдите корень  уравнения.

5)        Первое слагаемое – 16, второе  Слагаемое – 7. Найдите сумму.

6)        От точки Е(10) влево отступили 4 единичных отрезка. Чему равна координата новой точки?

8)   56 : 7.

9)   87 – (–35).

ЧТО У ВАС ПОЛУЧИЛОСЬ?

•    Б 

•    О

•    Л 

•    Ь

•    Ш 

•    У   

•    Н 

•    О

•    В

АЛЕКСАНДР БОЛЬШУНОВ

_____февраля 2018 года в

Пхенчхане Александр Большунов завоевал бронзу на Олимпиаде-2018. 

21-летний атлет выступил в финале мужского спринта в классическом стиле.

13*2*5:10

УРОК ГЕОМЕТРИИ – 8 КЛАСС

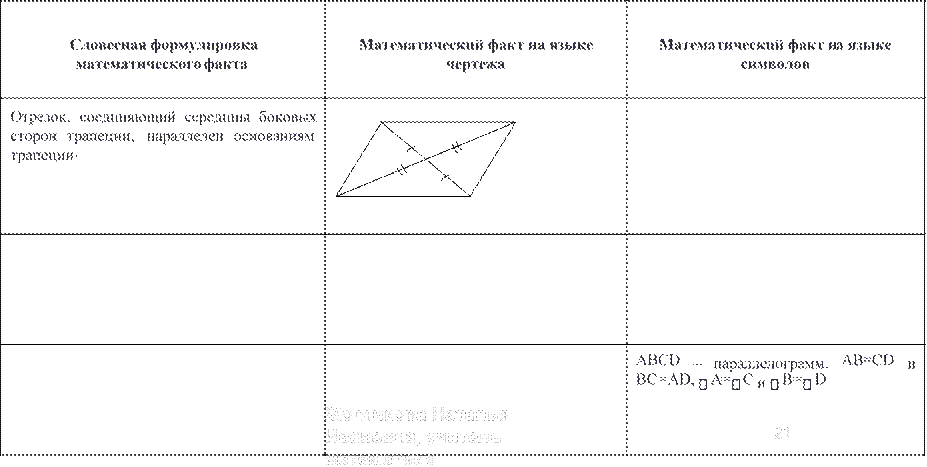
Средняя линя трапеции. Решение задач.

Задачи на этапе урока: «Актуализация опорных знаний»

По теме: «Средняя линия треугольника»

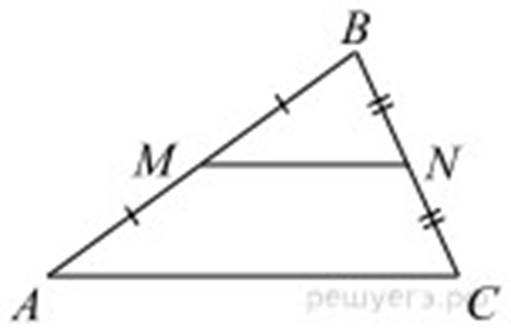Точки М и N являются серединами сторон  AB и BC треугольника ABC, сторона AB  равна – 66, сторона BC равна – 37, сторона  AC равна – 100. Найдите MN. 

ПРОВЕРКА САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Какие из следующих утверждений верны?

1.         Четырехугольником называется фигура, которая состоит из трех точек и четырех последовательно соединяющих эти точки отрезков. При этом точки не должны лежать на одной прямой, а отрезки не должны пересекаться;

2.         Прямоугольник—это параллелограмм, у которого все углы прямые;

3.         Средней линией треугольника называется отрезок, который соединяет середины двух  его сторон;

4.         Средняя линия треугольника, соединяющая середины двух боковых сторон, перпендикулярна третьей стороне и равна её половине.

Ответ: ___________________________ 

СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ. РЕШЕНИЕ ЗАДАЧ

Цели: 

–          закрепить способы решения задач с использованием теоремы Фалеса, средней линии треугольника и трапеции;

–          содействовать рациональной организации труда учащихся;

–          продолжить совершенствовать вычислительные навыки.

Решение задач. 1) Повторение: термин – трапеция, теорема о средней линии трапеции. Рассмотрение доказательства данной теоремы.

Теорема 6.8. Средняя линия трапеции  параллельна основаниям и равна их полусумме. 

Доказательство: пусть ABCD – данная трапеция. 

1.  Выполним дополнительное построение: продолжим сторону АД. Из точки В проведем отрезок ВЕ. 

2.  ΔРВС=ΔРЕД (почему?) (стр.92 учебного пособия, в доказательстве 4 строчка)

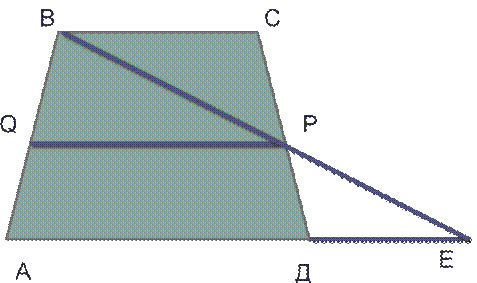3.Из равенства треугольников следует равенство сторон: РВ=РЕ, ВС=ЕД.

4.Зачит, PQ средняя линия трапеции, является средней линией треугольника.

5. По свойству средней линии треугольника…(учебник)

МИНУТКА ОТДЫХА

В автобусе ехало 50 человек. 

На остановке 7 человек вошли, а 3 – вышли;  на следующей вошел – 1, а вышли – 4;  на следующей 5 –  вошли,4 – вышли;  на следующей вышли – 15, вошли – 2. 

Сколько остановок сделал автобус?

РЕШЕНИЕ ЗАДАЧ ПО ЧЕРТЕЖАМ

Задание 1.

Какие четырехугольники являются трапециями?

Назовите их основания и боковые стороны.

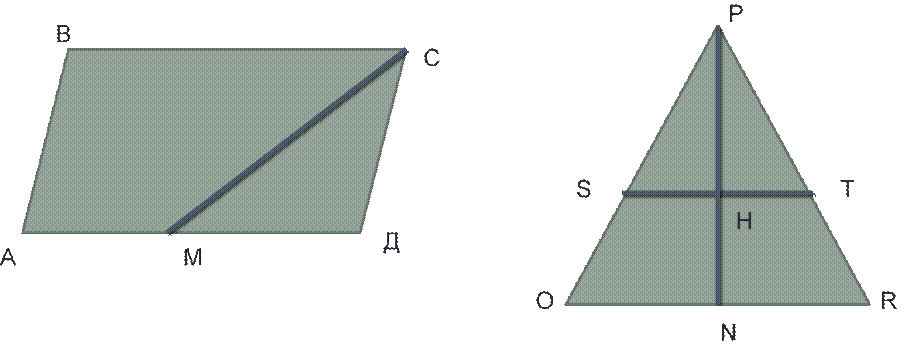
Задание 2.

В трапеции МНРК проведен отрезок РЕ, параллельный МН. Определите вид четырехугольника МНРЕ.

Выполнить чертеж и дать ответ по заданию.

Задание 3.

Сколько средних линий можно построить в данной трапеции?

Постройте чертеж для данного задания.

РЕШЕНИЕ ЗАДАЧИ ИЗ ОГЭ О СРЕДНЕЙ ЛИНИИ ТРАПЕЦИИ

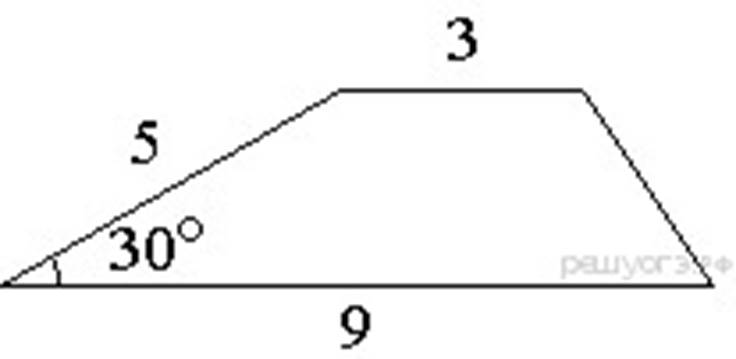
На клетчатой бумаге с размером клетки 1х1 изображена трапеция АВСД. Найдите длину ее средней линии.

САМОСТОЯТЕЛЬНАЯ РАБОТА

ФИГУРЫ НА КВАДРАТНОЙ РЕШЕТКЕ (№ 348638; № 349153)

ИТОГ УРОКА

•    О чем мы говорили на уроке?

•    Дайте определение средней линии трапеции.

•    Объясните, как можно найти среднюю линию трапеции.

•    Что помогает еще найти средняя линия трапеции?

ДОМАШНЕЕ ЗАДАНИЕ

1.         П. 59, термины, понятия, вопросы 17-19,  задачи в тетради, решить №61.

2.         Решить ОГЭ – 2 задания о средней линии трапеции прорешать и записать в тетрадь.

ПАМЯТКА РАБОТЫ С ПАРАГРАФОМ УЧЕБНИКА МАТЕМАТИКИ ДЛЯ УЧЕНИКОВ 5-6 КЛАССОВ

•     Прочитай заголовок и попытайся ответить на вопрос: «О чем будет говориться в этом параграфе?».

•     Просмотри текст параграфа, обращая внимание на иллюстрации, правила, примеры.

•     Почитай текст. Установи связь текста и иллюстраций, правил, примеров рассмотренных ранее.

•     Как выделено главное в тексте (правила, алгоритмы выполнения действий и т.п.).

•     Приведи свои примеры к тексту.

•     Раздели текст на смысловые части. Сколько их  получилось?

•     Озаглавь части текста и составь план.

•     Выполни письменное задание.

•     Повтори прочитанное по плану, затем без него. 

•     Проговори несколько раз правила. Выучи наизусть.

ПАМЯТКА РАБОТЫ С ПАРАГРАФОМ УЧЕБНИКА МАТЕМАТИКИ ДЛЯ УЧЕНИКОВ 7-9 КЛАССОВ

•     Прочитайте заголовок параграфа. Что вы уже знаете об этом? Что вы говорили в классе об этом?

•     Прочитайте текст параграфа.

•     Выучите формулировки теорем, определения, правила, алгоритмы решения заданий.

•     Установите связь между иллюстрациями, рисунками, чертежами и текстом.

•     Разделите текст на части, озаглавьте их, запишите план в тетрадь.

•     Выполните письменное домашнее задание.

•     Перескажите теоретические сведения, прочитанные из параграфа, согласно вашему плану.

•     Приведите собственные примеры в доказательство прочитанного.

ПАМЯТКА РАБОТЫ С ПАРАГРАФОМ УЧЕБНИКА МАТЕМАТИКИ ДЛЯ УЧЕНИКОВ 10-11 КЛАССОВ

•     Прочитайте заголовок параграфа. Что вы записали в классе по этому вопросу?

•     Просмотрите текст параграфа. Рассмотрите иллюстрации, попробуйте их объяснить.

•     Прочитайте текст параграфа. Заучите определения, формулировки, правила. Восстановите «пробелы текста».

•     Рассмотрите алгоритмы решения заданий.

•     Выполните письменное домашнее задание.

•     Перескажите прочитанный материал.

•     Составьте схему прочитанного материала или табличный вариант.

РАБОТА ПО ЗАДАНИЯМ ЕГЭ

Телефонная компания предоставляет на выбор три тарифных плана. Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 700 минут в месяц. 

Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 700 минут? 

Ответ дайте в рублях.

РАБОТА ПО ЗАДАНИЯМ ЕГЭ

РАБОТА ПО ЗАДАНИЯМ ЕГЭ

Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Валентина Петровна получила 10440 рублей.

Сколько рублей составляет заработная плата Валентины  Петровны?

РАБОТА ПО ЗАДАНИЯМ ЕГЭ

Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой: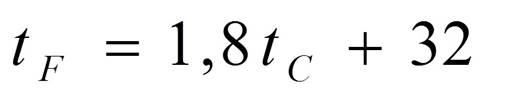     

–         температура в градусах по шкале Цельсия.

–         температура в градусах по шкале Фаренгейта.

Скольким градусам по шкале Фаренгейта соответствует 23 градуса   по шкале Цельсия?

РАБОТА ПО ЗАДАНИЯМ ЕГЭ

На день рождения полагается дарить букет из нечетного числа цветов. Роза стоит 50 рублей за штуку. У Сережи есть 650 рублей. 

Из какого наибольшего числа роз он сможет купить букет

Марине на день рождения?

ЧТЕНИЯ

1. Упражнения, направленные на развитие четкости произношения – звуковая разминка:

1). Артикуляция. Артикуляция гласных, согласных, их сочетаний. Пропевание гласных:

АОУЫЭ,  ЯЁЮИЕ,  АЯОЁУЮЭЕЫИ

АО, УА, АЫ, ИО, ЭА, АУ

З-С-Ж, Ш-Ж-С, С-Ч-Щ

Б-В-Г-Д-Ж-З, П-Ф-К-Т-Ш-С

Ба-бя   бо-бё   бу-бю   бэ-бе   бы-би

За-зя    зо-зё    зу-зю    зэ-зе    зы-зи

ЧТЕНИЯ

2)            Слова, трудные для произношения (портфель,

иллюминация).

3)            Скороговорки. Чтение и четкое проговаривание скороговорок. Чтение скороговорок в темпе:

Утром, присев на пригорке, учат сороки скороговорки.

От топота копыт пыль по полю летит.

Шел Егор через двор с топором чинить забор. Проворонила ворона вороненка.

Эти упражнения развивают подвижность речевого аппарата.

ЧТЕНИЯ

2.               Упражнения, вырабатывающие внимание к слову и его частям и являющиеся предпосылкой правильного чтения.

3.               Упражнения, развивающие оперативное поле чтения и память:

Игра «Фотоглаз»

Сфотографировать (запомнить) несколько слов, написанных взрослым, и ответить на вопрос – есть ли слово, которое произносит взрослый, в перечне или нет? 

Или учащийся вместе с учителем читает несколько слов, а затем учитель спрашивает, какое слово находится на 1 месте.

Цель этого вида работы: развитие поля чтения, зрительного восприятия слов. Влияет прием и на совершенствование устойчивости внимания, оперативной памяти.

ЧТЕНИЯ

4. Упражнения, развивающие гибкость и скорость чтения вслух и про себя, умение угадывать последующий текст:

«Молния»

Упражнение заключается в чередовании чтения в комфортном режиме с чтением на максимально доступной каждому скорости чтения про себя с чтением вслух. 

Переход на чтение в максимально ускоренном режиме происходит по команде «Молния» и длится с 20 секунд (в начале) до 2-х минут.  Упражнение используется для повышения верхней границы индивидуального диапазона скорости.

«Буксир»

Взрослый читает текст, варьируя скорость чтения в пределах 80 – 160 слов в минуту. Дети читают тот же текст про себя, стараясь успевать за взрослым. Проверка осуществляется        путем внезапной остановки на каком-либо слове. Дети должны остановиться на этом месте, показать слово.

ЧТЕНИЯ

«Чтение за взрослым (вслух)» Это упражнение вырабатывает скорость произношения слов.

«Сравнение скорости чтения известного текста  и незнакомого» Это упражнение активизирует деятельность учащихся, т.к. они видят свой рост и убеждаются в том, что труд приносит успехи.

«За одну минуту найти в тексте слова на какую-либо букву»

«Кто быстрее?» Требуется найти в тексте предложение, которое прочитал учитель. По команде «Начали» ученик «скользит по тексту» в поисках данного предложения.

«Разведка»

Это чтение используется в целях обучения детей вертикальному чтению. Оно заключается в том, что дети с максимальной для них скоростью просматривают текст и находят ответы на вопросы, поставленные учителем перед чтением. Таким образом, дети не только учатся вертикальному чтению, но и умению ориентироваться в тексте, находить главное.

«Жужжащие чтение»

«Читать пред сном»

Если ребенок не любит читать, то необходим режим щадящего чтения. 

Важна не длительность, а частота тренировочных упражнений. 

НАПРАВЛЕНИЯ, НАД КОТОРЫМИ НЕОБХОДИМО РАБОТАТЬ

•    Повышение скорости и одновременно качества чтения.

•    Развитие речи учащихся (синтаксический уровень).

•    Расширение, углубление, упорядочение читательского кругозора.

•    Привлечение родителей для привития любви к чтению.

СПАСИБО ЗА ВНИМАНИЕ!