Разбор заданий ОГЭ информатика 1-6 вопрос

Задание ОГЭ №1 "Количественные параметры информационных объектов"

Теоретический материал.

Что нужно знать:

Алфавит — это набор знаков, который используется в языке.

Мощность алфавита — это количество знаков в алфавите.

Сообщение — это любая последовательность символов некоторого алфавита.

Если алфавит имеет мощность M, то количество всех возможных «слов» (символьных цепочек) длиной L (без учета смысла) равно N = M^L; для двоичного кодирования (мощность алфавита M  – 2 символа) получаем известную формулу: N = 2^L.

1 байт = 8 бит

1 Кбайт (килобайт) = 1024 байта

1 Мбайт (мегабайт) = 1024 Кбайт

1 Гбайт (гигабайт) = 1024 Мбайт

1 Тбайт (терабайт) = 1024 Гбайт

1 байт = 2³ бит

1 Кбайт = 2¹⁰ байта = 2¹⁰ ⋅ 2³ бит = 2¹³ бит

1 Мбайт = 2¹⁰ Кбайт = 2¹⁰ ⋅ 2¹³  бит = 2²³ бит

 Таблица степеней двойки, она же показывает, сколько вариантов N можно закодировать с помощью K  бит:

K, бит	1	2	3	4	5	6	7	8	9	10
Q, вариантов	2	4	8	16	32	64	128	256	512	1024

 

При измерении количества информации принимается, что в одном байте 8 бит, а в одном килобайте (1 Кбайт) – 1024 байта, в мегабайте (1 Мбайт) – 1024 Кбайта

Чтобы найти информационный объем сообщения (текста) I, нужно умножить количество символов (отсчетов) L на число бит на символ (отсчет) K:  

I = L * K

Две строчки текста не могут занимать 100 Кбайт в памяти

Примеры решения задач:

Задание 1

В одной из кодировок Unicode каждый символ кодируется 16 битами. Петя написал текст (в нём нет лишних пробелов):

«Ель, кедр, сосна, кипарис, лиственница, можжевельник  — хвойные растения».

Ученик вычеркнул из списка название одного из растений. Заодно он вычеркнул ставшие лишними запятые и пробелы  — два пробела не должны идти подряд.

При этом размер нового предложения в данной кодировке оказался на 26 байт меньше, чем размер исходного предложения. Напишите в ответе вычеркнутое название хвойного растения.

Решение.

Поскольку один символ кодируется двумя байтами, из текста удалили 13 символов. Заметим, что лишние запятая и пробел занимают четыре байта. Значит, название растения, которое удалили из списка, должно состоять из 11 букв, поскольку (26 − 4): 2 = 11 символов. Из всего списка только одно название растения состоит из 11 букв — лиственница.

Ответ: лиственница

Задание 2

Рассказ, набранный на компьютере, содержит 2 страницы, на каждой странице 32 строки, в каждой строке 64 символа. Определите информационный объём рассказа в Кбайтах в одной из кодировок Unicode, в которой каждый символ кодируется 16 бит.

 Решение.

Найдем количество символов в рассказе:

2 · 32 · 64 = 2¹ · 2⁵ · 2⁶ = 2¹².

Один символ кодируется двумя байтами, 2¹⁰ байт составляют 1 Кбайт, поэтому информационный объем статьи составляет

2 · 22 ·  2¹⁰ байт = 8 Кбайт.

Ответ: 8.

Задание 3.

В одной из кодировок Unicode каждый символ кодируется 16 битами. Определите размер в байтах следующего предложения в данной кодировке: Я к вам пишу — чего же боле? Что я могу ещё сказать?

Решение.

Каждый символ кодируется 16 битами или двумя байтами. Всего символов в данном предложении — 52, включая пробелы. Следовательно, ответ 104 байт.

 Ответ: 104.

 Примечание.

37 символов русского алфавита + 3 специальных символа + 12 пробелов (длинное тире обособляется пробелом с двух сторон) = 52 символа.

Задание 4.

В одной из кодировок каждый символ кодируется 8 битами. Вова написал текст (в нём нет лишних пробелов):

«Фиалка, лютик, роза, гвоздика, мак, хризантема,
   гладиолус – это цветы».

Затем он добавил в список название ещё одного растения. Заодно он добавил необходимые запятые и пробелы. При этом размер нового предложения в данной кодировке оказался на 10 байт больше, чем размер исходного предложения. Напишите в ответе длину добавленного названия растения в символах.

Решение.

Один символ кодируется одним байтом, значит в текст добавили 10 символов. Заметим, что лишние запятая и пробел занимают два байта. Значит, название растения, которое добавили в список, должно состоять из 8 букв, поскольку 10 - 2 = 8 символов.

Ответ: 8

Задание ОГЭ №2 "Кодирование информации"

Теоретический материал:

Различают равномерное и неравномерное кодирование. При равномерном кодировании каждый символ кодируется одинаковым количеством разрядов. Для декодирования такой последовательности достаточно разделить её на группы, соответствующие количеству разрядов.

При неравномерном кодировании различают:

1) Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова (условие Фано). Сообщения декодируются однозначно слева направо.

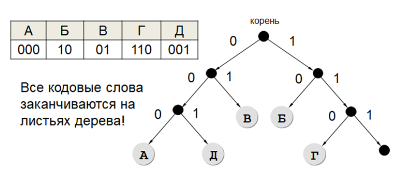
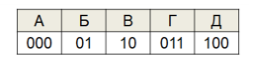
2) Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с окончанием другого кодового слова. Сообщения декодируются однозначно (с конца!).

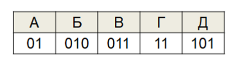
3) Неоднозначное декодирование - это код, в котором не выполняется ни прямое, ни обратное условие Фано

Примеры решения задач.

1. От разведчика было получено сообщение:

  1110011001100101

В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы А, Б, К, Л, О, С; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль. 

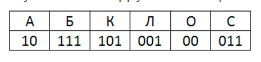
В данном задании выполняется обратное условие Фано. Поэтому можно однозначно декодировать последовательность с конца.

111_001_10 _011_00_101

Получается "бласок"

Ответ: бласок

 2. От разведчика было получено сообщение:

  100111000110111001

В этом сообщении зашифрован пароль – последовательность русских букв. В пароле использовались только буквы А, Б, К, Л, О, С; каждая буква кодировалась двоичным словом по таблице, показанной на рисунке. Расшифруйте сообщение. Запишите в ответе пароль.

 

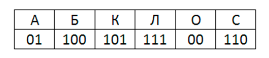
В данном задании выполняется прямое условие Фано. Поэтому можно однозначно декодировать последовательность с начала строки.

100_111_00_01_101_110_01

Получается "блоакса".

Ответ: блоакса

3. Валя шифрует русские слова (последовательности букв), записывая вместо каждой буквы её код:

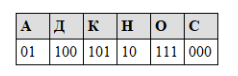
Некоторые цепочки можно расшифровать не одним способом. Например, 00010101 может означать не только СКА, но и СНК. Даны три кодовые цепочки:

 1010110

11110001

100000101

Найдите среди них ту, которая имеет только одну расшифровку, и запишите в ответе расшифрованное слово.

Первая строка может быть расшифрована: КАД, НКН – не подходит.

Вторая строка может быть расшифрована: ОДА – других вариантов нет.

Третья строка может быть расшифрована: ДСК, НСАА – не подходит

Ответ: ОДА

 

Задание ОГЭ №3 "Значение логического выражения"

Теоретическая информация:

Алгебра логики — это математический аппарат, с помощью которого записывают, упрощают и преобразуют логические высказывания, вычисляют их значения.

Высказывание – это предложение, о котором можно сказать, истинно оно или ложно. Высказывания обычно обозначают строчными латинскими буквами a, b, c, d,..., z, w, z, а их истинность/ложность единицей и нулём соответственно:

a = 1 – данная запись говорит нам о том, что высказывание a истинно;

b = 0 – а эта запись – о том, что высказывание b ложно.

1) Отрицание высказывания

Данной операции соответствует логическая связка НЕ и символ ¬

Отрицанием высказывания a называется высказывание ¬a(читается «не а»), которое ложно, если a истинно, и истинно – если a ложно:

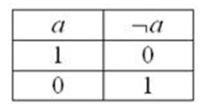
2) Конъюнкция (логическое умножение высказываний)

Данной операции соответствует логическая связка И и символ & либо ^

Конъюнкцией высказываний a и b называют высказывание, которое истинно в том и только том случае, когда истинны оба высказывания a и b:

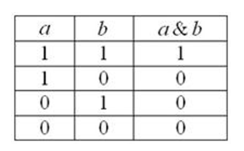
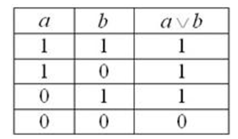
3) Дизъюнкция (логическое умножение высказываний)

Этой операции соответствует логическая связка ИЛИ и символ ˅

Дизъюнкцией высказываний a и b называют высказывание a ˅ b, которое ложно в том и только том случае, когда ложны оба высказывания a и b:

Примеры решения задач:

1. Напишите наименьшее двузначное число x, для которого истинно высказывание:

(ТОЛЬКО ПЕРВАЯ ЦИФРА НЕЧЁТНАЯ) И (ЧИСЛО ДЕЛИТСЯ НА 6) И НЕ (ЧИСЛО ДЕЛИТСЯ НА 7)

Решение: Выражение будет истинным, в том случае, если истинны все, входящие в него, высказывания, так как между высказываниями используется конъюнкция. Число должно быть двухзначным и первая цифра в нём должна быть нечётной. Наименьшая нечётная цифра – «1», значит нам нужно искать число, которое начинается с «1», делится на «6» и не делится на «7». Такое минимальное число – 12.

Ответ: 12

2. Напишите наибольшее число x, для которого ложно высказывание:

(x > 94) ИЛИ (x не делится на 12)

Решение: Выражение должно быть ложным, значит, нам необходимо, чтобы все высказывания, входящие в выражения, были ложны, так как используется дизъюнкция. Для этого нужно выполнить инверсию ко всему высказыванию. Применив инверсию получим высказывание:

(x <= 94) И (x делится на 12)

Наибольшее число, которое меньше или равно 94 – это 84.

Ответ: 84

3. Напишите наибольшее число x, для которого истинно высказывание:

НЕ (x > 47) И НЕ (сумма цифр числа x больше 6)

 Решение: Выражение будет истинным, если будут истинны оба высказывания. Применив инверсию к первому и ко второму высказываниям (так как перед ними стоит инверсия «НЕ», получим высказывание:

(x <= 47) И (сумма цифр меньше или равна 6)

Наибольшее число, которое меньше или равно 47, с суммой цифр больше или равной 6 – это 42.

Ответ: 42

Задание ОГЭ №4 "Формальные описания реальных объектов и предметов"

Теоретический материал:

Граф – это набор вершин (узлов) и связей между ними (рёбер).

Связный граф – это    граф, между любыми    вершинами которого    существует путь.

Дерево – это связный граф без циклов (замкнутых путей).

Дана весовая матрица.

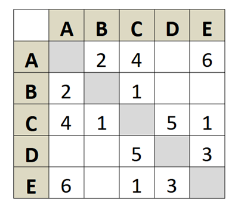
Определите кратчайший путь между пунктами A и D.

Самое эффективное решение - построение дерева возможных путей.

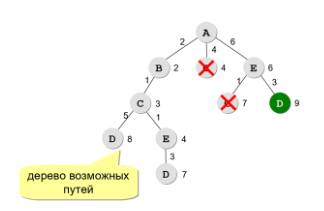
Задания для решения:

1. Учительница Марья Петровна живёт на станции B, а работает на станции D. Чтобы успеть с утра на уроки, она должна ехать по самой короткой дороге. Проанализируйте таблицу и укажите длину кратчайшего пути от станции B до станции D. (6)

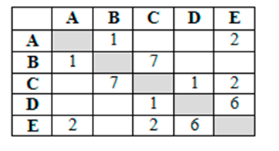
Решение:

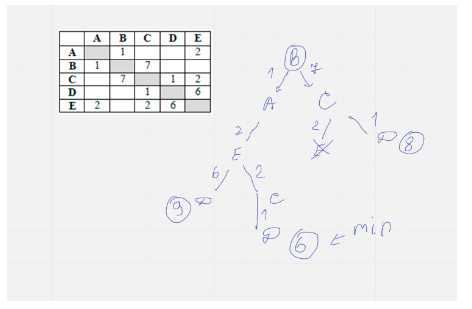
Ответ: 6

2. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт E. Передвигаться можно только по указанным дорогам.


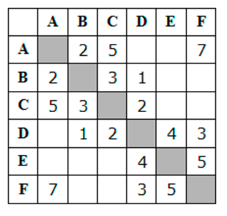
Решение:

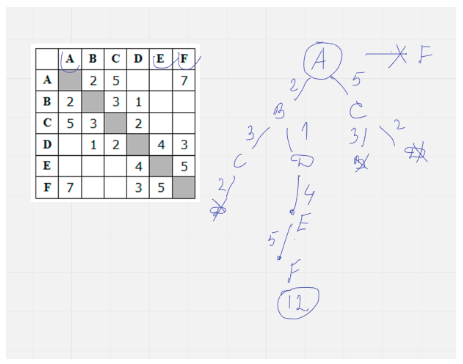
Ответ: 12

3. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Определите длину кратчайшего пути между пунктами A и F, не проходящего через пункт E. Передвигаться можно только по указанным дорогам. 

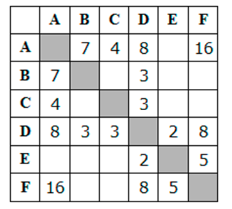
Решение:

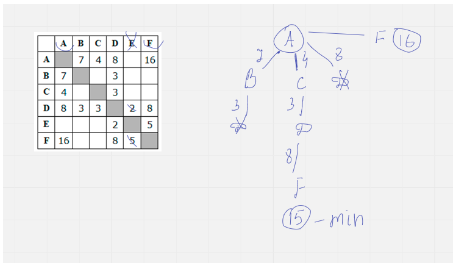
Ответ: 15

 

Задание ОГЭ №5 "Простой линейный алгоритм для формального исполнителя"

Для выполнения данного задания у учащихся должны быть сформированы знания об основах алгоритмизации и исполнителях.

Пример решения задач:

1.У исполнителя Альфа две команды, которым присвоены номера:

1. прибавь 1;

2. умножь на b

(b  — неизвестное натуральное число; b ≥ 2).

Выполняя первую из них, Альфа увеличивает число на экране на 1, а выполняя вторую, умножает это число на b. Программа для исполнителя Альфа  — это последовательность номеров команд. Известно, что программа 11211 переводит число 6 в число 82. Определите значение b.

Решение:

Заметим, что после выполнения первых двух команд мы получаем число 8. Далее, составим и решим уравнение:

8b + 2 = 82

8b = 80

b = 80/10

b = 10

 

Ответ: 10.

2. У исполнителя Бета две команды, которым присвоены номера:

  1. прибавь b

  2. умножь на 3

(b – неизвестное натуральное число)

Выполняя первую из них, Бета увеличивает число на экране на b, а выполняя вторую, умножает это число на 3. Программа для исполнителя Бета – это последовательность номеров команд. Известно, что программа 21212 переводит число 8 в число 360. Определите значение b. 

Решение:

Заметим, что после выполнения первой команды мы получаем число 8 * 3 = 24. Далее, составим и решим уравнение:

((24 + b) * 3 + b) * 3 = 360

(72 + 4b) * 3 = 360

216 + 12b = 360

12b = 144

b = 12

 Ответ: 12

3. У исполнителя Омега две команды, которым присвоены номера:

1. прибавь 3;

2. раздели на b

(b  — неизвестное натуральное число; b ≥ 2).

Выполняя первую из них, Омега увеличивает число на экране на 3, а выполняя вторую, делит это число на b. Программа для исполнителя Омега  — это последовательность номеров команд. Известно, что программа 11121 переводит число 46 в число 8. Определите значение b.

Решение.

Заметим, что после выполнения первых трёх команд мы получаем число 55. Далее, составим и решим уравнение:

(55 / b) + 3 = 8

(55 / b) = 5

b = 11

 Ответ: 11.

4. У исполнителя Квадратор две команды. которым присвоены номера:

1.  возведи в квадрат

2.  прибавь 3

Первая из них возводит число на экране во вторую степень, вторая увеличивает его на 3.

Составьте алгоритм получения из числа 1 числа 25, содержащий не более 5 команд. В ответе запишите только номера команд.

 (Например, 12221  — это алгоритм:

возведи в квадрат

прибавь 3

прибавь 3

прибавь 3

возведи в квадрат,

который преобразует число 2 в 169.)

 Если таких алгоритмов более одного, то запишите любой из них.

 Решение.

Не любое число является квадратом целого числа, поэтому, если мы пойдём от числа 25 к числу 1, тогда однозначно восстановим программу. Полученные команды будут записываться справа налево.

Число 25 является квадратом. Если образовали его, пользуясь первой командой (25  =  5 · 5), то предшествующим являлось число 5. Число 5 с помощью второй команды получилось из числа 2, к которой дойти от 1, используя данные команды, невозможно.

 1.  Значит, 25 было получено добавлением трёх к числу 22: 22 + 3 = 25 (команда 2).

2.  Число 22 не является квадратом, поэтому оно получено добавлением трёх к числу 19: 19 + 3 = 22 (команда 2).

3.  Число 19 не является квадратом, поэтому оно получено добавлением трёх к числу 16: 19 = 16 + 3 (команда 2).

4.  Число 16 является квадратом числа 4: 16 = 4 · 4 (команда 1).

5.  Число 4 можно получить возведением в квадрат числа 2 (команда 1) либо прибавлением 3 к числу 1 (команда 2). Поскольку исходным должно быть число 1, а в программе должно быть не более пяти команд, выбираем второй вариант: 4 = 1 + 3 (команда 2).

Искомая последовательность команд: 21222.

Ответ: 21222

5. У исполнителя Вычислитель две команды, которым присвоены номера:

1. умножь на b

2.  прибавь 2

(b  — неизвестное натуральное число)

Первая из них увеличивает число на экране в b раз, вторая увеличивает его на 2.

Известно, что программа 12221 переводит число 1 в число 91. Определите значение b.

Решение.

Cоставим и решим уравнение:

(1b + 6) · b = 91.

b² + 6b − 91 = 0

Решив, квадратное уравнение, получим:

b₁=7; b₂=−13.

Отрицательные корни рассматривать не нужно.

Соответственно, b  =  7. 

Ответ: 7.

 

 

 

 

Задание ОГЭ №6 "Программа с условным оператором"

Теоретический материал:

Условный оператор.

Условный оператор реализует выполнение определённых команд при условии, что некоторое логическое выражение (условие) принимает значение «истина» true. В большинстве языков программирования условный оператор начинается с ключевого слова if (в переводе с англ. — «если»). Встречаются следующие формы условного оператора ­-- с одной ветвью и двумя.

При выполнении условного оператора с одной ветвью if <условие> then <команды> end вычисляется условие, и если оно истинно, то выполняются команды до ключевого слова end, в противном случае выполнение программы продолжается со следующей за условным оператором команды.

 

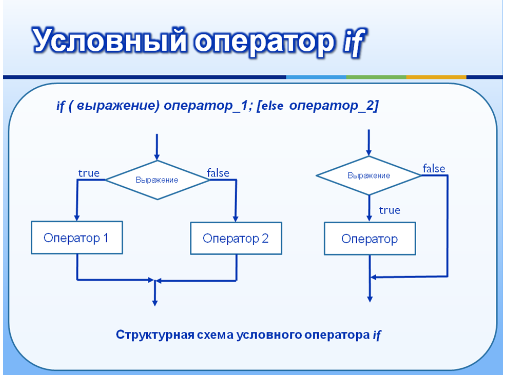
Логические оператор "or", встречающийся в условии,  соответствует дизъюнкции, оператор "and" соответствует конъюнкции.

Задания по теме "Программа с условным оператором".
1. Ниже приведена программа, записанная на пяти языках программирования.

Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:

(9, 9); (9, 10); (8, 5); (11, 6); (–11, 10); (–5, 9); (–10, 10); (4, 5); (8, 6).

Сколько было запусков, при которых программа напечатала «YES»? 

Решение.

Заметим, что программа напечатает «YES», если одна из введённых переменных s и t будет меньше 9. Значит, было 7 запусков, при которых программа напечатала «YES». В качестве значений переменных s и t в этих случаях вводились следующие пары чисел:

(8, 5); (11, 6); (–11, 10); (–5, 9); (–10, 10); (4, 5); (8, 6).

Ответ: 7

 2. Ниже приведена программа, записанная на пяти языках программирования.

Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:

(13, 2); (11, 12); (–12, 12); (2, –2); (–10, –10); (6, –5); (2, 8); (9, 10); (1, 13).

Укажите наименьшее целое значение параметра A, при котором для указанных входных данных программа напечатает «NO» восемь раз.

Решение.

Заметим, что программа напечатает «NO», если переменная t будет меньше или равна 12, а переменная s будет меньше или равна А.

Из первой части условия получаем, что при вводе значений s и t (1, 13) программа напечатает «YES» вне зависимости от значения A. При отрицательных значениях A программа будет выводить «YES» больше одного раза.

Заметим, что при A  =  1 программа напечатает «NO» два раза, при 2 ≤ A ≤ 5 программа напечатает «NO» четыре раза, при 6 ≤ A ≤ 8 программа напечатает «NO» пять раз, при 9 ≤ A ≤ 10 программа будет печатать «NO» шесть раз, при 11 ≤ A ≤ 12 программа будет печатать «NO» семь раз, а при A  =  13 программа будет печатать «NO» восемь раз. Таким образом, ответ  — 13.

Ответ: 13.

3. Ниже приведена программа, записанная на пяти языках программирования.

Было проведено 10 запусков этой программы, при которых в качестве значений переменных x и y вводились следующие пары чисел:

(105, 100); (95, 110); (100, 95); (95, 90); (105, 90); (85, 110); (100, 110); (85, 105); (85, 95); (90, 100)

Сколько было запусков, при которых программа напечатала «НЕТ»? (2)

Решение.

Заметим, что программа напечатает «НЕТ», если переменная y будет больше 100 и x будет меньше или равно 90. Причём, обязательно нужно обратить внимание на то, что первой вводится переменная x, а второй переменная y, а в условии они записаны в обратном порядке. Значит, было 2 запуска, при которых программа напечатала «НЕТ». В качестве значений переменных x и y в этих случаях вводились следующие пары чисел:

(85, 110); (85, 105)

Ответ: 2

 

Скачано с www.znanio.ru