Разбор заданий ОГЭ информатика 7-10 вопрос

Задание ОГЭ №7 "Информационно-коммуникационные технологии"

Теоретический материал:

IP-адреса

Каждый узел имеет уникальный адрес!

IP-адрес содержит номер сети и номер узла в этой сети.

Сайт (веб-сайт) – это группа веб-страниц, которые расположены на одном сервере, объединены общей идеей и связаны с помощью гиперссылок.

Веб-сервер – это программа, которая обеспечивает работу сайтов: приём запросов и выдачу ответов по протоколу HTTP или HTTPS.

Браузер – это программа для просмотра веб-страниц на экране.

Адрес документа в Интернете

URL (Uniform Resource Locator) – универсальный адрес документа в Интернете.

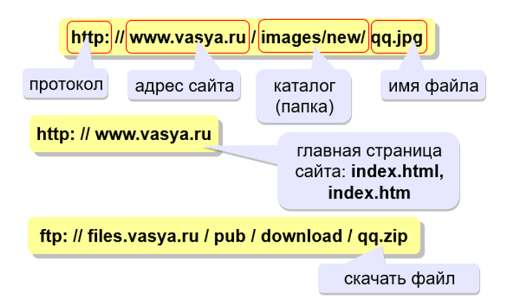
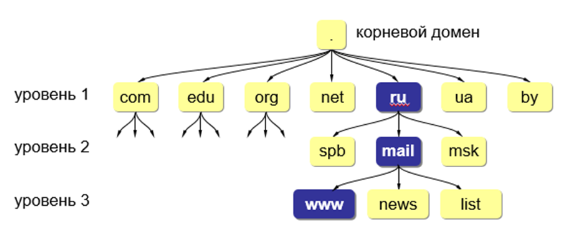
Доменные имена.

Домен – это группа символьных адресов в Интернете.

Задания по данной теме:

1. Доступ к файлу img.bmp, находящемуся на сервере pic.kz, осуществляется по протоколу http. Фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет.

 A)  img

Б)  /

B)  kz

Г)  ://

Д)  http

Е)  .bmp

Ж)  pic.

Решение.

Напомним, как формируется адрес в сети Интернет. Сначала указывается протокол (как правило это «ftp» или «http»), потом «://», потом сервер, затем «/», название файла указывается в конце. Таким образом, адрес будет следующим: http://pic.kz/img.bmp. Следовательно, ответ ДГЖВБАЕ.

Ответ: ДГЖВБАЕ.

 

2. Доступ к файлу book.jpg, находящемуся на сервере biblioteka.ru, осуществляется по протоколу http. Фрагменты адреса файла закодированы цифрами от 1 до 7. Запишите последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет.( 4237651)

1) .jpg         2) ://
3) biblioteka. 4) http
5) book        6) /
7) ru

Решение.

Напомним, как формируется адрес в сети Интернет. Сначала указывается протокол (как правило это «ftp» или «http»), потом «://», потом сервер, затем «/», название файла указывается в конце. Таким образом, адрес будет следующим: http://biblioteka.ru/book.jpg. Следовательно, ответ 4237651.

Ответ: 4237651

3. Фотография Кремля хранится на компьютере по адресу C:\photo\kremlin.png. Данную фотографию переместили в каталог monuments сайта photo.ru, доступ к которому осуществляется по протоколу http. В таблице фрагменты адреса файла закодированы числами от 1 до 8. Запишите последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет.( 531864672)

  1) photo.    2) .png  3) ://
  4) monuments 5) http  6) /
  7) kremlin   8) ru

Решение:

Напомним, как формируется адрес в сети Интернет. Сначала указывается протокол (как правило это «ftp» или «http»), потом «://», потом сервер, затем «/», название файла указывается в конце. Так как фотографию переместили в каталог monuments, то после имени сайта будет указано имя каталога. Таким образом, адрес будет следующим: http://photo.ru/monuments/ kremlin.png. Следовательно, ответ 5318646672.

Ответ: 5318646672

4. На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г:

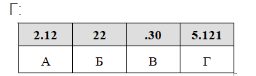
Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

Решение.

IP-адрес представляет собой четыре разделённых точками числа, каждое из которых не больше 255.

Под буквой В указано «.30». Так как числа в IP-адресе не могут быть больше 255, нельзя добавить в конце этого числа еще один разряд. Следовательно, этот фрагмент  — последний.

Рассмотрим фрагмент под буквой Б. Так как числа в IP-адресе не могут быть больше 255, фрагмент Б должен быть на первом месте.

В конце фрагмента Г  — число 121, отделенное точкой. Так как в IP-адресе не может быть числа, большего 255, то за фрагментом Г должен следовать фрагмент, начинающийся с точки. Значит, фрагмент Г идет перед фрагментом В.

Следовательно, ответ БАГВ.

 

Задание ОГЭ №8 "Запросы поисковых систем с использованием логических выражений"

Теоретическая информация:

Множество – некоторый набор элементов, каждый из которых отличается от остальных.

пустое множество: Ø

конечное число элементов: буквы русского алфавита

бесконечное число элементов: натуральные числа

Как задать множество?

•   перечислением элементов: {Вася, Петя, Коля}

•   логическим выражением: {x: x > 0}

Изображение множеств

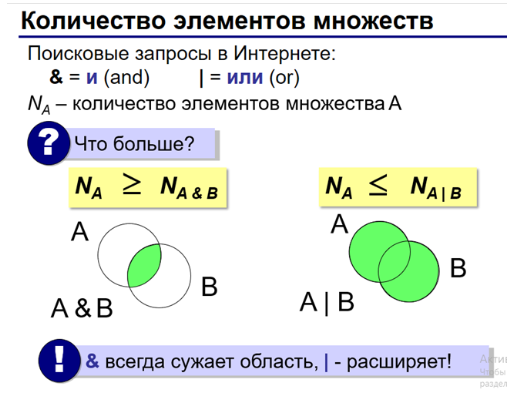
Множества можно изобразить с помощью диаграмм Эйлера - Венна.

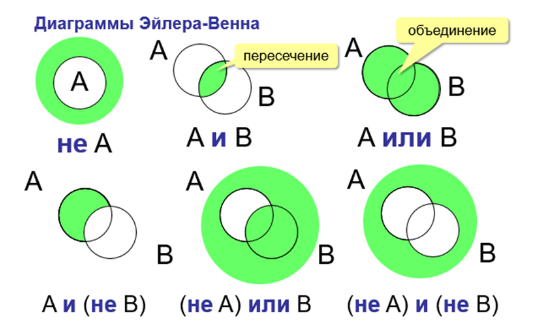
Для определения количества элементов множеств можно воспользоваться формулой включений и исключений. Помнить нужно о том, что "ИЛИ" всегда расширяет множество, а "И" - сужает.

Примеры решения задач:


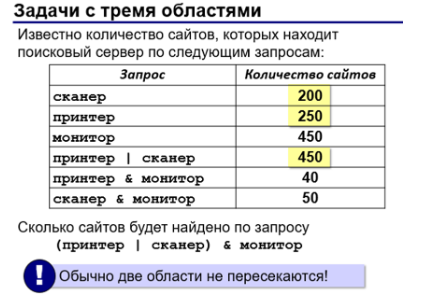
Тогда по формуле включений и исключений получим: 200 + 100 - 50 = 150

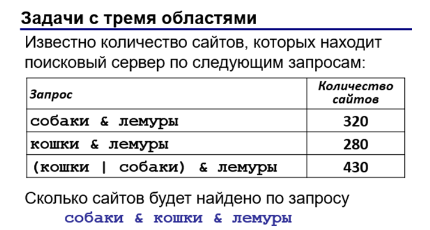
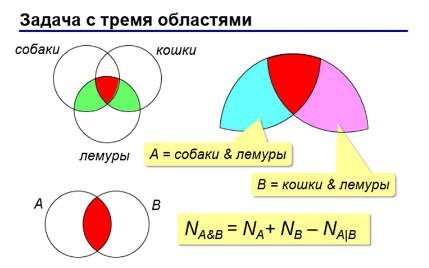
Тогда получаем: 320 + 280 - 430 = 170

Другой способ решения: 


Ещё один пример:

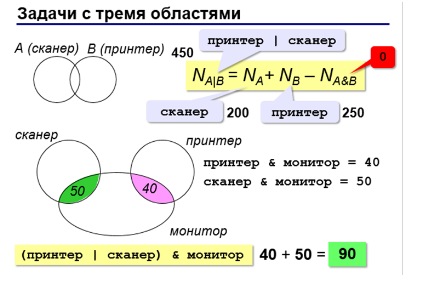
Решение задач:

1. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И»  — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

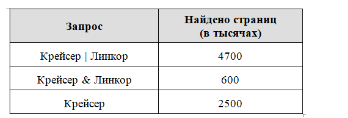
Какое количество страниц (в тысячах) будет найдено по запросу Линкор?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение.

По формуле включений и исключений имеем:

m(Крейсер | Линкор) = m(Крейсер) + m(Линкор) − m(Крейсер & Линкор)

m(Линкор) = m(Крейсер | Линкор) − m(Крейсер) + m(Крейсер & Линкор) = 4700  — 2500 + 600  =  2800.

 Ответ: 2800.

2. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И»  — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

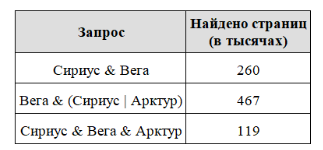
Какое количество страниц (в тысячах) будет найдено по запросу Вега & Арктур ? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение: Так как запрос «Вега» входит во все запросы и в сам вопрос, то этот запрос мы можем сократить. Тогда получиться следующий запрос:

 

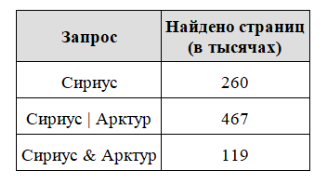
Какое количество страниц (в тысячах) будет найдено по запросу Арктур ?

 По формуле включений и исключений имеем:

m(Сириус | Арктур) = m(Сириус) + m(Арктур) − m(Сириус & Арктур)

m(Арктур) = m(Сириус | Арктур) − m(Сириус) + m(Сириус & Арктур) = 467 — 260 +119  =  326.

Ответ: 326.

4. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И»  — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

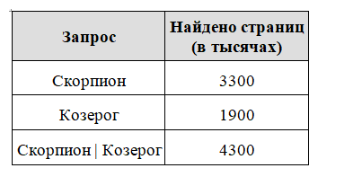
Какое количество страниц (в тысячах) будет найдено по запросу

Скорпион & Козерог?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение.

Представим таблицу в виде кругов Эйлера. Пусть Скорпион  — круг 1, Козерог  — круг 3. Тогда задача  — найти количество элементов N в области 2 : N₂. По таблице известно:

N₁ + N₂  =  3300 (1),

N₂ + N₃  =  1900 (2),

N₁ + N₂ + N₃  =  4300.

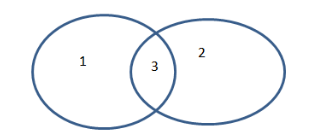
Подставим первое уравнение в третье и найдём N₃: N₃  =  4300 − 3300  =  1000. Таким образом, по запросу Скорпион & Козерог будет найдено N₂  =  1900 − 1000  =  900 тысяч страниц.

Ответ: 900.

Задание ОГЭ №9 "Анализирование информации в виде схем"

Как правило для анализа представлен ориентированный граф, в котором нужно определить количество всех дорог из одного пункта в другой. Часто условие дополняется "посещением" или "непосещением" некоторых пунктов.

Решать данное задание можно либо по формулам, начиная рассматривать граф "с конца", либо определяя количество входящих путей в каждый пункт.

Примеры решения задач:

1. На рисунке  — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И, проходящих через город В?

Решение. Количество путей до города Х  =  количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом если путь должен не проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

А = 1

Б = А = 1

В = А + Б + Г= 4

Д = 1

Е = В = 4 (Б не учитываем, должны пройти через точку В)

Ж = В + Е = 4 + 4 = 8 (Не учитываем Г, Д, З

И = Е + Ж = 4 + 8 = 12 (Не учитываем З)

 Ответ: 12

2. На рисунке  — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт К, не проходящих через пункт В?

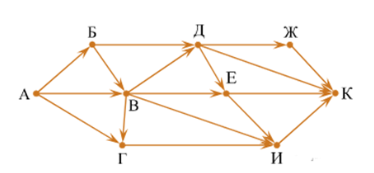
Решение. Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.

При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.

Примечание. Необходимо найти количество различных путей из города А в город К, не проходящих через город В.

С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:

А = 1.

Б = А = 1.

Г = А = 1.

Д = Б = 1.

Е = Д = 1 (В не учитываем, поскольку путь не должен проходить через город В).

Ж = Д = 1.

И = Г + Е = 2.

К = Ж + Е + И + Д = 5.

Ответ: 5.

https://youtu.be/tKCWpREbPOY

 

Задание ОГЭ № 10 "Сравнение чисел в различных системах счисления"

Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также соответствующие правила выполнения операций с этими числами.

Позиционная система: значение цифры определяется ее позицией в записи числа.

Алфавит системы счисления — это используемый в ней набор цифр.

Основание системы счисления — это количество цифр в алфавите (мощность алфавита).

Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.

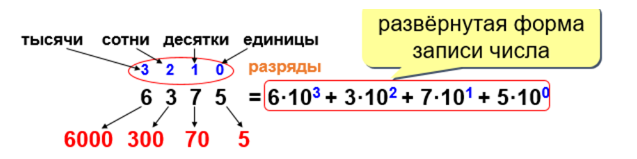
Перевод в десятичную систему счисления осуществляется через развёрнутую запись числа.


Перевод из десятичной системы счисления в любую другую систему счисления осуществляется при помощи деления на цело на основание новой системы счисления (p)

Делим число на p (основание новой системы счисления), отбрасывая остаток на каждом шаге, пока не получится 0. Затем надо выписать найденные остатки в обратном порядке.

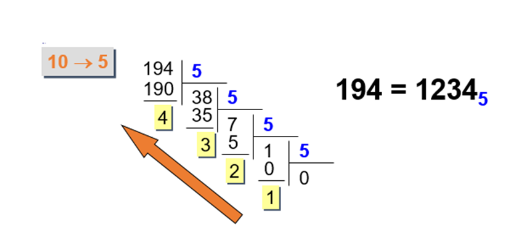
Для перевода из двоичной в восьмеричную и шестнадцатеричную системы можно воспользоваться представлением чисел 8 и 16 с помощью двоичных разрядов, соответствующих степеням двойки.

Восьмеричная система счисления:


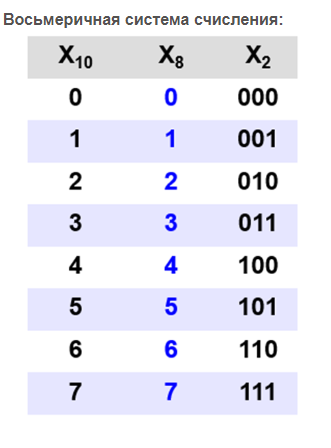
Перевод в двоичную систему счисления:


Перевод из двоичной в восьмеричную:

Шестнадцатеричная система счисления

 

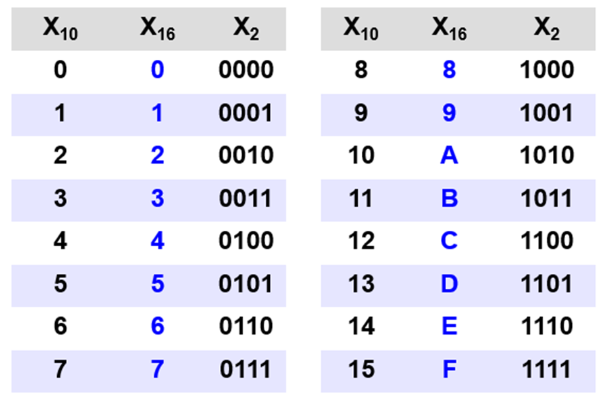
Перевод в двоичную систему

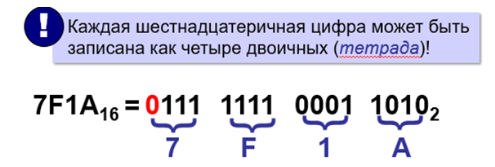
Перевод из двоичной системы

Примеры решения задач:

1.    Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

14₁₆, 26₈, 11000₂.

Решение.

Переведём все числа в десятичную систему счисления:

1.  14₁₆  =  20₁₀;

2.  26₈  =  22₁₀;

3.  11000₂  =  24₁₀.

Таким образом, наибольшим среди этих трёх чисел является число 24.

Ответ: 24

2. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

47₁₆, 120₈, 1001011₂.

Решение.

Переведём все числа в десятичную систему счисления:

1.  47₁₆  =  71₁₀;

2.  120₈  =  80₁₀;

3.  1001011₂  =  75₁₀.

Таким образом, наименьшим среди этих трёх чисел является число 71.

 Ответ: 71.

3.  Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, сумма цифр которого в восьмеричной записи наименьшая. В ответе запишите сумму цифр в восьмеричной записи этого числа.

55₁₀, 83₁₀, 91₁₀.

Решение.

Переведём все числа в восьмеричную систему счисления:

1.  55₁₀ = 67₈ , сумма цифр  — 6 + 7 = 13;

2.  83₁₀ = 123₈ , сумма цифр  — 1 + 2 + 3 = 6;

3.  91₁₀ = 133₈ , сумма цифр  — 1 + 3 + 3 = 7.

 Ответ: 6

 

Скачано с www.znanio.ru