РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ

разложение многочлена на множители способом группировки

Цели: познакомить учащихся со способом группировки разложения многочлена на множители; формировать умение применять этот способ.

Ход урока

I. Устная работа.

1. Вычислите.а) (–0,1)² + (–0,2)²;                  в) – (0,1 – 0,2)²;                   д) ;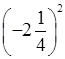 

б) (–0,1 – 0,2)²;                          г) 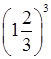;                              е) .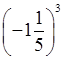

2. Разложите многочлен на множители.

а) ab – a²b;                     в) 6у⁵ – 9у²;                          д) 3 (a – b) – x (a – b);

б) 2х³ + 4х;                      г) n²m³ + n³m;                       е) (у + 2)² – х (у + 2).

II. Объяснение нового материала.

Затем можно рассмотреть пример 2 из учебника.

1) ху + 4х – 2у – 8 = (ху + 4х) – (2у + 8) = х (у + 4) – 2 (у + 4) =
= (у + 4) (х – 2).

2) ху + 4х – 2у – 8 = (ху – 2у) + (4х – 8) = у (х – 2) + 4 (х – 2) =
= (х – 2) (у + 4).

3) ху + 4х – 2у – 8 = (ху – 8) + (4х – 2у) – не даёт результата.

III. Формирование умений и навыков.

1. № 708, № 709.

2. № 711 (а, в, д, з).

Решение:

а) х³ + х² + х + 1 = (х³ + х²) + (х + 1) = х² (х + 1) + (х + 1) = (х + 1) (х² + 1).

в) а⁴ + 2а³ – а – 2 = (а⁴ + 2а³) – (а + 2) = а³ (а + 2) – (а + 2) =
= (а + 2) (а³ – 1).

д) а² – ab – 8а + 8b = (а² – ab) – (8а – 8b) = а (a – b) – 8 (а – b) =
= (a – b) (а – 8).

з) kn – mn – n² + mk = (kn + mk) – (mn + n²) = k (n + m) – n (m + n) =
= (m + n) (k – n).

IV. Итоги урока.

Домашнее задание: № 710; № 711 (б, г, е); № 712.