РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ3

разложение многочлена на множители способом группировки

Цели: продолжить формирование умения применять способ группировки при разложении многочлена на множители; проверить уровень усвоения материала.

Ход урока

I. Формирование умений и навыков.

Все задания можно разбить на две группы. В 1-ю группу войдут задания на применение способа группировки при доказательстве тождеств и нахождении значений выражений. А во 2-ю группу войдут сложные задания, в которых нужно разложить на множители многочлены способом группировки.

1-я группа

1. № 713.

Важно, чтобы учащиеся поняли, что непосредственная подстановка данных значений переменных приведет к громоздким вычислениям.

Решение:

а) p²q² + pq – q³ – p³ = (p²q² – q³) + (pq – p³) = q² (p² – q) + p (q – p²) =
= q² (p² – q) – p (p² – q) = (p² – q) (q² – p).

При p = 0,5 и q = –0,5:

(p² – q) (q² – p) = (0,25 + 0,5) (0,25 – 0,5) = 0,75 · (–0,25) =
=.

б) 3х³ – 2у³ – 6х²у² + ху = (3х³ – 6х²у²) – (2у³ – ху) = 3х² (х – 2у²) –
– у (2у² – х) = 3х² (х – 2у²) + у (х – 2у²) = (х – 2у²) (3х² + у).

При x =  и у = :

(х – 2у²) (3х² + у) =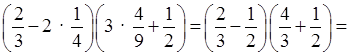

2. № 715.

Заметим, что, исходя из логики доказательства тождеств, можно преобразовать левую часть равенства в правую (для этого многочлен нужно разложить на множители), а можно преобразовать правую часть в левую (для этого нужно перемножить двучлены).

2-я группа

1. № 716.

До этого учащиеся использовали способ группировки для разложения на множители многочленов, состоящих из четырёх членов. Нужно обратить внимание учащихся, что это самый распространенный случай применения данного способа. Но иногда способ группировки может быть использован при разложении на множители многочленов с другим количеством членов.

Решение:

а) (bd – ad – cd) =

б) (bx² + by² – b) =

в) (cn² – cp + cp²) =

г) (ax – ab + a) =

2. № 718 (а, в).

Прежде  чем  решать  этот  номер,  нужно  рассмотреть  пример  3  из учебника.

Решение:

а) x (x + 1) +
+ 5 (x + 1) = (x + 1) (x + 5).

в) a (a – 1) –
– 4 (a – 1) = (a – 1) (a – 4).

II. Итоги урока.

– Какие вы знаете способы разложения многочлена на множители?

– Опишите алгоритм способа группировки.

– Сколько членов содержали многочлены, которые мы раскладывали на множители способом группировки?

Домашнее задание: № 714; № 717; № 718 (б, г).