Тема урока

«Тела вращения.

Цилиндр. Конус.

Сфера. Шар»

Что такое тело вращения?

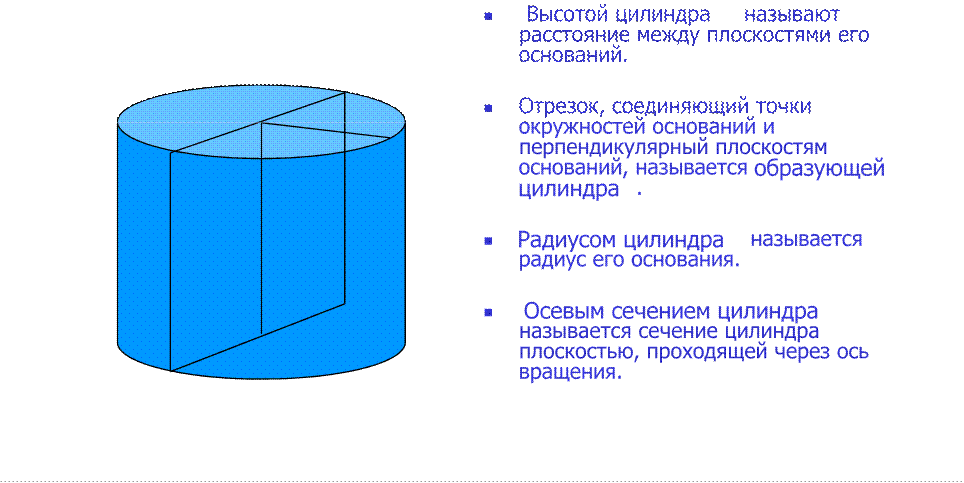
Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.

Виды тел вращения

n   Шар — образован полукругом, вращающимся вокруг диаметра разреза

n   Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон

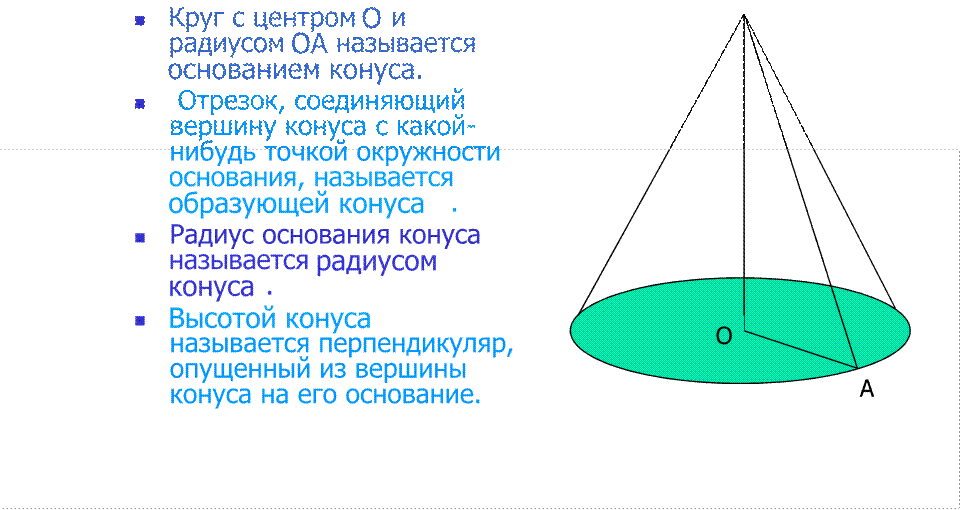
n   Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов

n   Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его 

n

При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).

ЦИЛИНДР

Элементы цилиндра

Развертка цилиндра

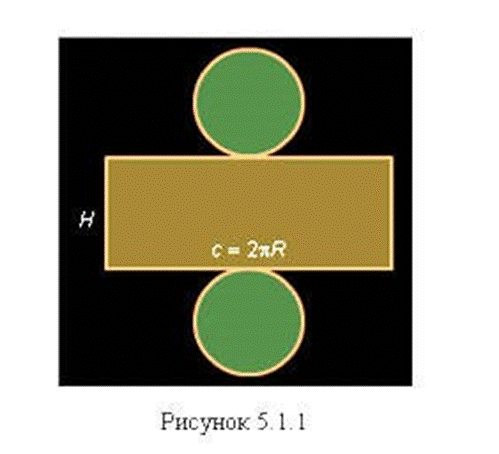На рисунке показана развертка цилиндра. Разверткой боковой поверхности цилиндра является прямоугольник со сторонами Hи C, где H

– высота цилиндра, а C– длина окружности основания.

Объем и площадь поверхности цилиндра

n Объем:

V=S_оснH=πR²H

S= 2Sосн+ Sбок.п.=2

πR(R+H)

конус

Элементы конуса

Развертка конуса

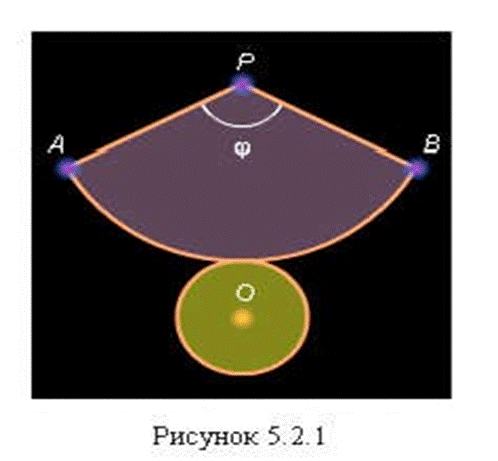Разверткой боковой поверхности конуса  является круговой сектор

Объем и площадь поверхности конуса

n   ℓ - длина

                        S_бок.п.=πRℓ                 образующей конуса

n   Площадь полной поверхности:

S= Sосн+ Sбок.п.= πR(R+ℓ)

Сфера и шар

n   Множество всех точек пространства, одинаково удаленных на расстояние Rот данной точки O, называется сферой.

n   Множество всех точек пространства, удаленных от данной точки Oна расстояние, не большее R, называется шаром.

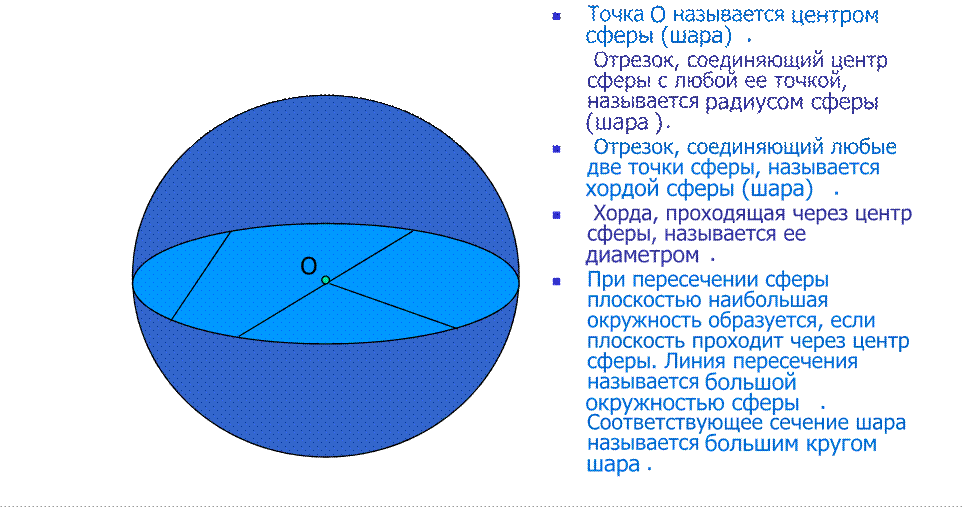Элементы сферы и шара

n

Объем и площади поверхностей шара и сферы

n  Площадь сферы радиуса R: S=4πR²

n  Площадь сферического сегмента радиуса R и высоты Н: S= 2πRH

n  Объем шара: V= ⁴/₃πR³

n  Объем шарового сектора: V=⅔πR²H

Тор

ТОР (от лат. torus выпуклость), геометрическое тело, образуемое вращением круга вокруг непересекающей его и лежащей в одной с ним плоскости прямой, другое название – полноторие.

Приблизительную форму тора имеет спасательный круг, баранка.

Поверхность, ограничивающую тор, иногда также называют тором.

Объем и площадь поверхности тора

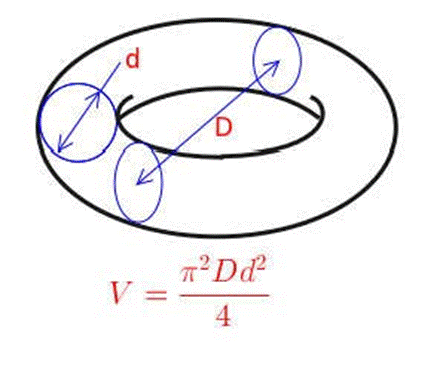
n Площадь поверхности: S=π²Dd n Объем тора:V=¹/₄π²Dd²

где  D - середина между наружным диаметром тора и диаметром внутреннего отверстия и d - диаметр

Домашнее задание

n   В учебнике выучить п. 129-131 на стр.

319-322

n   Решить задачи №1213 (разобрать решение в учебнике), 1214а, 1220 а, 1226а.

n

n   Ответить на вопросы (устно) 15-26 на стр.327-328 учебника