Реализация генератора гаммы на регистрах сдвига.docx

Реализация генератора гаммы на регистрах сдвига

Общая идея:

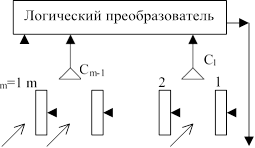C₀ = 1

С

C_i = {0, 1}

Рис. 1

элемент (звено) задержки информации в регистре сдвига на один такт (тактовый генератор не показан)

C

q         

выход = q×C – элемент умножения

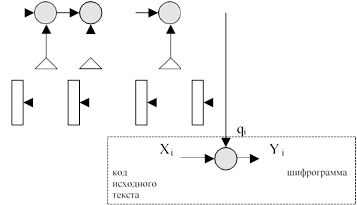Например, для полинома 3-го порядка q_i = q_i-1 + q_i-3

3

q_i    Рис. 3

Более криптостойка нелинейная схема с дополнительным ЛП.

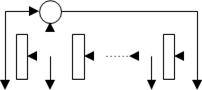Рис. 4

Y

X

Комбинированные генераторы ПСП бит на регистрах сдвига с обратной связью.

1)      Схема Джеффа

AND

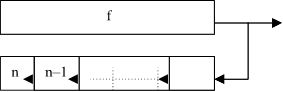
2)      Схема Брюса

AND

XOR

Рис. 5

Рис. 6

арифметический сумматор Генератор ПСП бит с внутренней нелинейной логикой

ПСП

1, S³порог

0, S<порог

Рис. 7

Генератор ПСП бит с внешней нелинейной логикой

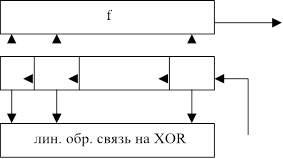ПСП

Рис. 8

ПСП максимальной длины для регистров сдвига с m звеньями

При m = 100 максимальная длина гамм равна 2¹⁰⁰ – 1. Для передачи её со скоростью

1 Мбайт/с период повторится лишь через ~ 10¹⁶ лет.

Однако если 2m бит исходного текста известны хакеру, то 2m бит гаммы вычисляются просто, и можно определить расположение отводов С_i регистра и его начальное состояние, если известно m.

[Диффи У., Хеллман М. Защищённость и имитостойкость. Введение в криптографию//ТИНЭР – 1979, т. 67, №3, стр. 71-104]

Распределение отводов можно определить, так как:

+1   = (  × S  )mod 2 ,                  (6)

где S_i – вектор-столбец из m символов состояния регистра в i-й момент; А – матрица m*m положений отводов,

1-ая строка – последовательность отводов, непосредственно под главной диагональю располагаются единицы, а в остальных позициях нули.

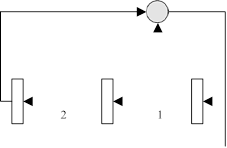
Например, для трехразрядного регистра (Рис. 3)

21C3  011

A010  001

100  100

Зная 2m бит гаммы, можно за m³ итераций обратить формулу (6) и найти отводы.