Реферат Математические понятия в начальной школе

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Забайкальский государственный университет»

(ФГБОУ ВПО «ЗабГУ»)

Психолого – педагогический факультет

Кафедра ТМДНО

РЕФЕРАТ

 

по дисциплине: «Теретическое мышление младших школьников в процессе образовния»

на тему «Математические понятия в начальной школе»

 

Выполнил

 

 

 

 

 

 

 

 

 

Чита

2021

СОДЕРЖАНИЕ

1.                 Понятия и представления при изучении математики ……………...3 

2.                 Математические понятия и их виды ……………………………….11

3.                 Определение        математических   понятий.     Требования          к  определению ……………………………………………………………. …..13

4.      Виды      действий,      используемых      при          формировании 

математических понятий  ……………………………………………………20   

Список литературы……………………………………………… …………..44   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Понятия и представления при усвоении математики.

Понятия являются одной из главных составляющих содержания любого предмета. 

Формирование понятия – сложный психологический процесс, начинающийся с образования простейших форм чувственного познания, ощущений, и протекающий часто по следующей схеме: ощущение – восприятие  -  представление – понятие.

Представлением называют вторичный образ предмета или явления.  В зависимости от того, как возникает этот образ можно выделить 2 группы представлений: 

 

Представления

 

 

представления памяти                  представления воображения

 

Представления памяти  возникают у человека в основном благодаря ощущениям и восприятию. Но в отличие от образов ощущений и восприятий, т.е. непосредственных результатов этих процессов, образ представлений может быть отсрочен во времени и пространстве от ощущения и восприятия, он как бы извлекается человеком из памяти. Ведь для того чтобы что-то представить, нам не надо непосредственно видеть какой-то предмет.

Представления воображения создаются при помощи воссоздающего воображения. Такие представления возникают у человека в результате преобразования в его памяти имеющихся образов. Образ представлений в этом случае создается при помощи словесной инструкции или демонстрации каких-то действий и образцов. Например: «Голубой марлин – это одна из крупнейших рыб, обитающих в мировом океане. Его максимальная масса тела 818 кг, а длина – 5 м. Марлин  имеет длинный прямой вырост на верхней челюсти. Тело хищника окрашено контрастно: верхняя часть, с двумя спинными плавниками, имеет сине-черный окрас, нижняя – серебристобелая. На каждом боку имеется около 15 поперечных телу белых полос, состоящих из точек ». У человека, прочитавшего описание,  возникает образ рыбы, которую он до этого никогда не видел. При этом особую значимость в понимании словесного объяснения играет употребление различных признаков (цвет, форма, размер), которые всеми людьми воспринимаются одинаково.

И тот и другой вид представлений имеет место в школьном курсе математики. Например, к представлениям памяти можно отнести образы различных геометрических фигур. К представлениям воображения – представления о возможных случаях взаимного расположения фигур.

Исходя из природы появления представлений, можно определить их основные характеристики:

1.                  Субъективность представлений, т.к. жизненный опыт и воспоминания людей сугубо индивидуальны. Если попросить группу людей представить лимон и описать картинку, которую они воссоздали в воображении, описания будут разными. Кто-то увидел нарезанный, кто-то висящий на дереве, но большинство – один, как рисуют на картинках в детском лото, именно это подсказывает вторую характеристику.

2.                  Обобщенность. У  большинства людей образ представленного лимона будет суммировать образы всех лимонов, которые они видели когдато в жизни, поэтому мала вероятность того, что кто-то увидел его зеленым или гнилым.

3.                  Яркость.

4.                  Четкость.

5.                  Полнота.

6.                  Детализация.

Указанные характеристики зависят от условий восприятия, эмоционального настроя и индивидуального опыта конкретного человека.

Представления делятся на виды по степени обобщенности образа: единичные (образ конкретного треугольника АВС), общие (образ треугольника) и есть столь обобщенные образы предмета, что они отражают его схематически, например, числа, знаки, различные условные обозначения.

Главным фактором, который влияет на качество формируемых представлений, является активное оперирование учащимися изучаемым объектом.

Проблемы формирования представлений при обучении математике.

1.                 Далеко не все предметы и явления можно представить. В связи с этим создается редкая в обыденной жизни ситуация, когда учителю необходимо формировать понятие при отсутствии более ранних чувственных форм познания, имеющих образную природу. Поэтому особо возрастает роль графических способов представления материала и решения задач, когда учитель использует не реальные образы, а их подчас искусственно созданные заменители.

2.                 В курсе математики встречаются ситуации, когда чувственная ступень познания играет меньшую роль, и наглядность из средства, способствующего формированию понятия, становится тормозящим фактором. Например, бесконечность множества чисел на любом отрезке числовой прямой не подкрепляется, а, наоборот, опровергается конкретным образом конечного отрезка. 

3.                 Учителям математики свойственно мало внимания уделять формированию у учащихся необходимых математических представлений.

Переход от представлений к понятиям совершается при помощи мыслительных операций, прежде всего, обобщения и абстрагирования.

Понятие – это форма мышления о целостной совокупности существенных и несущественных свойств объектов реального мира, в частности, и математических объектов. 

Сравнивая понятия и представления, можно выделить следующие их отличия. 

Представление	Понятие
Вторичный образ предмета	Мысль о предмете, выраженная в словах
Обобщает как существенные, так и несущественные свойства предметов и явлений	Обобщает     только       существенные свойства предметов
Субъективно, т.к. складывается в индивидуальном опыте человека	Складывается в теоретической и практической деятельности многих поколений
Одно и то же представление у разных людей         различно    по           точности, яркости, полноте и т.п.	У больших групп людей понятия одинаковы
Не все явления и процессы можно представить	Мыслить в понятиях можно о любых процессах и явлениях.

 

Для формирования математических понятий необходимо понимание математического объекта, который в понятии характеризуется благодаря применению определенных умственных действий.

Математика изучает окружающий нас мир, природные и общественные явления, но изучает лишь особые стороны этих явлений. Например, нужно рассчитать, сколько кафельных плиток необходимо купить для облицовки стены, если известно, что плитка имеет форму квадрата со стороной  20см. В этом случае безразлично, какого цвета стена или из какого материала она сделана. Важно знать лишь форму и размер этой стены. В этом случае отвлекаемся от всех свойств рассматриваемого предмета и выделяем только его форму и размер. В результате такого абстрагирования получаем математический объект - геометрическую фигуру. 

Вообще математические объекты – это результат выделения из предметов и явлений окружающего мира особых количественных и пространственных свойств и отношений и абстрагирования от всех других свойств. Таким образом, математические объекты реально не существуют. Все они созданы человеческим умом в процессе исторического развития и существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык. Поэтому говорят, что математические объекты – это идеальные объекты, которые описывают реальные объекты.

                Все    математические    объекты    обладают    какими-то    признаками.

Например, квадрат обладает следующими признаками:

-   имеет четыре стороны;

-   все стороны равны;

-   имеет четыре внутренних угла; - все углы прямые и т.д.

Признаки – это все то, в чем объект сходен с другими объектами или отличен от них; все то, благодаря чему объект можно узнать определить, описать.

Каждый объект обладает признаками существенными и несущественными. Существенный признак – такой,  который необходимо принадлежит объекту при всех условиях, без которого данный объект существовать не может. Несущественный признак – это признак, отсутствие которого не влияет на существование объекта. Несущественные признаки могут изменяться, при этом объект остается тем же самым. Но если изменить существенные признаки, то  это будет уже другой объект.  Например, признак «иметь все равные стороны» для квадрата является существенным, а длина стороны – это несущественный признак для указанного объекта. 

Необходимо отметить, что при решения конкретных задач несущественные признаки объекта могут стать существенными для решения данной задачи. Например: 

-   разбить квадраты на две группы:

 

 

 

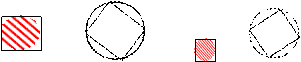
При решении этой задачи ученики будут ориентироваться на такие признаки, как цвет, размер, расположение, которые для понятия «квадрат» являются несущественными.

Чтобы понять, что представляет собой данный математический объект, достаточно знать его существенные признаки. В этом случае говорят, что имеется понятие об этом объекте. Таким образом, понятие – это целостная совокупность суждений о существенных признаках соответствующего объекта. 

Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином (словом, названием). Так, когда говорят о таком понятии, как квадрат, то имеют в виду все геометрические фигуры, которые являются квадратами. Множество всех квадратов составляет объем понятия «квадрат». Таким образом, объем понятия – это множество всех объектов, обозначаемых одним и тем же термином.

Любое понятие, кроме объема, имеет содержание. Содержание понятия – это множество всех существенных признаков объекта, отраженных в этом понятии.

Подход к объему понятия как к множеству дает возможность наглядно представлять отношения между понятиями. Обозначим объем понятия a через А, объем понятия b – В и т.д. Пусть понятия a и b таковы, что объем понятия a является собственным подмножеством объема понятия b, т.е. А В Т.к. А и В – это множества, то отношение между ними можно изобразить на кругах Эйлера:

 

 

 

 

В этом случае говорят, что:

-                      понятие b является родовым для понятия a, понятие a – видовым по отношению к понятию b;

-                      понятие b шире понятия a, понятие a уже понятия b;

-                      понятие b обобщение понятия a, понятие a – частный случай понятия b.

Например, понятие «многоугольник» является родовым по отношению к понятию «треугольник», а понятие «треугольник» - видовым по отношению к понятию «многоугольник». Об этих же понятиях можно сказать, что понятие «многоугольник» шире, чем понятие «треугольник», а понятие «треугольник» уже понятия «многоугольник», либо понятие «многоугольник» есть обобщение понятия «треугольник», а понятие «треугольник» - частный случай понятия «многоугольник».

Существуют понятия, которые не находятся в родовидовых отношениях. Такими, например, являются понятия «треугольник» и «прямоугольник», т.к. их объемы не пересекаются.

Понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию, видовым по отношению к другому. Например, понятие «прямоугольник» - родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник». 

Для одного и того же понятия можно указать несколько родовых понятий, среди них назвать ближайшее.

Итак, всякое понятие имеет определенный объем и содержание. Они взаимосвязаны: чем больше объем понятия, тем меньше его содержание. И наоборот: чем меньше объем, тем больше содержание. Это утверждение справедливо только для понятий, которые находятся в родовидовых отношениях. Так, например, объем понятия «равносторонний треугольник» меньше объема понятия «треугольник», т.к. в объем первого понятия входят не все треугольники, а только равносторонние. Но содержание понятия «равносторонний треугольник» содержит больше свойств, чем содержание понятия «треугольник», потому что равносторонний треугольник обладает не только всеми свойствами треугольника, но и особыми свойствами, которые присущи только равносторонним треугольникам.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Математические понятия и их виды

Понятия выделяют и классифицируют по различным основаниям.

1.                 Понятия делятся на единичные и общие в зависимости от числа объектов в их объеме.

Понятие называется единичным, если в его объем входит только один объект. Например, «наибольшее однозначное число» - это единичное понятие. Если объем понятия содержит более одного объекта, то такое понятие называют общим. Например, понятие «однозначное число» является общим. Объем общего понятия может представлять собой как конечное, так и бесконечное множество.

2.                 Выделяют конкретные и абстрактные понятия. Конкретные понятия характеризуются тем, что в них отображаются признаки объекта или группы объектов. Объекты, входящие в объем конкретных понятий, можно нарисовать, изобразить. Например, понятия «отрезок», «четное число» и т.д. являются конкретными понятиями.

В абстрактных понятиях свойства объектов отвлечены мысленно от самих объектов. Элементы объемов таких понятий нельзя представить (нарисовать, изобразить) в виде конкретных объектов. Примерами абстрактных понятий могут служить понятия: «число», «величина», «множество» и т.д.

3.                 Понятия делятся на сравнимые и несравнимые в зависимости от того, имеются ли в их содержании общие признаки. Сравнимые понятия имеют некоторые общие признаки, несравнимые понятия таких признаков не имеют. Например, понятия «квадрат» и «треугольник» сравнимы, т.к. у них есть общий признак – быть многоугольником. Понятия «квадрат» и «уравнение» - несравнимые, у них нет ни одного общего признака.

Сравнимые понятия делятся на совместимые и несовместимые. Объемы совместимых понятий имеют хотя бы один общий элемент. В объемах несовместимых понятий общих элементов нет. Например, понятия «четное число» и «число, кратное 2» совместимы, причем объемы этих понятий полностью совпадают. В этом случае говорят, что понятия находятся в отношении тождества. Объемы совместимых понятий могут так же находиться в отношении пересечения и включения.

Понятия «квадрат» и «треугольник» являются несовместимыми, т.к. объемы этих понятий не имеют ни одного общего элемента.

Таким образом, можно составить следующую схему деления понятий: понятия

 

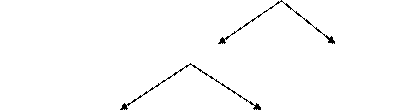
           совместимые             несовместимые

Объемы совместимых понятий могут находиться в трех видах отношений.

Отношение тождества. Объемы таких понятий совпадают. Например, объемы понятий «прямоугольник с равными сторонами» и «ромб с прямыми углами» находятся в отношении тождества.

Отношение пересечения. Объемы таких понятий имеют некоторые общие элементы. Например, объемы понятий «четное число» и «число кратное трем» находятся в отношении пересечения, т.к. есть числа 6, 12, 18, которые кратны и двум и трем одновременно.

Отношение включения. В этом случае объем одного понятия является подмножеством другого. Примерами понятий, объемы которых находятся в отношении включения, могут служить понятия «квадрат» и

«прямоугольник».

 

 

3. Определение математических понятий. Требования к определению понятий.

Одним из действий изучения математического объекта для получения понятия о нем является действие определение. Определить понятие - значит указать способ, с помощью которого можно отделить объекты или отношения, охватываемые данным понятием, от других объектов или отношений.   

Определяя понятие,  приходится совершать некоторую логическую операцию, в результате которой формулируется предложение, раскрывающее содержание понятия. Сами предложения при этом называются определениями. Таким образом, определение – это предложение, с помощью которого раскрывается содержание понятия или устанавливается значение термина.

В содержание понятия о каком-либо  математическом объекте входят различные существенные признаки этого объекта. Однако, для того чтобы распознать объект, установить, принадлежит он к данному понятию или нет, достаточно проверить наличие у него лишь некоторых существенных признаков. Указание этих существенных признаков объекта, которые достаточны для распознавания этого объекта, понятия, и называют определением понятия.

Определить понятие – это значит выбрать из его существенных признаков такие и столько, чтобы каждое из них было необходимо, а все вместе достаточны для того, чтобы отличить изучаемый объекта от других. 

Выполняется действие определения различными путями, и результат его выполнения фиксируется в различного вида определениях.

Различают вербальные (словесные)  и невербальные определения.  

Невербальное     определение         –        это определение понятия путем непосредственной демонстрации объектов, охватываемых этим понятием, или приведение контекста, в котором содержится то или иное понятие. 

Невербальные    определения        используются      на      начальном этапе изучения объектов или отношений. Поэтому учитель начальных классов должен быть знаком с ними особенно хорошо. 

Примерами таких определений являются остенсивные и контекстуальные определения. 

Остенсивные (от лат. ostendere – показывать) определения – это такие

определения, которые устанавливают значение терминов путем демонстрации объектов, которые этим термином определяются. С использование такого определения в начальной школе вводится понятие «числовое выражение», «числовое равенство», «угол» и т.д. Покажем это на примере числового выражения.

В учебнике по математике для 2 класса УМК «Школа России» (авт.

М.И. Моро, М.А. Бантова,  Г.В.Бельтюкова, С.И.Волкова, С.В. Степанова) предлагается задание:  

«Прочитай записи:

9 + 7               30 + 6 + 1              18 – (4 + 6)

23 – 3             15 – 7 + 3              25 – (15 – 10) 

Это числовые выражения, или, короче, выражения».

В других современных учебниках математики содержатся аналогичные записи, меняются только математические объекты, в зависимости от того, в каком классе (1-ом или 2-ом) дети знакомятся с этим понятием, при этом способ знакомства остается одним и тем же – путем показа. Важно понимать, что если учитель ограничится только показом, то это не даст ученикам четкого представления о том, в чем же заключается содержание данного понятия. Необходимо провести аналитическую работу, в результате которой дети выяснят: чем похожи и чем отличаются числовые выражения, т.е.сами  выделят и назовут существенные и несущественные признаки  понятия «числовое выражение»

Контекстуальные определения – это определения, в которых содержание понятия  раскрывается через некоторый контекст. Например, понятие деление натуральных чисел в учебнике математики для начальной школы Истоминой Н.Б. (УМК «Гармония»)  вводится контекстуально. Смысл действия деления раскрывается с помощью рисунка и специально сконструированного текста: «Расскажи, как разделили конфеты. Объясни, что обозначает каждое число в равенствах, записанных под рисунком. Для записи деления в математике используют знак:

12 : 6 = 2        12 : 2 = 6

12 : 3 = 4        12 : 4 = 3».

Чтобы ученики поняли, что представляет собой деление чисел, необходимо увидеть в приведенном рисунке разбиение совокупности на части и две задачи, которые связаны с этим разбиением (деление на равные части и деление по содержанию).            

По мере накопления запаса знаний происходит накопление понятий, развивается язык и способность к обобщению. Все это дает возможность определять неизвестные понятия через известные. Так появляются вербальные определения.  Во всяком таком определении выделяются определяемое и определяющее понятия. Например, в определении «Квадратом называется прямоугольник, у которого все стороны равны»  понятие «квадрат» является определяемым, а понятие «прямоугольник, у которого все стороны равны» - определяющим.

Рассмотрим некоторые способы вербальных определений.

                1)      Определение понятий через род и видовое отличие. 

Этот способ определения является наиболее распространенным. Логическая структура определения через род и видовое отличие проста, четко выражена и поэтому доступна учащимся уже в начальной школе. Такие определения часто представляют в виде схемы: вид = род + видовое отличие.

Например: «Прямоугольник – это четырехугольник, у которого все углы прямые».

Вид – прямоугольник.

Род – четырехугольник.

Видовые отличия: все углы прямые

Операции, раскрывающие действие определения объектов, в этом случае будут следующими: выбирается ближайший родовой объект, затем на этот объект накладываются как бы ограничения, видовые характеристики (отличия). На основе видовых характеристик вводится новый объект, но с меньшим объемом, чем родовой, т.к. у него больше свойств. Вот этому объекту с большим числом свойств и меньшим объемом присваивается новое звание (термин).

2)               Генетическое определение понятий.

Генетические (от слова генезис – происхождение), или конструктивные, определения являются частным случаем определений через род и видовое отличие. В таких определениях видовое отличие указывает на происхождение определяемого объекта или на способ его образования. 

Рассмотрим, например, определение треугольника: «Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков». В этом определении указано родовое понятие для треугольника – фигура, а в качестве видового отличия указан способ построения такой фигуры, которая является треугольником: нужно взять три точки, не лежащие на одной прямой, и соединить каждую их пару отрезком. 

3)               Рекурсивные определения. 

В таких определениях указываются некоторые основные элементы из объема понятия и даются правила, позволяющие получить новые элементы из уже имеющихся. Например, определение арифметической прогрессии: «Арифметической прогрессией называется последовательность, в которой каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом». 

В математике существуют понятия, которые логически не определяются. Такие понятия называют основными или первичными.

Примерами таких понятий являются: точка, прямая, множество, величина.

К определению понятий выдвигается ряд требований

1.                  Определение должно содержать указание на ближайшее родовое понятие. Как бы ни было построено определение математического понятия, в нем должно быть указано ближайшее родовое понятие к определяемому понятию. 

Нарушение этого требование приводит к различного рода ошибкам. Например,  иногда учащиеся, формулируя определение понятия, не указывают родовое понятие. На вопрос, что такое  прямоугольник, они отвечают: «Прямоугольник – это когда все углы прямые». Такая небрежность в формулировке определений недопустима, т.к., что означает «это», можно только догадываться.

Другой тип ошибок связан с тем, что в определении указывается не ближайшее родовое понятие, а более широкое. Пример такого определения: «Квадрат – это четырехугольник, у которого все стороны равны». В этом определении указано не ближайшее для квадрата родовое понятие – «прямоугольник», а более широкое – «четырехугольник». И тем самым это определение становится неверным, т.к. четырехугольником,  у которого все стороны равны, может быть не только квадрат, но и ромб.

2.                  Определения не должны содержать «порочного круга». Считают, что определение содержит «порочный круг», если в его определяющей части содержится определяемый термин. Например, в определении «Решением уравнения называется число, которое является решением этого уравнения» содержится «порочный круг»- понятие «решения уравнения» определяется через «решение уравнения». Может случиться, что «порочный круг» содержится в цепочке определений. Например, «Умножением чисел называется действие, при помощи которого находят их произведение» и «Произведением чисел называется результат их умножения». В этом примере умножение определяется через понятие произведения, а произведение – через умножение. Определения образовали «порочный круг». 

3.                  Определение не должно быть тавтологией, т.е. повторять в иной словесной форме ранее сказанное. Сущность такой ошибки в том, что понятие определяется через само себя.  Например, «Сложением называется действие, при котором числа складываются». Здесь сложение определено через понятие «складывание», что одно и то же.

4.                  Определение должно быть достаточным. Это означает, что в определении должны быть указаны все признаки, позволяющие однозначно выделить объекты определяемого понятия. Если же это требование нарушается, то под определение можно подвести не только объекты определяемого понятия, но и другие объекты. Например, «Медианой треугольника называется отрезок, делящий его сторону пополам». Очевидно, что в этом определении указано недостаточное число признаков для медианы. Поэтому под это определение подходят не только медиана треугольника, но средняя линия треугольника, и вообще любой отрезок, делящий сторону треугольника пополам.

5.                  Определение не должно быть избыточным. Это значит, что в определении не должно быть указано лишних признаков, вытекающих из других, уже указанных в определении. Например, «Прямоугольником называется четырехугольник, у которого противоположные стороны равны и углы прямые». Свойство «иметь противоположные равные стороны» вытекает из свойства «иметь прямые углы». Значит, данное определение прямоугольника избыточно.

Получение определения понятия – это не конец усвоения понятия, а лишь первый шаг на этом пути. Следующий важный шаг состоит в том, чтобы научить учащихся ориентироваться на содержание определения при выполнении различных действий с объектами. Другими словами, надо не только задать точку зрения на вещи, но и добиться того, чтобы эта точка зрения была принята и реально использовалась учащимися. Если это не обеспечено, то в одних случаях определение может остаться в стороне: ученик будет опираться на другие свойства, которые он сам выделил в объекте.  В других случаях ученики могут пользоваться только частью указанных свойств; в третьих  –  могут добавить к указанным в определении свои, что также приводит к ошибкам.

 

 

 

 

 

 

 

 

 

 

 

 

 

4.     Виды          действий,   используемых    при   формировании математических понятий.  

Основная цель изучения понятий – это правильное усвоение школьниками содержания понятий и использование последних в своей учебной деятельности. В состав любой деятельности  входят действия и операции. Поэтому существенные свойства понятий можно раскрыть учащимся через выполнение конкретных действий с понятиями. При этом термином «действие» обозначается отдельный акт учебной деятельности учащихся, подчиненный достижению определенной цели. При выборе действий, которые должны выполняться с понятиями, необходимо учитывать следующее: какое понятие изучается, какая цель ставится относительно изучения данного понятия, какими предварительными умениями овладели ученики и т.д. Например, при формировании понятия «однозначное число» ставится цель научить учащихся правильно читать и записывать однозначные числа, знать порядок следования этих чисел в натуральном ряду, знать и уметь записывать состав однозначных чисел из отдельных единиц. 

Если рассматривать понятие «многозначное число», то с ним ученики, кроме отмеченных действий относительно понятия «однозначное число», должны уметь выполнять и другие действия. Например, представлять многозначное число в виде суммы разрядных слагаемых, находить в нем число единиц, десятков, сотен и т.д.

При значительном разнообразии действий с понятиями из их числа можно выделить некоторые общие действия.

1. Распознавание предметов, входящих в объем данного понятия.

Действие распознавания наиболее часто используется в начальной школе. Цель этого действия состоит в том, чтобы правильно выделить (узнать) необходимый математический объект в данной совокупности объектов. Распознавание предметов всегда осуществляется по существенным признакам. Поэтому важнейшая методическая задача учителя заключается в том, чтобы правильно сориентировать учащихся на такие признаки. Ее решение в начальных классах существенно осложняется, т.к. здесь в основном используются такие приемы раскрытия содержания понятий, в которых явно существенные признаки не указываются (например, прием показа). Приведем примеры задач на распознавание.

Задача 1. Назови все лучи и углы на рисунке. Выпиши сначала название прямых углов, потом тупых и затем острых углов (Моя математика. 2 класс, ч.3. УМК «Школа 2100», авт. Т.Е. Демидова, С.А. Козлова, А.П.

Тонких ).

                                                С         Д

       В                                      

                                                                                 М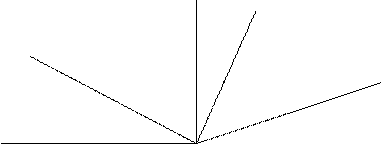

 

                                                                                                                       А                                   О  

Задача 2. Назови все прямоугольники. Назови фигуру, которая занимает больше всего места на листе. (Моя математика. 2 класс, ч.2. УМК «Школа 2100», авт. Т.Е. Демидова, С.А. Козлова, А.П. Тонких).

А              В                           С                   Д

 

М             К                            N                  P 

Задача 3. Выпиши в один столбик равенства,  а в другой – неравенства (Математика. 1 класс, ч.1. УМК «Школа России», авт. М.И. Моро, М.А.

Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова).

3 – 1 = 2    5 – 1 < 5      3 + 1 > 2.

Решение задач на распознавание принадлежности объекта объему данного понятия основывается, как правило, на определении этого понятия через род и видовое отличие. Если определение содержит одно видовое свойство, то распознавание проводится по следующему плану.

1)                Проверяем, принадлежит ли объект объему родового понятия. Если окажется, что не принадлежит, то проверку прекращаем и делаем вывод, что объект не принадлежит объему понятия.

2)                Если объект принадлежит объему родового понятия, то продолжаем проверку и выясняем, обладает ли объект видовым отличием. 

3)                Если объект обладает этим свойством, то делаем вывод о его принадлежности к объему данного понятия.

4)                Если объект не обладает этим свойством, то делаем вывод о том, что объект не принадлежит объему данного понятия.

Приведем пример использования описанного плана. 

В учебнике математики для 2 класса (УМК «Школа России, 2 класс, ч.1, авт. М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В.

Степанова) предлагается задание: 

«Найди среди следующих записей уравнения, выпиши их и реши.

30 + х > 40           45 – 5 = 40            60 + х = 90

80 – х                    38 – 8 < 50            х – 8 = 10».

Чуть раньше дети познакомились с определением уравнения: «Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Неизвестное число обозначают маленькими латинскими буквами, например х (икс)».

Родовым понятием в этом определении является понятие равенство, а видовым отличием – содержать неизвестное число, обозначенное буквой, которое нужно найти. Используя описанный выше алгоритм, рассуждения можно провести следующим образом.

Рассмотрим все записи, например, первой строки.

Запись 1 не является равенством. Следовательно, она не является уравнением.

Запись 2 – это равенство, но в нем нет неизвестного числа, следовательно, она не является уравнением.

Запись 3 – это равенство, которое содержит неизвестное число, обозначенное буквой х. Следовательно, это уравнение.

Аналогично рассматриваются все записи второй строки предлагаемого задания.

Для того, чтобы облегчить выполнение действия распознавания учащимися, можно использовать такой прием, как работа с таблицей. Покажем это на примере такого понятия, как квадрат.

Учащимся предлагается ряд фигур, среди которых нужно найти квадраты.

1

2

Воспользуемся определением, которое предлагается в начальной школе: «Квадрат – прямоугольник, у которого все стороны равны». Родовым понятием является понятие прямоугольник, а видовым отличием – все стороны равны. В вертикальном столбце таблицы отметим те признаки, по которым и будем распознавать квадрат среди других фигур. По горизонтали напишем номера фигур. На пересечении будем ставить знак «+», если фигура обладает указанным свойством, и знак «–», если свойством не обладает. На основании полученных данных заполняем последнюю строку, в которой отмечаем, является ли фигура квадратом или нет.

	1	2	3	4	5	6
прямоугольник	+	+	+	–	–	–
все стороны равны	–	+	+	+	–	–
квадрат	–	+	+	–	–	–

С учащимися полезно обсудить вопрос о том, нужно ли проверять второе свойство, если не выполняется первое. 

Так решаются задачи на распознавание, если в определении имеется одно видовое свойство. Если же видовое отличие состоит из нескольких свойств, которые находятся в конъюнктивной связи (связаны союзом «и»), то объект принадлежит объему данного понятия при условии, что он обладает всеми свойствами, включенными в видовое отличие. Если связь между свойствами видового отличия дизъюнктивная (с помощью союза «или»), то объект принадлежит объему данного понятия, если обладает хотя бы одним из свойств.

Умение решать задачи на распознавание является показателем уровня сформированности понятия. В то же время, как показывает практика обучения младших школьников, они испытывают затруднения при решении задач на распознавание. Анализ ошибок, допускаемых школьниками при решении задач такого вида, позволяет сделать вывод, что причины  ошибок могут быть следующими:

а) учащиеся плохо понимают, как устроено определение и, как следствие, не выделяют в его формулировке родового понятия и видового отличия;

б) не понимают, что в определение понятия включаются только

существенные свойства определяемого объекта.

 Часто причина ошибок при решении задач на распознавание связана с тем, что понятия определяются остенсивно или контекстуально. В этом случае школьникам предъявляется объект и вводится термин (остенсивный способ определения) или предлагается специально сконструированный текст, в котором необходимо увидеть существенные свойства понятия

(контекстуальный способ определения). 

Чтобы предупредить такие ошибки, необходимо при введении определения того или иного понятия не только обращать внимание на его структуру, но и выполнять соответствующие упражнения.

Так, например, понятие числового выражения в начальной школе, как уже отмечалось, вводится остенсивно. Можно предложить решить следующую задачу на распознавание:

«Даны записи:

.8 + 3                   14 – 4 +6            14 + 2 > 14 – 2

20 – 1 – 10          13 – (5 + 2)         14 – 5

8 < 16 – 7            12 – 6 = 5 + 1     8 + 4 – 1

Миша утверждает, что все эти записи можно назвать числовыми выражениями. Прав ли Миша? Ответ обоснуй».

2. Действие подведения под понятие.

Действие подведения под понятие состоит из следующих компонентов: 

а) указание системы необходимых и достаточных свойств данного класса объектов.  При этом предполагается, что учащиеся уже знают особенности этих свойств и отличают их от других: существенные – несущественные; необходимые – достаточные; необходимые и одновременно достаточные. Последние обычно указываются в определениях понятий;

б) установление, обладает ли данный объект выделенными свойствами или не обладает. Правильное выполнение этой части действия подведения под понятие предполагает, что учащийся уже усвоил способы опознания проверяемых свойств. Так, если надо проверить, являются ли линии прямыми, то ученик должен уметь воспользоваться линейкой. Но практические   умения помогут ему только тогда, когда распознаваемый объект представлен в виде чертежа, рисунка, реального предмета. Если же объект задан через описание, то ученик должен уметь анализировать условие задачи, выделять в нем информацию о проверяемом свойстве;

в) заключение о принадлежности объекта данному понятию.

Для того, чтобы правильно происходило подведение объекта под то 6или иное понятие, учащимся нужно, во-первых, научиться выделять понятие, под которое требуется подвести данный объект. Во-вторых, надо установить, при каких условиях данный объект может относиться к данному понятию.

Примеры заданий на формирование действия подведение под понятие:

1)                докажи, что указанная фигура является (не является) прямоугольником;

2)                обоснуй, почему записи 3 + х; 18 : 2 = 9 не являются уравнениями;

3)                докажи, что все следующие записи можно назвать числовыми выражениями: 

82 – 7  6 + 19             65 – 16 + 24 : 3            (87 – 39) + (65 – 28) 7  9 – 8                        72 : 8                             38 + 26

Как может рассуждать ученик при выполнении первого задания? 

Действия распознавания и подведения под понятие имеют много общего: и в том, и в другом случае учащимся необходимо знать существенные свойства рассматриваемого понятия. Различие заключается в том, что при решении задач на распознавание ученики должны выяснять, чем отличаются предлагаемые объекты, а при рассмотрении действия подведения под понятие выделяют общее для всех объектов, принадлежащих одному понятию.

3. Получение следствий.

Цель этого действия состоит в том, чтобы с разных сторон рассмотреть предмет, выбранный из объема данного понятия, изучить его в плане разных понятий. Выполнение такого действия формирует умение рассматривать один и тот же объект с разных сторон, что очень важно для развития учащихся. 

Например, предлагается задание: 

«Что можно рассказать о следующей записи: 3 + 5= 8?» Возможны следующие варианты ответов:

-   это числовое равенство;

-   это верное числовое равенство;

-   первое слагаемое – 3, второе слагаемое – 5, сумма равна 8;

-   первое слагаемое меньше второго на 2;

-   слагаемые – нечетные числа, а сумма – четное число;

-   все числа, которые используются в равенстве, однозначные;

-   сумма больше первого слагаемого на 5, а второго слагаемого – на 3.

Таким образом, выполняя предложенное задание, ученики уточняют не только понятие числового равенства, но и такие понятия, как слагаемое, сумма, четное и нечетное число, однозначное число, понятия «больше на…», «меньше на…».

Выведение следствий фактически  противоположно действию подведения под понятие. При подведении под понятие надо по системе определенных свойств решить вопрос о принадлежности данного предмета к классу объектов, зафиксированных в понятии. При выведении следствий с самого начала известно, что объект принадлежит данному классу. Задача заключается в том, чтобы из этого факта принадлежности получить следствия, сделать выводы о свойствах этого объекта. Таким образом, в первом случае совершается переход от свойств объекта к принадлежности к классу, а во втором  –  наоборот.

4.   Сравнение понятий по содержанию и по объему.

Целью такого действия является выявление сходного и различного в рассматриваемых понятиях для более четкого усвоения отличительных признаков объектов. Делается это путем постановки соответствующих вопросов. Например, какой общий признак у всех уравнений? Сохранится ли уравнение, если вместо знака равенства поставить знак неравенства? Почему? Какой признак надо убрать у квадрата, чтобы он стал не прямоугольником? Чем похожи все числовые равенства? Чем они отличаются? Чем отличаются понятия «числовое равенство» и «числовое выражение»?

Необходимо отметить, что сравнение должно происходить на основе существенных свойств. Действие сравнения помогает учащимся понять место усваиваемого понятия среди других. 

Ценность рассмотренных действий на получение следствий и сравнение состоит в том, что их выполнение содействует усвоению понятий во взаимосвязи, в некоторой системе.

5.   Классификация.

Действие классификации более сложное, чем выше рассмотренные. Классификация дополнительно требует понимания родовидовых отношений и предполагает наличие понятий о роде и виде.  Классификация позволяет, с одной стороны, включать изучаемое понятие в систему других, ранее изученных, с другой  –  увидеть подклассы объектов, входящих в объем изучаемого понятия. Так, четырехугольник может быть рассмотрен и как один из видов многоугольников и как родовое понятие, включающее целое множество различных видов. Классификация включает ряд действий и требует выполнения ряда условий. 

В состав этого действия входят такие операции, как определение признаков объектов; выбор основания для классификации; деление по этому основанию всего множества объектов, входящих в объем данного понятия; построение иерархической классификационной системы. Прежде всего учащиеся должны научиться выбирать основание классификации и сохранять его до конца работы, пока не исчерпают весь объем понятия. В качестве основания классификации берутся отличительные существенные признаки понятия. Напомним, что существенные признаки – это те, которыми данный класс объектов отличается от других классов, например четырехугольники от других геометрических фигур. А отличительные признаки – те, которыми различаются разные объекты друг от друга внутри этого класса, например квадраты от всех остальных четырехугольников.

Приведем пример выполнения действия классификации  при работе с таким понятием как «числовое выражение».

«Догадайся, по какому признаку записаны выражения в каждом столбике?

29 – 8 + 24               72 : 9  3                  84 – 9  8

32 + 9 – 7 + 14         48 : 6 7 : 8            54 + 6  3 – 72

                64 – 7 + 16 – 8        27 : 3     2 : 6     9        8 + 7  8 + 63 :9»

 

Рассмотрим ниже задания, иллюстрирующие выше названные действия, на примере изучения понятия «числовое выражение». 

Вначале выясним, как вводится это понятие в некоторых учебниках по математике для начальной школы.

1. Математика 2 класс, ч.1. (УМК «Школа России», авт. М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова).

В указанной программе понятие «числовое выражение» вводится остенсивно (путем показа). Кроме этого,  дается контекст, в котором раскрывается понятие «значение числового выражения»:

«Прочитай записи.

9 +7        30 + 6 + 1             18 – (4 + 6)

23 – 3      15 – 7 +3              25 – (15 – 10)

Это числовые выражения, или короче, выражения.

Если в выражении выполнить указанные действия, то найдем значение выражения».

2. Моя математика 1 класс, ч.1. (УМК «Школа 2100», авт. Т.Е.

Демидова, С.А. Козлова, А.П. Тонких).

В этом учебнике понятие «числовое выражение» вводится только путем показа объектов, входящих в объем данного понятия, без какого-либо текста. Одновременно с этим понятием вводятся также понятия «значение числового выражения» и «числовое равенство».

Учащимся предлагается обратить внимание на следующие записи:

                   1 + 2                                    2 _– 1     – числовые выражения

 

            3                      1        – значения выражений

1 +2 = 3            2 – 1 = 1 – числовые равенства

2. Математика 1 класс (УМК «Гармония» авт. Н.Б. Истомина)

С понятием «числовое выражение» знакомятся, как и в рассмотренных выше учебниках, путем показа. Это понятие вводится одновременно с рассмотрением конкретного смысла действия сложения и понятием «числовое равенство». Так детям предлагается задание: «Расскажи, что делают Маша и Миша.

Действия Маши и Миши можно записать числовыми выражениями.

3 + 2      5 + 4     3 + 1     3 + 4

2 + 3     4 + 5      1 + 3     4 + 3

Выражения со знаком  «+» называют сумма, а числа, которые складывают – слагаемые.

Результат сложения называют значением суммы.

Запись 4 + 5= 9 называют числовым равенством.

Таким образом,  в каждом из рассматриваемых учебников понятие «числовое выражение» вводится остенсивно. Различаются подходы только временем знакомства (1 или 2 класс) и объектами, которые предлагаются для рассмотрения.

Приведем   примеры     заданий      из      рассмотренных    учебников, направленных на формирование понятия «числовое выражение».

Необходимо отметить, что заданий на распознавание числовых выражений  в указанных учебниках нет, поэтому составим такие задания сами. В качестве объектов, среди которых дети будут распознавать числовые выражения, выберем те, с которыми часто смешивают это понятие, это  – числовые равенства, числовые неравенства. Если такое задание предлагается в 4  классе, то можно добавить выражения с переменной. Например, для учащихся 3 класса предложим такое задание: 

– Среди следующих записей найти числовые выражения:

13 + 8; 74 – 12 = 16; 8  4 + 42 : 7;  37 + 19 > 9   (46 – 16) : 5

9; 

35 < 12  3; 8 + 4 = 24 : 2.

Работу с этим заданием можно продолжить, выполнив следующие действия: чтение найденных выражений и нахождение значений этих выражений. Причем полезно предложить прочитать выражения разными способами. Например, выражение 13+8 можно прочитать следующим образом:

–                    тринадцать плюс восемь; 

–                    к тринадцати прибавить восемь;

–                    первое слагаемое – 13, второе – 8; – тринадцать увеличить на восемь.

Аналогично можно прочитать и сложное выражение. Покажем это на примере   8  4 + 42 : 7:

–                    к произведению восьми и четырех прибавить частное сорока двух и семи;

–                    первое слагаемое – произведение восьми и четырех, второе – частное сорока двух и семи.

Задания, в процессе выполнения которых формируется умение читать выражения, могут звучать по-разному. Например:

а) прочитай выражения разными способами;

б) прочитай выражения, используя только название компонентов

действий;

в) прочитай выражения, используя отношения «больше на…» («меньше на…», «больше в…», «меньше в…»).

Приведем другие примеры тех действий, которые направлены на формирование понятия «числовое выражение». К каждому действию подберем соответствующие задания, которые могут звучать по-разному.

Наиболее распространенным является действие, связанное с формированием умения находить значение выражений.  Примеры заданий.

2+1+3

 

4+1+1+1

3+1+1

❶. Ветер разбросал Катины записи. Помоги ей навести порядок, подбери к каждому выражению его значение.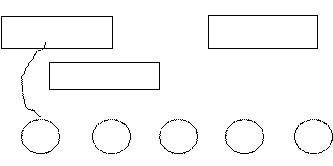

❷. Запиши выражения и найди их значения. а) Из числа 16 вычесть разность чисел 9 и 7.

б) К числу 10 прибавить разность чисел 7 и 5.

❸. Вычисли удобным способом.

30 + 7 + 40 +3      20 + 6 +50 + 4

❹. Вспомни правило о порядке выполнения действий и вычисли значения выражения.

100 – (60 + 24)        60 – (80 – 37)         9 + 7 – 8

(70 + 25) – 90          70 – (50 – 6)           9 – 4 + 7

❺. Расставь порядок действий в выражениях и прочитай их.

11 – 6 + 5           13 – 7 – 4           (15 – 6) + 8 11 – (6 + 5)         13 – (7 – 4)         15 – (6 + 8)

Найди и сравни значения выражений.

❻. Установи порядок действий в выражениях и найди их значения.

28 : 4 ∙ 6 + (67 – 66) ∙ 5                          (8 – 0) : 8 ∙ 15

(34 + 6 ∙ 6) – 9 ∙ 0                                   (3 ∙ 4 – 6 ∙ 2) : 20 ∙ 7

 ❼. В каждом столбике найди значение второго выражения, используя значение первого.

      9 ∙ 7 = 63           7 ∙ 10 = 70           15 ∙ 4 = 60

      9 ∙ 8 =               7 ∙ 9 =                    15 ∙ 5 =

Как видно из приведенных примеров, умение записывать выражения формируется одновременно с умением выполнять чтение  и находить значение выражений.

Действие сравнения. Примеры заданий.

❶. Чем похожи выражения и чем они отличаются?

12 + 6;    12 + (12 + 6);   (18 – 9) + 3;   100 – 45;    35 + 2 + 48 + 5; 44 – (20 – 6);    65 – 8 + 30.

❷. Сравни две записи. Чем они похожи и чем отличаются? Как называется каждая запись?

а) 8 + 7  и  8 + a

б) 8 + 7  и  8 + 7 = 15

❸. Сравни выражения, поставив знак «больше», «меньше», «равно». 5 – 2 🌕 1 + 4       5 + 3 🌕 3 + 5       6 – 2 🌕 6 – 3

❹. Сравни выражения в каждом столбике и объясни, как получено каждое следующее из предыдущего.

7 + 8 + 3 + 2

7 + 3 + 8 + 2

(7 + 3) + (8 + 2) 10 +10

Вычисли значения выражений и сравни их.

❺. Сравни выражения, не вычисляя их значений.

36 – 4 и 36 – 6;                   88 – 7 и 98 – 7

7   + 32 и 32 + 7                    79 – 6 и 97 – 7

❻. Рассмотри суммы и, не вычисляя их значений, определи, какая из них больше.

8   + 7 +15 + 65   и   7 + 65 + 20 + 8

❼. Сравни выражения в каждом столбике. Найди значение первого из них и вычисли значения остальных самым легким способом.

  8 + 57      97 – 27

18 + 57      97 – 30

28 + 57      97 – 33

38 + 57     97 – 36

 ❽. Назови в каждом ряду разность с наибольшим и наименьшим значением.

а) 15 – 7; 15 – 8; 15 – 9; 15 – 6;

б) 11 – 9; 12 – 9; 13 – 9; 14 – 9; 15 – 9.

Надо ли искать значения выражений, чтобы выполнить это задание?

❾. Чем похожи эти выражения?

       20 – 3     80 – 3     30 – 3

       50 – 4     70 – 4     60 – 4

       60 – 2     40 – 2     50 – 2

Найди значение выражений. Подчеркни цифры, обозначающие десятки в уменьшаемом и в значении разности. Что ты заметил?  

❿. В чем сходство и различие выражений, записанных слева и справа?

Прочитай их по-разному. Вычисли значения выражений и сравни их.

9 ∙ 8  … 9 + 8

8 ∙ 7 … 8 + 7

6 ∙ 4 … 6 + 4

5 ∙ 3 … 5 + 3

Составление выражений. Примеры заданий.

I. Составление выражений по рисунку, образцу или инструкции.

❶. Катя, Петя и Вова перепутали свои рисунки и записи. Подбери к каждому рисунку нужное выражение и его значение. 

К.                                             П.                                               В.

1+2			1+1		2+1		2-1
2		1				3

 

3+4

 

2+5

 

5+2

❷. Какие из этих выражений описывают рисунок Вовы? 

Расскажи, какие еще выражения можно составить по данным рисункам.

❸.Используя числа 10, 9, 1, знаки «+», «–» и скобки, составь различные выражения и найди их значения.

❹.Составь выражение и найди его значение: к разности наибольшего двузначного числа и числа 77 прибавить наименьшее двузначное число.

❺. Составь два выражения со скобками так, чтобы значение каждого выражения было равно 15.

❻. Используя таблицу, составь выражения и вычисли их значения.

Уменьшаемое	50	50	50	60	70	80
Вычитаемое	3	9	10	8	7	6

❼.Придумай выражения, в которых:

а) уменьшаемое состоит из 3 дес. 8 ед.;

б) вычитаемое состоит из 5 дес. 3 ед.;

в) первое слагаемое состоит из 2 дес. 9 ед.;

г) второе слагаемое состоит из 3 дес.

Найди значения этих выражений.

I I. Составление задач по выражению.

❶. В мастерской было на ремонте 6 машин. Через день на ремонт поставили еще 3 машины, а 2 машины вернули после ремонта. Сколько машин стало в мастерской?

1) Выбери выражение, которое составлено по этой задаче, и реши задачу.

6 – 3 + 2      6 + 3 + 2      6 + 3 – 2     6 – 3 – 2

2) Изменяй условие задачи так, чтобы для решения подходили другие из написанных выражений. Реши новые задачи.

❷. Составь задачу по выражению и реши ее.

30 + (30 – 8)

❸. 1) В парке посадили 30 липок, а дубков на 10 больше. Сколько дубков посадили?

2) В парке посадили 30 липок, а дубков на 10 больше. Сколько всего липок и дубков посадили?

Рассмотри выражения и объясни, к какой задаче относится каждое из них:

30 + (30 + 10);        30 + 10.

❹. Для костра Страшила принес 5 веток, Элли 7 веток, а Железный

Дровосек в 4 раза больше, чем Страшила и Элли вместе. Сколько веток принес Железный  Дровосек?

1)  Составь выражение к этой задаче.

2)  Задай вопрос к задаче так, чтобы ее решением было выражение:  (7 + 5) ∙ 4 + (7 + 5)

3)  Придумай задачу по выражению: 5 + 7 ∙ 4.

Классификация. Примеры заданий.

❶. Разбей выражения на группы и найди их значения.

4 – 2; 5 – 1 – 1; 4 – 1 – 1; 5 – 2.

❷. Какое выражение здесь «лишнее»?

1)    6 – 0; 10 – 4; 3 + 3; 8 – 2; 9 – 5

2)    8 – 6, 6 + 3, 2 + 6, 8 – 2 

❸. Выбери все выражения, значения которых равны 18.

26 – 6 – 2        24 – (13 – 9)       15 + (11 – 8)

❹. Вычисли. Разбей выражения на группы.

8   + 3 – 5        15 – 7 – 2       10 – 2 + 5

9   – 4 + 8          3 + 4 + 6       14 – 4 – 4

Составь задачи по первому и последнему выражению.

❺. Разбей выражения на группы:

4 + 4 + 4;    3 + 9;   6 + 6;   2 + 4 + 9;   1 + 8 + 3;   10 +4;   5 + 5 + 5.

Сколько способов разбиения ты нашел?

❻. Страшила записал некоторые числа в виде суммы. На какие группы можно разбить эти выражения? Какие числа записаны в виде суммы разрядных слагаемых?

259 + 1              600 + 9                 400 + 10

340 + 1              700 + 20 + 2         200 + 52.

❼. Какое выражение «лишнее» в каждом столбике?

а) (8 + 6) ∙ 4                                             б) 2 ∙ (37 +240     4 ∙ (8 + 6)                                                 (37 + 24) ∙ 2

    (8 + 6) + (8 + 6) + (8 + 6) +(8 + 6)           2 ∙ 37 + 24

    4 ∙ 8 + 8                                                    37 ∙ 2 + 24 ∙ 2

    8 ∙ 4 + 6 ∙ 4                                               (37 + 24) + (37 + 24)

Тождественное преобразование выражений.

Два выражения называются тождественно равными, если они имеют одинаковые значения. Замена одного выражения другим, тождественно равным, называется тождественным преобразованием выражения. Тождественное преобразование выражения может быть основано на свойствах арифметических действий, конкретном смысле арифметических действий, правилах действий. Приведем примеры соответствующих заданий.

❶. Вычисли удобным способом.

2 + 3 + 8 + 7      19 – 1 – 8     (7 + 4) – 3

14 – (4 + 5)        8 + (2 + 5)     4 + 3 + 2 + 6

❷. Витя записал два столбика выражений. Для каждого выражения левого столбика найди выражение правого столбика с таким же значением и найди это значение.

140 ∙ 2                     (100 + 2) ∙ 3

480 : 4                     (600 + 20) : 2 102 ∙ 3                     (100 + 40) ∙ 2

620 : 2                     (400 + 80) : 4

306 : 3                     (300 + 6) : 3

❸. Как Томми быстро найти значения данных выражений?

128 ∙ 2 + 172 ∙ 2             195 ∙ 5 – 5 ∙ 195            98 ∙ 4 – 89 ∙ 4

560 : (201 – 197) ∙ 0       85 ∙ 7 + 85 ∙ 3                92 ∙ 9 – 92 ∙ 8

189 : 9 + 711 : 9            97 + 97 ∙ 9                     728 – 69 – 69

❹. Продолжи запись:

18 ∙ 20 = 18 ∙ (2 ∙ 10) = 

18 ∙ 12 = 18 ∙ (2 + 10) = 

Определение закономерности, по которой составлены выражения.

Примеры заданий.

❶. Составь пропущенные выражения и найди их значения.

11  – 9 + 8               15 – (11 – 5)

12  – 8 + 7               15 – (12 – 5)

      …                              …

15 – 5 + 4                15 – (15 – 5)

❷. Запиши еще по 2 выражения в каждом столбике и выполни вычисления.

48 + 12            100 – 45            23 + 32

53 + 17            100 – 23            45 + 54

39 + 11            100 – 14            12 + 21

❸. По какому правилу записаны выражения в каждой паре?

2 + 1     4 + 3     6 + 2

1 + 2     3 + 4     2 + 6

❹. Разгадай правило, по которому составлены пары выражений. 

80 + 30     70 + 2     50 + 7

30 + 8       20 + 7     70 + 5

Запиши по тому же правилу пары выражений с другими числами.

❺. По какому правилу записаны выражения? Запиши в каждом ряду еще три выражения по тому же правилу?

а) 8 ∙ 2 + 1, 8 ∙ 3 + 2, 8 ∙ 4 + 3, …

б) 8 ∙ 9 – 9, 8 ∙ 8 – 8, 8 ∙ 7 – 7, …

❻.Догадайся, по какому признаку соединили выражения?

 

❼.Разгадай правило, по которому составлен первый столбик выражений. Составь по этому же правилу выражения для других столбиков.

Найди значения выражений.

24 + 5                23 + 6            47 + 2

24 + 50                   +                    + 

42 + 5                     +                    +

42 + 50                   +                  +

❽. По какому правилу записаны выражения? Запиши в каждом ряду еще три выражения по тому же правилу?

а) 8 ∙ 2 + 1, 8 ∙ 3 + 2, 8 ∙ 4 + 3, …

б) 8 ∙ 9 – 9, 8 ∙ 8 – 8, 8 ∙ 7 – 7, …

 

Первоначальное знакомство с понятиями не является окончательным. Понятие получает дальнейшее развитие. Это рассматривается в двух планах: уточнение содержания и объема понятия, выполнение новых действий с понятиями. 

Так как в начальной школе понятия в основном усваиваются на уровне представлений объектов и действий с ними, то необходимо учитывать некоторые методические требования при формировании понятий.

1.                 Как правило, нельзя начинать знакомство учащихся с понятием сразу с введения соответствующего термина. Такому знакомству должна предшествовать подготовительная работа, имеющая целью создание у детей достаточного запаса представлений об объектах, входящих в объем изучаемого понятия, потому что термин в той или иной мере обобщает. Исключение из этого требования составляют такие случаи, когда учащиеся практически уже подготовлены к введению новой терминологии, например, термины «трехзначные числа», «удобные слагаемые». Здесь изучение предшествующего материала одновременно готовит детей к новой терминологии. 

2.                 Так как понятия усваиваются  в действиях, которые выполняют с ними ученики, то необходимо предварительно выявить, какие действия должны усвоить дети при изучении данного понятия, и в соответствии с этим подбирать упражнения. При подборе упражнений важно учитывать закономерность: если в упражнениях какой-либо несущественный признак неоднократно сочетается с существенным, то нередко учащиеся несущественный признак относят также к существенным. Происходит неверное обобщение.  Например, при изучении числовых выражений их приходится сравнивать и поэтому ставить соответствующий знак между ними (равно, больше, меньше). Этот знак не является существенным для понятия «числовое выражение». Но он многократно повторяется, и ученики часто называют неравенства и равенства числовыми выражениями, что неверно. 

3.                 Для того чтобы дети правильно усваивали отличительные признаки изучаемых объектов, необходимо варьирование как существенных, так и несущественных признаков этих объектов. В практике обучения предложение о варьировании существенных признаков предметов выражается в короткой рекомендации: при изучении вновь вводимых понятий объекты из объема этих понятий следует показывать учащимся вместе с их противоположностью. Например: числовые равенства и числовые неравенства; числовые равенства и уравнения.

4.                 Для более глубокого усвоения понятий важно использовать не одно, а несколько действий: сравнение, выведение следствий, классификацию и др. Ценность и число действий, в которых функционирует данное понятие, и служит показателем качества его усвоения. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература

1.                 Аматова Г.М. Математика: в 2 кн. Кн.1 : уч.пособ.для студ.высш.пед.учеб.заведений /Г.М. Аматова, М.А. Аматов. – М.: Изд.центр «Академия», 2008.

2.                 Артемов А.К. Изучение математических понятий в начальных классах. -  Пенза, 1987.

3.                 Воровщиков С.Г. и др. Как эффективно развивать логическое мышление младших школьников: Управленческий и методический аспекты. – М.: 5 за знания, 2008.

4.                 Гин С.И. Мир логики. Программа и методические рекомендации по внеурочной деятельности в начальной школе: пособие для учителя 4 класса. – М.: ВИТА-ПРЕСС, 2013.

5.                 Демидова Т.Е., Козлова С.А., Тонких А.П. Моя математика:

Учебник для 1-го класса в 3-х частях. – М.: Изд.Дом РАО Баласс, 2011.

6.                 Демидова Т.Е., Козлова С.А., Тонких А.П. Моя математика:

Учебник для 2-го класса в 3-х частях. – М.: Изд.Дом РАО Баласс, 2011.

7.                 Демидова Т.Е., Козлова С.А., Тонких А.П. Моя математика:

Учебник для 3-го класса в 3-х частях. – М.: Изд.Дом РАО Баласс, 2012.

8.                 Демидова Т.Е., Козлова С.А., Тонких А.П. Моя математика:

Учебник для 4-го класса в 3-х частях. – М.: Изд.Дом РАО Баласс, 2013.

9.                 Истомина Н.Б. : учебник для 1 класса общеобразовательных учреждений. В двух частях. /Н.Б. Истомина. – 11-е изд.перераб. и доп. – Смоленск: Ассоциация XXI век, 2011.

10.             Истомина Н.Б.:  учебник для 2 класса общеобразовательных учреждений. В двух частях. /Н.Б. Истомина. – 11-е изд.перераб. и доп. – Смоленск: Ассоциация XXI век, 2011.

11.             Истомина Н.Б.:  учебник для 3 класса общеобразовательных учреждений. В двух частях. /Н.Б. Истомина. – 11-е изд.перераб. и доп. – Смоленск: Ассоциация XXI век, 2012.

12.             Истомина Н.Б.: учебник для 4 класса общеобразовательных учреждений. В двух частях. /Н.Б. Истомина. – 11-е изд.перераб. и доп. – Смоленск: Ассоциация XXI век, 2013.

13.             Истомина Н.Б. Методика обучения математике в начальной школе:

Развивающее обучение. – Смоленск: Изд-во «Ассоциация XXI век», 2005.

14.             Математика. 1 класс. Учеб.для общеобраз.учрежд. В 2 ч. [М.И.

Моро, М.А. Бантова, Г.В. Бельтюкова и др.]. – М.: Просвещение, 2011.

15.             Математика. 2 класс. Учеб.для общеобраз.учрежд. В 2 ч. [М.И.

Моро, М.А. Бантова, Г.В. Бельтюкова и др.]. – М.: Просвещение, 2011.

16.             Математика. 3 класс. Учеб.для общеобраз.учрежд. В 2 ч. [М.И.

Моро, М.А. Бантова, Г.В. Бельтюкова и др.]. – М.: Просвещение, 2012.

17.             Математика. 4 класс. Учеб.для общеобраз.учрежд. В 2 ч. [М.И.

Моро, М.А. Бантова, Г.В. Бельтюкова и др.]. – М.: Просвещение, 2013.

18.             Математика.        Сборник     задач:         уч.пособие для

студ.учрежд.высш.проф.образования / [Л.П. Стойлова. Е.А. Конобеева, Т.А. Конобеева, И.В. Шадрина]. – М.: Изд.центр «Акдемия», 2012. – (Сер. Бакалавриат).

19.             Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч.ред. Н.Л.Стефановой,

Н.С.Подходовой. – М.: Дрофа, 2008. – 415с.

20.             Полунина И.А., Стойлова Л.П. Задачи на распознавание в начальном курсе математики и проблемы обучения их решению //Начальная школа, 2010, №1.

21.             Стойлова Л.П. Основы начального курса математики – М.:

Просвещение, 2000.

22.             Талызина Н.Ф. Формирование познавательной деятельности младших школьников. М., 1998.

23.             Туркина В.М. Задания для формирования математических понятий  // Начальная школа. 1988. № 12.

24.             Фридман Л.М. Теоретические основы методики обучения математики: Учебное пособие. – М.: Книжный дом «ЛИБРОКОМ»,

2009.