Решение геометрических задач при подготовке к ОГЭ

Подготовка к ОГЭ по математике

Подборка материала

Цель: обеспечение подготовки учащихся 9-х классов к прохождению итоговой аттестации на основе некоторых тем по геометрии.

Задачи: формирование навыков, обеспечивающих успешное прохождение итоговой аттестации; умение пользоваться формулами для нахождения величин по условию задач; отработка вычислительных навыков при решении задач разного характера.

Разделы:

Прямоугольный треугольник

Трапеция

Центральные и впи­сан­ные углы

Касательная, хорда, секущая, радиус

Окружность, описанная вокруг многоугольника

Вариант № 1

Прямоугольный треугольник

1. 

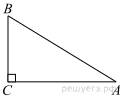В тре­уголь­ни­ке ABC угол C прямой, BC = 8 , sin A = 0,4.   Найдите AB.

2.  Два ост­рых угла пря­мо­уголь­но­го тре­уголь­ни­ка от­но­сят­ся как 4:5. Най­ди­те боль­ший ост­рый угол. Ответ дайте в градусах.

3. 

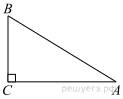В тре­уголь­ни­ке    угол    равен 90°,  . Най­ди­те  .

4. 

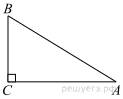В тре­уголь­ни­ке    угол    равен 90°,  .  Найдите  .

5. 

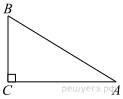В тре­уголь­ни­ке    угол    прямой,  . Най­ди­те  .

6. 

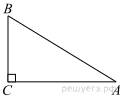В тре­уголь­ни­ке    угол    прямой,  . Най­ди­те  .

7.  В тре­уголь­ни­ке ABC угол C равен 90°, AC = 20, tgA = 0,5. Най­ди­те BC.

8.  В тре­уголь­ни­ке ABC угол C равен 90°, BC = 20,  = 0,5. Най­ди­те AC.

9.  В тре­уголь­ни­ке ABC угол C равен 90°, BC = 12 , tgA = 1,5. Най­ди­те AC.

10.  В тре­уголь­ни­ке ABC угол C равен 90°, AC = 12 , tgA = 1,5. Най­ди­те BC.

11.  Ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны 35 и 120. Най­ди­те вы­со­ту, про­ве­ден­ную к ги­по­те­ну­зе.

12. 

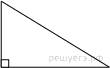Ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны  и 1. Най­ди­те синус наи­мень­ше­го угла этого тре­уголь­ни­ка.

13. 

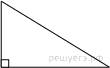Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна  Один из ост­рых углов равен 30°. Най­ди­те длину ги­по­те­ну­зы.

14. 

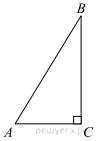В тре­уголь­ни­ке  угол  равен 90°,   Най­ди­те 

15. 

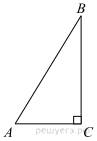В тре­уголь­ни­ке  угол  равен 90°,   Най­ди­те 

16. 

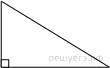Площадь пря­мо­уголь­но­го тре­уголь­ни­ка равна  Один из ост­рых углов равен 30°. Най­ди­те длину катета, ле­жа­ще­го на­про­тив этого угла.

17. 

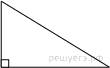Площадь пря­мо­уголь­но­го тре­уголь­ни­ка равна  Один из ост­рых углов равен 30°. Най­ди­те длину катета, при­ле­жа­ще­го к этому углу.

18.  Точка H яв­ля­ет­ся ос­но­ва­ни­ем высоты, проведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­ка ABC к ги­по­те­ну­зе AC. Най­ди­те AB, если AH = 6, AC = 24.

19. 

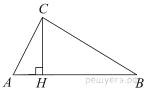В пря­мо­уголь­ном тре­уголь­ни­ке  катет , а вы­со­та , опу­щен­ная на гипотенузу, равна  Най­ди­те 

20. 

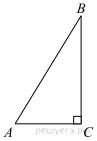В тре­уголь­ни­ке ABC угол C равен 90°, AC = 4, tg A = 0,75. Най­ди­те BC.

21. 

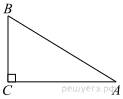В тре­уголь­ни­ке   = 35,  угол  равен 90°. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого треугольника.

22. 

Найдите пло­щадь пря­мо­уголь­но­го треугольника, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 12 и 13.

23. 

Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

24. 

В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.

25. 

В прямоугольном треугольнике катет и гипотенуза равны 40 и 50 соответственно. Найдите другой катет этого треугольника.

26. 

В треугольнике  известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

27. 

Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

28. 

В треугольнике  известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

29. 

В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

30. 

В треугольнике  известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

31. 

В треугольнике  угол  равен 90°, , . Найдите .

32. 

В треугольнике  известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

33. 

В треугольнике  известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

34. 

В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

35. 

В треугольнике  угол  равен 90°, , . Найдите .

36. 

В треугольнике  угол  равен 90°, , . Найдите .

37.  В треугольнике  угол  равен 90°, , . Найдите .

38. 

В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

39. 

В треугольнике  угол  равен 90°, , . Найдите .

40. 

В треугольнике  угол  равен 90°, , . Найдите .

41. 

В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

42. 

Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.

43. 

В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

44. 

В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

45. 

Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.

46. 

В треугольнике  известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

47. 

В треугольнике  угол  равен 90°, , . Найдите .

48. 

В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

49. 

Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

50. 

В прямоугольном треугольнике катет и гипотенуза равны 5 и 13 соответственно. Найдите другой катет этого треугольника.

51. 

В треугольнике  известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

52. 

Два катета прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.

53. 

Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.

54.  В треугольнике  угол  равен 90°, , . Найдите .

55.  Точка H яв­ля­ет­ся ос­но­ва­ни­ем высоты, проведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­ка ABC к ги­по­те­ну­зе AC.  Най­ди­те AB, если AH = 8, AC = 32.

Трапеция

1. 

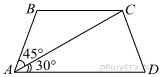Найдите боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной AB углы, рав­ные 30° и 45° соответственно.

2. 

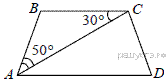Найдите угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 50° соответственно.

3.  Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 140°. Най­ди­те боль­ший угол трапеции. Ответ дайте в градусах.

4.  Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 220°. Най­ди­те мень­ший угол трапеции. Ответ дайте в градусах.

5.  Найдите мень­ший угол рав­но­бед­рен­ной трапеции, если два ее угла от­но­сят­ся как 1:2. Ответ дайте в градусах.

6.  Основания тра­пе­ции равны 4 см и 10 см. Диа­го­наль трапеции делит сред­нюю линию на два отрезка. Най­ди­те длину боль­ше­го из них.

7. 

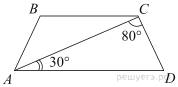Найдите угол  ABC  рав­но­бед­рен­ной тра­пе­ции  ABCD, если диа­го­наль  AC  об­ра­зу­ет с ос­но­ва­ни­ем  AD и бо­ко­вой сто­ро­ной  CD  углы, рав­ные 30° и 80° соответственно.

8. 

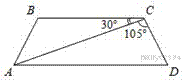Найдите мень­ший угол рав­но­бед­рен­ной тра­пе­ции  ABCD, если диа­го­наль  AC  об­ра­зу­ет с ос­но­ва­ни­ем  BC  и бо­ко­вой сто­ро­ной  CD  углы, рав­ные 30° и 105° соответственно.

9. 

Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен   Най­ди­те её боль­шее основание, если мень­шее ос­но­ва­ние равно вы­со­те и равно 15.

10. 

Най­ди­те угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 40° со­от­вет­ствен­но.

11. 

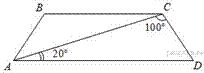
Най­ди­те угол АВС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной CD углы, рав­ные 20° и 100° со­от­вет­ствен­но.

12. 

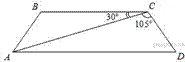Най­ди­те мень­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной CD углы, рав­ные 30° и 105° со­от­вет­ствен­но.

13. 

Най­ди­те боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной АВ углы, рав­ные 25° и 40° со­от­вет­ствен­но.

14. 

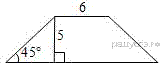В рав­но­бед­рен­ной тра­пе­ции из­вест­ны вы­со­та, мень­шее ос­но­ва­ние и угол при ос­но­ва­нии. Най­ди­те боль­шее ос­но­ва­ние.

15. 

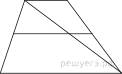Ос­но­ва­ния тра­пе­ции равны 4 и 10. Най­ди­те боль­ший из от­рез­ков, на ко­то­рые делит сред­нюю линию этой тра­пе­ции одна из её диа­го­на­лей.

16. 

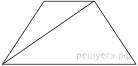Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 50 и 104, бо­ко­вая сто­ро­на 45. Най­ди­те длину диа­го­на­ли тра­пе­ции.

17.  Около тра­пе­ции, один из углов ко­то­рой равен 49°, опи­са­на окруж­ность. Най­ди­те осталь­ные углы тра­пе­ции. Запишите ве­ли­чи­ны углов в ответ без пробелов в по­ряд­ке неубывания.

18.  В тра­пе­цию, сумма длин бо­ко­вых сто­рон ко­то­рой равна 24, впи­са­на окруж­ность. Най­ди­те длину сред­ней линии тра­пе­ции.

19.  Биссектрисы углов A и B при бо­ко­вой сто­ро­не AB тра­пе­ции ABCD пе­ре­се­ка­ют­ся в точке F. Най­ди­те AB, если AF = 24, BF = 32.

20. 

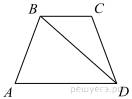В тра­пе­ции ABCD AB = CD, ∠BDA = 49° и ∠BDC = 13°. Най­ди­те угол ABD. Ответ дайте в градусах.

21. 

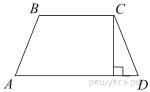Высота рав­но­бед­рен­ной трапеции, проведённая из вер­ши­ны C, делит ос­но­ва­ние AD на от­рез­ки дли­ной 1 и 5. Най­ди­те длину ос­но­ва­ния BC.

Центральные и впи­сан­ные углы

1. 

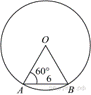Цен­траль­ный угол AOB опи­ра­ет­ся на хорду AB дли­ной 6. При этом угол OAB равен 60°. Най­ди­те радиус окружности.

2. 

В окруж­но­сти с цен­тром в точке О про­ве­де­ны диаметры AD и BC, угол OCD равен 30°. Най­ди­те величину угла OAB.

3. 

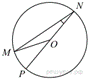Найдите гра­дус­ную меру центрального ∠MON, если известно, NP — диаметр, а гра­дус­ная мера ∠MNP равна 18°.

4. 

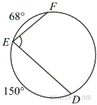Найдите ∠DEF, если гра­дус­ные меры дуг DE и EF равны 150° и 68° соответственно.

5. 

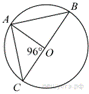Найдите гра­дус­ную меру ∠ACB, если известно, что BC яв­ля­ет­ся диа­мет­ром окружности, а гра­дус­ная мера центрального ∠AOC равна 96°.

6. 

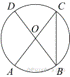В окруж­но­сти с цен­тром O AC и BD — диаметры. Угол ACB равен 26°. Най­ди­те угол AOD. Ответ дайте в градусах.

7. 

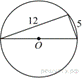Прямоугольный тре­уголь­ник с ка­те­та­ми 5 см и 12 см впи­сан в окружность. Чему равен ра­ди­ус этой окружности?

8. 

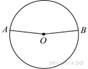Точки A и B делят окруж­ность на две дуги, длины ко­то­рых относятся как 9:11. Най­ди­те величину цен­траль­но­го угла, опи­ра­ю­ще­го­ся на мень­шую из дуг. Ответ дайте в градусах.

9. 

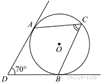В угол ве­ли­чи­ной 70° впи­са­на окружность, ко­то­рая ка­са­ет­ся его сто­рон в точ­ках A и B. На одной из дуг этой окруж­но­сти вы­бра­ли точку C так, как по­ка­за­но на рисунке. Най­ди­те ве­ли­чи­ну угла ACB.

10. 

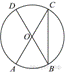Величина цен­траль­но­го угла AOD равна 110°. Най­ди­те величину впи­сан­но­го угла ACB. Ответ дайте в градусах.

11. 

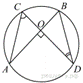Точки A, B, C и D лежат на одной окруж­но­сти так, что хорды AB и СD вза­им­но перпендикулярны, а ∠BDC = 25°. Най­ди­те величину угла ACD.

12. 

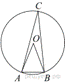Треугольник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 48°.

13. 

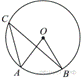Точка О — центр окруж­но­сти, ∠AOB = 84° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла ACB (в гра­ду­сах).

14. 

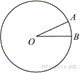На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что  Длина мень­шей дуги AB равна 63. Най­ди­те длину боль­шей дуги.

15. 

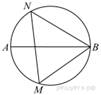На окруж­но­сти по раз­ные стороны от диа­мет­ра AB взяты точки M и N. Известно, что ∠NBA = 38°. Най­ди­те угол NMB. Ответ дайте в градусах.

16. 

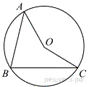Точка O – центр окружности, на ко­то­рой лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°. Най­ди­те угол BCO. Ответ дайте в градусах.

17. 

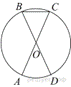AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 79°. Най­ди­те угол AOD. Ответ дайте в градусах.

18. 

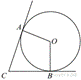В угол C ве­ли­чи­ной 83° впи­са­на окружность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B. Най­ди­те угол AOB. Ответ дайте в градусах.

19. 

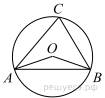Треугольник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 115°.

20. 

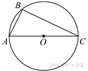Сторона AC тре­уголь­ни­ка ABC со­дер­жит центр опи­сан­ной около него окружности. Най­ди­те , если . Ответ дайте в градусах.

21. 

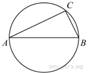Центр окружности, описанной около треугольника ABC, лежит на сторонеAB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.

22.  На окружности с центром в точке  отмечены точки  и  так, что . Длина меньшей дуги  равна 50. Найдите длину большей дуги .

23. 

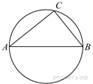Центр окружности, описанной около треугольника , лежит на стороне . Найдите угол , если угол  равен 44°. Ответ дайте в градусах.

24. 

В угол  величиной 157° вписана окружность, которая касается сторон угла в точках  и , точка  — центр окружности. Найдите угол . Ответ дайте в градусах.

25. 

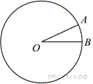На окружности с центром в точке  отмечены точки  и  так, что . Длина меньшей дуги  равна 5. Найдите длину большей дуги .

26. 

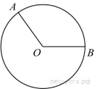На окружности с центром в точке  отмечены точки  и  так, что . Длина меньшей дуги  равна 61. Найдите длину большей дуги .

27. 

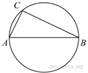Центр окружности, описанной около треугольника , лежит на стороне . Радиус окружности равен 6,5. Найдите , если 

28. 

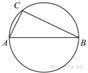Центр окружности, описанной около треугольника , лежит на стороне . Радиус окружности равен 8,5. Найдите , если .

29. 

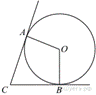В угол C ве­ли­чи­ной 72° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B, точка O - центр окружности. Най­ди­те угол AOB. Ответ дайте в гра­ду­сах.

30. 

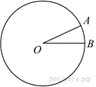На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что  Длина мень­шей дуги AB равна 98. Най­ди­те длину боль­шей дуги.

31. 

На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что  Длина мень­шей дуги AB равна 58. Най­ди­те длину боль­шей дуги.

32. 

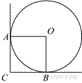В угол C ве­ли­чи­ной 90° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B, точка O - центр окружности. Най­ди­те угол AOB. Ответ дайте в гра­ду­сах.

33. 

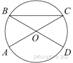AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 36°. Най­ди­те угол AOD. Ответ дайте в градусах.

34. 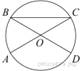 AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 23°. Най­ди­те угол AOD. Ответ дайте в градусах.

35. 

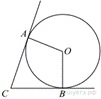В угол C ве­ли­чи­ной 62° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B, точка O — центр окружности. Най­ди­те угол AOB. Ответ дайте в гра­ду­сах.

36. 

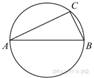Центр окружности, описанной около треугольника ABC, лежит на сторонеAB. Найдите угол ABC, если угол BAC равен 33°. Ответ дайте в градусах.

37. 

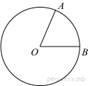На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что  Длина мень­шей дуги AB равна 57. Най­ди­те длину боль­шей дуги.

38. 

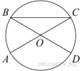AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 54°. Най­ди­те угол AOD. Ответ дайте в градусах.

39. 

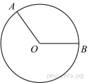На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что  Длина мень­шей дуги AB равна 67. Най­ди­те длину боль­шей дуги.

40. 

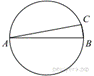Центр окружности, описанной около треугольника ABC, лежит на сторонеAB. Найдите угол ABC, если угол BAC равен 9°. Ответ дайте в градусах.

41. 

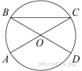AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 19°. Най­ди­те угол AOD. Ответ дайте в градусах.

42. 

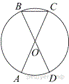AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 78°. Най­ди­те угол AOD. Ответ дайте в градусах.

43. 

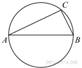Центр окружности, описанной около треугольника ABC, лежит на сторонеAB. Найдите угол ABC, если угол BAC равен 24°. Ответ дайте в градусах.

44. 

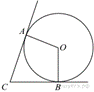В угол C ве­ли­чи­ной 71° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B, точка O - центр окружности. Най­ди­те угол AOB. Ответ дайте в гра­ду­сах.

Касательная, хорда, секущая, радиус

1. 

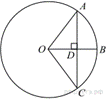Радиус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окружности равен 5 см.

2. 

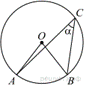Найдите ве­ли­чи­ну (в градусах) впи­сан­но­го угла α, опи­ра­ю­ще­го­ся на хорду  AB, рав­ную ра­ди­у­су окружности.

3. 

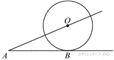К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окружности, если AB = 12 см, AO = 13 см.

4. 

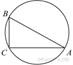В тре­уголь­ни­ке ABC угол C равен 90°, AC = 30 , BC =  Най­ди­те ра­ди­ус окружности, опи­сан­ной около этого треугольника.

5. 

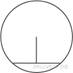Длина хорды окруж­но­сти равна 72, а рас­сто­я­ние от цен­тра окруж­но­сти до этой хорды равно 27. Най­ди­те диа­метр окруж­но­сти.

6.  Вер­ши­ны тре­уголь­ни­ка делят опи­сан­ную около него окруж­ность на три дуги, длины ко­то­рых от­но­сят­ся как 3:4:11. Най­ди­те ра­ди­ус окруж­но­сти, если мень­шая из сто­рон равна 14.

7. 

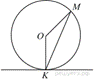Прямая ка­са­ет­ся окруж­но­сти в точке K. Точка O — центр окружности. Хорда KM об­ра­зу­ет с ка­са­тель­ной угол, рав­ный 83°. Най­ди­те ве­ли­чи­ну угла OMK. Ответ дайте в градусах.

8.  Отрезки AB и CD яв­ля­ют­ся хор­да­ми окружности. Най­ди­те длину хорды CD, если AB = 20, а рас­сто­я­ния от цен­тра окруж­но­сти до хорд AB и CD равны со­от­вет­ствен­но 24 и 10.

9.  Отрезки AB и CD яв­ля­ют­ся хор­да­ми окружности. Най­ди­те рас­сто­я­ние от цен­тра окруж­но­сти до хорды CD, если AB = 18, CD = 24, а рас­сто­я­ние от цен­тра окруж­но­сти до хорды AB равно 12.

10.  На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что ∠AOB = 66°. Длина мень­шей дуги AB равна 99. Най­ди­те длину боль­шей дуги.

11. 

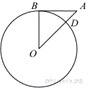Отрезок AB = 40 ка­са­ет­ся окруж­но­сти ра­ди­у­са 75 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

12. 

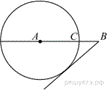На от­рез­ке AB вы­бра­на точка C так, что AC = 75 и BC = 10. По­стро­е­на окружность с цен­тром A, про­хо­дя­щая через C. Най­ди­те длину от­рез­ка касательной, проведённой из точки B к этой окружности.

13. 

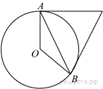Касательные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 72°. Най­ди­те угол ABO. Ответ дайте в градусах.

14. 

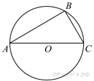Сторона AC тре­уголь­ни­ка ABC про­хо­дит через центр опи­сан­ной около него окружности. Най­ди­те ∠C , если ∠A = 44°. Ответ дайте в градусах.

15. 

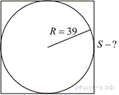Окружность впи­са­на в квадрат. Най­ди­те пло­щадь квадрата.

16. 

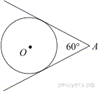Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точкеО. Най­ди­те ра­ди­ус окружности, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

17.  Окружность с цен­тром на сто­ро­не AC тре­уголь­ни­ка ABC про­хо­дит через вер­ши­ну C и ка­са­ет­ся пря­мой AB в точке B. Най­ди­те AC, если диа­метр окруж­но­сти равен 7,5, а AB = 2.

18. 

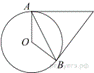Касательные в точках  и  к окружности с центром  пересекаются под углом 76°. Найдите угол . Ответ дайте в градусах.

19. 

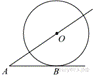К окружности с центром в точке  проведены касательная  и секущая . Найдите радиус окружности, если , .

20. 

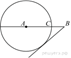На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

21. 

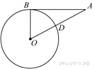Отрезок  касается окружности радиуса 24 с центром  в точке . Окружность пересекает отрезок  в точке . Найдите .

22. 

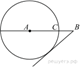На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

23. 

К окружности с центром в точке  проведены касательная  и секущая . Найдите радиус окружности, если , .

24. 

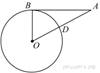Отрезок  касается окружности радиуса 54 с центром  в точке . Окружность пересекает отрезок  в точке . Найдите .

25. 

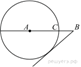На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

26. 

К окружности с центром в точке  проведены касательная  и секущая . Найдите радиус окружности, если , 

27. 

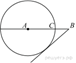На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

28. 

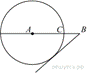На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

29. 

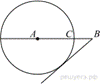На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

30. 

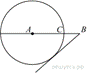На отрезке  выбрана точка  так, что  и . Построена окружность с центром , проходящая через . Найдите длину отрезка касательной, проведённой из точки  к этой окружности.

31. 

Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.

Окружность, описанная вокруг многоугольника

1. 

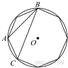В окруж­ность вписан рав­но­сто­рон­ний восьмиугольник. Най­ди­те величину угла ABC.

2. 

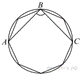В окруж­ность впи­сан рав­но­сто­рон­ний восьмиугольник. Най­ди­те ве­ли­чи­ну угла ABC.

3.  Боковая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 4. Угол при вершине, про­ти­во­ле­жа­щий основанию, равен 120°. Най­ди­те диа­метр окружности, опи­сан­ной около этого треугольника.

4.  Боковая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 5. Угол при вершине, про­ти­во­ле­жа­щий основанию, равен 120°. Най­ди­те диа­метр окружности, опи­сан­ной около этого треугольника.

5. 

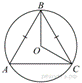Окружность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го треугольника ABC, в ко­то­ром AB = BC и ∠ABC = 177°. Най­ди­те величину угла BOC. Ответ дайте в градусах.

6. 

 Четырехугольник ABCD впи­сан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Най­ди­те угол ABD. Ответ дайте в градусах.

7. 

Найдите пло­щадь квадрата, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 7.

Вариант № 1

1.  Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без пробелов и других дополнительных символов.

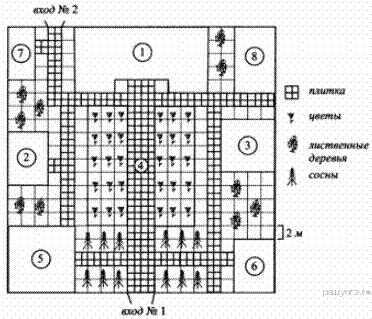
На плане (см. рисунок) представлен дизайн‐проект сквера в станице Лужки. Сторона большой клетки равна 2 метра. Участок, отведённый под сквер, имеет квадратную форму. По периметру участка планируется установить забор. С двух сторон сквера будут два входа.

Если зайти в сквер, то справа от входа № 1 будет располагаться карусель, а слева — детский игровой комплекс, отмеченный на плане цифрой 5.

Дом творчества будет находиться слева, если зайти через вход № 2, а зооуголок — справа.

Центр сквера, отмеченный цифрой 4, планируется украсить фонтаном диаметром 2 метра и двумя цветочными клумбами. Рядом с детским игровым комплексом построят кафе, рядом с каруселью — кинотеатр площадью 64 м2.

За кинотеатром будет оборудована тренажёрная площадка, отмеченная цифрой 8.

На территории сквера шириной 2 м будут выложены тротуарной плиткой. Размером 1 м × 1 м. Аллея шириной 4 м располагается от входа № 1 до Дома творчества и выложена той же плиткой, что и дорожки.

2.  Тротуарная плитка продаётся в упаковках по 3 штуки. Сколько упаковок понадобится купить, чтобы выложить аллею от входа № 1 до Дома творчества?

3.  Найдите площадь (в м2) земли, которую занимает Дом творчества.

4.  Найдите наибольший возможный радиус карусели (в метрах).

5.  При обсуждении, каким должен быть забор, рассматривалось два варианта: кованый или комбинированный. Цены на доставку оборудования и на установочные работы, а также стоимость изготовления одного погонного метра забора представлены в таблице. На сколько рублей общая стоимость кованного забора меньше общей стоимости комбинированного забора? 

 Примечание. При входах забор не устанавливается.

6.  Най­ди­те зна­че­ние вы­ра­же­ния

7.  На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа a и b.

 Какое из сле­ду­ю­щих чисел наибольшее?

В ответе укажите номер правильного варианта.

1) a + b            2) –a             3) 2b            4) a – b

8.  Вычислите: В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1)             2)               3)            4) 

9.  Решите си­сте­му уравнений 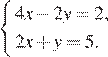  В ответе запишите сумму решений системы.

10.  В денежно-вещевой ло­те­рее на 100 000 би­ле­тов разыг­ры­ва­ет­ся 1300 ве­ще­вых и 850 де­неж­ных выигрышей. Ка­ко­ва ве­ро­ят­ность по­лу­чить ве­ще­вой выигрыш?

11.  На одном из ри­сун­ков изоб­ра­же­на парабола. Ука­жи­те номер этого рисунка.

12.  Какое наи­боль­шее число по­сле­до­ва­тель­ных на­ту­раль­ных чисел, на­чи­ная с 1, можно сло­жить, чтобы по­лу­чив­ша­я­ся сумма была мень­ше 528?

13.  Найдите значение выражения: 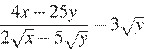, если 

14.  Из фор­му­лы цен­тро­стре­ми­тель­но­го уско­ре­ния a = ω2R най­ди­те R (в метрах), если ω = 4 с−1 и a = 64 м/с2.

15.  На каком ри­сун­ке изоб­ра­же­но мно­же­ство ре­ше­ний не­ра­вен­ства 

В ответе укажите номер правильного варианта.

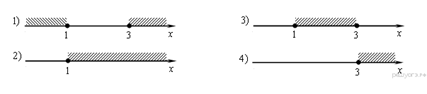
16.  Основания тра­пе­ции равны 4 см и 10 см. Диа­го­наль трапеции делит сред­нюю линию на два отрезка. Най­ди­те длину боль­ше­го из них.

17.  Боковая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 4. Угол при вершине, про­ти­во­ле­жа­щий основанию, равен 120°. Най­ди­те диа­метр окружности, опи­сан­ной около этого треугольника.

18.  Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а тан­генс одного из углов равен . Най­ди­те площадь параллелограмма.

19. 

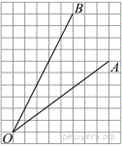Найдите тангенс угла . Размер клетки 1 × 1.

20.  Какое из следующих утверждений верно?

1. Все углы ромба равны.

2. Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности. В ответ запишите номер выбранного утверждения.

21.  Разложите на множители: .

22.  Све­жие фрук­ты со­дер­жат 80% воды, а вы­су­шен­ные — 28%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 288 кг све­жих фрук­тов?

23.  Постройте гра­фик функ­ции  и определите, при каких зна­че­ни­ях  пря­мая  имеет с гра­фи­ком ровно одну общую точку.

24.  Окружность, впи­сан­ная в тре­уголь­ник ABC , ка­са­ет­ся его сто­рон в точ­ках M, K и P. Най­ди­те углы тре­уголь­ни­ка ABC, если углы тре­уголь­ни­ка MKP равны 49°, 69° и 62°.

25.  В тре­уголь­ни­ке ABC с тупым углом ACB про­ве­де­ны вы­со­ты AA1 и BB1. Докажите, что тре­уголь­ни­ки A1CB1 и ACB подобны.

26.  В па­рал­ле­ло­грам­ме ABCD про­ве­де­на диа­го­наль AC. Точка O яв­ля­ет­ся цен­тром окружности, впи­сан­ной в тре­уголь­ник ABC. Рас­сто­я­ния от точки O до точки A и пря­мых AD и AC со­от­вет­ствен­но равны 5, 4 и 3. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма ABCD.