
Решение
различных задач,
связанных с преобразованием выражений,
содержащих квадратные корни
Цели: закрепить знания и умения учащихся по преобразованию выражений, содержащих квадратные корни.
Ход урока
I. Организационный момент.
II. Устная работа.
– Приведите подобные слагаемые:
а) ![]() ; д)
; д)
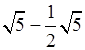 ;
;
б) 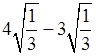 ; е)
; е)
![]() ;
;
в) ![]() ; ж)
; ж)
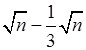 ;
;
г) ![]() ; з)
; з)
![]() .
.
III. Формирование умений и навыков.
На этом уроке учащиеся выполняют более сложные задания на преобразование выражений, содержащих квадратные корни. Все задания можно разбить на две группы. Во вторую группу войдут задания повышенного уровня сложности, поэтому их можно не выполнять в классе с низким уровнем подготовки.
1-я г р у п п а.
1. № 436 (а, в, д), № 437.
2. № 435 (а, в).
3. № 434.
Р е ш е н и е
а) Преобразуем данное выражение:
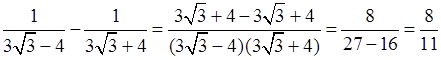 .
.
Таким образом, значение выражения является рациональным числом.
б) 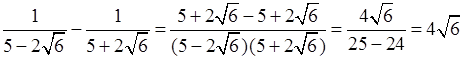 .
.
Таким образом, значение выражения является иррациональным числом.
4. № 438.
Р е ш е н и е
Известно, что взаимно-обратные числа в произведении дают единицу, а противоположные числа в сумме дают ноль.
![]() = 4 – 3 = 1, то есть данные
числа являются взаимно-обратными.
= 4 – 3 = 1, то есть данные
числа являются взаимно-обратными.
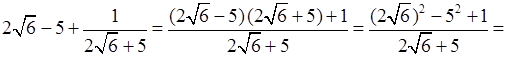
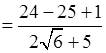 = 0, то есть данные числа
являются противоположными.
= 0, то есть данные числа
являются противоположными.
2-я г р у п п а.
1. № 508.
Р е ш е н и е
– Сначала сократим данную дробь:
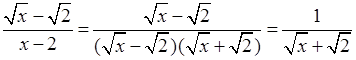 .
.
Так как выражение ![]() положительно
при любых х, то дробь
положительно
при любых х, то дробь 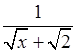 принимает наибольшее
значение, когда её знаменатель наименьший. Выражение
принимает наибольшее
значение, когда её знаменатель наименьший. Выражение ![]() принимает
наименьшее значение при х = 0.
принимает
наименьшее значение при х = 0.
О т в е т: при х = 0.
2. № 511.
Р е ш е н и е
![]()
![]() .
.
Выражение ![]() + 7
положительно при всех допустимых значениях b, поэтому
+ 7
положительно при всех допустимых значениях b, поэтому ![]() .
.
По условию 0 ≤ b ≤ 49, при
таких значениях b выражение ![]() – 7
меньше либо равно нулю, поэтому
– 7
меньше либо равно нулю, поэтому ![]() .
.
Таким образом, имеем:
![]() = 14, то есть исходное
выражение не зависит от b.
= 14, то есть исходное
выражение не зависит от b.
3. Докажите, что верно равенство:
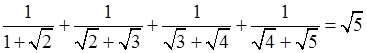 – 1.
– 1.
Р е ш е н и е
– Освободимся от иррациональности в знаменателе каждой дроби:
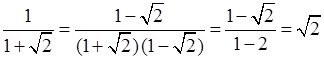 – 1;
– 1;
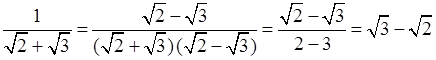 ;
;
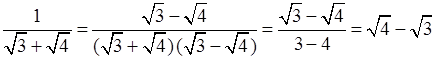 ;
;
 .
.
Преобразуем левую часть исходного равенства, подставляя в него полученные выражения:
![]() – 1
– 1
![]() – 1.
– 1.
Равенство доказано.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется арифметическим квадратным корнем из числа а?
– Сформулируйте все свойства арифметического квадратного корня.
– В чём состоит приём вынесения множителя из-под знака корня? внесения множителя под знак корня? Когда используются эти приёмы?
– Как освободиться от иррациональности в знаменателе дроби?
Домашнее задание: № 435 (б, г), № 436 (б, г, е), № 439.
Д о п о л н и т е л ь н о: № 506 (в, г).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.