
ЭКЗАМЕН ПО ИНФОРМАТИКЕ
Л. М. Дергачева
ЭКЗАМЕНАЦИОННЫХ ЗАДАЧ
ПО ИНФОРМАТИКЕ
Л. М. Дергачева
Р Е Ш Е Н И Е ТИ П ОВ Ы Х ЭКЗАМЕНАЦИОННЫХ ЗАДАЧ по иноорммике
Москва
БИНОМ. Лаборатория знаний
2013
удк 004.9 ББК 32.97
Д36
Сер ия о с н о ва н а в 2007 г.
Дергачева Л. М.
Д36 Решение типовых экзаменационных задач по информатике : учебное пособие / Л. М. Дергачева. — М. : БИНОМ. Лаборатория знаний, 2013. —360с. . ил. — (Экзамен по информатике).
ISBN 9785-9963-0484-4
Пособие входит в состав серии «Экзамен по информатике» и содержит решения типовых задач по информатике, предлагаемых на Едином государственном экзамене. Пособие может использоваться учителями информатики при подготовке, планировании и проведении уроков, а также учащимися для самостоятельной подготовки к вступительным испытаниям в высшие учебные заведения и средние специальные учреждения.
Для учащихся 10—11 классов, учителей информатики и ИКТ, методистов и студентов педагогических вузов.
удк 004.9 БЫС 32.97
![]()
Учебное изДание
Серия: «Экзамен по информатике»
Дергачева Лариса Михайловна
РЕШЕНИЕ типовых ЭКЗАМЕНАЦИОННЫХ ЗАДАЧ
ПО ИНФОРМАТИКЕ
Учебное пособие
Научный редактор Н. Н. Самылкина
Ведущий редактор Д. Ю. Усенков
Художник Н. А. Новак
Технический редактор Е. В. Денюкова
Корректор Е. Н. Клитина
Компьютерная верстка: В. А. Носенко
Подписано в печать 23.11.12. Формат 70х 100/16.
Усл. печ. л. 29,25. Тираж 2000 экз. Заказ 9355
Издательство «БИНОМ. Лаборатория знаний» 125167, Москва, проезд Аэропорта, д. З
Телефон: (499) 157-5272, e-mail: binom@Lbz.ru, http://www.Lbz.ru при участии 000 «ЭМПРЕЗА»
Отпечатано в ОАО «Первая Образцовая типография», филиал «УЛЬЯНОВСКИЙ ДОМ ПЕЧАТИ». 432980. г. Ульяновск. ул. Гончарова, 14
![]()
С) БИНОМ. Лаборатория знаний,
ISBN 978-5-9963-04844 2012
Оглавление
Р а з дел 1 . Информация и ее кодирование ![]() . . 5
. . 5
Виды
информационных процессов. Процесс передачи информации. Сигнал, кодирование и
декодирование информации. Дискретное (цифровое) представление текстовой,
графической, звуковой информации и видеоинформации. . . . . . . . . . . . . ![]() Единицы
измерения количества информации. Вычисление информационного объема сообщения .
Единицы
измерения количества информации. Вычисление информационного объема сообщения .![]() .
19 Скорость передачи информации и пропускная способность канала передачи .
.
19 Скорость передачи информации и пропускная способность канала передачи .![]() .
32
.
32
Раздел 2. Моделирование![]() . 42
. 42
Описание (модель) реального объекта и
процесса, СООТВ&гСТвие описания объекту и целям описания. Схемы, таблицы,
графики, формулы как описания. . . . . . ![]() . 42
. 42
Раздел З. Системы счисления ![]() . . .. ... 57
Позиционные системы счисления .
. . .. ... 57
Позиционные системы счисления . ![]() .
57 Арифметические операции в двоичной системе счисления . . . .
.
57 Арифметические операции в двоичной системе счисления . . . . ![]() . 77
. 77
Раздел 4.
Логика и алгоритмы. . . . . . . . ![]()
Высказывания, логические операции,
кванторы, истинность высказывания ![]() . 88 Цепочки (конечные
последовательности), псевдослучайные последовательности. . . . . . . . . . .
. 88 Цепочки (конечные
последовательности), псевдослучайные последовательности. . . . . . . . . . . ![]() 134
134
Р а з дел 5 . Элементы теории алгоритмов ![]() . 178
. 178
Формализация понятия алгоритма ![]() . .
. . . . . . . . . . . . . . . . . . 178
. .
. . . . . . . . . . . . . . . . . . 178
Р а з дел 6 . Языки программирования![]() . 208
. 208
Типы данных . . . . . . . . . . . . . . . .![]() . 208
. 208
Основные конструкции языка
программирования. . . . . .![]() . 215
. 215
Р а з дел 7 .
Технология кодирования, создания и обработки текстовой, графической, числовой,
мультимедийной информации. Технология создания, хранения, поиска и сортировки
информации в базах данных. Файловая система . . . . ![]() . . 258 Технология создания и
обработки текстовой информации
. . 258 Технология создания и
обработки текстовой информации![]() . 258
. 258
Технология создания и обработки графической
информации . ![]() . 266
. 266
Оглавление
![]()
|
Математическая обработка
статистических данных . |
|
|
|
и расчетно-графических задач Системы управления базами данных. |
|
|
|
Организация баз данных. . . . . . . . |
|
|
|
(формирование запросов) . |
|
|
|
Файловая система . |
|
|
Р а з дел 8. Телекоммуникационные
технологии . . . . . . ![]() •
• ![]() . . 349 Инструменты создания
информационных объектов для Интернета
. . 349 Инструменты создания
информационных объектов для Интернета![]() . 349
. 349
Литература ![]() 358
358
Информация и ее кодирование
Виды информационных процессов. Процесс передачи информации. Сигнал, кодирование и декодирование информации. Дискретное (цифровое) представление текстовой, графической, звуковой информации и видеоинформации
1, Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется посимвольное кодирование: А — 00, Б —11, В — 010, Г — 011. Через канал связи передается сообщение: ВАГБГВ. Закодируйте это сообщение данным кодом. Полученную двоичную последовательность переведите в шестнадцатеричный вид.
1) AD34
2) 43DA
3) 101334
4) CADBCD
|
Дано: А = 002 Б- 112 в=0102 г=0112 |
Решение
Можно сразу заметить, что результатом будет являться четырехзначное шестнадцатеричное число, поскольку количество двоичных цифр равно пятнадцати, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому варианты ответов З и 4 отпадают сразу.
Ответ: 43DA16. |
|
Найти: ВАГБГВ16 _ ? |
Номер ответа: 2. |
![]()
2. Для кодирования букв А, Б, В, Г используются двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится:
|
Дано: А = 000 в=01 с = 100 D= 10 Е=О11 |
Решение Закодируем предложенные наборы букв и сравним полученный результат с двоичной строкой 0110100011000. ЕВСЕА = 01101100011000; BDDEA = 011010011000; BDCEA = 0110100011000; ЕВАЕА = 01101000011000. Таким образом, правильный номер ответа з. Ответ: BDCEA. |
|
Найти: 0110100011000 — ? |
Номер ответа: З. |
2) 411 3) BACD 4) 1023
|
Дано:
Б=012 |
Решение БАВГ2 = 010010112 = 4В16. Кроме того, можно сразу увидеть, что результатом будет являться двузначное шестнадцатеричное число, поскольку количество двоичных цифр равно восьми, а каждые четыре двоичные цифры соответствуют одной восьмеричной. Ответ: 4В16. |
|
Найти: БАВГ16 — |
Номер ответа: 1. |
З. Для пяти букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, а для некоторых — из трех). Эти коды представлены в таблице:
|
|
в |
с |
D |
|
|
000 |
01 |
100 |
10 |
011 |
Определить, какой набор букв закодирован двоичной строкой
0110100011000.
1) ЕВСЕА 2) ВТ)ЕА 3) BDCEA 4) ЕВАЕА
4. Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, использован неравномерный по длине код: А = О, Б = 10, В = 110. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
3) 111
|
Дано:
Б- 10 в= 110 |
Решение При решении данной задачи следует обратить внимание на то, что сообщение, записанное с помощью неравномерного по длине кода, однозначно декодируется только в том случае, если никакой код не является началом другого, более длинного кода. Рассмотрим самый короткий код для буквы Г: 1. Однако этот код совпадает с началом кодов букв Б и В, поэтому однозначное разбиение кодированного сообщения на буквы в данном случае невозможно. Код Г = 11 также не подходит, поскольку он совпадает с началом кода буквы В. Следующий код Г = 111 не является началом никакого уже известного кода; кроме того, ни один уже имеющийся код не является началом кода 111. Поэтому данный код является решением задачи. Ответ: 111. |
|
Найти:
|
Номер ответа: З. |
5. Черно-белое растровое изображение кодируется построчно, начиная с левого верхнего угла и заканчивая в правом нижнем углу. При кодировании 1 обозначает черный цвет, а О — белый.

Для компактности результат записали в шестнадцатеричной системе счисления. Выберите правильную запись такого кода.
1) BD9AA5 3) BDA9D5
2) BDA9B5 4) DB9DAB
Решение
Представим растровое изображение в виде однострочной цепочки пикселей:
![]()
Далее заменим черные ячейки единицами, а белые — нулями:
![]()
![]()
Переводя тетрады в шестнадцатеричную систему, получим следующую запись в шестнадцатеричной системе счисления: BDA9D5. Номер ответа: З.
6. Для кодирования букв А, Б, В, Г используются последовательные двухразрядные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБАВ и записать результат в шестнадцатеричной системе счисления, то получится:
1) 13216 2) D216 3) 310216 4) 2D16
|
Дано:
|
Решение ГБАВ = 110100102. Можно сразу заметить, что результатом будет являться двузначное шестнадцатеричное число, поскольку количество двоичных цифр равно восьми, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому варианты ответа 1, З и 4 сразу отпадают. ГБАВ = 110100102 = D216. Ответ: D216. |
|
Найти: ГБАВ16 — |
Номер ответа: 2. |
7. А, Б, В, Г последовательные двухразрядные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБВА и записать результат шестнадцатеричным кодом, то получится:
|
Дано:
Б=О12 в: 102 г- 11 2 |
Решение ГБАВ 2 = 110110002. Можно сразу заметить, что результатом будет являться двузначное шестнадцатеричное число, поскольку количество двоичных цифр равно восьми, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому единственный возможный вариант правильного ответа — З. Ответ: D816. |
|
Найти: ГБВА16 — ? |
Номер ответа: З. |
8. Для пяти букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, а для некоторых — из трех). Эти коды представлены в таблице:
|
а |
Ь |
с |
|
|
|
000 |
110 |
01 |
001 |
10 |
Определите, какой набор букв закодирован двоичной строкой
1100000100110:
1) baade 2) badde З) bacde 4) bacdb
|
Дано: а = 0002 ь- 110 2 с- 012
|
Решение Закодируем предложенные наборы букв и сравним полученный результат с двоичной строкой 1100000100110. baade = 11000000000110; badde = 11000000100110; bacde = 1100000100110; bacdb = 11000001001110. Таким образом, правильный номер ответа—3. Ответ: bacde. |
|
Найти: 1100000100110 —9 |
Номер ответа: З. |
9. Для кодирования А, Б, В, Г последовательные четырехразрядные двоичные числа от 1000 до 1011 соответственно. Если таким способом закодировать последовательность символов БГАВ и записать результат в восьмеричном коде, то получится:
1) 175423
2) 115612
3) 62577
4)
|
Дано: А = 10002 Б: 10012 в: 10102 г = 10112 |
Решение БГАВ2 = 10011011100010102 — - 1156128, что соответствует номеру ответа 2. Ответ: 1156128. |
|
Найти: БГАВ8 |
Номер ответа: 2. |
10. Для кодирования букв А, В, С, D используются последовательные трехразрядные двоичные числа, начинающиеся с 1 (от 100 до 111 соответственно). Если таким способом закодировать последовательность символов CDAB и записать результат в шестнадцатеричном коде, то получится:
1) А5216
2) 4C816
3) 15D16
4) DE516
|
Дано: А =
1002 в- 1012
|
Решение
|
|
Найти: CDAB |
Номер ответа: 4. |
К, L, М, N последовательные четырехразрядные двоичные числа от 1000 до 1011 соответственно. Если таким способом закодировать последовательность символов kMLN и записать результат в восьмеричном коде, то получится:
|
Дано: к = 10002 10012 м = 10102 |
Решение КМЫЧ = 10001010100110112 - 001000101010011011 2 — - 1052338, что соответствует номеру ответа 2. ответ: 1052338. |
|
Найти: КМЫЧ 8 — ? |
Номер ответа: 2. |
12. Для пяти букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, а для некоторых — из трех). Эти коды представлены в таблице:
|
а |
Ь |
с |
|
|
|
100 |
110 |
011 |
01 |
10 |
Определите, какой набор букв закодирован двоичной строкой 1000110110110, если известно, что все буквы в последовательности разные:
1) cbade 2) acdeb З) acbed 4) bacde
|
Дано: а = 1002 Ь= 11О2 с=011 2 d=012 е=10 2 |
Решение Закодируем предложенные наборы букв и сравним полученный результат с двоичной строкой 1000110110110.
acdeb = 1000110110110;
bacde = 1101000110110. Таким образом, правильный номер ответа—2. Ответ: acdeb. |
|
Найти: 1000110110110 — ? |
Номер ответа: 2. |
13. Для шести букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, а для некоторых — из трех). Эти коды представлены в таблице:
|
|
в |
с |
D |
Е |
|
|
|
100 |
10 |
011 |
11 |
101 |
Определите, какая последовательность из шести букв закодиро-
![]()
|
Дано: А = 10012 10102 с = 10112 D = 1100 |
Решение CADB2
10111001110010102 |
В9СА |
|
Найти: CADB 16 — ? |
Номер ответа: 4. |
|
|
Дано: А = 002 в = 1002 с, 102 D=0112 Е= 112 102 |
Решение Закодируем предложенные наборы букв и сравним полученный результат с двоич-
EFCABD = 111011000100011. Таким образом, правильный номер отве-
Ответ: DECAFB. |
|
Найти:
|
Номер ответа: З. |
14. Для кодирования букв А, В, С, D используются последовательные четырехразрядные двоичные числа, начинающиеся с 1 (от 1001 до 1100 соответственно). Если таким способом закодировать последовательность символов CADB и записать результат в шестнадцатеричном коде, то получится:
1) AF5216 2)
40816 ![]() 4) В9СА16
4) В9СА16
сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
|
|
Б |
в |
|
|
|
11 |
010 |
011 |
Если таким способом закодировать последовательность символов ВГАГБВ и записать результат в шестнадцатеричном коде, то получится:
1) CDADBC16
2) А7С416
3) 41271016
4)
|
Дано: А = 002 Б=112 в = 0102 г =0112 |
Решение
Можно сразу заметить, что результатом будет являться четырехзначное шестнадцатеричное число, поскольку количество двоичных цифр равно шестнадцати, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому варианты ответа 1 и З сразу отпадают.
ответ: 4С7А16. |
|
Найти: ВГАГБВ 16 |
Номер ответа: 4. |
16. Для кодирования сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
|
|
Б |
в |
|
|
|
11 |
010 |
011 |
Если таким способом закодировать последовательность символов ГАВБВГ и записать результат в шестнадцатеричном коде, то получится:
1) 62D316
3) 3132616
4) 6213316
|
Дано:
Б, 112 в, 0102 г =0112 |
Решение ГАВБВГ2 = 01100010110100112. Можно сразу заметить, что результатом будет являться четырехзначное шестнадцатеричное число, поскольку количество двоичных цифр равно пятнадцати, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому варианты ответа З и 4 сразу отпадают. ГАВБВГ2 = 01100010110100112 = 62D316. Ответ: 62D316. |
|
Найти: ГАВБВГ |
Номер ответа: 1. |
17. Для кодирования сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
|
|
Б |
в |
|
|
|
11 |
010 |
011 |
1) 7101316
2) DBCACD16
3) 31 А 716
4) 7А1З16
|
Дано:
Б, 112 в=0102 г =0112 |
Решение
Можно сразу заметить, что результатом будет являться четырехзначное шестнадцатеричное число, поскольку количество двоичных цифр равно шестнадцати, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому варианты ответа 1 и 2 сразу отпадают.
Ответ: 7А 131 |
|
Найти: ГБВАВГ 16 |
Номер ответа: 4. |
сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
|
|
Б |
в |
|
|
оо |
11 |
010 |
011 |
Если таким способом закодировать последовательность символов ГАВБГВ и записать результат в шестнадцатеричном коде, то получится:
1) DACBDC16
2) AD2616
3) 62131016
4)
|
Дано: А = 002 Б, 112 в = 0102 г=0112 |
Решение ГАВБГВ = 01100010110110102. Можно сразу заметить, что результатом будет являться четырехзначное шестнадцатеричное число, поскольку количество двоичных цифр равно шестнадцати, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому варианты ответа 1 и З сразу отпадают. ГАВБГВ = 01100010110110102 = 62DA16. ответ: 62DA16. |
|
Найти: ГАВБГВ16 — ? |
Номер ответа: 4. |
19. Для кодирования сообщения, состоящего только из букв А, В, С, D и Е, используется неравномерный по длине двоичный код:
|
|
в |
с |
|
|
|
000 |
11 |
01 |
001 |
10 |
Какое (только одно!) из четырех полученных сообщений было передано без ошибок и может быть декодировано?
![]()
3) 110001001001110
![]()
|
Дано: А = 000 в, 11 0=01 D = 001 Е, 10 |
Решение Декодируем предложенные сообщения.
Таким образом, правильный номер ответа — 1.
|
|
Найти: ВАГБГВ16 |
Номер ответа: 1. |
1) 0001
2) 000
4) 101
|
Дано:
Б=О1 в = 001 |
Решение При решении этой задачи следует обратить внимание на то, что сообщение, записанное с помощью неравномерного по длине кода, однозначно декодируется только в том случае, если никакой код не является началом другого, более длинного кода. Рассмотрим самый короткий код для буквы Г: 11. Он не является началом никакого уже известного кода; кроме того, ни один уже имеющийся код не является началом кода 11. Поэтому данный код является правильным ответом к задаче. Ответ: 11. |
|
Найти:
|
Номер ответа: З. |
21. Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, используется неравномерный по длине код: А = О, Б = 100, В = 101. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение закодированного сообщения на буквы?
3) 01
4)
|
Дано:
Б = 100
|
Решение При решении этой задачи следует обратить внимание на то, что сообщение, записанное с помощью неравномерного по длине кода, однозначно декодируется только в том случае, если никакой код не является началом другого, более длинного кода. Рассмотрим самый короткий код для буквы Г: 1. Он является началом кодов букв Б и В, поэтому однозначное разбиение закодированного сообщения на буквы в этом случае невозможно. Код Г = 11 не является началом никакого уже известного кода; кроме того, ни один уже имеющийся код не является началом кода 11. Поэтому данный код является правильным ответом к задаче. Ответ: 11. |
|
Найти:
|
Номер ответа: 2. |
22. Черно-белое растровое изображение кодируется построчно, начиная с левого верхнего угла и заканчивая в правом нижнем углу. При кодировании 1 обозначает черный цвет, а О — белый.

Для компактности результат записали в восьмеричной системе счисления. Выберите правильную запись кода:
1) 574148
2) 534148
3) 534128
530128
Решение
Представим растровое изображение в виде однострочной цепочки пикселей:
![]()
Далее заменим черные ячейки единицами, а белые— нулями:
![]()
![]()
Переводя полученные группы в восьмеричную систему счисления, получим запись: 53412. Номер ответа: З.
23. Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется посимвольное кодирование: А — О, Б — 11, В — 100, Г — 011. Через канал связи передается сообщение ГБАВАВГ. Закодируйте это сообщение данным кодом. Полученную двоичную последовательность переведите в восьмеричный код.
1) DBACACD8 3) 7А2З8
2) 750438 ![]()
|
Дано: А = 02 Б- 112 в = 1002 г=0112 |
Решение
Можно сразу заметить, что результатом будет являться пятизначное восьмеричное число, поскольку количество двоичных цифр равно пятнадцати, а каждые три двоичные цифры соответСТВУЮТ одной восьмеричной. Поэтому возможен только вариант ответа 2.
ответ: 750438. |
|
Найти: ГБАВАВГ8 — ? |
Номер ответа: 2. |
24. Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется посимвольное кодирование: А — 10, Б — 11, В — 110, Г — О. Через канал связи передается сообщение ВАГБААГВ. Закодируйте это сообщение данным кодом. Полученную двоичную последовательность переведите в шестнадцатеричный код.
1) D3A616
2) 6203220616
3) 6A3D16
4)
|
Дано: А = 102 Б- 112 в: 1102 г = 02 |
Решение ВАГБААГВ = 11010011101001102. Можно сразу заметить, что результатом будет являться четырехзначное шестнадцатеричное число, поскольку количество двоичных цифр равно шестнадцати, а каждые четыре двоичные цифры соответствуют одной шестнадцатеричной. Поэтому варианты ответа 2 и 4 сразу отпадают. ВАГБААГВ2 = 11010011101001102 = D3A616, что соответствует номеру ответа 1. Ответ: D3A616. |
|
Найти: ВАГБААГВ16 — |
Номер ответа: 1. |
Единицы измерения количества информации.
1. В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение промежуточного финиша каждым из участников, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством после того, как промежуточный финиш прошли 70 велосипедистов?
1) 70 бит
2) 70 байт
З) 490 бит
119 байт
|
Дано: N= 119 к = 70 |
Решение Для регистрации номера каждого из 119 спортсменов необходимо 7 бит, поскольку с помощью 7 бит можно представить 2 7 = 128 различных номеров (т. е. 6 бит будет недостаточно). Таким образом, i = 7 бит. Воспользовавшись формулой I = К • i, получим: 70 490 (бит). Ответ: информационный объем искомого сообщения авен 490 бит. |
|
Найти:
|
Номер ответа: З. |
1) 240 байт 2) ЗОО байт З) 360 байт 4) 420 байт
|
Дано: к = 60 |
Решение Для записи одного символа автомобильного номера необходимо i = 5 бит, поскольку с помощью 5 бит можно представить 2 5 = 32 Раз-ЛйЧНЫХ букв и десятичных цифр (т. е. 4 бит будет недостаточно). Следовательно, для
кодирования автомобильного номера, состоящего из 7 символов, нужно 7 • i = 35
бит. Однако в условии задачи указано, что каждый номер в компьютерной
программе записывается минимально возможным и одинаковым целым количеством
байт. Значит, для кодирования одного номера необходимо 5 байт, поскольку 35
бит Воспользуемся формулой: I = К • i, получим I = 60 • 5 = — ЗОО (байт). Ответ: объем памяти, отводимый этой программой для записи 60 номе ов, авен ЗОО байт. |
|
Найти: I— ? |
Номер ответа: 2. |
З. Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно быть на табло, чтобы с его помощью можно было передать 18 различных сигналов?
|
Дано:
ЛУ = 18 |
Решение Воспользуемся формулой: Следовательно, К = З, 4, 5, . Поскольку необходимо определить наименьшее количество лампочек, К = З. |
|
Найти:
|
Ответ: З. |
4. В корзине лежат 32 клубка шерсти, из них 4 красных. Сколько бит информации несет сообщение о том, что из корзины достали клубок красной шерсти?
1)
2) 2 бит 4) 4 бит
|
Дано:
п=32 |
Решение Воспользуемся формулой Шеннона: i = log», где р = п/т. Следовательно, i = log2 8 = З (бит). Ответ: З бит. |
|
Найти:
|
Номер ответа: З. |
5. Для кодирования нотной записи используется 7 значков — нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот?
1) 180 бит
2) 540 бит
З) 100 байт
1 Кбайт
|
Дано:
к = 180 |
Решение Поскольку нота кодируется одним и тем же минимально возможным количеством бит, для кодирования каждой ноты понадобится i = З бит, так как 2 (2 бит будет недостаточно). Воспользовавшись формулой I = К • i, получим: 1 = 180 • 540 (бит). Ответ: информационный объем искомого сообщения равен 540 бит. |
|
Найти:
|
Номер ответа: 2. |
6. В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что из корзины достали черный
|
Дано: i = 4 бита п = 64 |
Решение Воспользуемся формулой Шеннона: i = logo, где р = п / т. Следовательно, i = 10g2 64 / т = 4 (бит), значит, т = 4. Ответ: в коробке было 4 белых карандаша. |
|
Найти:
|
Номер ответа: 4. |
|
Дано: т = 24 |
Решение Общее количество шаров, лежащих в корзине, равно: К = 8 + 24 = 32 (шара). Воспользуемся формулой Шеннона: i = log,-zp, где р = К/п. Следовательно, i = log2 4 = 2 (бит) Ответ: 2 бит. |
|
Найти:
|
Номер ответа: 2. |
7. В коробке лежат 64 цветных карандаша. Сообщение о том, что из коробки достали белый карандаш, несет 4 бит информации. Сколько белых карандашей было в коробке?
![]()
8. В корзине лежат черные и белые шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?
2) 24
3) 36
4) 48
|
Дано: i = 2 бита т = 18 |
Решение Воспользуемся формулой Шеннона: i = log2 р, где р = п/т, причем п — общее количество карандашей и п = т + К. Следовательно, р = (т + КУК. Отсюда: i = log2 (т +
Ь)/К = 2 (бита), значит, (т + К)/К = 4 (18 + Тогда п = 18 + 6 = 24 (шара) было всего в корзине. Ответ: в корзине было 24 шара. |
|
Найти:
|
Номер ответа: 2. |
9. В закрытом ящике лежат 32 карандаша, некоторые из них — синего цвета. Наугад вынимается один карандаш. Сообщение «этот карандаш — НЕ синий» несет 4 бит информации. Сколько синих карандашей в ящике?
2) 24
3) зо
4) 32
|
Дано: i = 4 бита п, 32 |
Решение Воспользуемся формулой Шеннона: i = log,zp, где р = п/т. Следовательно, i = log2 32/m = 4 (бит), значит, т = 2. Тогда К = п — т К = 32 — 2 = 30 (карандашей) —синих. Ответ: в ящике 30 синих карандашей. |
|
Найти:
|
Номер ответа: З. |
10. Некоторый алфавит содержит четыре различных символа. Сколько трехбуквенных слов можно составить из символов этого алфавита, если символы в слове могут повторяться?
|
Дано:
|
Решение Воспользуемся формулой: mk =N 4 3 =N. Следовательно, ЛТ = 64. Ответ: из имеющегося алфавита можно составить 64 трехбуквенных слова. |
|
Найти: N—? |
Номер ответа: З. |
11. В некоторой стране автомобильный номер длиной 6 символов составляется из заглавных букв (всего используется 12 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер — одинаковым и минимально возможным количеством байт. Определите объем памяти, необходимый для хранения 32 автомобильных номеров.
1) 192 байта 2) 128 байт З) 120 байт 4) 32 байта
|
Дано: N=22 к , 32 |
Решение Для записи одного символа автомобильного номера необходимо i = 5 бит, поскольку с помощью 5 бит можно представить 2 5 = 32 различных букв и десятичных цифр (4 бит будет недостаточно). Следовательно, для кодирования автомобильного номера, состоящего из 6 символов, нужно 6 • i = 30 (бит). Однако в условии задачи сказано, что каждый номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт. Значит, для кодирования одного символа необходимо 4 байта, поскольку 30 бит 4 байта (З байт недостаточно). Воспользуемся формулой I = К • i. Получим: I = 32 • 4 = 128 (байт). Ответ: объем памяти, необходимый для записи 32 автомобильных номе ов, авен 128 байт. |
|
Найти: I—? |
Номер ответа: 2. |
12. В некоторой стране автомобильный номер длиной 5 символов составляется из заглавных букв (всего используется 30 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер — одинаковым и минимально возможным количеством байтов. Определите объем памяти, необходимый для хранения 50 автомобильных номеров.
1) 100 байт
2) 150 байт
3) 200 байт
4)
|
Дано:
к = 50 |
Решение Для записи одного символа автомобильного номера необходимо i = 6 бит, поскольку с помощью 6 бит можно представить 2 6 = 64 различных букв и десятичных цифр (5 бит будет недостаточно). Следовательно, для
кодирования автомобильного номера, состоящего из 5 символов, нужно 5 • i = 30
(бит). Однако в условии задачи сказано, что каждый номер в компьютерной
программе записывается минимально возможным и одинаковым целым количеством
байт. Значит, для кодирования одного символа необходимо 4 байта, поскольку 30
бит Воспользуемся формулой: I = К • i. Получим: I = 50 • 4 = 200 (байт). Ответ: объем памяти, необходимый для записи 50 автомобильных номеров, равен 200 байт. |
|
Найти: I — ? |
Номер ответа: З. |
13. Световое табло состоит из светящихся элементов, каждый из которых может гореть одним из трех различных цветов. Сколько различных сигналов можно передать с помощью табло, состоящего из четырех таких элементов (при условии, что все элементы должны гореть)?
2) 16
3) 64
|
Дано:
|
Решение Воспользуемся формулой: т к = 3 4 = Следовательно, = 81. Ответ: с помощью светового табло можно передать 81 различный сигнал. |
|
Найти:
|
Номер ответа: 1. |
1) 120 байт
2) 160 байт
З) 200 байт
4) 240 байт
|
Дано:
к = 40 |
Решение Для записи одного символа автомобильного номера необходимо 5 бит, поскольку с помощью i = 5 бит можно представить 25 — 32 различных букв и десятичных цифр (4 бит будет недостаточно). Следовательно, для кодирования автомобильного номера, состоящего из 6 символов, нужно 6 • i = 30 (бит). Однако в условии задачи сказано, что каждый номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт. Значит, для кодирования одного символа необходимо 4 байта, поскольку 30 бит 4 байта (З байт недостаточно). Воспользуемся формулой: I = К • i. Получим: I = 40 • 4 = 160 (байт). Ответ: объем памяти, необходимый для записи 40 автомобильных номеров, равен 160 байт. |
|
Найти: I — ? |
Номер ответа: 2. |
15. В некоторой стране автомобильный номер длиной 6 символов составляется из заглавных букв (всего используется 26 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер — одинаковым и минимально возможным количеством байт. Определите объем памяти, необходимый для хранения 20 автомобильных номеров.
|
Дано:
к = 20 |
Решение Для записи одного символа автомобильного номера необходимо i = 6 бит, поскольку с помощью 6 бит можно представить 2 6 = 64 различных букв и десятичных цифр (5 бит будет недостаточно). Следовательно, для кодирования автомобильного номера, состоящего из 6 символов, нужно 6 • i = 36 (бит). Однако в условии задачи сказано, что каждый номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт. Значит, для кодирования одного символа необходимо 5 байт, поскольку 36 бит 5 байт (4 байт недостаточно). Воспользуемся формулой: I = К • i. Получим: I = 20 • 5 = 100 (байт). Ответ: объем памяти, необходимый для записи 20 автомобильных номеров, равен 100 байт. |
|
Найти: I— ? |
Номер ответа: З. |
16. Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность флагов важна!). Какое количество различных сигналов может передать корабль при помощи четырех сигнальных флагов, если на корабле имеются флаги трех различных видов (флагов каждого вида — неограниченное количество)?
|
Дано:
|
Решение Воспользуемся формулой: т к = 3 4 = № Следовательно, N = 81. |
|
Найти: |
Ответ: 81. |
17. Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность флагов важна!). Какое количество различных сигналов может передать корабль при помощи пяти сигнальных флагов, если на корабле имеются флаги четырех различных видов (флагов каждого вида — неограниченное количество)?
|
Дано:
|
Решение Воспользуемся формулой: тк = 4 5 = М Следовательно, лт = 1024. |
|
Найти:
|
Ответ: 1024. |
18.
|
Дано: ДТ = 678 к = 200 |
Решение Для регистрации номера каждого из 678 спортсменов необходимо 10 бит, поскольку с помощью 10 бит можно представить 2 10 = 1024 различных номера (9 бит для этого будет недостаточно). Таким образом, i = 10 бит. Воспользовавшись формулой I = К • i, получим:
Ответ: информационный объем искомого сообщения равен 250 байт. |
|
Найти:
|
Ответ: 250. |
19. Некоторое сигнальное устройство за одну секунду передает один из трех сигналов. Сколько различных сообщений длиной в четыре секунды можно передать при помощи этого устройства?
|
Дано:
|
Решение Воспользуемся формулой: пе = лт 3 4 =N. Следовательно, лт = 81. |
|
Найти: N—? |
Ответ: 81. |
20.
|
Дано:
|
Решение Для записи одного номера года необходимо i1 = 12 бит, поскольку с помощью 12 бит можно представить 212 = 4096 различных чисел (11 бит будет недостаточно). Для записи одного месяца необходимо i2 = 4 бит, поскольку с помощью 4 бит можно представить 24 = 16 различных чисел (З бит будет недостаточно). Для записи одного дня в месяце необходимо i3 = 12 бит, поскольку с помощью 5 бит можно представить 2 5 = 32 различных числа (4 бит будет недостаточно). Значит, для кодирования всей записи необходимо |
|
Найти:
|
Ответ: 21. |
21. Вася и Петя передают друг другу сообщения, используя синий, красный и зеленый фонарики. Это они делают, включая по одному фонарику на одинаковое короткое время в некоторой последовательности. Количество вспышек в одном сообщении — З или 4, между сообщениями делаются паузы. Сколько различных сообщений могут передавать мальчики?
зо
![]()
|
Дано:
|
Решение Воспользуемся формулой:
3 4 = N, следовательно, N1 = 81. 3 3 = дт , следовательно, N2 = 27. N=N1 +N2 |
|
Найти:
|
Ответ: 108. |
22. Для кодирования ЗОО различных сообщений используются 5 последовательных цветовых вспышек. Вспышки имеют одинаковую длительность, при этом для каждой вспышки используется одна лампочка определенного цвета. Лампочки скольких цветов должны использоваться при передаче (укажите минимально возможное их количество)?
|
Дано: ЛТ = зоо |
Решение Воспользуемся формулой: т к = N т 5 = ЗОО. Следовательно, т = 4 (З цветов будет недостаточно). |
|
Найти:
|
Ответ: 4. |
23. Учитель, выставляя в журнал оценки по биологии за третью четверть (З, 4 или 5), обратил внимание, что комбинация из трех таких оценок по этому предмету у всех учеников различна. Каким может быть максимальное количество учеников в этом классе?
|
Дано:
к=з |
Решение Воспользуемся формулой: т к = 3 3 = Следовательно, лт = 27. |
|
Найти:
|
Ответ: 27. |
![]()
24. Некоторый алфавит содержит четыре различных символа. Сколько слов длиной ровно в 4 символа можно составить из символов данного алфавита (символы в слове могут повторяться)?
|
Дано:
|
Решение Воспользуемся формулой: = 4 4 = Следовательно, лт = 256. |
|
Найти: N—? |
Ответ: 256. |
25. Квадратное световое табло 2 х 2 состоит из светящихся элементов, каждый из которых может гореть одним из четырех различных цветов. Сколько различных сигналов можно передать с помощью табло, состоящего из четырех таких элементов (при условии, что все элементы должны гореть)?
|
Дано:
|
Решение Воспользуемся формулой:
Следовательно, = 256. |
|
Найти:
|
Ответ: 256. |
26. Световое табло состоит из светящихся элементов, каждый из которых может гореть одним из восьми различных цветов. Сколько различных сигналов можно передать с помощью табло, состоящего из трех таких элементов (при условии, что все элементы должны гореть)?
|
Дано:
|
Решение Воспользуемся формулой: = 8 3 = Следовательно, N = 512. |
|
Найти: N—? |
Ответ: 512. |
32
Скорость передачи информации
1. У Васи есть доступ к Интернету по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения информации 256 Кбит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 32 Кбит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 5 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу.
Компьютер Васи может начать ретрансляцию данных не раньше, чем получит первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах) с момента начала скачивания данных Васей и до полного их получения Петей?
(В ответе надо указать только число; слово «секунд» или букву
«с» добавлять не нужно.)
|
Дано:
!..'2 = 32 Кбит/с I = 5 Мбайт I1 = 512 Кбайт |
Решение
= 32 Кбит/с = 2 5 Кбит/с. I = 5 Мбайт = 5 • 2 10 Кбайт = 5 • 2 13 Кбит. = 512 Кбайт = 2 9 Кбайт = 2 1[1] Кбит. Воспользуемся формулой:
t1 = I1/V1 t1 = 2 12 /2 8 = 2 4 = 16 (с) — время, которое затратит Вася на получение первых 512 Кбайт данных.
время, которое затратит Петя на скачивание 5 Мбайт данных. t=t1 +t2 16 + 1280= 1296 |
|
Найти:
|
Ответ: 1296. |
|
Дано:
I = 625 Кбайт |
Решение и = 128 ООО бит/с = 125 • 2 10 бит. 1 = 625 Кбайт = 625 • 2 10 байт = 625 • 2 13 бит. Воспользуемся формулой:
|
|
Найти:
|
Ответ: 40. |
|
Дано: и = 512 ООО бит/с t = 1 мин |
Решение о = 512 ООО бит/с = 125 • 2 12 бит, t= 1 мин = 60 с. Воспользуемся формулой:
|
|
Найти:
|
Ответ: 3750. |
4. Скорость передачи данных через это соединение равна 1 024 ООО бит/с. Передача файла через это соединение заняла 5 секунд. Определите размер файла в килобайтах.
|
Дано: о = 1 024 ООО бит/с t= 5 c |
Решение
Воспользуемся формулой:
= 625 (Кбайт) — размер файла. |
|
Найти: I—? |
Ответ: 625. |
2 ДергачеваЛ. М.
5. Скорость передачи данных через АТЫ-,-соединение равна 256 ООО бит/с. Передача файла через это соединение заняла 2 минуты. Определите размер файла в килобайтах.
|
Дано: и = 256 ООО бит/с t = 2 мин |
Решение о = 256 ООО бит/с = 125 • 2 11 бит, t= 2 мин = 120 с. Воспользуемся формулой:
= 1875 • 2 14 = 3750 • 2 13 (бит) = 3750 (Кбайт) — размер файла. |
|
Найти: |
ответ: 3750. |
6.
|
Дано: 28 800 бит/с т = 640 п = 480
|
Решение З байта = 24 бита. Определим объем растрового изображения: Воспользуемся формулой:
|
|
Найти: |
Ответ: 256. |
7. Скорость передачи данных через модемное соединение равна 51 200 бит/с. Передача текстового файла через это соединение заняла 10 с. Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.
|
Дано: v = 51 200 бит/с i= 16 бит |
Решение Воспользуемся формулой: —1= 51 200 • 512 000 (бит). Найдем количество символов, содержащихся в тексте: k=I/i гэ К = 512 ООО / 16 = 32 ООО (символов). |
|
Найти: |
Ответ: 32 ООО. |
8.
|
Дано: о = 128 ООО бит/с t = 1 мин = 16 бит |
Решение
Воспользуемся формулой:
Найдем количество символов, содержащихся в тексте:
|
|
Найти:
|
Ответ: 480 ООО. |
9. Информационное сообщение объемом 2,5 Кбайт передается со скоростью 2560 бит/мин. За сколько минут будет передано данное сообщение?
|
Дано:
I = 2,5 Кбайт |
Решение I = 2,5 Кбайт = 2,5 • 2 10 байт = 2,5 • 2 13 бит. Воспользуемся формулой: t=I/v t=2,5 • 2 13 /2560=8 (мин) — время передачи файла. |
|
Найти:
|
Ответ: 8. |
10.
|
Дано:
16 бит т = 400 |
Решение t= 1,5 мин = 90 с. Воспользуемся формулой: Найдем количество символов, содержащихся в тексте: К = I/i К = 691 200/16 = 43 200 (символов). Поскольку на одной странице содержится 400 символов, получаем: s = К/т s = 43 200/400 = 108 (страниц). |
|
Найти:
|
Ответ: 108. |
11. Средняя скорость передачи данных с помощью модема равна
36 864 бит/с. Сколько секунд понадобится модему, чтобы передать 4 страницы текста в 8-битной кодировке КОИ8, если считать, что на каждой странице в среднем содержится 2304 символа?
|
Дано:
К = 2304 символа |
Решение Определим размер передаваемого файла:
|
|
Найти:
|
Ответ: 2. |
12. Скорость передачи данных через модемное соединение равна
4096 бит/с. Передача текстового файла через это соединение заняла 10 с. Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.
|
Дано: v = 4096 бит/с
|
Решение Воспользуемся формулой:
Найдем количество символов, содержащихся в тексте: К = I/i К = 40 960/16 = 2560 (символов). |
|
Найти:
|
Ответ: 2560. |
13. Передача данных через АТМ.-соединение заняла 2 минуты. За это время был передан файл, размер которого равен 3750 Кбайт. Определите минимальную скорость (бит/с), при которой возможна такая передача.
|
Дано: t = 2 мин = 3750 Кбайт |
Решение t= 2 мин = 120 с = 3750 Кбайт = 3750 2 13 (бит). Воспользуемся формулой: v=I/t 3750 • 2 13 /120 = 256 000 (бит/с). |
|
Найти:
|
Ответ: 256 ООО. |
14.
|
Дано:
I = 225 Кбайт |
Решение = 225 Кбайт = 225 • 2 10 байт — -225 • 2 13 (бит). Воспользуемся формулой:
|
|
Найти:
|
Ответ: 128. |
15. Сколько секунд потребуется модему, передающему сообщения со скоростью 28 800 бит/с, чтобы передать 100 страниц текста в 30 строк по 60 символов каждая при условии, что каждый символ кодируется одним байтом?
|
Дано: = 28 800 бит/с s = 100 страниц i = 1 байт st = 30 строк .sm = 60 символов |
Решение i= 1 байт = 8 бит. Определим размер передаваемого файла:
— 1 440 ООО (бит). Воспользуемся формулой:
|
|
Найти:
|
Ответ: 50. |
16.
|
Дано:
|
Решение
Воспользуемся формулой:
|
|
Найти: I—? |
Ответ: 2400. |
17. Скорость передачи данных через АТМ.-соединение равна 128 ООО бит/с. Сколько времени (в секундах) займет передача по этому каналу файла объемом 500 Кбайт?
|
Дано: v = 128 ООО бит/с = 500 Кбайт |
Решение I = 500 Кбайт = 500 • 2 10 байт = 500 • 2 13 (бит). Воспользуемся формулой:
|
|
Найти:
|
Ответ: 32. |
![]()
512 ООО Передача файла по этому каналу занимает 16 с. Определите объем файла в килобайтах.
|
Дано: о = 512 ООО бит/с
|
Решение Воспользуемся формулой:
= 1000 (Кбайт) — размер файла. |
|
Найти:
|
Ответ: 1000. |
|
Дано:
120 с |
Решение Воспользуемся формулой: I=v. 128 ООО • 120= 15 360 ООО (бит) = = 1875 (Кбайт) — размер файла. |
|
Найти:
|
Ответ: 1875. |
19. Через АТМ.,-соединение файл размером 2500 Кбайт передавался в течение 40 с. Сколько секунд потребуется для передачи файла размером 2750 Кбайт?
|
Дано: I = 2500 Кбайт I1 = 2750 Кбайт |
Решение I= 2500 Кбайт = 2500 • 2 13 бит, I1 = 2750 Кбайт = 2750 • 2 13 бит. Воспользуемся формулой: о = I/t и = 2500 • 2 13 /40 = 62,5 • 2 13 (бит/с) — время передачи файла. t1 |
|
Найти:
|
Ответ: 44. |
20.
Скорость передачи данных через ![]() равна
равна
128 ООО бит/с. Передача файла через данное соединение заняла 120 с. Каков объем этого файла в Кбайтах (в качестве ответа запишите только число)?
21. АТЬсоединение 64 ООО Сколько времени (в секундах) займет передача по этому каналу файла объемом 375 Кбайт?
|
Дано: v = 64 ООО бит/с = 375 Кбайт |
Решение I = 375 Кбайт = 375 • 2 10 байт = 375 • 2 13 (бит). Воспользуемся формулой:
|
|
Найти:
|
Ответ: 48. |
|
Дано: И = 128 ООО бит/с I = 625 Кбайт |
Решение
Воспользуемся формулой:
|
|
Найти:
|
Ответ: 40. |
22.
|
Дано: о = 14 400 бит/с т = 640 п = 480 i = 24 бит |
Решение Определим объем растрового изображения:
|
|
Найти:
|
Ответ: 512. |
23.
Скорость передачи данных через ![]() равна 128 ООО бит/с.
Сколько времени (в секундах) займет передача по этому каналу файла объемом 625
Кбайт?
равна 128 ООО бит/с.
Сколько времени (в секундах) займет передача по этому каналу файла объемом 625
Кбайт?
![]()
256 ООО Передача файла через данное соединение заняла 40 с. Каков объем файла в Кбайтах (в качестве ответа запишите только число)?
|
Дано:
|
Решение Воспользуемся формулой:
= 1250 (Кбайт) — размер файла. |
|
Найти: I—? |
Ответ: 1250. |
25. Сколько секунд потребуется модему, передающему сообщения со скоростью 19 200 бит/с, чтобы передать цветное растровое изображение размером 1280 х 800 пикселей при условии, что цвет каждого пикселя кодируется 24 битами?
|
Дано: и = 19 200 бит/с т = 1280 п = 800 i = 24 бит |
Решение Определим объем растрового изображения:
|
|
Найти:
|
Ответ: 1280. |
1. Между четырьмя местными аэропортами — ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО ежедневно выполняются авиарейсы. В таблице приведен фрагмент расписания перелетов между ними.
|
Аэропорт вылета |
Аэропорт прилета |
Время вылета |
Время прилета |
|
сосново |
КРАСНЫЙ |
06:20 |
08:35 |
|
КРАСНЫЙ |
ОКТЯБРЬ |
10:25 |
12:35 |
|
ОКТЯБРЬ |
КРАСНЫЙ |
|
13:30 |
|
БЕРЕГ |
сосново |
|
14:25 |
|
сосново |
ОКТЯБРЬ |
12 : |
16:35 |
|
КРАСНЫЙ |
сосново |
13:15 |
15 : |
|
ОКТЯБРЬ |
сосново |
|
17:25 |
|
ОКТЯБРЬ |
БЕРЕГ |
15:30 |
|
|
сосново |
БЕРЕГ |
17:35 |
19:30 |
|
БЕРЕГ |
ОКТЯБРЬ |
19 : 4 О |
21:55 |
Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (00:00). Определите самое раннее время, когда он может попасть в аэропорт СОСНОВО.
1) 15:40
2) 16:35
3) 17:15
4) 17:25
Решение
Проанализировав таблицу, можно сделать вывод о том, что прямой рейс ОКТЯБРЬ — СОСНОВО позволит путешественнику попасть в аэропорт самое раннее в 17:25, тогда как остальные варианты не приведут к нужному результату.
![]()
При решении этой задачи важно предотвратить ошибку,
связанную с выбором рейсов ОКТЯБРЬ — КРАСНЫЙ и КРАСНЫЙ ![]() СОСНОВО. Казалось бы,
это позволит достичь аэропорта СОСНОВО быстрее, но из таблицы видно, что
путешественнику не удастся осуЩеСТВИТЬ пересадку на второй рейс. Номер ответа:
4.
СОСНОВО. Казалось бы,
это позволит достичь аэропорта СОСНОВО быстрее, но из таблицы видно, что
путешественнику не удастся осуЩеСТВИТЬ пересадку на второй рейс. Номер ответа:
4.
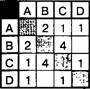
2. В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую этой таблице.

|
|
|
4 |
|
|
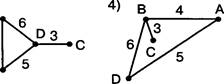
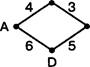 1) в 2) 5 3)
1) в 2) 5 3)
СА с6 4
в з
Решение
Проанализировав таблицу, можно сделать вывод о том, что три первые схемы не отражают полностью описанные в таблице взаимосвязи между соседними железнодорожными станциями. Например, первая схема не отражает взаимосвязь между станциями В и 1), вторая схема неправильно отражает взаимосвязь между станциями В и С, а третья схема неправильно отражает взаимосвязь между станциями А и 1). Таким образом, таблице соответствует только схема 4. Номер ответа: 4.
З. В таблицах указана протяженность автомагистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не соединены автомагистралями. Укажите номер таблицы, для которой выполняется условие: «Максимальная протяженность маршрута от пункта А до пункта С не больше 5». (Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами. При этом любой населенный пункт должен встречаться на маршруте не более одного раза.)
![]()
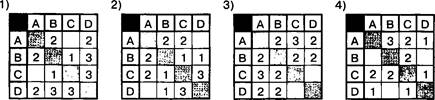
Решение
Рассмотрим возможные маршруты от пункта А до пункта С, имеющие максимальную протяженность. Проанализируем таблицу 1:

Из нее видно, что максимальная протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до 1), от D до В и от В до С: 2 + З + 1 = 6. Однако этот результат не удовлетворяет условию задачи.
Проанализируем таблицу 2:

Из нее видно, что максимальная протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до В, от В до D и от D до С: 2 + 1 + З = 6. Этот результат тоже не удовлетворяет условию задачи.
Проанализируем таблицу З:

Из нее видно, что максимальная протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до D, от D до В и от В до С: 2 + 2 + 2 = 6. Этот результат также не удовлетворяет условию задачи.
![]()
Наконец, проанализируем таблицу 4:

Из нее видно, что максимальная протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до Е), от D до С: 1 + 1 = 2. Также в этом случае возможен прямой маршрут от пункта А до пункта С, равный по длине 2. Оба этих результата полностью удовлетворяют условию задачи. Номер ответа: 4.
4. В таблице указана стоимость перевозки грузов между соседними станциями. Если пересечение строки и столбца пусто, то соответствующие станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость перевозки грузов от пункта А до пункта В не больше З».
1) 2) 3) 4)
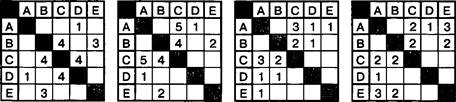
Решение
Рассмотрим возможные маршруты от пункта А до пункта В и будем искать минимальную стоимость перевозки грузов, не превышающую З.
Проанализируем таблицу 1 :

Из нее видно, что перевозка грузов не может быть осуществлена напрямую и стоимость маршрута от пункта А до пункта В равна сумме стоимостей маршрутов от А до 1), от D до С и от С до В: 1 + 4 + 4 = 9. Однако данный результат не удовлетворяет условию задачи.
46
![]()
Проанализируем таблицу 2:

Из нее видно, что перевозка грузов не может быть осуществлена напрямую и стоимость маршрута от пункта А до пункта В равна сумме стоимостей маршрутов от А до С и от С до В: 5 + 4 = 9. Данный результат также не удовлетворяет условию задачи. Проанализируем таблицу З:
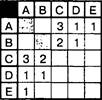
Из нее видно, что и здесь перевозка грузов не может быть осуществлена напрямую и стоимость маршрута от пункта А до пункта В равна сумме стоимостей маршрутов от А до D и от D до В: 1 + 1 = 2. Данный результат уже удовлетворяет условию задачи. Проанализируем таблицу 4:
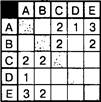
Из нее видно, что перевозка грузов не может быть осуществлена напрямую и стоимость маршрута от пункта А до пункта В есть сумма стоимостей маршрутов от А до С и от С до В: 2 + 2 = 4. Данный результат не удовлетворяет условию задачи. Номер ответа: З.
5. В таблице указана стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую этой таблице.
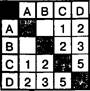

Решение
Проанализировав таблицу, можно сделать вывод, что первая схема соответствует стоимости перевозки пассажиров между соседними населенными пунктами, а остальные схемы не соответствуют ей. Например, вторая схема неправильно отражает взаимосвязь между населенными пунктами А и С, третья схема не отражает взаимосвязь между населенными пунктами В и С, а четвертая схема не отражает взаимосвязь между населенными пунктами А и С. Таким образом, таблице соответствует только схема 1.
Номер ответа: 1.
6.
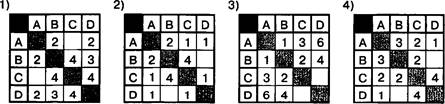
Решение
Рассмотрим возможные маршруты от пункта В до пункта D и будем искать максимальную стоимость перевозки грузов, не превышающую 6.
Проанализируем таблицу 1:

Из нее видно, что стоимость перевозки грузов от пункта В до пункта D складывается из стоимостей перевозок от В до С и от С до 1):
4 + 4 = 8. Этот результат не удовлетворяет условию задачи. Проанализируем таблицу 2:
Из нее видно, что стоимость перевозки грузов от пункта В до пункта D складывается из стоимостей перевозок от В до С и от С до 1):

Из нее видно, что стоимость перевозки грузов от пункта В до пункта D складывается из стоимостей перевозок от В до С, от С до А и от А до D: 2 + З + 6 = 11. Такой результат не удовлетворяет условию задачи.
Проанализируем таблицу 4:

Из нее видно, что стоимость перевозки грузов от пункта В до пункта D складывается из стоимостей перевозок от В до А, от А до С и от С до 1): З + 2 + 4 = 9. Этот результат не удовлетворяет условию задачи. Номер ответа: 2.
7. В таблице указана стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую этой таблице.


Решение
8. В таблицах указана протяженность автомагистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не являются соседними. Укажите номер таблицы, для которой выполняется условие: «Максимальная протяженность маршрута от пункта А до пункта С не больше 6» . (Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами. При этом через любой населенный пункт маршрут должен проходить не более одного раза.)
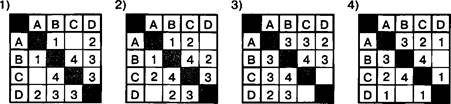
Решение
Рассмотрим возможные маршруты от пункта А до пункта С и будем искать максимальную протяженность маршрута, нё превышающую 6.
Проанализируем таблицу 1:

Из нее видно, что протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до 1), от D до В и от В до С:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•апз• |
||||
|
|
|
|
|
|
Из нее видно, что протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до В, от В до D и от D до С:
1 + 2 + З = 6. Этот результат удовлетворяет условию задачи. Проанализируем таблицу З:

Из нее видно, что протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до 1), от D до В и от В до С:
2 + З + 4 = 9. Этот результат не удовлетворяет условию задачи. Проанализируем таблицу 4:

Из нее видно, что протяженность маршрута от пункта А до пункта С есть сумма длин маршрутов от А до В и от В до С: З + 4 — 7. Этот результат тоже не удовлетворяет условию задачи. Номер ответа: 2.
9. В таблице указана стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую этой таблице.

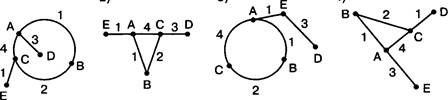
Решение
Проанализировав таблицу, можно сделать вывод, что вторая схема соответствует стоимости перевозки пассажиров между соседними населенными пунктами, а остальные схемы не соответствуют ей. Например, первая схема содержит взаимосвязь между населенными пунктами С и Е, которой нет в таблице, третья схема не отраэкает взаимосвязь между населенными пунктами С и 1), а четвертая схема неправильно отражает взаимосвязь между населенными пунктами А и Е. Таким образом, таблице соответствует только схема 2. Номер ответа: 2.
10. В таблице указана стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую этой таблице.

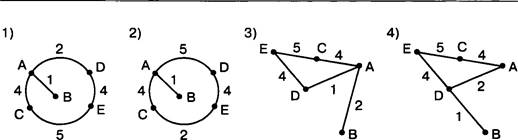
Решение
Проанализировав таблицу, можно сделать вывод, что третья схема соответствует стоимости перевозки пассажиров между соседними населенными пунктами, а остальные схемы не соответствуют ей. Например, первая схема неправильно отражает взаимосвязь между населенными пунктами А и В, вторая схема неправильно отражает взаимосвязь между населенными пунктами А и 1), а четвертая схема не отражает взаимосвязь между населенными пунктами А и В. Таким образом, таблице соответствует только схема З. Номер ответа: З.
11. Путешественник пришел в 08:00 на автостанцию поселка ЛЕСНОЕ и увидел следующее расписание автобусов.
|
Отправление из |
Прибытие в |
Время отправления |
Время прибытия |
|
ЛЕСНОЕ |
ОЗЕРНОЕ |
07:45 |
08:55 |
|
ЛУГОВОЕ |
ЛЕСНОЕ |
08:00 |
09:10 |
|
ПОЛЕВОЕ |
ЛЕСНОЕ |
08:55 |
11:25 |
|
ПОЛЕВОЕ |
ЛУГОВОЕ |
09:10 |
10:10 |
|
ЛЕСНОЕ |
ПОЛЕВОЕ |
09:15 |
|
|
ОЗЕРНОЕ |
ПОЛЕВОЕ |
09:15 |
10:30 |
|
ЛЕСНОЕ |
ЛУГОВОЕ |
09:20 |
10:30 |
|
ОЗЕРНОЕ |
ЛЕСНОЕ |
09:25 |
10:35 |
|
ЛУГОВОЕ |
ПОЛЕВОЕ |
|
11:40 |
|
ПОЛЕВОЕ |
ОЗЕРНОЕ |
10:45 |
12:00 |
Определите самое раннее время, когда путешественник сможет оказаться в пункте ПОЛЕВОЕ согласно этому расписанию.
1) 10:30 3) 11:40
2) 11:25 4) 11:45
Решение
Проанализировав таблицу, можно сделать вывод, что рейсы ЛЕСНОЕ — ЛУГОВОЕ и ЛУГОВОЕ — ПОЛЕВОЕ приведут к нужному результату. Это позволит путешественнику попасть в пункт ПОЛЕВОЕ самое раннее в 11:40, тогда как остальные варианты не приведут к нужному результату. Номер ответа: З.
12.
|
Отправление из |
Прибытие в |
Время отправления |
Время прибытия |
|
КАМЫШИ |
КАЛИНИНО |
08:15 |
09:10 |
|
КАЛИНИНО |
БУКОВОЕ |
09:10 |
10:15 |
|
РАКИТИНО |
КАМЫШИ |
10:00 |
11:10 |
|
РАКИТИНО |
КАЛИНИНО |
10:05 |
12:25 |
|
РАКИТИНО |
БУКОВОЕ |
10:10 |
11:15 |
|
КАЛИНИНО |
РАКИТИНО |
10:15 |
12:35 |
|
КАЛИНИНО |
КАМЫШИ |
10:20 |
11:15 |
|
БУКОВОЕ |
КАЛИНИНО |
10:35 |
11:40 |
|
КАМЫШИ |
РАКИТИНО |
11:25 |
12:30 |
|
БУКОВОЕ |
РАКИТИНО |
11 : 40 |
12 : 40 |
Определите самое раннее время, когда путешественник сможет оказаться в пункте РАКИТИНО согласно этому расписанию.
1) 12:25
2) 12:30
3) 12:35
![]()
Решение
Проанализировав таблицу, можно сделать вывод, что прямой рейс КАЛИНИНО — РАКИТИНО позволит путешественнику попасть в нужный пункт в 12:35. Однако выбор рейсов КАЛИНИНО — КАМЫШИ, КАМЫШИ — РАКИТИНО позволит достичь пункта РАКИТИНО быстрее — в 12:30 (из таблицы видно, что путешественнику удастся осуществить пересадку на второй из этих рейсов по окончании первого).
Номер ответа: 2.
13. В таблицах указана протяженность автомагистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не являются соседними. Укажите номер таблицы, для которой выполняется условие: «Максимальная протяженность маршрута от пункта С до пункта В не больше 6». (Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами. При этом через любой населенный пункт маршрут должен проходить не более одного раза.)
1 ) 2) 3) 4)
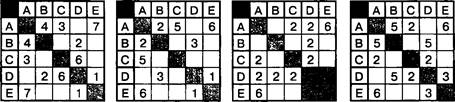
Решение
Рассмотрим возможные маршруты от пункта С до пункта В и будем искать максимальную протяженность маршрута, не превышающую 6.

Из нее видно, что протяженность маршрута от пункта С до пункта В есть сумма длин маршрутов от С до D, от D до Е, от Е до А и от А до В: б + 1 + 7 + 4 = 18. Этот результат не удовлетворяет условию задачи. Проанализируем таблицу 2:

Из нее видно, что протяженность маршрута от пункта С до пункта В есть сумма длин маршрутов от С до А, от А до Е, от Е до D и от D до В: 5 + 6 + 1 + З — 15. Этот результат тоже не удовлетворяет условию задачи.
Проанализируем таблицу З:

Из нее видно, что протяженность маршрута от пункта С до пункта В есть сумма длин маршрутов от С до А, от А до D и от D до В:
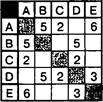
Из нее видно, что протяженность маршрута от пункта С до пункта В есть сумма длин маршрутов от С до А, от А до Е, от Е до D и от D до В: 2 + 6 + З + 5 = 16. Этот результат не удовлетворяет условию задачи.
Номер ответа: З.
14. Между четырьмя местными аэропортами ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА — ежедневно выполняются авиарейсы.
В таблице приведен фрагмент расписания перелетов между ними.
|
Аэропорт вылета |
Аэропорт прилета |
Время вылета |
Время прилета |
|
ВОСТОРГ |
ГОРКА |
13:10 |
|
|
ОЗЕРНЫЙ |
ЗАРЯ |
13:00 |
14:30 |
|
ОЗЕРНЫЙ |
ВОСТОРГ |
12:10 |
14:20 |
|
ГОРКА |
ОЗЕРНЫЙ |
11:15 |
15:30 |
|
ВОСТОРГ |
ОЗЕРНЫЙ |
12:35 |
14:50 |
|
ЗАРЯ |
ОЗЕРНЫЙ |
12:30 |
14:20 |
|
ВОСТОРГ |
ЗАРЯ |
10:30 |
12:15 |
|
ЗАРЯ |
ГОРКА |
14 : 4 О |
: 45 |
|
ГОРКА |
ЗАРЯ |
15:15 |
17:20 |
|
ОЗЕРНЫЙ |
ГОРКА |
14:30 |
16:20 |
Путешественник оказался в аэропорту ВОСТОРГ в полночь (00:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.
1) 13:10
2) 16:20
3) 16:45
4)
Решение
Проанализировав таблицу, можно сделать вывод, что рейсы ВОСТОРГ — ОЗЕРНЫЙ и ОЗЕРНЫЙ — ГОРКА позволят путешественнику попасть в аэропорт самое раннее в 16:20, тогда как остальные варианты не приведут к нужному результату. Номер ответа: 2.
1. Дано: а = 1)716, Ь = 3318. Какое из чисел с, записанных в двоичной системе, отвечает условию: а < с < Ь?
1) 11011001 3) 11010111
2) 11011100 4) 11011000
|
Дано: a=D716 Ь = 3318 a<c<b |
Решение Нужно воспользоваться правилами перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: = 11012, 716 = 01112 D716 = 110101112; 38 = 0112, 18 = 3318 = 0110110012 = 110110012. Таким образом, 110101112 < 110110012. Данному интервалу принадлежит только число 110110002. Ответ: 110110002. |
|
Найти: |
Номер ответа: 4. |
2. Как представлено число 8310 в двоичной системе счисления?
1) 10010112 3) 10100112
2) 11001012 4) 1010012
|
Дано: а = 8310 |
Решение Представим число а в развернутой форме: 8310
— 64 + 16 + 2 + 1 = 1 • 26 +0 • 2 5 1 • 24 +
О • 2 3 + + о , 2 2 +1 |
|
Найти: |
Номер ответа: З. |
![]()
З. Сколько единиц содержится в двоичной записи числа 195?
![]()
|
Дано: а = 19510 |
Решение Представим число а в развернутой форме:
+ 0, 24 Следовательно, в двоичной записи числа 195 содержатся четыре единицы. Ответ: 4. |
|
Найти: Количество единиц |
Номер ответа: 4. |
4. Сколько единиц содержится в двоичной записи числа 173?
![]()
|
Дано:
|
Решение Представим число а в развернутой форме:
Следовательно, в двоичной записи числа 173 содержатся пять единиц. Ответ: 5. |
|
Найти: Количество единиц — ? |
Номер ответа: 2. |
5. Как число 25 представлено в двоичной системе счисления?
1) 10012
2) 110012
3) 100112
4) 110102
![]()
|
Дано: а = 2510 |
Решение Представим число а в
развернутой форме: 2510-— 16 Ответ: 110012. |
|
Найти:
|
Номер ответа: 2. |
6. Как число 82 представлено в двоичной системе счисления?
1) 10100102 3) 1001012
2) 10100112 4) 10001002
|
Дано: а = 8210 |
Решение Представим число а в развернутой форме: 8210=64 + 16 +2=1 26 + О • 2 5
+1 24 + О • 23 +0 • 2 2 + |
|
Найти:
|
Номер ответа: 1. |
7. Как число 263 представлено в восьмеричной системе счисления?
1) 3018 3) 4078
2) 6508 4) 7778
|
Дано: а = 26310 |
Решение Представим
число а в развернутой форме: 26310-4 , 64 |
|
Найти:
|
Номер ответа: З. |
8. Как число 5678 записывается в двоичной системе счисления?
1) 10111012
2) 1001101112
3) 1011101112
![]()
![]()
|
Дано: а = 5678 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 8 и 2: 1012, 1102, 78 = 1112 5678= 1011101112. Ответ: 101110111. |
|
Найти:
|
Номер ответа: З. |
9. Как число А8716 записывается в восьмеричной системе счисления?
1) 4358 2) 15778 3) 52078 4) 64008
|
Дано: а = А8716 |
Решение Используем правила перевода целых чисел
между системами счисления с основаниями 16 и 2: 10102, 1000 2,
716 = Используем правила перевода целых чисел между системами счисления с основаниями 2 и 8: 1010100001112 = 52078. Ответ: 52078. |
|
Найти:
|
Номер ответа: З. |
10. Как число 7548 записывается в шестнадцатеричной системе счисления?
1) 73816 ![]() 3) 1ЕС16 4)
А5616
3) 1ЕС16 4)
А5616
|
Дано: а = 7548 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 8 и 2:
Используем правила перевода целых чисел между системами счисления с основаниями 2 и 16:
ответ: 1ЕС16. |
|
Найти: С 16 _ |
Номер ответа: З. |
9D16 , 2378.
<
|
Дано: a=F716 ь = 3718 a<c<b |
Решение Следует воспользоваться правилами перевода целых чисел из системы счисления с основанием 16 (8) в систему счисления с основанием 2:
Данному интервалу принадлежит только число
|
|
Найти:
|
Номер ответа: 4. |

|
Дано:
ь = 2378
|
Решение Следует воспользоваться правилами перевода целых чисел из системы счисления с основанием 16 (8) в систему счисления с основанием 2:
Данному интервалу принадлежит только число
|
|
Найти:
|
Номер ответа: 2. |
12. Дано: а = Р 716, Ь = 3718. Какое из чисел с, записанных в двоичной системе счисления, удовлетворяет неравенству: а < с < Ь?
![]()
2) 11011000
![]()
DD16, 3378.
<
|
Дано: а = ЕА16 Ь = 3548 a<c<b |
Решение Следует воспользоваться правилами перевода целых чисел из системы счисления с основанием 16 (8) в систему счисления с основанием 2: Е16= 11102, 10102 111010102; 38 = 0112, 58 = 1012, 48 = 1002 111011002. Таким образом: 111010102 < с 111011002. Данному интервалу принадлежит только число
Ответ: 111010112. |
|
Найти:
|
Номер ответа: З. |

|
Дано: а = DD16 ь = 3378
|
Решение Следует воспользоваться правилами перевода целых чисел из системы счисления с основанием 16 (8) в систему счисления с основанием 2:
Данному интервалу принадлежит только число
|
|
Найти:
|
Номер ответа: З. |
14. Дано: а = ЕА16, Ь = 3548. Какое из чисел с, записанных в двоичной системе счисления, удовлетворяет неравенству а с < Ь?
1) 11101010
2) 11101110
3) 11101011
4) 11101100
Е716, 3518.
1) 11101010 3) 11101011
|
Дано: а = 3228
a<c<b |
Решение Следует воспользоваться правилами перевода целых чисел из системы счисления с основанием 16 (8) в систему счисления с основанием 2: 38 = 0112, 28 — а = 110100102; D16= 11012, 110101002. Таким образом, 110100102 < с < 110101002. Данному интервалу принадлежит только число 110100112. ответ: 110100112. |
|
Найти:
|
Номер ответа: 1. |
2)
|
Дано: а = Е716 ь = 3518 a<c<b |
Решение Следует воспользоваться правилами перевода целых чисел из системы счисления с основанием 16 (8) в систему счисления с основанием 2:
Таким образом, 111001112 < с < 111010012. Данному интервалу принадлежит только число 111010002. ответ: 111010002. |
|
Найти:
|
Номер ответа: 2. |
16. Дано: а = 3228, Ь = D416. Какое из чисел с, записанных в двоичной системе счисления, удовлетворяет неравенству а с < Ь?
1) 11010011
2) 11001110
3) 11001010
4) 11001100
17. Сколько единиц содержится в двоичной записи числа 64?
![]()
|
Дано: а = 6410 |
Решение Представим число а в развернутой форме: — 1 2 6 +0 • 2 5 2 4 + О • 2 3 +0 • 2 2 +0 • 2 1 +0 • 2 0 — = 10000002. Следовательно, в двоичной записи числа 64 содержится одна единица. Ответ: 1. |
|
Найти:
|
Номер ответа: 1. |
18.
![]()
|
Дано: а = 12710 |
Решение Представим число а в развернутой форме: 12710=64 + 32 16 +8+4+2+1=1 2 4 + Следовательно, в двоичной записи числа 127 содержатся семь единиц. Ответ: 7. |
|
Найти:
|
Номер ответа: 4. |
19. Сколько значащих нулей содержится в двоичной записи числа 48?
![]()
|
Дано: а = 4810 |
Решение Представим число а в развернутой форме:
= 1100002. Следовательно, в двоичной записи числа 48 содержатся четыре значащих нуля. Ответ: 4. |
|
Найти:
|
Номер ответа: 4. |
20. Сколько значащих нулей содержится в двоичной записи числа 254?
|
Дано: |
Решение Представим число а в развернутой форме: 25410= 128 + 64 + 32 + 16 4 1 • 2 7 1 • 2 6 + 1 • 2 5 + Следовательно, в двоичной записи числа 254 содержится один значащий нуль. Ответ: 1. |
|
Найти:
|
Номер ответа: 1. |
21. Какое из чисел является наименьшим?
|
Дано:
Ь = 3478 с = 111001012
|
Решение Следует воспользоваться
правилами перевода целых чисел из системы счисления с основанием 16, 8, 2 в
систему счисления с основанием 10: а = - 230 Следовательно, наименьшим является число с = 111001012. Ответ: 11100101 . |
|
Найти: тах (а, |
Номер ответа: З. |
З Дергачева Л. м.
22. Какое из чисел является наибольшим?
1) 9В16
2) 2348
3) 100110102
4)
|
Дано:
2348 с = 100110102 15310 |
Решение Следует воспользоваться правилами перевода целых чисел из системы счисления с основанием 16, 8 и 2 в систему счисления с основанием 10: а = = 15510, ь = Следовательно, наибольшим является число ь = 2348. Ответ: 2348. |
|
|
Найти: тах (а, Ь, с, d) — ? |
Номер ответа: 2. |
23. В системе счисления с некоторым основанием х десятичное число 49 записывается в виде 100. Укажите это основание.
|
Дано: 4910 — |
Решение Представим оба числа в развернутой форме: 4 . 10 1 +9 , Решим полученное уравнение: .x 2 = 49, тогда х = ± 7. Поскольку основанием системы счисления не может являться отрицательное число, искомое основание равно 7. |
|
Найти:
|
Ответ: 7. |
|
Дано: 1210 - 110х |
Решение Представим оба числа в развернутой форме: 1 ' 10 1 +2 • 10 0 = 1 • х 2 + 1 • х 1 + О • х о Х 2 + Х— 12 Решим полученное уравнение:
Поскольку основанием системы счисления не может являться отрицательное число, искомое основание равно З. |
|
Найти:
|
Ответ: З. |
24.
|
Дано: 2210 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность:
Найдем все делители числа 18. Это числа 2, З, 6, 9 и 18. Основанием системы счисления не может являться число, меньшее 5, поскольку в искомой системе счисления присутствует цифра 4. Тогда все возможные основания систем счисления, в которых запись числа 22 оканчивается на 4, —6, 18. |
|
Найти:
|
Ответ: 6, 9, 18. |
25. В системе счисления с некоторым основанием х число 12 записывается в виде 110. Укажите это основание.
26.
|
Дано: 3910 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность: 39-3=36. Найдем все делители числа 36. Это числа 2, З, 4, 6, 9, 12, 18 и 36. Основанием системы счисления не может являться число, меньшее 4, поскольку в искомой системе счисления присутствует цифра З. Тогда все возможные основания систем счисления, в которых запись числа 39 оканчивается на З, — 4, 6, 9, 12, 18 и 36. |
|
Найти:
|
ответ: 4, 6, 9, 12, 18, 36. |
27. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
|
Дано: 2910 |
Найдем все делители числа 24. Это числа 2, З, 4, 6, 8, 12 и 24. Основанием системы счисления не может являться число, меньшее 6, поскольку в искомой системе счисления присутствует цифра 5. Тогда все возможные основания систем счисления, в которых запись числа 29 оканчивается на 5, —6,8, 12и24. |
|
|
Найти:
|
|
Ответ: 6, 8, 12, 24. |
28.
|
Дано: 12910 = 1004х |
Решение Представим оба числа в развернутой форме: 1 • 10 2 + 2 • 10 1 + 9 • 10 0 = 1 • 10 3 +0 х 2 + О • х 1 + + 4 • ХО— ХЗ = 125. Решим полученное уравнение: Искомое основание равно 5. |
|
Найти:
|
Ответ: 5. |
29. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
|
Дано: 4010 |
Решение Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. Определим разность: 40 36. Найдем все делители числа 36. Это числа 2, З, 4, 6, 9, 12, 18 и 36. Основанием системы счисления не может являться число, меньшее 5, поскольку в искомой СИСТеме счисления присутствует цифра 4. Тогда все возможные основания систем счисления, в которых запись числа 40 оканчивается на 4, — 6, 9, 12, 18 и 36. |
|
Найти:
|
Ответ: 6, 9, 12, 18, 36. |
30.
|
Дано: 2510 = 100х |
Решение Представим оба числа в развернутой форме: 2 • 10 1 + 5 • 10 0 = 1 • х 2 + О • хд + О хо х 2 = 25. Решим полученное уравнение:
Поскольку основанием системы счисления не может являться отрицательное число, искомое основание равно 5. |
|
Найти:
|
Ответ: 5. |
31. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на З.
|
Дано: 2710 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность:
Найдем все делители числа 24. Это числа 2, З, 4, 6, 8, 12 и 24. Основанием системы счисления не может являться число, меньшее 4, поскольку в искомой системе счисления присутствует цифра З. Тогда все основания систем счисления, в которых запись числа 27 оканчивается на З, —4, 6, 8, 12 и 24. |
|
Найти:
|
Ответ: 4, 6, 8, 12, 24. |
32.
|
Дано: [19 33110 |
Решение Переведем в шестеричную систему счисления числа границы заданного диапазона: 1910 - 316; 3310-53 6. Запишем в шестеричной системе все числа диапазона (путем прибавления 1): 316, 326, 336, 346, 356, 406, 416, 426, 436, 446, 456, 506, 516, 526, 536. Во всех записанных числах цифра З встречается 8 раз. |
|
Найти: Кол-во цифр З |
Ответ: 8. |
33, Укажите, сколько раз встречается цифра 1 в записи чисел 12, 13, 14, ..., 31 в системе счисления с основанием 5.
|
Дано: [12 ... 31110 |
Решение Переведем в пятеричную систему счисления числа границы заданного диапазона: 1210- 225; 111 5. Запишем в пятеричной системе все числа диапазона (путем прибавления 1): 225, 235, 245, 305, 315, 325, 335, 345, 405, 415, 425, 435, 445, 1005, 1015, 1025, 1035, 1045, 1105, 1115. Во всех записанных числах цифра 1 встречается 13 раз. |
|
Найти: Кол-во цифр 1 |
Ответ: 13. |
|
Дано: 12345 |
Решение 12345 = 1 Таким образом, при представлении в системе счисления с основанием 5 число 194 записывается как 12345. |
|
Найти: Х10 |
Ответ: 194. |
34.
|
Дано: 2310 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность:
Найдем все делители числа 22. Это числа 2, 11 и 22. Тогда все основания систем счисления, в которых запись числа 23 оканчивается на 1, — 2, 11 и 22. |
|
Найти:
|
Ответ: 2, 11, 22. |
35. Сколько значащих цифр содержится в записи десятичного числа 357 в системе счисления с основанием 7?
|
Дано: 35710 |
Решение 35710 = 1 7 3 + 0 , 7 2 + 2 • + 0 , 10207. Таким образом, в записи десятичного числа 357 в системе счисления с основанием 7 содержатся 4 значащие цифры. |
|
Найти: Кол-во цифр — ? |
Ответ: 4. |
36. Какое десятичное число при представлении в системе счисления с основанием 5 записывается как 12345?
37.
|
Дано: 3010 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность: зо 22. Найдем все делители числа 22. Это числа 2, 11 и 22. Основанием системы счисления не может являться число, меньшее 9, поскольку в искомой системе счисления присутствует цифра 8. Тогда все основания систем счисления, в которых запись числа 30 оканчивается на 8, — 11 и 22. |
|
Найти:
|
Ответ: 11, 22. |
38. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.
|
Дано: 3110 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность:
Найдем все делители числа 27. Это числа З, 9 и 27. Основанием системы счисления не может являться число, меньшее 5, поскольку
в искомой системе счисления присутствует цифра 4. Тогда все основания систем
счисления, в которых запись числа 31 оканчивается на 4 |
|
Найти:
|
Ответ: 9, 27. |
39.
|
Дано: 8310 = 123х |
Решение Представим оба числа в развернутой форме: 8 • 10 1 + 3 • 10 0 = 1 • х 2 х 1 хо Х 2 + 2Х — 80 = Решим полученное уравнение:
Поскольку основанием системы счисления не может являться отрицательное число, искомое основание равно 8. |
|
Найти:
|
Ответ: 8. |
40. В системе счисления с некоторым основанием х десятичное число 144 записывается в виде 264. Укажите это основание.
|
Дано:
|
Решение Представим оба числа в развернутой форме: 1 • 10 2 +4 • 10 1 + 4 • 10 0 —
2х2 + 6х- 140 = 0. Решим
полученное уравнение: Поскольку основанием системы счисления не может являться отрицательное число, искомое основание равно 7. |
|
Найти:
|
Ответ: 7. |
41.
|
Дано: 3210 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность: 32-4=28. Найдем все делители числа 28. Это числа 2, 4, 7, 14 и 28. Основанием системы счисления не может являться число, меньшее 5, поскольку в искомой системе счисления присутствует цифра 4. Тогда все основания систем счисления, в которых запись числа 32 оканчивается на 4, — 7, 14 и 28. |
|
Найти:
|
Ответ: 7, 14, 28. |
42. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
|
Дано: 2310 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность:
Найдем все делители
числа 21. Это числа З, 7 и 21. Тогда все основания систем счисления, в
которых запись числа 23 оканчивается на 2 |
|
Найти:
|
Ответ: З, 7, 21. |
43.
|
Дано:
|
Решение Переведем в пятеричную систему счисления числа — границы заданного диапазона: 1010 = 205', 325. Запишем в пятеричной системе все числа диапазона (прибавлениями 1): 205, 215, 225, 235, 245, 305, 315, 325. Во всех записанных числах цифра 2 встречается 7 раз. |
|
Найти: Кол-во цифр 2 —9 |
Ответ: 7. |
44. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17 оканчивается на 2.
|
Дано: 1710 |
Решение Последняя цифра в записи числа представляет собой остаток от деления этого числа на основание системы счисления. Определим разность:
Найдем все делители числа 15. Это числа З, 5 и 15. Тогда все основания систем счисления, в которых запись числа 15 оканчивается на 2, З, 5 и 15. |
|
Найти:
|
Ответ: З, 5, 15. |
![]()
45. В системе счисления с некоторым основанием число 17 записывается в виде 101. Укажите это основание.
|
Дано: 101х |
Решение Представим оба числа в развернутой форме: 1 10 1 + 7 • 10 0 = 1 • х 2 +0 • х 1 + 1 • хо Х2 = 16, Решим полученное уравнение:
Поскольку основанием системы счисления не может являться отрицательное число, искомое основание равно 4. |
|
Найти:
|
Ответ: 4. |
Арифметические операции
1. Чему равна сумма чисел а = 438 и Ь = ![]()
1) 1218 3) 6916
8 4) 10000012
|
Дано: а = 438 ь = 5616 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 48 = 1002, 38 = 0112 = 438 = 1000112; 516=0101 2, 6 16 —- • Ь = 5616 = 10101102. Таким образом,
Поскольку данное число не совпадает с четвертым вариантом ответа, переведем его в восьмеричную систему счисления:
Ответ: 1718. |
|
Найти:
|
Номер ответа: 2. |
![]()
2. Вычислите сумму чисел Х и У, если Х —- 1101112, У = 1358.
Результат представьте в двоичном виде. 1) 110101002
2) 101001002
3) 100100112
4) 100101002
|
Дано: х = 1101112 У = 1358 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 18 У = 1358 = 0010111012 = 10111012. Тогда: Х + У = 1101112 + 10111012 = 100101002. ответ: 100101002. |
|
Найти:
|
Номер ответа: 4. |
З. Вычислите сумму чисел х и у при х = Аб] 6, у 758. Результат представьте в двоичной системе счисления.
1) 110110112
![]()
3) 111000112
4) 100100112
|
Дано:
758 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: А16= 10102, 616=
Таким образом:
ответ: 111000112. |
|
Найти:
|
Номер ответа: З. |
счИсмНи„я
![]()
4. Значение выражения 1016 + 108 • 102 в двоичной системе счис-
ления равно: 1) 10102
2) 110102 3) 1000002
4) 1100002
|
Дано: х- 1016 у- 108 0=10 2 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 1016 = 000100002 = 100002; 108 = 0010002 = 10002. Тогда: х + у • а = 1016 10 • 102 = 100002 + 10002 • 102 — = 100002 + 100002 = 1000002. Ответ: 1000002. |
|
Найти:
|
Номер ответа: З. |
5. Вычислите сумму двоичных чисел х и у, если х —- 10101012 и у = 10100112.
1) 101000102
2) 101010002
3) 101001002
4) 101110002
|
Дано: х = 10101012 у = 10100112 |
Решение х + у = 10101012 + 10100112 = 101010002. Ответ: 101010002. |
|
Найти:
|
Номер ответа: 2. |
6. Вычислите значение суммы 102 + 108 +1016 в двоичной системе
счисления.
1) 101000102
![]()
3) 110102
4) 101002
![]()
|
Дано: х- 102 у, 108 0=1016 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 108 = Тогда: х + у + а = 102+ 108 +1016= 102 + 10002+ 100002 = 110102. Ответ: 110102. |
|
Найти:
|
Номер ответа: З. |
![]()
Результат представьте в шестнадцатеричной системе счисления.
1) 15116
2) 1AD16
3) 41216
![]()
|
Дано: х = 2718
|
Решение Используем правила перевода целых чисел между системами счисления с основанием 8 и с основанием 2: 28 = 0102 = 102, 78 = 1112, 18=0012 х = 2718 = 101110012. Тогда:
Переведем полученное число в шестнадцатеричную систему счисления: 1101011012 = 1AD16. Ответ: 1AD16. |
|
Найти:
|
Номер ответа: 2. |
8. Вычислите сумму чисел х и у при х = А 116, у = 11012. Результат представьте в десятичной системе счисления.
1) 204 3) 183
2) 152 4) 174
|
Дано: х = А116 у = 11012 |
Решение Используем правила перевода целых чисел между системами счисления с основанием 16 и с основанием 2: А16= 10102, 116 = 0012 эх- А116= 101000012. Тогда: х + у = 101000012 + 11012= 101011102. Переведем полученное число в десятичную систему счисления: 101011102=1 2 7 +0 • 2 6 + 1 2 5 +0-24 + 1 2 3 + + 1 • 2 2 • 2 1 + 0' 2 0 = 17410. Ответ: 17410. |
|
Найти:
|
Номер ответа: 4. |
9. Вычислите сумму чисел х и у при х = 568, у - —11010012. Результат представьте в двоичной системе счисления.
![]()
2) 100101112
3) 10001112
4)
|
Дано: х = 568 11010012 |
Решение Используем правила перевода целых чисел между системами счисления с основанием 8 и с основанием 2.
х + у = 1011102 + 11010012 = 100101112. Ответ: 100101112. |
|
Найти:
|
Номер ответа: 2. |
10. Вычислите сумму чисел х и у при х = 5А16, у = 10101112.
Результат представьте в восьмеричной системе счисления.
1) 1518 3) 4338
2) 2618 4) 7028
|
Дано: х = 5А16 у = 10101112 |
Решение Используем правила перевода целых чисел между системами счисления с основанием 16 и с основанием 2: 516 - 01012 = 1012, А16= 10102 эх = 5А16= 10110102. Тогда: х + у = 10110102 + 10101112 = 101100012. Переведем полученное число в восьмеричную систему счисления: 101100012 = 2618. Ответ: 2618. |
|
Найти:
|
Номер ответа: 2. |
2) 238
3) 183
4) 313
|
Дано: х = 1278 100101112 |
Решение Используем правила перевода целых чисел между системами счисления с основанием 8 и с основанием 2:
х + у = 10101112 + 100101112 = 111011102. Переведем полученное число в десятичную систему счисления: 111011102= 1 2 7 + 1 • 2 6 + 1 • 2 5 +0 2 4 + 1 • 2 3 + 1 • 2 2 + 1 • 2 1 • 2 0 —- 23810. Ответ: 238. |
|
Найти:
|
Номер ответа: 2. |
12. Вычислите А8116 + 37716. Результат представьте в той же системе счисления.
1) 21В16
2) DF816
3) 09216
4) F4616
|
Дано:
16 |
Решение х + у = А8116 + 37716 = DF816. Ответ: DF816. |
|
Найти:
|
Номер ответа: 2. |
13. Чему равна разность чисел 10116 и 1101112?
1) 3128
8
3) 3216
4)
|
Дано: х = 10116 1101112 |
Решение Используем правила перевода целых чисел между системами счисления с основанием 16 и с основанием 2: 116 = 0012 - 12, 016 = 0002 Х = 10116 = 10000012. Тогда: х + у = 10000012 + 1101112 = 110010102. Переведем полученное число в восьмеричную систему счисления: 110010102 = 3128. Ответ: 3128. |
|
Найти:
|
Номер ответа: 1. |
14. Чему равна разность чисел 1248 и 5216?
2
2) 102
3) 1002
4) 1102
|
Дано: а = 1248 5216 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 18 = 0012, |
|
Найти:
|
Номер ответа: 2. |
15. Чему равна сумма чисел 278 и 3416?
1) 1138
2)
3) 5116
4) 1100112
|
Дано: а: 278 3416 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 28=0102, 316-0011 2, 4 16 —- = 34 16 —- 001101002 = 1101002. Таким образом, а + ь = 101112 + 1101002 = 10010112. Переведем полученное число в восьмеричную систему счисления:
Ответ: 1138. |
|
Найти:
|
Номер ответа: 1. |
![]()
16. Чему равна сумма чисел 438 и 5616?
16
2) А316
3) 1258
4) 10101012
|
Дано: а = 438 Ь = 5616 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 1002, 38 = Ь = 56 010101102 = 10101102. Таким образом,
Поскольку данное число не совпадает с четвертым вариантом ответа, переведем его в восьмеричную систему счисления:
Полученное восьмеричное число не совпадает с третьим вариантом ответа. Поэтому переведем
счисления:
Ответ: 7916. |
|
Найти:
|
Номер ответа: 1. |
17. Чему равно произведение чисел 138 и 516?
8
2) Е216
3) 658
4) 1000012
|
Дано: а = 138 Ь = 516 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 18 = 0012, 38 Поскольку данное число не совпадает с четвертым вариантом ответа, переведем его в восьмеричную систему счисления: 1101112=678. Ответ: 67 . |
|
Найти:
|
Номер ответа: 1. |
18.
8 2) 10010012 3) 2018
|
Дано: а = 158 Ь=516 |
Решение Используем правила перевода целых чисел между системами счисления с основаниями 16 (8) и с основанием 2: 18 = 0012, 58 =
1012 = а = 158 = 11012; 516 _- 01012 а ь = 11012 1012 = 10000012. Поскольку данное число не совпадает со вторым вариантом ответа, переведем его в восьмеричную систему счисления: 10000012 = 678. Полученное восьмеричное число не совпадает с первым и третьим вариантами ответов. Поэтому переведем число 10000012 в шестнадцатеричную систему счисления: 10000012 = 4116. Ответ: 41 |
|
Найти:
|
Номер ответа: 4. |
![]()
19. Чему равна разность чисел х = 10101002 и у = 10000102? 1) 110102 2) 101002 3)100102 4) 101012
|
Дано: х = 10101002 у = 10000102 |
Решение х - у = 10101002 - 10000102 = 100102. Ответ: 100102. |
|
Найти:
|
Номер ответа: З. |
20. Чему равна разность чисел х = 10116 и у —- 11001012?
![]() 448 2) 2348 3)3616 4)
6016
448 2) 2348 3)3616 4)
6016
|
Дано: х = 10116 у = 11001012 |
Решение Используем правила перевода целых чисел между системами счисления с основанем 16 и с основанием 2: 116 — ООО 12, 016 = 00002 х = 0001000000012 = 1000000012. Тогда: х - у = 1000000012 - 11001012 = 100111002. Переведем число 100111002 в восьмеричную систему счисления: 100111002 = 2348. Ответ: 2348. |
|
Найти:
|
Номер ответа: 2. |
![]()
|
Дано: = 11011102
|
Решение
|
|
Найти:
|
Номер ответа: З. |
Логика и алгоритмы
Высказывания, логические операции, кванторы,
Основные понятия математической логики
1. Для какого имени истинно высказывание:
![]() (Первая буква имени гласная —»
Четвертая буква имени согласная) ?
(Первая буква имени гласная —»
Четвертая буква имени согласная) ?
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Решение
Введем обозначения для простых высказываний:
Х = «Первая буква имени гласная» , У = «Четвертая буква имени согласная» . Построим таблицу истинности:
|
х |
|
|
|
|
|
|
1 |
|
|
|
1 |
1 |
|
|
1 |
|
|
1 |
|
1 |
1 |
1 |
|
На основании третьей строки таблицы можно сделать
вывод о том, что сложное высказывание истинно, если первое высказывание
истинно, а второе — ложно. Тогда для выполнения условий задачи высказывание
«Первая буква имени гласная» должно быть истинным, а высказывание «Четвертая
буква имени согласная» ![]() ложным (т. е. должно быть истинно высказывание « Четвертая буква имени
гласная » ). Этим условиям удовлетворяет только имя АНТОН.
ложным (т. е. должно быть истинно высказывание « Четвертая буква имени
гласная » ). Этим условиям удовлетворяет только имя АНТОН.
![]()
2. из указанных значений числа Х истинно высказывание:
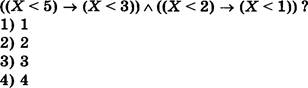
Решение
Построим таблицу истинности:
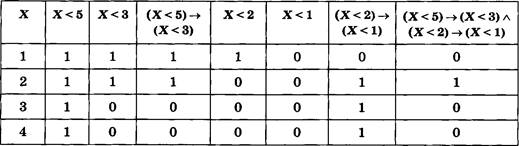
Результирующий столбец таблицы истинности содержит значение 1 (истина) для Х = 2. Номер ответа: 2.
З. Для какого числа Х истинно высказывание:
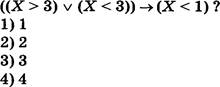
Решение
Построим таблицу истинности:
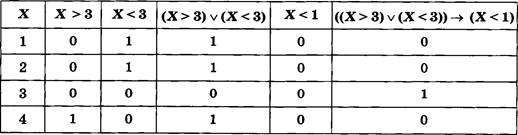
З.
![]()
4. числа Х истинно высказывание:
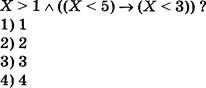
Решение
Построим таблицу истинности:
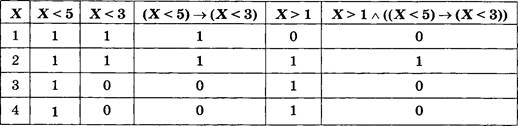
Результирующий столбец таблицы истинности содержит значение 1 (истина) для Х = 2. Номер ответа: 2.
5. Для какого из указанных значений Х истинно высказывание:
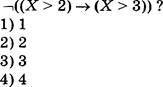
Решение
Построим таблицу истинности.

З.
![]()
6. символьного выражения неверно высказывание:
Первая буква гласная -» -, (Третья буква согласная) ?
1) abedc 2) becde З) babas 4) abcab
Решение
Введем обозначения для простых высказываний:
Х = «Первая буква гласная» ,
У = «Третья буква согласная».
Построим таблицу истинности:
|
х |
|
|
|
|
О |
О |
1 |
1 |
|
|
1 |
|
1 |
|
1 |
|
1 |
1 |
|
1 |
1 |
|
|
На основании четвертой строки таблицы можно сделать вывод о том, что сложное высказывание ложно, если оба высказывания истинны. Тогда для выполнения условий задачи должны быть истинными высказывание «Первая буква гласная» и высказывание «Третья буква согласная». Этим условиям удовлетворяет только символьное выражение abcab. Номер ответа: 4.
7. Для какого числа Х истинно высказывание:
![]()
Решение
Построим таблицу истинности.
|
х |
|
|
|
|
|
|
5 |
1 |
|
1 |
|
|
|
2 |
О |
о |
|
1 |
1 |
|
З |
1 |
|
1 |
|
|
|
4 |
1 |
О |
1 |
О |
|
2.
2.
92
![]()
8. из значений числа Z будет ложным высказывание:
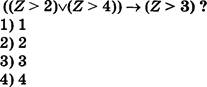
Решение
Построим таблицу истинности.
|
|
|
|
|
|
|
|
1 |
О |
о |
|
|
1 |
|
2 |
О |
о |
|
|
1 |
|
з |
1 |
|
1 |
|
|
|
4 |
1 |
|
1 |
1 |
1 |
Результирующий столбец таблицы истинности содержит значение О (ложь) для Z = З.
Номер ответа: З.
9. Для какого имени истинно высказывание:
![]() (Первая буква имени согласная -»
Третья буква имени гласная) ?
(Первая буква имени согласная -»
Третья буква имени гласная) ?
1) юлия
2) ПЕТР
3) АЛЕКСЕЙ
4) КСЕНИЯ
Решение
Введем обозначения для простых высказываний: Х = «Первая буква имени согласная» , У = «Третья буква имени гласная» .
Построим таблицу истинности:
|
х |
|
ХА У |
|
|
|
|
1 |
О |
|
|
1 |
1 |
О |
|
1 |
|
|
1 |
|
1 |
1 |
1 |
|
На основании третьей строки таблицы можно сделать вывод, что сложное высказывание истинно, если первое высказывание истинно, а второе ложно. Тогда для выполнения условий задачи высказывание «Первая буква имени согласная» должно быть истинным, а высказывание «Третья буква имени гласная» — ложным (т. е. должно быть истинно высказывание «Третья буква имени согласная Этим условиям удовлетворяет только имя ПЕТР. Номер ответа: 2.
10. Для какого из значений числа У будет истинным высказывание:
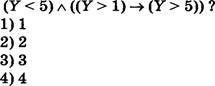
Решение
|
|
|
|
|
У<5 |
|
|
1 |
О |
о |
1 |
1 |
1 |
|
2 |
1 |
|
|
1 |
|
|
з |
1 |
|
|
1 |
|
|
4 |
1 |
|
|
1 |
|
Результирующий столбец таблицы истинности содержит значение 1 (истина) для У = 1. Номер ответа: 1.
11. Для какого символьного выражения верно высказывание:
![]() (Первая буква согласная) л (Вторая буква гласная) ?
(Первая буква согласная) л (Вторая буква гласная) ?
1) abcde 2) bcade З) babas
4) cabab
Решение
Введем обозначения для простых высказываний: Х = «Первая буква согласная» , У = «Вторая буква гласная».
Построим таблицу истинности.
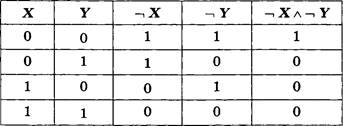
На основании первой строки таблицы можно сделать вывод, что сложное высказывание истинно, если оба высказывания ложны. Тогда для выполнения условий задачи и высказывание « Первая буква согласная», и высказывание «Вторая буква гласная» должны быть ложными. Этим условиям удовлетворяет только символьное выражение abcde.
Номер ответа: 1.
12. Для какого имени истинно высказывание:
1) ИРИНА
2) МАКСИМ
3) МАРИЯ
4) СТЕПАН
Решение
Введем обозначения для простых высказываний:
Х = «Вторая буква гласная» ,
У = «Первая буква гласная» , Z = «Последняя буква согласная» . Построим таблицу истинности:
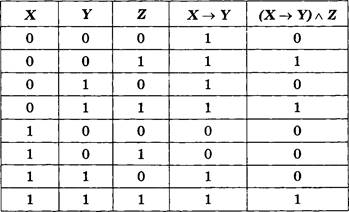
На основании результирующего столбца таблицы истинности можно сделать вывод, что сложное высказывание истинно, если два первых высказывания ложны, а третье истинно, если первое высказывание ложно, а остальные истинны, либо если все высказывания истинны. Тогда для выполнения условий задачи высказывания «Вторая буква гласная» и «Первая буква гласная» должны быть ложными, а высказывание «Последняя буква согласная» должно быть истинно. Этим условиям удовлетворяет только имя СТЕПАН (оставшимся вариантам не удовлетворяет никакое из предложенных имен).
Номер ответа: 4.
13. Для какого имени истинно высказывание:
![]() (Первая буква согласная —» Последняя
буква гласная) л л Вторая буква согласная ?
(Первая буква согласная —» Последняя
буква гласная) л л Вторая буква согласная ?
1) ИРИНА
2) СТЕПАН
3) МАРИНА
4) ИВАН
Решение
Введем обозначения для простых высказываний:
Построим таблицу истинности:
|
|
|
|
|
|
|
|
О |
О |
О |
1 |
|
|
|
о |
О |
1 |
1 |
|
|
|
О |
1 |
|
1 |
|
|
|
О |
1 |
1 |
1 |
|
|
|
1 |
О |
о |
о |
1 |
|
|
1 |
о |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
|
|
|
1 |
1 |
1 |
1 |
|
|
На основании результирующего столбца таблицы истинности можно сделать вывод, что сложное высказывание истинно, если первое и последнее высказывания истинны, а второе ложно. Тогда для выполнения условий задачи высказывания «Первая буква соглас-
ная» и «Вторая буква согласная» должны быть истинными, а высказывание «Последняя буква гласная» должно быть ложно. Этим условиям удовлетворяет только имя СТЕПАН. Номер ответа: 2.
14. Для какого имени истинно высказывание:
(Первая буква согласная -» Вторая буква согласная) л л Последняя буква гласная ?
1)КСЕНИЯ
2)МАКСИМ
3)МАРИЯ 4) СТЕПАН
Решение
Введем обозначения для простых высказываний:
|
х |
|
|
|
|
|
О |
О |
О |
1 |
|
|
О |
О |
1 |
1 |
1 |
|
|
1 |
|
1 |
|
|
|
1 |
1 |
1 |
1 |
|
1 |
О |
О |
|
|
|
1 |
О |
1 |
|
|
|
1 |
1 |
|
1 |
|
|
1 |
1 |
1 |
1 |
1 |
На основании результирующего столбца таблицы истинности можно сделать вывод, что сложное высказывание истинно, если два первых высказывания ложны, а третье истинно, если первое высказывание ложно, а остальные истинны, либо если все высказывания истинны. Тогда для выполнения условий задачи все три высказывания — «Первая буква согласная», «Вторая буква согласная» и «Последняя буква гласная» — должны быть истинными. Этим условиям удовлетворяет только имя КСЕНИЯ (оставшимся вариантам не удовлетворяет никакое из предложенных имен).
Номер ответа: 1.
15. Для какого имени истинно высказывание:
-, (Вторая буква гласная —» Первая буква гласная) л л Последняя буква согласная ?
1)ИРИНА
2)МАКСИМ
3)МАРИЯ 4) СТЕПАН
Решение
Введем обозначения для простых высказываний:
Х = «Вторая буква гласная» ,
У = «Первая буква гласная» ,
|
|
|
|
|
|
|
|
О |
О |
о |
1 |
|
|
|
О |
о |
1 |
1 |
|
|
|
О |
1 |
|
1 |
|
|
|
О |
1 |
1 |
1 |
|
О |
|
1 |
О |
О |
о |
1 |
|
|
1 |
О |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
|
|
|
1 |
1 |
1 |
1 |
|
|
На основании результирующего столбца таблицы истинности можно сделать вывод, что сложное высказывание истинно, если первое и последнее высказывания истинны, а второе ложно. Тогда для выполнения условий задачи высказывания «Вторая буква гласная» и «Последняя буква согласная» должны быть истинными, а высказывание «Первая буква гласная» должно быть ложным. Этим условиям удовлетворяет только имя МАКСИМ. Номер ответа: 2.
16. Для какого имени истинно высказывание:
![]() (Первая буква согласная -» Последняя
буква согласная) л л Вторая буква согласная ?
(Первая буква согласная -» Последняя
буква согласная) л л Вторая буква согласная ?
1) ИРИНА
2) СТЕПАН
3) МАРИЯ
4) КСЕНИЯ
4 ДергачеваЛ. М.
Решение
Введем обозначения для простых высказываний:
Х = «Первая буква согласная» , У = «Последняя буква согласная» , Z = «Вторая буква согласная» .
|
|
|
|
|
|
|
|
О |
О |
О |
1 |
|
|
|
О |
О |
1 |
1 |
|
|
|
о |
1 |
О |
1 |
|
|
|
О |
1 |
1 |
1 |
|
|
|
1 |
О |
о |
О |
1 |
|
|
1 |
О |
1 |
|
1 |
1 |
|
1 |
1 |
О |
1 |
|
|
|
1 |
1 |
1 |
1 |
|
|
На основании результирующего столбца таблицы истинности можно сделать вывод, что сложное высказывание истинно, если первое и последнее высказывания истинны, а второе ложно. Тогда для выполнения условий задачи высказывания «Первая буква согласная» и «Вторая буква согласная» должны быть истинными, а высказывание «Последняя буква согласная» должно быть ложным. Этим условиям удовлетворяет только имя КСЕНИЯ. Номер ответа: 4.
17. Для какого имени истинно высказывание:
![]() (Первая буква гласная —» Вторая
буква гласная) л л Последняя буква гласная ?
(Первая буква гласная —» Вторая
буква гласная) л л Последняя буква гласная ?
1) ИРИНА 2) МАКСИМ
3) АРТЕМ 4) МАРИЯ
Решение
Введем обозначения для простых высказываний:
Х = «Первая буква гласная» ,
У = «Вторая буква гласная» ,
Z = «Последняя буква гласная» .
Построим таблицу истинности:
|
х |
|
|
|
|
|
|
|
О |
О |
1 |
|
|
|
|
О |
1 |
1 |
О |
|
|
|
1 |
|
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
1 |
О |
О |
|
1 |
|
|
1 |
|
1 |
|
1 |
1 |
|
1 |
1 |
О |
1 |
|
|
|
1 |
1 |
1 |
1 |
|
|
18. Для какого названия животного
ложно высказывание: Заканчивается на согласную л В слове 7 букв ![]()
![]() „(Третья буква согласная) ?
„(Третья буква согласная) ?
1) Верблюд
2) Страус
З) Кенгуру 4) Леопард
Решение
Введем обозначения для простых высказываний:
Х = «Заканчивается на согласную» , У = «В слове 7 букв» ,
Z = «Третья буква согласная» .
Построим таблицу истинности:
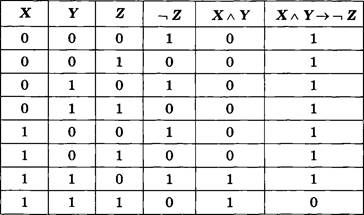
На основании результирующего столбца таблицы истинности можно сделать вывод, что сложное высказывание ложно, если все высказывания истинны. Этим условиям удовлетворяет только название животного Верблюд. Номер ответа: 1.
1) Собака
2) Жираф
З) Верблюд
4) Страус
Решение
Введем обозначения для простых высказываний: Х = «Четвертая буква гласная» , У = «Вторая буква согласная» .
Построим таблицу истинности.
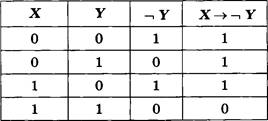
На основании третьей строки таблицы можно сделать вывод, что сложное высказывание ложно, если оба высказывания истинны. Тогда для выполнения условий задачи высказывания «Четвертая
буква гласная» и «Вторая буква согласная» должны быть истинны. Этим условиям удовлетворяет только название животного Страус. Номер ответа: 4.
20. Для какого слова ложно высказывание:
Первая буква слова согласная (Вторая буква имени гласная л л Последняя буква слова согласная) ?
1) ЖАРА
2) ОРДА
3) ОГОРОД
4) ПАРАД
Решение
Введем обозначения для простых высказываний:
Х = «Первая буква слова согласная» ,
|
|
|
|
YAZ |
|
|
О |
О |
О |
|
1 |
|
о |
о |
1 |
|
1 |
|
О |
1 |
О |
|
1 |
|
О |
1 |
1 |
1 |
1 |
|
1 |
О |
о |
|
О |
|
1 |
о |
1 |
|
|
|
1 |
1 |
|
О |
|
|
1 |
1 |
1 |
1 |
1 |
На основании таблицы можно сделать вывод, что сложное высказывание ложно, если два первых высказывания истинны, а третье ложно, если первое и последнее высказывания истинны, а второе ложно, либо если первое высказывание истинно, а остальные ложны. Тогда для выполнения условий задачи высказывания «Первая буква согласная» и «Вторая буква гласная» должны быть истинными, а высказывание «Последняя буква согласная » должно быть ложным. Этим условиям удовлетворяет только слово ЖАРА (оставшимся вариантам не удовлетворяет никакое из предложенных слов).
Номер ответа: 1.
21. Для какого числа Х истинно высказывание: (Х • (Х- 16) > -64) > 8) ?
![]()
Решение
Построим таблицу истинности:
|
|
|
|
(Х • (Х- 16) > -64) |
(Х > 8) |
|
5 |
1 |
|
|
|
|
6 |
1 |
|
|
|
|
7 |
1 |
|
|
|
|
8 |
|
|
1 |
|
22. Для какого числа Х истинно высказывание: (Х • (Х - 8) > (-25 + 2 • х» 7) ?
![]()
Решение
Построим таблицу истинности:
|
|
|
|
|
7) |
|
4 |
1 |
|
|
|
|
5 |
|
|
1 |
|
|
6 |
1 |
|
|
|
|
7 |
1 |
|
|
|
Результирующий столбец таблицы истинности содержит значение 1 (истина) для Х = 5. 2.
23. Для какого имени ложно высказывание:
(Первая буква гласная л Последняя буква согласная) -» ![]() „(Третья буква согласная) ?
„(Третья буква согласная) ?
1) ДМИТРИЙ
2) АНТОН
3) ЕКАТЕРИНА
4) АНАТОЛИЙ
Решение
Введем обозначения для простых высказываний:
Х = «Первая буква гласная» , У = «Последняя буква согласная» , Z = «Третья буква согласная».
|
|
|
|
|
|
|
|
о |
О |
О |
1 |
|
1 |
|
о |
о |
1 |
|
|
1 |
|
О |
1 |
О |
1 |
|
1 |
|
О |
1 |
1 |
|
|
1 |
|
1 |
о |
О |
1 |
|
1 |
|
1 |
О |
1 |
|
|
1 |
|
1 |
1 |
о |
1 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
О |
На основании третьей строки таблицы можно сделать вывод, что
сложное высказывание истинно, если все высказывания истинны. Тогда для
выполнения условий задачи все три высказывания ![]() «Первая буква
гласная», «Последняя буква согласная» и «Третья буква согласная» — должны быть
истинными. Этим условиям удовлетворяет только имя АНТОН. Номер ответа: 2.
«Первая буква
гласная», «Последняя буква согласная» и «Третья буква согласная» — должны быть
истинными. Этим условиям удовлетворяет только имя АНТОН. Номер ответа: 2.
24. Для какого числа Х истинно высказывание:
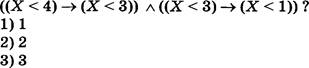
Решение
Построим таблицу истинности:
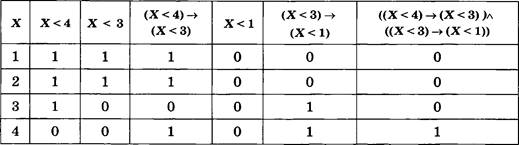
Результирующий столбец таблицы истинности содержит значение 1 (истина) для Х = 4.
Номер ответа: 4.
Задачи на построение таблиц истинности логических выражений
1.
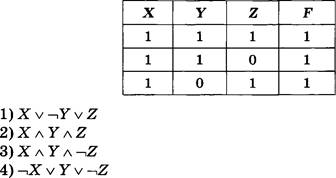
Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
Х |
У |
Z |
|
Xv-,YvZ |
XAYAZ |
Х л Ул -И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.
2. 1' одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Р. Какое выражение соответствует Е?
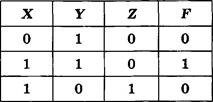

Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
Х |
У |
Z |
|
-XvYv-,Z |
Х л Ул -И |
--XA-,YAZ |
Xv-YvZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 2.
З. Символом 1' обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Е. Какое выражение соответствует Р?
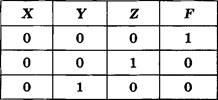
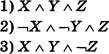
Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
|
|
|
|
|
-,XA-YAZ |
Х л Ул -И |
|
|
О |
о |
о |
1 |
|
|
|
1 |
|
О |
о |
1 |
|
|
1 |
|
|
|
о |
1 |
О |
О |
|
|
|
|
Номер ответа: 4.
|
х |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
1 |
![]()
![]()
4)XvYvZ
Решение
Воспользуемся методом нахождения логической функции по таблице истинности, используя способ, который позволит выбрать меньшее количество наборов переменных.
В таблице истинности выберем наборы переменных, при которых значение логической функции равно О. Для каждого такого набора запишем дизъюнкции всех входных переменных: при этом переменная берется без отрицания, если она имеет значение О, и с отрицанием, если она имеет значение 1. Все полученные дизъюнкции объединим знаками конъюнкции. Получим:
![]()
З.
5. 1' логическая функция от двух аргументов (А и В), заданная таблицей истинности. Какое выражение соответствует Е?
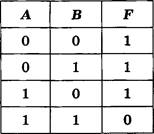
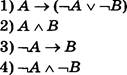
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
А |
В |
|
А |
(„А м „В) |
Ал В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 1.
6. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Е. Какое выражение соответствует Е?
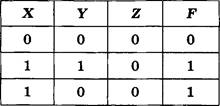

Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
Х |
У |
Z |
|
XAYAZ |
„х л Ул -И |
х л (У ма |
(Хм У) л -И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 4.
7. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Р. Какое выражение соответствует Е?
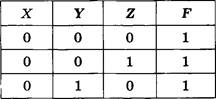
З) Х л УМ
![]()
Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
Х |
У |
Z |
|
XvYAZ |
XvYvZ |
XAYvZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.
8.
Е. Р?
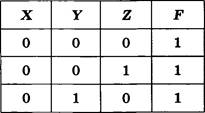
![]()
Решение
|
Х |
У |
Z |
|
|
|
|
(XvY)AZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: З.
9. Символом обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Е. Какое выражение соответствует Е?
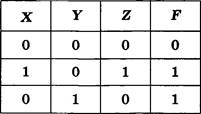
![]() 1)XAYAZ
1)XAYAZ ![]()
логических фрагментом таблицы
|
|
|
|
|
|
„хм УМ -И |
XAYvZ |
Хм У л -И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 4.
10.
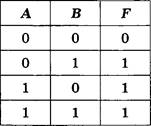
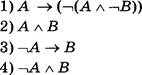
Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
А |
В |
F |
А |
( „(А л В» |
Ал В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З.
11,
Р. Е?
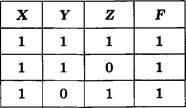
![]()
3)XvYvZ
![]()
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
Х |
У |
Z |
|
XAYAZ |
-,Xv-YvZ |
XvYvZ |
Х л У л -И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: З.
12. Символом 1' обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Р. Какое выражение соответствует Е?
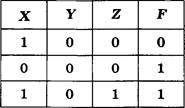
![]()
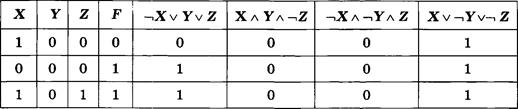
Номер ответа: 1.
13.
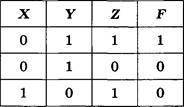

Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
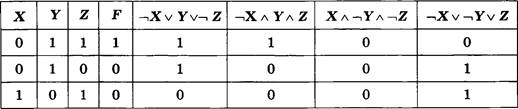
2.
Р. Р?
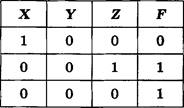

Решение
|
Х |
У |
Z |
|
„х л YAZ |
Хл-,Ул-И |
|
-,Xv YvZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 4.
15. Дан фрагмент таблицы истинности выражения Е. Какое выражение соответствует Е?
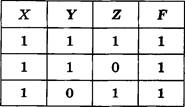
![]()
3)XvYvZ
![]()
|
Х |
У |
Z |
|
хл |
-,Xv-YvZ |
Xv YvZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: З.
16. Дан фрагмент таблицы истинности выражения Е. Какое выражение соответствует Е?
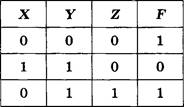
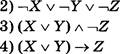
Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
Х |
У |
Z |
|
Хл YvZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.
соответствует Е?
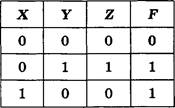
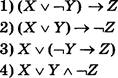
Решение
|
Х |
У |
Z |
|
(Хм „У) |
Z |
|
xvey-»a |
XvYA-Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: З.
18. Дан фрагмент таблицы истинности выражения Р. Какое выражение соответствует Е?
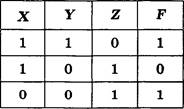
![]()
|
Х |
У |
Z |
|
XAYvZ |
|
(-Xv Y)AZ |
Х -»-,YvZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 2.
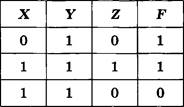
Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
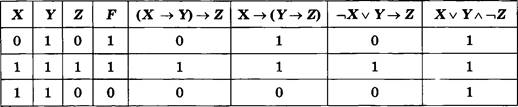
2.
фрагмент таблицы истинности соответствует Р?
|
|
|
|
|
|
О |
О |
1 |
1 |
|
1 |
о |
1 |
|
|
1 |
1 |
1 |
1 |
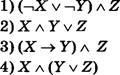
Решение
|
|
У |
z |
|
|
хл YvZ |
|
х л (уча |
|
О |
о |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
1 |
1 |
|
1 |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
Номер ответа: З.
21. Дан фрагмент таблицы истинности выражения Р. Какое выражение соответствует Р?
|
|
|
|
|
|
О |
1 |
1 |
|
|
1 |
о |
о |
1 |
|
1 |
1 |
О |
О |
![]()
3)XvYvZ
![]()
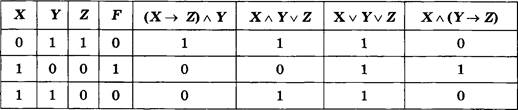
Номер ответа: 4.
22. Дан фрагмент таблицы истинности выражения Р. Какое выражение соответствует Е?
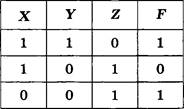
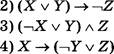
Решение
Построим фрагменты таблиц истинности для заданных наборов значений трех аргументов имеющихся логических выражений и сравним их с предложенным фрагментом таблицы истинности.
|
Х |
У |
Z |
|
XAYvZ |
|
(-xv Y)nz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.
фрагмент таблицы истинности соответствует Е?
|
|
У |
z |
|
|
О |
О |
О |
о |
|
О |
1 |
1 |
1 |
|
1 |
О |
О |
1 |
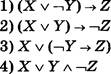
Решение
|
|
У |
z |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
о |
1 |
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
1 |
1 |
1 |
Номер ответа: З.
Преобразование логических выражений с использованием законов алгебры логики
1.
Укажите, какое
логическое выражение равносильно выражению 
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 4.
2. Какое логическое выражение равносильно выражению
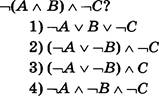
Решение
Воспользовавшись законом де Моргана, преобразуем исходное логическое выражение:
![]()
Номер ответа: 2.
З. Укажите, какое логическое выражение равносильно
выражению 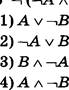 (—И л В)?
(—И л В)?
Решение
![]()
Номер ответа: 1.
4. Какое логическое выражение равносильно выражению
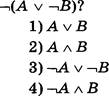
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 4.
5. Какое логическое выражение эквивалентно выражению
![]() 2) Ал
ВАС
2) Ал
ВАС ![]()
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 2.
6. Какое логическое выражение эквивалентно выражению
![]()
1) Ал ВАС
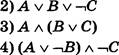
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: З.
7.
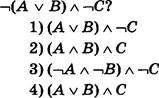
Решение
Воспользовавшись законом де Моргана, преобразуем исходное логическое выражение:
![]()
Номер ответа: З.
8. Какое логическое выражение эквивалентно выражению
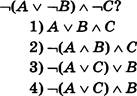
Решение
Воспользовавшись законами де Моргана, двойного отрицания и сочетательным законом, преобразуем исходное логическое выражение:
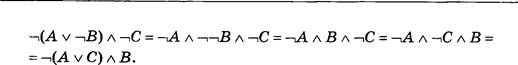
Номер ответа: 4.
9. Какое логическое выражение эквивалентно выражению
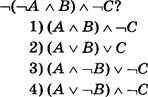
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 4.
10. Какое логическое выражение эквивалентно выражению
![]()
2)AvBvC
![]()
Решение
Заменив операцию импликации операциями дизъюнкции и инверсии и воспользовавшись законом двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 2.
11. Какое логическое выражение эквивалентно выражению
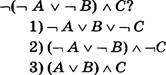
4) Ал ВАС
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 4.
12. Какое логическое выражение эквивалентно выражению
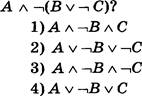
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 1.
13. Какое логическое выражение эквивалентно выражению
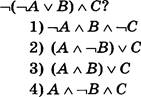
Решение
![]() v В) л С = —т—и4 л л
С = А л л С. Номер ответа: 4.
v В) л С = —т—и4 л л
С = А л л С. Номер ответа: 4.
14. Какое логическое выражение эквивалентно выражению
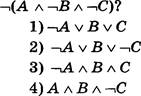
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 1.
15. Какое логическое выражение
законами де Моргана двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: З.
16. Какое логическое выражение эквивалентно выражению
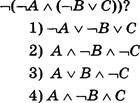
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
17. Какое логическое выражение эквивалентно выражению
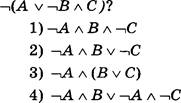
Решение
Воспользовавшись законами де Моргана и двойного отрицания, а также распределительным законом, преобразуем исходное логическое выражение:
![]()
Номер ответа: 4.
18. Какое логическое выражение
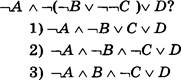
законами де Моргана двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: З.
19. Какое логическое выражение эквивалентно выражению
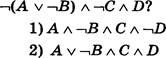
3) -AvBv-CvD
![]()
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
20. Какое логическое выражение эквивалентно выражению

Решение
Воспользовавшись законами де Моргана и двойного отрицания, а также переместительным законом, преобразуем исходное логическое выражение:
![]() В л —С)л = В л = (В
С) л „А = —и4 л (В С). Номер ответа: 4.
В л —С)л = В л = (В
С) л „А = —и4 л (В С). Номер ответа: 4.
21. Какое логическое выражение А л ев С)?
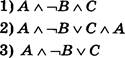
распределительным переместительным законами, преобразуем исходное логическое выражение:
![]()
Номер ответа: 2.
22. Какое логическое выражение эквивалентно выражению
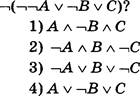
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: 2.
23.
З) Ал В л -С
![]()
Решение
Воспользовавшись законами де Моргана и двойного отрицания, преобразуем исходное логическое выражение:
![]()
Номер ответа: З.
Преобразование логических выражений
1. Сколько различных решений имеет уравнение:
![]()
где Ј, К, L, М, N — логические переменные? (В ответе не нужно перечислять все различные наборы значений Ј, К, L, М и N, при которых выполнено данное равенство. Достаточно указать только количество таких наборов.)
Решение
Высказывание еЈ л —К л 1., л —М л (N -,N) ложно, если ложно хотя бы одно из высказываний: Ј, —К, L, „М, (N v -,N). Таким образом, или Ј = О, или —К = О, или 1., = О, или —М = О, или Nv—N = О. Однако Nv—N = 1 при любом значении (закон исключения третьего).
Следовательно, необходимо найти количество наборов для оставшихся значений четырех логических переменных, а затем умножить полученный результат на 2 (поскольку уравнение будет иметь решения и при лт = О, и лт = 1).
Общее количество наборов значений логических переменных Ј, „К, L мы найдем, воспользовавшись формулой 2 l = N, где i — количество логических переменных, а N — возможное число наборов для данных переменных: 2 4 = 16.
Все найденные наборы значений приведут к необходимому результату, кроме набора 1, 1, 1, 1 (так как в этом случае еЈ л —К л 1., л л „М = 1). Следовательно, общее количество наборов значений логических переменных Ј, „К, 1., „М: 16 — 1 = 15.
Найдем количество различных решений уравнения е.Г л ![]() л
1., л л л (N х./ —N) = О, умножив 15 на 2: получим 30 наборов.
л
1., л л л (N х./ —N) = О, умножив 15 на 2: получим 30 наборов.
Ответ: 30.
2. Каково наибольшее целое число Х,
при котором истинно высказывание: (90 ![]() (Х < (Х- 1)) ?
(Х < (Х- 1)) ?
Решение
Ответ: 9.
З. Сколько различных решений имеет уравнение:
![]()
где К, L, М, лт — логические переменные? (В ответе не нужно перечислять все различные наборы значений К, L, М и N, при которых выполнено данное равенство. Достаточно указать только количество таких наборов.)
Решение
Высказывание (К л L л М) v (—L л —М л N) истинно, если истинно хотя бы одно из высказываний: (К л л М) или (—L л —М л N). Таким образом, или К = 1 и = 1 и М = 1, при этом = О или лт = 1; или 1., = О и М = О, N = 1, при этом К = 1 или К = О. Следовательно, уравнение имеет четыре решения.
Ответ: 4.
4. Укажите значения переменных К, L, М, N, при которых ложно логическое выражение:
![]()
Ответ запишите в виде строки из четырех символов — значений переменных К, L, М и (в указанном порядке). Например, строка 1101 соответствует К = 1, 1., = 1, М = О, = 1.
Решение
Высказывание (—К х../ М) -» (-,L М ж./ N) ложно, если высказывание (—К v М) истинно, а высказывание (—L v М v N) ложно. Таким образом, 1., = 1 и М = О и лг = О, тогда К = О. Следовательно, значения переменных, при которых логическое выражение ложно: 0100. Ответ: 0100.
5. Каково наименьшее целое положительное число Х, при котором будет ложным высказывание:
(4 > -(4 + Х) • Х) -» (30 Х) ?
Решение
Высказывание (4 > —(4 + Х) • Х) -» (30 > Х • Х) будет ложным, только если высказывание 4 > —(4 + Х) • Х будет истинным, а высказывание 30 > Х • Х — ложным.
Следовательно, наименьшее целое положительное число Х, при котором истинно высказывание (4 > —(4 + Х) • Х) -» (30 > Х • Х), равно 6.
Ответ: 6.
6. Каково наибольшее целое положительное число Х, при котором истинно высказывание:
«х - 1) < Х) (40 Х)?
Решение
Данная импликация содержит в левой части высказывание (Х — 1) Х, которое будет истинным при любом значении Х. Тогда высказывание ((Х — 1) Х) (40 > Х • Х) истинно, только если истинно высказывание 40 > Х • Х, стоящее в его правой части. В этом случае наибольшее целое положительное число Х равно 6. Следовательно, наибольшее целое число Х, при котором истинно высказывание ((Х — 1) < Х) —» (40 > Х • Х), также равно 6. Ответ: 6.
7. Укажите значения переменных К, L, М, N, при которых ложно логическое выражение:
НМ L) л К) -» л „М) ЛУ).
Ответ запишите в виде строки из четырех символов — значений переменных К, L, М и N (в указанном порядке). Например, строка 1101 соответствует К = 1, L = 1, М = О, лт = 1.
Решение
Высказывание v L) л К) —» л „М) •,./ N) ложно, если высказывание „(М L) л К истинно, а высказывание (—К л -,М) v лт ложно. Таким образом, К = 1 и М = О и L = О, тогда лт = О. Следовательно, значения переменных, при которых логическое выражение ложно: 1000. ответ: 1000.
8. Каково наименьшее натуральное число Х, при котором будет ложным высказывание:
![]()
Решение
9. Укажите значения логических переменных Р, Q, S, Т, при которых ложно логическое выражение:
![]()
Ответ запишите в виде строки из четырех символов — значений переменных Р, Q, S, Т (в указанном порядке).
Решение
Высказывание (Р —0) v (Q —» (S Т)) ложно, если ложны высказыванияР v EIQ (S Т). Таким образом, Р = О и 1, T0№aS = О и Т = О. Следовательно, значения переменных, при которых логическое выражение ложно: 0100. Ответ: 0100.
10. Каково наибольшее целое положительное число Х, при котором будет ложным высказывание: ((Х + 6) Х + 9 > О)» (Х • Х > 20)? 5 ДергачеваЛ. М.
Решение
Высказывание ((Х + 6) • Х + 9 > О) (Х • Х > 20) будет ложным, только если высказывание (Х + 6) • Х + 9 > О будет истинным, а высказывание Х • Х 20 — ложным.
Высказывание (Х + 6) • Х + 9 О истинно при Х е (—оо;—З);(—З; +00). При этом высказывание Х • Х > 20 должно быть ложным, тогда наибольшее целое положительное значение Х равно 4.
Следовательно, наибольшее целое положительное число Х, при котором ложно высказывание ((Х + 6) •Х + 9 > О) -» (Х • Х > 20), равно 4.
Ответ: 4.
11. Укажите значения переменных К, L, М, N, при которых ложно логическое выражение:
![]()
Ответ запишите в виде строки из четырех символов — значений переменных К, L, М и лт (в указанном порядке). Например, строка 1101 соответствует К = 1, L = 1, М = О, = 1.
Решение
12. Укажите значения переменных К, L, М, N, при которых истинно логическое выражение:
![]()
Ответ запишите в виде строки из четырех символов — значений переменных К, L, М и лт (в указанном порядке). Например, строка 1101 соответствует К = 1, 1., = 1, М = О, лк = 1.
Решение
ВЫСКа3ЫВаНИе (К М) л (К л (М л -4.“ л N)) истинно, если истинны высказывания К М, К -» —М и —К (М л —L л л N). Таким образом: К = О, М = 1, тогда L = О, дт = 1. Следовательно, значения переменных, при которых логическое выражение истинно: 0011. Ответ: 0011.
13. А, В и С — целые числа, для которых истинно высказывание:
![]()
Чему равно С, если А = 45 и В = 18?
Решение
Подставим значения А и В в заданное высказывание и упростим его:
(С С<В) л + 1 л „(С + 1 < В) = (С < 45 18) л л „(С + 1 < 1 45) л (С + 1 18), = (С < 45) л (С 44) л (С 17) = (С < 45) (С 44).
Тогда значение С, при котором логическое высказывание (С < А vC < В) л + 1 <А) л „(С + 1 В) истинно, равно 44. Ответ: 44.
![]() 14. Сколько различных решений
имеет уравнение:
14. Сколько различных решений
имеет уравнение:
![]()
где К, L, М, лт — логические переменные? (В ответе не нужно перечислять все различные наборы значений К, L, М и N, при которых выполнено данное равенство. Достаточно указать только количество таких наборов.)
Решение
Следовательно, общее количество наборов значений логических переменных равно 4 + З = 7. Ответ: 7.
15. Сколько различных решений имеет уравнение:
![]()
где К, L, М, N — логические переменные? (В ответе не нужно перечислять все различные наборы значений К, L, М и N, при которых выполнено данное равенство. Достаточно указать только количество таких наборов.)
Решение
Высказывание (К v L v М) л (—L л —М л N) истинно, только если истинны оба высказывания: (К v 1., v М) и (—L л —М л N). Таким образом, 1., = О, М = О, = 1, тогда К = 1.
Следовательно, данное уравнение имеет только одно решение. Ответ: 1.
16. Сколько различных решений имеет уравнение:
(К ![]() ем л N) = 1,
ем л N) = 1,
где К, L, М, лт — логические переменные? (В ответе не нужно перечислять все различные наборы значений К, L, М и N, при которых выполнено данное равенство. Достаточно указать только количество таких наборов.)
Решение
Общее количество наборов значений логических переменных К, L, М, лт мы найдем, воспользовавшись формулой: = N, где i — количество логических переменных, N — возможное число наборов для данных переменных: 2 4 = 16.
Определим, в каком случае высказывание (К л 1., л М) -» (—М л N) ложно. Это возможно, только если истинно высказывание (К л L л М), а высказывание (—М л N) ложно. Тогда К = 1, L = 1, М = 1 (при этом высказывание К л 1., л М истинно), а 1 или = О. То есть высказывание (К л 1., л М) —» (—М л дт) ложно только для двух наборов переменных. Значит, данное высказывание будет истинно для 16 — 2 = 14 наборов переменных. Ответ: 14.
17.
![]()
где К, L, М, лт — логические переменные? (В ответе не нужно перечислять все различные наборы значений К, L, М и N, при которых выполнено данное равенство. Достаточно указать только количество таких наборов.)
Решение
Высказывание (К v L) л (М N) истинно, только если истинны оба высказывания: (К v L) и (М v N). При этом каждое из высказываний истинно для трех наборов переменных.
Следовательно, все заданное уравнение имеет З • З = 9 решений. Ответ: 9.
18.Сколько различных решений имеет уравнение:
![]()
где А, В, С, D — логические переменные? (В ответе не нужно перечислять все различные наборы значений А, В, С, D, при которых выполнено данное равенство. Достаточно указать количество таких наборов.)
Решение
Высказывание ( D л -,D) ложно при любом значении D ( D = 1 или D = О). Тогда высказывание (А -» В) л С должно быть истинно, а это возможно, только если истинны оба высказывания: (А > В) и С; при этом высказывание А > В истинно для трех наборов переменных.
Следовательно, заданное уравнение имеет З • 2 = 6 решений. Ответ: 6.
19. Сколько различных решений имеет уравнение: ![]() л К л л
-леЈ л (L = О, где Ј, К, L, М, лт — логические переменные? (В
ответе не нужно перечислять все различные наборы значений Ј, К, L, М и N, при
которых выполнено данное равенство. Достаточно указать только количество таких
наборов.)
л К л л
-леЈ л (L = О, где Ј, К, L, М, лт — логические переменные? (В
ответе не нужно перечислять все различные наборы значений Ј, К, L, М и N, при
которых выполнено данное равенство. Достаточно указать только количество таких
наборов.)
Решение
Высказывание —М л К л л л (L v —С) ложно, если ложно хотя бы одно из высказываний: „М, К, —,N, -4 и 1., v -,L. Таким образом, или —М = О, или К = О, или = О, или --Ј = О, или L v = О. Однако 1., = 1 при любом значении 1., (закон исключения третьего). Следовательно, необходимо найти количество наборов для оставшихся значений четырех логических переменных, а затем умножить полученный результат на 2 (поскольку уравнение будет иметь решения и при L = О, и при = 1).
Все найденные наборы значений приведут к необходимому результату, кроме набора 1, 1, 1, 1 (так как в этом случае —М л К л л л = 1). Значит, общее количество наборов значений логических переменных —,М, К, —,N, —Ј: 16 — 1 = 15.
Найдем количество различных решений уравнения —М л К л —N л л --Ј v --L) = О, умножив 15 на 2: получим 30 наборов. Ответ: 30.
20. Укажите значения переменных К, L, М, N, при которых ложно логическое выражение:
![]()
Ответ запишите в виде строки из четырех символов — значений переменных К, L, М и N (в указанном порядке). Например, строка 1101 соответствует К = 1, 1., = 1, М = О, лт = 1.
Решение
Высказывание (К —» „М) v (-,L л М л К) v ложно, если ложны все высказывания: (К -» „М), (—L л М л К) и -,N. Таким образом,
![]() = О, значит, N= 1, тогда тельно, --,L = О, тогда = 1.
= О, значит, N= 1, тогда тельно, --,L = О, тогда = 1.
Таким образом, значения переменных, при которых логическое
![]()
Цепочки (конечные последовательности),
1. Цепочка из трех бусин, помеченных латинскими буквами, формируется по следующему правилу. В конце цепочки стоит одна из бусин А, В, С. На первом месте — одна из бусин В, D, С, которой нет на третьем месте. В середине — одна из бусин А, С, Е, В, не стоящая на первом месте. Какая из перечисленных цепочек создана по этому правилу?
1) свв
2) ВАС
3) ВС!)
4) всв
Решение
По указанному правилу формируется только первая цепочка.
Вторая цепочка содержит бусину Е на первом месте, что противоречит условию задачи.
Третья цепочка содержит бусину D на последнем месте, что противоречит условию задачи.
Четвертая цепочка содержит повторяющиеся бусины на первом и на последнем местах, что противоречит условию задачи. Ответ: 1.
2. В формировании цепочки из четырех бусин используются следующие правила. В конце цепочки стоит одна из бусин Р, N, Т, О. На первом — одна из бусин Р, R, Т, О, которой нет на третьем месте. На третьем месте — одна из бусин О, Р, Т, не стоящая в цепочке последней. Какая из перечисленных цепочек могла быть создана с учетом этих правил?
1) PORT
2) ттто
3) ттоо
4) ООРО
Решение
По указанному правилу формируется только четвертая цепочка.
Первая цепочка содержит бусину R на третьем месте, что противоречит условию задачи.
Вторая бусины Т на первом и на третьем местах, что противоречит условию задачи.
Третья цепочка содержит повторяющиеся бусины на третьем и на последнем местах, что противоречит условию задачи.
Ответ: 4.
З. Для составления цепочек разрешается использовать бусины пяти типов, обозначаемых буквами А, Б, В, Е, И. Каждая цепочка должна состоять из трех бусин, при этом должны соблюдаться следующие правила:
![]() на первом месте стоит одна из бусин-букв:
А, Е, И;
на первом месте стоит одна из бусин-букв:
А, Е, И; ![]() после гласной буквы в цепочке не может
снова идти гласная, а после согласной — согласная;
после гласной буквы в цепочке не может
снова идти гласная, а после согласной — согласная; ![]() последней буквой не
может быть А.
последней буквой не
может быть А.
Какая из цепочек построена по этим правилам?
1)АИБ
2) ЕВА
3) БИВ
4) ИБИ
Решение
По указанному правилу формируется только четвертая цепочка.
Вторая цепочка содержит букву А на последнем месте, что противоречит условию задачи.
Третья цепочка содержит букву Б на третьем месте, что противоречит условию задачи.
Ответ: 4.
4. Для составления цепочек используются бусины, помеченные буквами: А, В, С, 1), Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква согласная, и любая согласная, если первая — гласная. На третьем месте — одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Какая из перечисленных цепочек создана по этому правилу?
1) СВЕ
2) ADD
3) ЕСЕ
4) EAD
Решение
По указанному правилу формируется только вторая цепочка.
Первая цепочка содержит две подряд идущие согласные буквы на первом и на втором местах, что противоречит условию задачи.
Третья цепочка содержит повторяющиеся бусины на первом и на последнем местах, что противоречит условию задачи.
Четвертая цепочка содержит две подряд идущие согласные буквы на первом и на втором местах, что противоречит условию задачи. Ответ: 2.
5. Цепочка из трех бусин формируется по следующему правилу. На первом месте в цепочке стоит одна из бусин А, Б, В. На втором — одна из бусин Б, В, Г. На третьем месте — одна из бусин А, В, Г, не стоящая в цепочке на первом или на втором месте. Какая из следующих цепочек создана по этому правилу:
1) АГБ
2) ВАГ
3) БГГ
4) ББГ
Решение
По указанному правилу формируется только четвертая цепочка.
Первая цепочка содержит букву Б на третьем месте, что противоречит условию задачи.
Третья цепочка содержит две повторяющиеся буквы Г на втором и на третьем местах, что противоречит условию задачи. Ответ: 4.
6. Для составления 4-значных чисел используются цифры 1, 2,
З, 4, 5. При этом соблюдаются следующие правила: ![]() на первом месте стоит
одна из цифр 1, 2 или З;
на первом месте стоит
одна из цифр 1, 2 или З;
• после каждой четной цифры идет нечетная, а после каждой нечетной — четная; е третьей цифрой не может быть цифра 5.
Какое из следующих чисел получено по этим правилам?
1) 4325
2) 1432
3) 1241
4) 3452
Решение
По указанному правилу формируется только вторая цепочка чисел.
Первая цепочка содержит цифру 4 на первом месте, что противоречит условию задачи.
Третья две подряд идущие четные цифры на втором и на третьем местах, что противоречит условию задачи.
Четвертая цепочка содержит цифру 5 на третьем месте, что противоречит условию задачи. Ответ: 2.
7. Для составления цепочек используются разные бусины, которые условно обозначаются цифрами 1, 2, З, 4, 5. Каждая такая цепочка состоит из 4 бусин. При этом соблюдаются следующие правила построения цепочек:
•
на первом месте стоит одна из бусин 1, 4 или 5; е после четной
цифры в цепочке не может идти снова четная, а после нечетной — нечетная; ![]() последней
цифрой не может быть цифра З.
последней
цифрой не может быть цифра З.
Какая из перечисленных цепочек создана по этим правилам?
1) 4325
2) 4123
3) 1241
4) 3452
Решение
Вторая цепочка содержит цифру З на последнем месте, что противоречит условию задачи.
Третья цепочка содержит две подряд идущие четные цифры на втором и на третьем местах, что противоречит условию задачи.
Четвертая цепочка содержит цифру З на первом месте, что противоречит условию задачи.
Ответ: 1.
8. Для составления цепочек используются разноцветные бусины: темные — синяя (С) и зеленая (З) и светлые — желтая (Ж), белая (Б) и голубая (Г). На первом месте в цепочке стоит бусина синего или желтого цвета. В середине цепочки — любая из светлых бусин, если первая бусина темная, или любая из темных бусин, если первая бусина светлая. На последнем месте — одна из бусин белого, голубого или зеленого цвета, не стоящая в цепочке в середине. Какая из перечисленных цепочек создана по этому правилу?
2) БГЗ
3) сгж
4) ЖБС
Решение
По указанному правилу формируется только первая цепочка.
Вторая цепочка содержит белую бусину на первом месте, что противоречит условию задачи.
Третья цепочка содержит желтую бусину на последнем месте, что противоречит условию задачи.
Четвертая цепочка содержит две подряд идущие светлые бусины на первом и на втором местах, что противоречит условию задачи.
Ответ: 1.
9. Цепочка из трех бусин формируется по следующему правилу: на первом месте стоит одна из бусин Б, В, Г. На втором — одна из бусин А, Б, В. На третьем месте — одна из бусин А, В, Г, не стоящая в цепочке на первом или втором месте. Какая из цепочек создана по этому правилу?
1) АГБ
2) ВАА
3) БГВ
4) ГБА
Решение
По указанному правилу формируется только четвертая цепочка.
Вторая цепочка содержит повторяющиеся бусины А на втором и на третьем местах, что противоречит условию задачи.
Третья цепочка содержит бусину Г на втором месте, что ПРОТИВ0речит условию задачи. Ответ: 4.
10. Для составления цепочек используются разноцветные бусины: темные — красная (К), синяя (С) и зеленая (З) и светлые — желтая (Ж) и белая (Б). На первом месте в цепочке стоит бусина красного, синего или белого цвета. В середине цепочки — любая из светлых бусин, если первая бусина темная, или любая из темных бусин, если первая бусина светлая. На последнем месте — одна из бусин белого, желтого или синего цвета, не стоящая в цепочке в середине. Какая из перечисленных цепочек создана по этому правилу?
1) юкс
2) БКЗ
3) сзж
4) зкс
Решение
По указанному правилу формируется только первая цепочка.
Вторая зеленую бусину на третьем месте, что противоречит условию задачи.
Третья цепочка содержит две подряд идущие темные бусины на первом и на втором местах, что противоречит условию задачи.
Четвертая цепочка содержит зеленую бусину на первом месте, что противоречит условию задачи. Ответ: 1.
11. Для составления цепочек используются разные бусины, которые условно обозначаются цифрами 1, 2, З, 4, 5. Каждая такая цепочка состоит из 4 бусин. При этом соблюдаются следующие правила построения цепочек. На втором месте стоит одна из бусин 2, З или 4. После четной цифры в цепочке не может идти снова четная, а после нечетной — нечетная. Последней цифрой не может быть цифра 2.
Какая из перечисленных цепочек создана по этим правилам?
1) 4321
2) 4123
3) 1241
4) 3452
Решение
Вторая цепочка содержит бусину с цифрой 1 на втором месте, что противоречит условию задачи.
Третья цепочка содержит две подряд идущие четные цифры на бусинах, стоящих на втором и на третьем местах, что противоречит условию задачи.
Четвертая цепочка содержит бусину с цифрой 2 на последнем месте, что противоречит условию задачи. Ответ: 1.
12. Джентльмен пригласил даму в гости, но вместо кода цифрового замка своего подъезда отправил ей такое сообщение: «В последовательности 52186 все четные цифры нужно разделить на 2, а из нечетных вычесть 1. Затем надо удалить из полученной последовательности первую и последнюю цифры» . Определите код цифрового замка.
1) 104
2) 107
3) 218
4) 401
Решение
Выполним действия с числами последовательности: 5, 2, 1, 8, 6.
После деления на 2 всех четных чисел и вычитания 1 из всех нечетных чисел данная последовательность примет вид: 4, 1, О, 4, З.
Удалив из полученной последовательности первую и последнюю цифры, получим: 1, О, 4.
Таким образом, указанному правилу соответствует первый код (104).
Номер ответа: 1.
13. Кассир забыл пароль к сейфу, но помнил алгоритм его получения из строки «АУУ1УАВС55»: если последовательно удалить из этой строки цепочки символов «УУ» и «АВС», а затем поменять местами символы А и У, то полученная последовательность и будет паролем. Определите пароль к сейфу.
1) АIУ55
2) А155
3) А55У1
4) УIА55
Решение
Выполним действия с символами последовательности «АУУ1УАВС55».
После перестановки символов А и У получим: «У1А55» .
Таким образом, указанному правилу соответствует четвертый пароль.
Номер ответа: 4.
14. Вася забыл пароль своей учетной записи в Windows ХР, но помнил алгоритм его получения из строки подсказки «B265C42GC4»: если все последовательности символов «04» заменить на «F16», а затем из получившейся строки удалить все трехзначные числа, то полученная последовательность и будет паролем.
Определите пароль учетной записи Васи.
1) BFGF16 2) BF42GF16
3) BFGF4 4) BF16GF
Решение
Выполним действия с символами последовательности «B265C42GC4».
После замены всех последовательностей символов «04» на «F16» исходная последовательность примет вид: «B265F162GF16».
После удаления из этой строки всех трехзначных чисел получим: «BFGF16».
Таким образом, указанному правилу соответствует первый пароль.
Номер ответа: 1.
15. Вася забыл пароль своей учетной записи в Windows ХР, но помнил алгоритм его получения из строки подсказки «23ABN12QR8N» : если последовательности символов «АВ» и «QR» поменять местами, а затем из получившейся строки удалить все символы «N» , то полученная последовательность и будет паролем. Определите пароль учетной записи Васи.
1) 23AB12QR8
2) 23QR12AB8
3) 23QRAB8
4) 23QR128
Решение
Выполним действия с символами последовательности «23ABN12QR8N».
После удаления из строки всех символов N мы получим последовательность: «23QR12AB8».
Таким образом, указанному правилу соответствует второй па-
Роль. ![]()
Номер ответа: 2.
16. Шифровальщику нужно восстановить забытое кодовое слово. Он помнит, что на третьем месте в нем стоит одна из букв — Д, З или Е. На четвертом месте стоит буква И, К или Е, не стоящая на третьем месте. На первом месте — одна из букв Д, З, К или И, не стоящая в слове на втором или на четвертом месте. На втором месте стоит любая согласная, если третья буква гласная, или любая гласная, если третья — согласная. Определите кодовое слово.
1) дипк
2) КДЕК
3) ИЗЕЕ
4) ДИДЕ
Решение
По указанному правилу формируется только четвертая цепочка (слово).
Первая цепочка содержит две гласные буквы на втором и на третьем местах, что противоречит условию задачи.
Вторая цепочка содержит повторяющиеся буквы К на первом и на четвертом местах, что противоречит условию задачи.
Третья цепочка содержит повторяющиеся буквы Е на третьем и на последнем местах, что противоречит условию задачи. Ответ: 4.
17. Витя приёласил своего друга Сергея в гости, но не сказал ему код от цифрового замка своего подъезда, а послал следующее SMS-c006u.xeHI•re: «В последовательности чисел З, 1, 8, 2, 6 все числа больше 5 надо разделить на 2, а затем удалить из полученной последовательности все четные числа» . Выполнив указанные в сообщении действия, Сергей получил код для цифрового замка. Какой это был код?

Решение
После деления на 2 чисел, больших пяти, эта последовательность примет вид: З, 1, 4, 2, З.
После удаления всех четных чисел из последовательности мы получим: З, 1, З.
Таким образом, по указанному правилу формируется третья цепочка (код 313).
Номер ответа: З.
18. Вася забыл пароль для запуска компьютера, но помнил алгоритм его получения из строки подсказки «kBRA69kBk»: если все последовательности символов «RA6» заменить на «FL», «КВ» на « 12В» , а затем из получившейся строки удалить три последних символа, то полученная последовательность и будет паролем. Определите пароль.
1) 12BFL91
2) 12BFL9
3) КВТ,912ВК
4) 12BFL1
Решение
Выполним действия с символами последовательности «kBRA69kBk».
После того как все последовательности символов «RA6» будут заменены на «FL», а «КВ» на «12В», исходная последовательность примет вид: «12BFL912Bk» .
После удаления из этой строки трех последних символов мы получим: « 12BFL91 ».
Таким образом, по указанному правилу формируется первая цепочка (пароль).
Номер ответа: 1.
19. Маша забыла пароль для запуска компьютера, но помнила алгоритм его получения из строки подсказки «КВМАМ9КВК» : если все последовательности символов «МАМ» заменить на «RP» , «КВК» на «1212», а затем из получившейся строки удалить три последних символа, то полученная последовательность и будет паролем. Определите пароль.
1) kBRP91
2) 1212RP91
3) kBRP9 4) кв91212
Решение
После того как все последовательности символов «МАМ» будут заменены на «RP», а «КВК» на «1212», исходная последовательность примет вид: «kBRP91212».
После удаления из этой строки трех последних символов мы получим: «kBRP91 ».
Таким образом, по указанному правилу формируется первая цепочка (пароль).
Номер ответа: 1.
20. Глаша забыла пароль для запуска компьютера, но помнила алгоритм его получения из строки подсказки «QWER3QWER1»: если все последовательности символов «QWER» заменить на «QQ» , а затем из получившейся строки удалить сочетания символов «3Q», то полученная последовательность и будет паролем. Определите пароль.
1) 3QQQ1
2) QQ1
3) QQQ
4) QQQ1
Решение
Выполним действия с символами последовательности «QWER3QWER1».
После того как все последовательности символов «QWER» будут заменены на «QQ» , последовательность примет вид: «QQ3QQ1 ».
После удаления из этой строки сочетания символов «3Q» мы получим: «QQQ1».
Таким образом, указанному правилу соответствует четвертый пароль.
Номер ответа: 4.
Выигрышные стратегии
1. Два игрока играют в следующую игру.
Имеются три кучи камней, содержащих соответственно 2, З и 4 камня. За один ход игроку разрешается или удвоить количество камней в какой-нибудь куче, или добавить по два камня в каждую из трех куч. Предполагается, что у каждого игрока имеется неограниченный запас камней.
Выигрывает игрок, после хода которого в какой-нибудь куче становится не менее 15 камней или во всех трех кучах суммарно СТЕНОвится не менее 25 камней.
Решение
Для решения задачи составим таблицу (дерево развития игры при различных продолжениях; в обозначениях числа в скобках указывают количества камней в каждой из трех куч, а число после скобок — суммарное количество камней).
Если игрок I сделает свой первый ход (2,3,4) -» (4,3,4), то игрок II при правильной игре сделает ход (4, 3,4) -» (4,6,4), что приводит к проигрышу игрока I (так как из состояния (4,6,4) игрок I может своим ходом перевести игру в одно из четырех состояний — (8,6,4), (4, 12,4), (4,6,8), (6,8,6), и для любого из этих состояний найдется ход игрока П, дающий ему выигрыш).
Если игрок I сделает свой первый ход (2, 3,4) -» (2,6,4), то игрок П при правильной игре сделает ход (2,6,4) -» (4,6,4), что приводит к выигрышу игрока П.
Если игрок I сделает свой первый ход (2,3,4) —» (2,3,8), то его проигрыш очевиден, так как игрок П, как указано в таблице, добьется выигрышного состояния игры (2,3, 16).
Наконец, если игрок I сделает свой первый ход (2,3,4) -» (4,5,6), то он выигрывает игру, так как на любой из четырех возможных ответов игрока П (см. таблицу) существует выигрывающий ход игрока 1.
|
Начальная позиция |
1-й ход первого игрока |
1-й ход второго игрока |
Анализ рассчитанных состояний игры |
|
|
(4, З, 4) 11 |
(8, з, 4) 15 |
Проигрыш игрока I при любом продолжении игры |
|
(4, 4) 14 |
|||
|
(4, з, 8) 15 |
|||
|
(6, 5, 6) 17 |
|||
|
(2, 6, 4) 12 |
(4, 4) 14 |
||
|
(2, 12, 4) 18 |
|||
|
(2, 6, 8) 16 |
|||
|
(4, 8, 6) 18 |
|||
|
(2, з, 8) 13 |
Проигрыш игрока I при ходе игрока П (2, з, 16) |
||
|
(4, 5, 6) 15 |
(8, 5, 6) 19 |
Выигрыш игрока I при ходе (16, 5, 6) |
|
|
(4, 10, 6) 20 |
Выигрыш игрока I при ходе (4, 20, 6) |
||
|
(4, 5, 12) 21 |
Выигрыш игрока при ходе (4, 5, 24) |
||
|
(6, 7, 8) 21 |
Выигрыш игрока при ходе (6, 7, 16) |
||
Ответ: при правильной игре выигрывает первый игрок; при этом его первый ход — добавить в каждую кучу по два камня: (2,394) (46,6).
Решение
По теореме Пифагора расстояние от точки А с координатами (х, у) до начала координат равно квадратному корню из суммы квадратов координат: А = .х 2 + у 2 . Чтобы избавиться от вычисления квадратного корня, можно перейти от заданного условия А > 13 к равносильному условию в целых числах: А 2 > 132 = 169.
В начальный момент А 2 = 5 2 + 2 2 = 29, т. е. условие не выполнено.
|
Начальная позиция |
1-й ход первого игрока |
1-й ход второго игрока |
2-й ход первого игрока |
2-й ход второго игрока |
|
(5, 2) 29 |
(8, 2) 68 |
(8, 5) 89 |
(11, 5) 146 |
( 14 , 5) 221 |
|
(8, 8) 128 |
(11, 8) 185 |
|||
|
(8, 9) 145 |
(11, 9) 202 |
|||
|
(5, 5) 50 |
(8,5) 89 |
(11, 5) 146 |
( 14 , 5) 221 |
|
|
(8, 8) 128 |
(11, 8) 185 |
|||
|
(8, 9) 145 |
(11, 9) 202 |
|||
|
(5, 6) 61 |
(8, 6) 100 |
(11, 6) 157 |
(14, 6) 232 |
|
|
(8, 9) 145 |
(11, 9) 202 |
|||
|
(8, 10) 164 |
(11, 10) 221 |
Очевидно, в любом случае выигрывает игрок, который делает второй ход. Таблица содержит все варианты хода первого игрока. Из нее видно, что при любом ходе первого игрока у второго существует ход, приводящий к победе.
Ответ : при правильной игре всегда выигрывает второй игрок.
З. Даны три кучи камней, содержащие соответственно З, 4 и 5 камней. За один ход разрешается или удвоить количество камней в меньшей куче (если таких две, то лишь в одной из них), или добавить 2 камня в большую из куч (если таких две, то лишь в одну из них). Выигрывает игрок, после хода которого во всех трех кучах суммарно становится не менее 23 камней. Игроки ходят по очереди. Выясните, кто выигрывает при правильной игре — первый или второй игрок.
|
Начальная позиция |
1-й ход первого игрока |
1-й ход второго игрока |
2-й ход первого игрока |
2-й ход второго игрока |
|
(3, 4, 5) 12 |
(6, 4, 5) 15 |
(6, 8, 5) 19 |
Выигрыш игрока I при ходе (6, 8, 10) |
|
|
Выигрыш игрока П при ходе игрока I (6, 10, 5) |
||||
|
(8, 4, 5) 17 |
Выигрыш игрока П при любом продолжении игры |
|||
|
(3, 4, 7) 14 |
(6, 4, 7) 17 |
|||
|
(3, 4, 9) 16 |
Выигрыш игрока П при ходе игрока I (6, 4, 9) |
|||
|
Выигрыш игрока I при его ходе (З, 4, 11) и любом дальнейшем ходе игрока П |
||||
Ответ: выигрывает второй игрок; для этого своим первым ходом он должен получить одну из ситуаций: (8,4,5) или (6,4,7).
4. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых З, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в З раза число камней в какой-либо куче, или добавляет 1 камень в какую-либо кучу. Выигрывает игрок, после хода которого обидее число камней в двух кучах становится не менее 16. Кто выигрывает при безошибочной игре — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Решение
Для решения этой задачи составим таблицу (дерево развития игры при различных продолжениях; в обозначениях числа в скобках — количества камней в каждой из двух куч, число после скобок — суммарное количество камней).
|
Начальная позиция |
1-й ход первого игрока (все варианты) |
1-й ход второго игрока (выигрышный ход) |
2-й ход первого игрока (все варианты) |
2-й ход второго игрока (один из вариантов) |
Анализ состояний игры |
|
|
|
|
|
(12, 4) 16 |
Второй игрок выигрывает на четвертом ходе после любого ответа первого игрока (например, утроив число камней в самой большой куче) |
|
(9, 4) 13 |
(27, 4) 31 |
||||
|
(3, 12) 15 |
(3, 36) 39 |
||||
|
|
(3, 15) 18 |
||||
|
|
|
Аналогичные варианты третьего четвертого ходов |
|||
|
(9, 2) 11 |
(27, 2) 29 |
Второй игрок выигрывает ответным ходом |
|||
|
|
(18, 3) 21 |
Второй игрок выигрывает ответным ходом |
|||
Таким образом, выигрывает игрок, который делает второй ход. Таблица содержит все варианты хода первого игрока. Из нее видно, что при любом ходе первого игрока у второго всегда существует ход, приводящий к победе.
Ответ: при правильной игре выигрывает второй игрок, при этом его первый ход должен быть: (4,3), (27, 2) или (18, З).
5.
Выигрывает первый игрок. Своим первым ходом он должен удвоить количество камней во второй куче.
|
Позиция после первого хода |
1-й ход второго игрока |
Выигрышный ход первого игрока |
Анализ состояний игры |
|
(5, 6) 11 |
(10, 6) 16 |
(10, 10) 20 |
Первый игрок выигрывает после любого ответа второго игрока, удвоив число камней в самой большой куче |
|
(9, 6) 15 |
(9, 10) 19 |
Первый игрок выигрывает после любого ответа второго игрока, удвоив число камней в самой большой куче |
|
|
(5, 10) 15 |
(9, 10) 19 или (10, 10) 20 |
Первый игрок выигрывает после любого ответа второго игрока, удвоив число камней в самой большой куче |
|
|
(5, 12) 17 |
(5, 24) 29 |
Выигрыш первого игрока |
Ответ: при правильной игре выигрывает первый игрок; своим первым ходом он должен удвоить количество камней во второй куче.
6. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй — З камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в З раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах СТаН0вится не менее 24. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
|
Начальная позиция |
1-й ход первого игрока |
Выигрышный ход второго игрока |
Анализ состояний игры |
|
|
|
(6, 5) 11 |
Второй игрок выигрывает после любого ответа первого игрока, утроив число камней в самой большой куче |
|
|
(6, 5) 11 |
Второй игрок выигрывает после любого ответа первого игрока, утроив число камней в самой большой куче |
|
|
(12, 3) 15 |
(36, 3) 39 |
Выигрыш второго игрока |
|
|
(4, 9) 13 |
(4, 27) 31 |
Второй игрок выигрывает после любого ответа первого игрока, утроив число камней в самой большой куче |
Ответ: при правильной игре выигрывает второй игрок, поскольку после первого хода первого игрока найдется выигрышный ход второго игрока.
7. Два игрока играют в следующую игру. На координатной плоскости в точке с координатами (О, 1) стоит фишка. Игроки ходят по очереди. Ход состоит в том, что игрок перемещает фишку из точки с координатами (х, у) в одну из трех точек: (х+З, у), (х, у+З) или (х, у+4). Выигрывает игрок, после хода которого расстояние по прямой от фишки до начала координат (О, О) больше 10 единиц. Кто выигрывает — игрок, делающий ход первым, или игрок, делающий ход вторым?
По теореме Пифагора, расстояние от точки А с координатами (х, у) до начала координат равно квадратному корню из суммы квадратов координат: А = х 2 +У 2 . Чтобы избавиться от вычисления квадратного корня, можно перейти от заданного условия А > 10 к равносильному условию в целых числах: А 2 > 10 2 А =112 - 121. В начальный момент А 2 = 0 2 + 1 2 = 1, т. е. условие не выполнено.
|
Позиция после первого хода первого игрока |
1-й ход второго игрока |
2-й ход первого игрока |
Анализ состояний игры |
|
(0, 4) 16 |
(3, 4) 25 |
(6, 4) 52 |
Первый игрок выигрывает, если его второй ход (6, 4), тогда второй игрок не может выиграть вторым ходом |
|
(3, 7) 58 |
|||
|
(3, 8) 73 |
|||
|
(О, 7) 49 |
(3, 7) 58 |
Первый игрок выигрывает |
|
|
(0, 10) 100 |
|||
|
(0, 11) 121 |
|||
|
(0, 8) 64 |
(3, 8) 73 |
Первый игрок выигрывает |
|
|
(0, 11) 121 |
|||
|
(0, 12) 144 |
Ответ: при правильной игре выигрывает первый игрок, для этого на первом ходе ему необходимо получить ситуацию
8. Два игрока играют в следующую игру. Перед ними лежат три кучки камней, в первой из которых 2, во второй — З, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в какой-то куче, или добавляет по два камня в каждую из куч. Выигрывает игрок, после хода которого либо в одной из куч становится не менее 15 камней, либо общее число камней во всех трех кучах становится не менее 25. Кто выигрывает при безошибочной игре обоих игроков игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Решение
|
Позиция после первого хода первого игрока |
1-й ход второго игрока |
Анализ состояний игры |
|
(4, 5, 6) 15 |
(8, 5, 6) 19 |
Первый игрок выигрывает, например, удвоив количество камней в первой куче |
|
(4, 10, 6) 20 |
Первый игрок выигрывает, например, удвоив количество камней во второй куче |
|
|
(4, 5, 12) 21 |
Первый игрок выигрывает, например, удвоив количество камней в третьей куче |
|
|
(6, 7, 8) 21 |
Первый игрок выигрывает, например, удвоив количество камней в третьей куче |
Ответ: при правильной игре выигрывает первый игрок, при этом своим первым ходом он должен добавить по два камня в каждую из куч.
9. Два игрока играют в следующую игру. На координатной плоскости в точке с координатами (1, О) стоит фишка. Игроки ходят по очереди. Ход состоит в том, что игрок перемещает фишку из точки с координатами (х, у) в одну из трех точек: (х+З, у), (х, у+З) или (х, у+4). Выигрывает игрок, после хода которого расстояние по прямой от фишки до начала координат (О, О) больше 13 единиц. Кто выигрывает — игрок, делающий ход первым, или игрок, делающий ход вторым?
Решение
По теореме Пифагора, расстояние от точки А с координатами (х, у) до начала координат равно квадратному корню из суммы квад-
ратов координат: А = .х 2 + у 2 . Чтобы избавиться от вычисления квадратного корня, можно перейти от заданного условия А > 13 к равносильному условию в целых числах: „4 2 > 13 2 А 2 =14 2 = 196. В начальный момент А2 = 1 2 + 0 2 = 1, т. е. условие не выполнено.
Для решения задачи составим таблицу (дерево развития игры при различных продолжениях; в обозначениях числа в скобках — координаты фишки, число после скобок — расстояние от фишки до начала координат).
|
Позиция после первого хода первого игрока |
1-й ход второго игрока |
2-й ход первого игрока (выигрышный ход) |
Анализ состояний игры |
|
(4, 0) 16 |
(4, 3) 25 |
(4, 7) 65 |
Первый игрок выигрывает при любом ходе второго игрока |
|
(7, 0) 49 |
(7, 4) 65 |
||
|
(4, 4) 32 |
(7, 4) 65 или (4, 7) 65 |
Ответ: при правильной игре выигрывает первый игрок, для этого своим первым ходом он должен получить ситуацию (4, О), а затем своим вторым ходом получить одну из ситуаций: (4, 7) или (7, 4).
10. Два игрока играют в следующую игру. Перед ними лежат две кучи камней, в первой из которых З, а во второй — 6 камней. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 2 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 24. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Решение
Выигрывает первый игрок, для этого своим первым ходом он должен получить ситуацию (5, 6). Для доказательства рассмотрим неполное дерево игры после этого хода первого игрока (в обозначениях числа в скобках количества камней в каждой из двух куч, число после скобок — суммарное количество камней).
|
Позиция после первого хода первого игрока |
1-й ход второго игрока |
2-й ход первого игрока (выигрышный ход) |
Анализ состояний игры |
|
(5, 6) 11 |
(7, 6) 13 |
|
Первый игрок выигрывает при любом ответе второго через один ход |
|
(5, 8) 13 |
(7, 8) 15 |
Первый игрок выигрывает при любом ответе второго через один ход |
|
|
(5, 12) 17 |
(5, 24) 29 |
Первый игрок выигрывает |
|
|
(10, 6) 16 |
(20, 6) 26 |
Первый игрок выигрывает |
Ответ: при правильной игре выигрывает первый игрок, для этого своим первым ходом он должен получить ситуацию (5, 6).
Сложность вычисления. Проблема перебора
1. Записано 6 строк, где каждая имеет свой номер — от О до 5. В нулевой строке записана цифра О (нуль). Каждая последующая строка состоит из двух повторений предыдущей и добавленного в конце ее номера (т. е. в г-й строке в конце приписана цифра i). Ниже показаны первые четыре строки, сформированные по описанному правилу (в скобках записаны номера строк):
(1) 001
(2) 0010012
(3) 001001200100123
Решение
Найдем длину последней строки. По условию, длина каждой последующей строки по сравнению с предыдущей увеличивается в 2 раза плюс добавляется еще один символ — цифра, обозначающая порядковый номер строки.
Получается, что длина строк составит:
(0) — 1 элемент в строке;
(1) — 1 • 2 + 1 = З элемента в строке;
7 элементов в строке;
15 элементов в строке;
![]() 1 • 2 + 1 — 31
элемент в строке;
1 • 2 + 1 — 31
элемент в строке;
(5) — 31 • 2 + 1 =63 элемента в строке.
Требуется найти 62-й элемент в строке длиной в 63 символа. Это означает, что нам нужен второй элемент с конца (предпоследний в строке).
Последний символ в последней строке — это ее номер: 5.
Предпоследний элемент строки — это последняя цифра в предыдущей строке (согласно правилу формирования строк). Но окончание предыдущей строки — это ее номер, т. е. цифра 4. Ответ: 4.
2. Цепочки символов (строки) создаются по следующему правиЛУ. Первая строка состоит из одного символа — цифры 1. Каждая из последующих строк создается следующими действиями: в очередную строку дважды записывается предыдущая строка (цепочка цифр, одна за другой, подряд), а в конец приписывается еще одно число — номер строки по порядку (т. е. на i-M шаге дописывается число i). Вот первые 4 строки, созданные по этому правилу:
(2) 112
(3) 1121123
(4) 112112311211234
Решение
Проследим закономерность получения четных цифр в каждой строке.
(1) — О четных цифр в строке;
![]() 1 четная цифра в строке;
1 четная цифра в строке;
![]() 2 четные цифры в
строке;
2 четные цифры в
строке;
(4) — 5 четных цифр в строке...
То есть можно сформулировать следующее правило нахождения количества четных цифр в строке: если порядковый номер строки четный, то количество четных чисел ищется путем увеличения в два раза количества четных чисел в предыдущей строке; если порядковый номер строки нечетный, то количество четных чисел в предыдущей строке необходимо умножить на два и прибавить единицу.
По сформулированному правилу определим количество четных чисел в искомой строке:
![]() 10 четных чисел;
10 четных чисел;
(6) — 21 четное число;
(7) — 42 четных числа;
(8) — 85 четных чисел; (9)— 170 четных чисел. Ответ: 170.
З. Цепочки символов (строки) создаются по следующему правиЛУ. Первая строка состоит из одного символа — цифры 1. Каждая из последующих цепочек создается следующими действиями: вначале записывается число — номер строки по порядку (т. е. для Ьй строки ставится число i), а далее дважды подряд записывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) 211
(3) 3211211
(4) 432112113211211
Сколько раз суммарно встречается цифра 1 в первых семи строках?
Решение
Найдем количество цифр 1, встречающихся в каждой строке. По условию, длина каждой последующей строки по сравнению с предыдущей увеличивается в 2 раза плюс добавляется еще один символ в начале строки — число, обозначающее порядковый номер этой строки. В результате получается, что количество единиц в последующей строке в два раза больше, чем в предыдущей:
![]() 1 единица в строке;
1 единица в строке;
![]() 2 4 единицы в строке;
2 4 единицы в строке;
![]() 4 2 = 8 единиц в строке;
4 2 = 8 единиц в строке;
![]() 8 2 = 16 единиц в строке;
8 2 = 16 единиц в строке;
![]() 16 • 2 = 32 единицы в строке;
16 • 2 = 32 единицы в строке;
(7) — 32 • 2 = 64 единицы в строке.
Сложив полученное количество цифр 1, мы получим искомое их количество:
1 2 +4 +8 + 16 + 32 + 64 = 127 цифр 1. Ответ: 127.
4. Записано 7 строк, каждая имеет свой номер — от О до 6. В начальный момент в строке записана цифра О (нуль). На каждом из последующих 6 шагов выполняется следующая операция: в очередную строку записывается удвоенная предыдущая строка, а в конец этой строки приписывается очередная цифра (т. е. на i-M шаге приписывается цифра i). Для удобства в скобках пишется номер строки (начиная с О). Ниже показаны первые строки, сформированные по описанному правилу:
(1) 001
(2) 0010012
(3) 001001200100123
Какая цифра стоит в последней строке на 123-м месте (считая слева направо)?
Решение
Найдем длину последней строки. По условию, длина каждой последующей строки по сравнению с предыдущей увеличивается в 2 раза плюс добавляется еще один символ — цифра, обозначающая порядковый номер строки.
Получается, что длина строк составит:
![]() 1 элемент в строке;
1 элемент в строке;
![]() 1 2 + 1 = З элемента
в строке;
1 2 + 1 = З элемента
в строке;
(2) З 2 + 1 = 7 элементов в строке;
![]() 7 2 + 1 = 15
элементов в строке;
7 2 + 1 = 15
элементов в строке;
![]() 1 • 2 + 1 = 31 элемент в строке;
1 • 2 + 1 = 31 элемент в строке;
(5) — 31 • 2 + 1 = 63 элемента в строке;
![]() 63 • 2 + 1 = 127 элементов в строке.
63 • 2 + 1 = 127 элементов в строке.
|
N2 символа |
121 |
122 |
123 |
124 |
125 |
|
|
|
Символ |
О |
1 |
2 |
з |
4 |
5 |
6 |
Следовательно, искомый 123-й символ — 2. Ответ: 2.
5. Цепочки символов (строки) создаются по следующему правилу: первая строка состоит из одного символа — цифры 1. Каждая из следующих цепочек создается так: сначала записывается порядковый номер данной строки, а далее дважды записывается вся цепочка цифр из предыдущей строки. Первые 4 строки, созданные по этому правилу, выглядят следующим образом:
1
211
3211211
432112113211211
Сколько раз в общей сложности встречаются в 10-й строке нечетные цифры (1, З, 5, 7 и 9)?
Решение
Проследим закономерность получения нечетных цифр в каждой строке:

То есть можно сформулировать следующее правило нахождения количества нечетных цифр в строке: если порядковый номер строки четный, то количество нечетных чисел ищется путем увеличения в два раза количества нечетных чисел в предыдущей строке; если порядковый номер строки нечетный, то количество нечетных чисел в предыдущей строке необходимо умножить на два и прибавить единицу.
По сформулированному правилу определим количество нечетных чисел в искомой строке:
(5) — 21 нечетное число;
![]() 42 нечетных числа;
42 нечетных числа;
(7) — 85 нечетных чисел;
(8) —
170 нечетных чисел; ![]() 341 нечетное число.
341 нечетное число.
Далее, следует обратить внимание, что в десятой строке появляется двузначное число 10, которое содержит одну нечетную цифру 1. Следовательно, количество нечетных цифр в десятой строке равно 683.
Ответ: 683.
6. Цепочки символов (строки) создаются по следующему правилу: в начальный момент в строке записана цифра О (нуль). На каждом из последующих 9 шагов выполняется следующая операция: в очередную строку дважды записывается предыдущая строка, а в конец этой строки приписывается очередная цифра (т. е. на п-м шаге приписывается цифра п). Ниже показаны первые строки, сформированные по описанному правилу (в скобках записан номер строки начиная с О):
(1) 001
(2) 0010012
(3) 001001200100123
Сколько раз встретится цифра 1 в последней строке? Решение
Найдем количество цифр 1, встречающихся в каждой строке. По условию, длина каждой последующей строки по сравнению с предыдущей увеличивается в 2 раза плюс добавляется еще один символ в начале строки — число, обозначающее порядковый номер этой строки. В результате получается, что количество единиц в последующей строке в два раза больше, чем в предыдущей:

(2) — 1 • 2 = 2 единицы в строке;
(З) — 2 • 2 = 4 единицы в строке;
![]() 4 8 единиц в строке;
4 8 единиц в строке;
![]() 8 2 = 16 единиц в строке;
8 2 = 16 единиц в строке;
(6) — 16 • 2 = 32 единицы в строке;
(7)— 32 • 2 = 64 единицы в строке; ![]() 64 • 2 = 128 единиц в строке; (9) —
128 • 2 = 256 единиц в строке. Ответ: 256.
64 • 2 = 128 единиц в строке; (9) —
128 • 2 = 256 единиц в строке. Ответ: 256.
7. В начальный момент в строке записана цифра О (нуль). На каждом из последующих 9 шагов выполняется следующая операция: в очередную строку дважды записывается предыдущая строка, а в конец строки приписывается очередная цифра (т. е. на i-M шаге приписывается цифра Г). Ниже показаны первые строки, сформированные по описанному правилу (в скобках записан номер строки начиная с О):
(1) 001
(2) 0010012
(3) 001001200100123
Какая цифра стоит в последней строке на 1022-м месте? Решение
Найдем длину последней строки. По условию, длина каждой последующей строки по сравнению с предыдущей увеличивается в 2 раза плюс добавляется еще один символ — число, обозначающее порядковый номер самой строки. В результате получается, что длина строк составит:
![]() 1 элемент в строке;
1 элемент в строке;
![]() 1 • 2 + 1 = З элемента в строке;
1 • 2 + 1 = З элемента в строке;
![]() З 2 + 1 = 7 элементов в строке;
З 2 + 1 = 7 элементов в строке;
(З) 7 2 + 1 = 15 элементов в строке;
(4) — 15 • 2 + 1 = 31 элемент в строке;
(5) — 31 • 2 + 1 = 63 элемента в строке;
![]() 127 элементов в строке;
127 элементов в строке;
255 элементов в строке;
511 элементов в строке;
1023 элемента в строке.
Требуется найти 1022-й элемент в строке длиной в 1023 символа. Это означает, что нам нужен второй элемент с конца (предпоследний в строке). Последний символ в последней строке — это ее номер: 9. Предпоследний элемент строки — это последняя цифра в предыдущей строке (согласно правилу формирования строк), но окончание предыдущей строки — это ее номер, т. е. цифра 8. Ответ: 8.
8. Цепочки символов (строки) создаются по следующему правиЛУ. Первая строка состоит из одного символа — цифры 1. Каждая из следующих цепочек создается так: сначала записывается порядковый номер данной строки, а далее дважды записывается вся цепочка цифр из предыдущей строки. Первые 4 строки, созданные по этому правилу, выглядят следующим образом:
(2) 211
(3) 3211211
(4) 432112113211211
Сколько раз в общей сложности встречается в 9-й строке цифра 1? Решение
(1) 1 единица в строке;
(2) — 1 • 2 = 2 единицы в строке;
![]() — 2 • 2 = 4 единицы в строке;
— 2 • 2 = 4 единицы в строке;
![]() 4 8 единиц в строке;
4 8 единиц в строке;
(5)— 8 2 = 16 единиц в строке;
![]() 16 • 2 = 32 единицы в строке;
16 • 2 = 32 единицы в строке;
(7) — 32 • 2 = 64 единицы в строке.
(8) — 64 • 2 = 128 единиц в строке.
(9) — 128 • 2 = 256 единиц в строке. Ответ: 256.
9. Упаковка информации методом ТАЕ-кодирования состоит в следующем. Упакованная последовательность содержит управляющие байты, где за каждым управляющим байтом следует один или несколько байтов данных. Если старший бит управляющего байта
равен 1, то следующий за этим управляющим байтом байт данных при распаковке нужно повторить столько раз, сколько записано в оставшихся 7 битах управляющего байта. Если же старший бит управляющего байта равен О, то надо взять несколько следующих байтов данных без их изменения, а сколько именно — записано в оставшихся 7 битах управляющего байта. Например, управляющий байт 10000111 говорит о том, что следующий за ним байт надо повторить 7 раз, а управляющий байт 00000100 — о том, что следующие за ним 4 байта надо взять без изменений.
Пусть после кодирования методом RLE получилась следующая последовательность байтов (первый байт — управляющий):
![]()
Сколько байтов будет содержать данная последовательность после ее распаковки? (Запишите только число — количество таких байтов.)
Решение
При выполнении данного задания не нужно распаковывать последовательность, а надо лишь определить ее длину.
![]()
значит, следующий за ним байт должен повторяться. Количество его
![]()
Следовательно, последний байт должен повториться 15 раз. В итоге получаем:
|
управляющий |
байт |
байт П |
байт III |
управляющий |
байты IV-XVIII |
|
00000011 |
|
|
|
|
|
Учитывая, что управляющие байты в получаемую распакованную последовательность уже не входят, после распаковки данная последовательность будет содержать 18 байтов. Ответ: 18.
10. Упаковка информации методом Т,Е-кодирования состоит в следующем. Упакованная последовательность содержит управляющие байты, где за каждым управляющим байтом следует один или несколько байтов данных. Если старший бит управляющего байта равен 1, то следующий за этим управляющим байтом байт данных
6 ДергачеваЛ. М.
при распаковке нужно повторить столько раз, сколько записано в оставшихся 7 битах управляющего байта. Если же старший бит управляющего байта равен О, то надо взять несколько следующих байтов данных без их изменения, а сколько именно — записано в оставшихся 7 битах управляющего байта. Например, управляющий байт 10000111 говорит о том, что следующий за ним байт надо повторить 7 раз, а управляющий байт 00000100 — о том, что следующие за ним 4 байта надо взять без изменений.
Пусть после кодирования методом RLE получилась следующая последовательность байтов (первый байт — управляющий):
![]()
10101010.
Сколько байтов будет содержать данная последовательность после ее распаковки? (Запишите только число количество таких байтов.)
Решение
При выполнении данного задания не нужно распаковывать последовательность, а надо лишь определить ее длину.
Далее идет третий байт управляющий 00000010, начинающийся с цифры О, значит, несколько следующих байтов будут повторяться по одному разу. Количество этих байтов записано в семи
![]()
раз.
Шестой байт управляющий 10000101, начинается с цифры 1, значит, следующий за ним байт должен повторяться. Количество его повторений записано в семи младших битах: 1012 = 5 повторений. Следовательно, последний байт должен повториться 5 раз. В итоге получаем:
|
управляющий |
байты |
управляющий |
байт IV |
байт |
управля- ющий |
байты VI-x |
|
10000011 |
10101010 00000010 |
|
|
|
|
|
Учитывая, что управляющие байты в получаемую распакованную последовательность уже не входят, после распаковки данная последовательность будет содержать 10 байтов.
10.
11. Строки (цепочки латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Ј-я буква алфавита), а к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ААВ
(3) ААВААВС
(4) ААВААВСААВААВС])
Латинский алфавит (для справки):
ABCDEFGHIJKLMNOPQRSTUVWXYZ.
Запишите шесть символов подряд, стоящих в седьмой строке с 117-го по 122-е место (считая слева направо).
Решение
Подсчитаем количество символов, содержащихся в каждой строке:
![]() 1 символ;
1 символ;
(З) З 2 + 1 = 7 символов;
![]() — 15 символов;
— 15 символов;
31 символ;
(6) = 63 символа;
(7) 63 • 2 + 1 —— 127 символов.
Седьмая строка строится так: к первому символу (У слева дважды приписывается шестая строка:
|
(6) |
(6) |
|
Алгоритм построения строк таков, что справа в них накапливаются последовательные символы латинского алфавита. Для седьмой строки это ABCDEFG, стоящие на местах: 121, 122, 123, 124, 125, 126, 127. Следовательно, на 121-м и 122-м местах будут находиться символы А и В.
Перед группой символов ABCDEFG стоит
символ А, которому предшествует группа символов ААВ. Значит, символы 117, 118,
119, 120 найдены— это![]()
Таким образом, с 117-го по 122-е место стоят символы ААВААВ. ААВААВ.
12. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Ј-я буква алфавита), ак ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ВАА
(3) СВААВАА
(4) Г)СВААВААСВААВАА
Латинский алфавит (для справки):
ABCDEFGHIJkLMNOPQRSTUVWXYZ.
Запишите семь символов подряд, стоящие в восьмой строке с 126-го по 132-е место (считая слева направо).
Решение
Подсчитаем количество символов, содержащихся в каждой
строке:
![]() 1 символ;
1 символ;
(2) ![]() 1 2 + символа;
1 2 + символа;
![]() 7 • 2+ 1 = 15
символов;
7 • 2+ 1 = 15
символов;
( 5) ![]() 15 2 1 = 31 символ;
15 2 1 = 31 символ;
![]() (6) 63
символа;
(6) 63
символа;
127 символов;
(8) — 127 2 + 1 = 255 символов.
Восьмая строка строится так: к первому символу Н справа дважды приписывается седьмая строка:
|
н |
(7) |
(7) |
Алгоритм построения строк таков, что слева накапливаются последовательные символы латинского алфавита в обратном порядке, так как первый символ строки сдвигает последующие символы на одну позицию вправо. Следовательно, на 126-м, 127-м и 128-м местах будут находиться символы В, А и А — три последних символа седьмой строки. Далее будет находиться группа символов GFEDCBA, стоящая на 129-м, 130-м, 131-м, 132-м, 133-м, 134-м и 135-м местах. Значит, символы 126, 127, 128, 129, 130, 131, 132 найдены— это BAAGFED.
Таким образом, с 126-го по 132-е место стоят символы BAAGFED. BAAGFED.
13. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется i-$i буква алфавита), а к ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ВАА
(3) СВААВАА
(4) ХВААВААСВААВАА
Латинский алфавит (для справки):
ABCDEFGHIJKLMNOPQRSTUVWXYZ.
Сколько в восьмой строке содержится букв, отличающихся от буквы А?
Решение
Подсчитаем количество символов, содержащихся в восьмой строке:
![]() 1 символ;
1 символ;
![]() 7 символов;
7 символов;
15 символов;
(5) — 15 • 2+1=31 символ;
![]() 63 символа;
63 символа;
127 символов;
(8) — 127 • 2 + 1 = 255 символов.
Первая строка содержит два символа А, а далее количество этих символов увеличивается в два раза. Таким образом, количество сим-
п—1
волов А можно вычислить по формуле 2 , где п — порядковый номер строки. Значит, в восьмой строке содержится 2 8- 1 = 2 7 = 128 символов А.
Для ответа на поставленный в задаче вопрос вычтем из общего количества символов, содержащихся в восьмой строке, количество символов А:
255 — 128 = 127 символов, отличающихся от буквы А. Ответ: 127.
14. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими
действиями: в очередную строку сначала дважды подряд записывается предыдущая строка, а потом справа приписывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется i-5i буква алфавита). Вот первые 4 строки, созданные по этому правилу:
(2) ААВ
(3) ААВААВС
(4) ААВААВСААВААВСГ)
Латинский алфавит (для справки):
ABCDEFGHIJkLMNOPQRSTUVWXYZ.
Запишите шесть символов подряд, стоящих в восьмой строке с 101-го по 106-е место (считая слева направо).
Решение
Подсчитаем количество символов в каждой строке:
З символа;
7 символов;
![]() — 31 символ;
— 31 символ;
63 символа;
(7) — 63 • 2 + 1 —— 127 символов;
![]() 127 • 2 + 1 = 255 символов.
127 • 2 + 1 = 255 символов.
Восьмая строка строится так: к первому символу Н слева дважды приписывается седьмая строка:
|
(7) |
(7) |
н |
|
1 ... 127 |
128 ... 254 |
255 |
Искомые символы находятся в седьмой строке, которая построена следующим образом: к первому символу G слева дважды приписывается шестая строка.
|
(6) |
(6) |
|
|
1 ... 63 |
64 ... 126 |
127 |
То есть необходимые нам символы находятся в шестой строке (в ее второй копии), которая имеет следующий вид:
|
(5) |
(5) |
|
|
|
95 ... 125 |
126 |
Выпишем первые символы пятой строки, среди которых будут и стоящие с 101-го по 106-е место:
|
|
|
|
98 |
99 |
100 |
101 |
102 |
103 |
|
105 |
106 |
107 |
108 |
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
с |
Таким образом, с 101 -го по 106-е место стоят символы СААВАА. Ответ: СААВАА.
15. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Ј-я буква алфавита), а к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2)
(3) ААВААВС
(4) ААВААВСААВААВС])
Латинский алфавит (для справки):
ABCDEFGHIJkLMNOPQRSTUVWXYZ.
Запишите семь символов подряд, стоящих в седьмой строке с 118-го по 124-е место (считая слева направо).
Решение
Подсчитаем количество символов, содержащихся в каждой строке:
(1) — 1 символ;
![]() 1 2 + 1 = З символа;
1 2 + 1 = З символа;
(З) ![]() 7 символов;
7 символов;
![]() 15 символов;
15 символов;
(5)— 15 • 2 + 1 = 31 символ;
(7) —63 • 2 + 1 -— 127 символов.
Седьмая строка строится так: к первому символу G слева дважды приписывается шестая строка:
|
(6) |
(6) |
|
Алгоритм построения строк таков, что справа накапливаются последовательные символы латинского алфавита. Для седьмой строки это ABCDEFG, стоящие на местах 121, 122, 123, 124, 125, 126 и 127. Следовательно, на 121-м, 122-м, 123-м, 124-м местах будут находиться символы А, В, С, 1).
Перед группой символов ABCDEFG стоит символ А, которому предшествует группа символов ААВ. Значит, символы 118, 119, 120 найдены — это АВА.
Таким образом, с 118-го по 124-е место стоят символы АВААВСЕ).
ответ: АВААВСТ
(2) ААБ
(3) ААБААБВ
(4) ААБААБВААБААБВГ
Начальная часть русского алфавита (для справки): АБВГДЕЁЖЗИЙК...
Сколько раз в общей сложности встречаются в восьмой строке
согласные буквы (Б, В, Г, Д, Ж, З, К,![]()
Решение
Подсчитаем количество согласных букв, содержащихся в каждой строке:
(1) — О согласных букв;
![]() 1 согласная буква;
1 согласная буква;
(3) — 1 • 2 + 1 = З согласные буквы (два раза записана буква Б и один раз В);
(4) — З • 2 + 1 = 7 согласных букв (дважды записаны предыдущие строки, затем приписана согласная буква Г);
(5) — 7 • 2 + 1 = 15 согласных букв (дважды записаны предыдущие строки, затем приписана согласная буква Д);
(6)
— 15 • 2 + О = 30
согласных букв (дважды записаны предыдущие строки, затем приписана гласная
буква Е); ![]()
(7) — 30 • 2 + О = 60 согласных букв (дважды записаны предыдущие строки, затем приписана гласная буква Ё);
(8) — 60 • 2 + 1 = 121 согласная буква (дважды записаны предыдущие строки, затем приписана согласная буква Ж).
Таким образом, в общей сложности согласные буквы встречаются в восьмой строке 121 раз. Ответ: 121.
17. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется i-51 буква алфавита), а к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ААВ
(3) ААВААВС
(4) ААВААВСААВААВС1)
Латинский алфавит (для справки):
Запишите шесть символов подряд, стоящие в седьмой строке с 120-го по 125-е место (считая слева направо).
Решение
Подсчитаем количество символов, содержащихся в каждой строке:
![]() 1 символ;
1 символ;
(2) 1 2 + 1 = З символа;
(3)— З • 2 + 1 = 7 символов;
![]() 7 2 + 1 = 15 символов;
7 2 + 1 = 15 символов;
(5) — 15 • 2+ 1 = 31 символ;
![]() 31 • 2 + 1 = 63 символа;
31 • 2 + 1 = 63 символа;
(7)— 63 • 2 + 1 = 127 символов.
Седьмая строка строится так: к первому символу G слева дважды приписывается шестая строка:
|
(6) |
(6) |
|
Алгоритм построения строк таков, что справа накапливаются последовательные символы латинского алфавита. Для седьмой строки это буквы ABCDEFG, стоящие на местах 121, 122, 123, 124, 125, 126, 127. Следовательно, на 121-м, 122-м, 123-м, 124-м местах будут находиться символы А, В, С, 1).
Перед группой символов ABCDEFG стоит символ А, которому предшествует группа символов ААВ. Значит, символы 118, 119, 120 найдены — это АВА.
Таким образом, с 118-го по 124-е место стоят символы ABAABCD.
Ответ: АВА АВСТ
18. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Ј-я буква алфавита), а к ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ВАА
(3) СВААВАА
(4)
Латинский алфавит (для справки):
ABCDEFGHIJkLMNOPQRSTUVWXYZ.
Сколько в восьмой строке содержится букв, отличающихся от буквы В?
Решение
Подсчитаем количество букв В, содержащихся в восьмой строке:
(1) — О букв В;
![]() 1 буква В;
1 буква В;
(3) — 2 буквы В;
(4) 4 буквы В;
(5) 8 букв В;
(6) 16 букв В;
(7) 32 буквы В;
(8) — 64 буквы В.
Подсчитаем общее количество символов, содержащихся в восьмой строке:
(1) 1 символ;
(2)
![]() З символа;
З символа;
7 символов;
15 символов;

Найдем количество букв, отличающихся от буквы В:
255 — 64 = 191 буква.
Таким образом, в восьмой строке содержится 191 буква, отличающихся от буквы В. Ответ: 191.
19. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется ј-я буква алфавита), а к ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ВАА
(3) СВААВАА
(4) И)СВААВААСВААВАА
Латинский алфавит (для справки):
ABCDEFGHIJkLMNOPQRSTUVWXYZ.
Сколько содержится букв С в седьмой строке?
Решение
Подсчитаем количество букв С, содержащихся в восьмой строке:
![]() О букв С;
О букв С;
![]() О букв С;
О букв С;
![]() 1 буква С;
1 буква С;
![]() 1 2 = 2 буквы С;
1 2 = 2 буквы С;
![]() 2 2=4 буквы С;
2 2=4 буквы С;
(6) —4 8 букв С;
![]() 8 2 16 букв С.
8 2 16 букв С.
Таким образом, в седьмой строке содержится 16 букв С. Ответ: 16.
20. Строки (цепочки латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Г-я буква алфавита), а к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ААВ
(3) ААВААВС
(4) ААВААВСААВААВС1)
Латинский алфавит (для справки):
ABCDEFGHIJKLMNOPQRSTUVWXYZ.
Запишите шесть символов подряд, стоящих в восьмой строке с 72-го по 77-е место (считая слева направо).
Решение
Подсчитаем количество символов в каждой строке:
![]() 1 символ;
1 символ;
(2) — 1 • 2 + 1 = З символа;
(3) 7 символов;
(4) 15 символов;
(5)
(6) — 31 • 2 + 1 -— 63 символа;
![]() 127 символов;
127 символов;
(8) — 127 • 2+ 1 = 255 символов.
Восьмая строка строится так: к первому символу Н слева дважды приписывается седьмая строка:
|
(7) |
(7) |
н |
|
1 ... 127 |
128 ... 254 |
255 |
Искомые символы находятся в седьмой строке, которая построена следующим образом: к первому символу (А слева дважды приписывается шестая строка.
|
(6) |
(6) |
|
|
1 ... 63 |
64 ... 126 |
127 |
То есть необходимые нам символы находятся в шестой строке (в ее второй копии), которая имеет вид:
|
(5) |
(5) |
|
|
64 ... 94 |
95 ... 125 |
126 |
Выпишем первые символы пятой строки, среди которых будут и стоящие с 72-го по 77-е место:
|
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
|
|
|
|
|
|
|
|
|
|
|
|
А |
в |
с |
Таким образом, с 72-го по 77-е место стоят символы АВААВС. ответ: АВААВС.
21. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т.е. на i-M шаге пишется i-$i буква алфавита), а к ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2)
(3) СВААВАА
(4) 1)СВААВААСВААВАА
Латинский алфавит (для справки):
ABCDEFGHIJkLMNOPQRSTUVWXYZ. Запишите шесть символов подряд, стоящих в восьмой строке с 62-го по 67-е место (считая слева направо).
Решение
Подсчитаем количество символов в каждой строке:
![]() 1 символ;
1 символ;
(2) 1 2+ символа;
![]() 7 символов;
7 символов;
15 символов;
31 символ;
31 • 2+1=63 символа;
127 символов;
(8) — 127 • 2 + 1 = 255 символов.
Восьмая строка строится так: к первому символу Н справа дважды приписывается седьмая строка:
|
н |
(7) |
(7) |
|
1 |
2 ... 128 |
129 ... 255 |
Искомые символы находятся в седьмой строке, которая построена следующим образом: к первому символу G слева дважды приписывается шестая строка.
|
|
(6) |
(6) |
|
2 |
з... 65 |
66 ... 128 |
То есть необходимые нам символы находятся в шестой строке, которая имеет следующий вид:
|
|
(5) |
(5) |
|
(5) |
(5) |
|
з |
4 34 |
|
66 |
67 ... 97 |
98 ... 128 |
|
62 |
63 |
64 |
65 |
|
|
|
в |
|
|
|
Таким образом, с 62-го по 67-е место стоят символы ABAAFE. ответ: ABAAFE.
22. Строки (цепочки латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Г-я буква алфавита), а к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ДАВ
(3) ААВААВС
(4) ААВААВСААВААВС1)
Латинский алфавит (для справки):
ABCDEFGHIJKLMNOPQRSTUVWXYZ.
Запишите шесть символов подряд, стоящих в восьмой строке с 100-го по 105-е место (считая слева направо).
Решение
Подсчитаем количество символов в каждой строке:
![]() 1 символ;
1 символ;
(2) 1 2 + символа;
![]() 7 символов;
7 символов;
15 символов;
1 31 символ;
63 символа;
127 символов;
(8) 127 • 2 + 1 = 255 символов.
Восьмая строка строится так: к первому символу Н слева дважды приписывается седьмая строка:
|
(7) |
(7) |
н |
|
1 . .. 127 |
128 .. . 254 |
255 |
|
(6) |
(6) |
|
|
1 . . . 63 |
64 . . . 126 |
127 |
То есть необходимые нам символы находятся в шестой строке (в ее второй копии), которая имеет вид:
|
(5) |
(5) |
|
|
64 ... 94 |
95 ... 125 |
126 |
Выпишем первые символы пятой строки, среди которых будут и стоящие с 100-го по 105-е место:
|
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, с 100-го по 105-е место стоят символы ВСААВА. Ответ: ВСААВА.
23. Строки (цепочки русских букв) создаются по следующему правилу. Первая строка состоит из одного символа — русской буквы А.
Каждая из последующих строк создается такими действиями: в оче-
редную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Г-я буква алфавита), а к ней слева дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ААБ
(3) ААБААБВ
(4) ААБААБВААБААБВГ
Начальная часть русского алфавита (для справки):
АБВГДЕЁЖЗИКЛ![]()
Сколько раз в общей сложности встречаются в седьмой строке гласные буквы (А, Е, Ё, И, ...р
Решение
Подсчитаем количество гласных букв, содержащихся в каждой строке:
![]() 1 гласная буква;
1 гласная буква;
(2) — 1 2 = 2 гласные буквы;
![]() 2 2 = 4 гласные буквы;
2 2 = 4 гласные буквы;
(4) — 4 • 2 = 8 гласных букв;
(5)
(6) 16 • 2 + 1 = 33 гласные буквы;
(7) — 33 • 2 + 1 = 67 гласных букв.
Таким образом, в общей сложности гласные буквы встречаются в седьмой строке 67 раз. Ответ: 67.
24. Строки (цепочки символов латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа — латинской буквы А. Каждая из последующих строк создается такими действиями: в очередную строку сначала записывается буква, порядковый номер которой в алфавите соответствует номеру строки (т. е. на i-M шаге пишется Ј-я буква алфавита), а к ней справа дважды подряд приписывается предыдущая строка. Вот первые 4 строки, созданные по этому правилу:
(2) ВАА
(3) СВААВАА
(4) И)СВААВААСВААВАА
Латинский алфавит (для справки):
ABCDEFGHIJKLMNOPQRSTUVWXYZ. Сколько в восьмой строке содержится букв А?
Решение
Ответ: 128.
Элементы теории алгоритмов
1. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз С, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
![]() НАЧАЛО
НАЧАЛО
6
ПОКА <снизу свободно вниз
ПОП «(слева свободно влево5 ПОКА сверху свободно вверх4
КОНЕЦз
2
1
![]()
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетка F4 соответствует необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку по условию задачи движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вправо, необходимым условием для искомой начальной клетки является наличие границы справа — эта граница не позволит РОБОТУ продвинуться правее начального положения, если он в него попадет. Таких клеток с границей справа имеется 10: А 1, В2, Сб, Е5, F1, F2, F3, F4, F5, F6.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
А1-А5-Е5 |
|
|
|
В2-В1-В4-Р4 |
|
|
|
-А4-А5-Е5 |
|
|
|
E5-E2-C2-C3-F3 |
|
|
|
F1-B1-B4-F4 |
|
|
|
F2-F1-B1-B4-F4 |
|
|
|
F3-F1-B1-B4-F4 |
|
|
|
F4-F1-B1-B4-F4 |
|
|
|
F5-F1-B1-B4-F4 |
|
|
|
F6-F1-B1-B4-F4 |
|
Таким образом, искомая клетка одна.
Номер ответа: 1.
2. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ф, влево е, вправо —». Еще
![]()
четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится и программа прервется.
![]() Сколько клеток
приведенного лаби-
Сколько клеток
приведенного лаби-
ринта соответствуют требованию, что, вы-6
полнив предложенную ниже программу,
5 РОБОТ остановится в той же клетке, с которой он начал движение?4
НАЧАЛОз
ПОКА «верху свободно> вправо
2
ПОКА <слева свободно> вверх
КОНЕЦ
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетка В4 соответствует необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вверх, необходимым условием для искомой начальной клетки является наличие границы слева — эта граница не позволит РОБОТУ продвинуться выше начального положения, если он в него попадет. Однако при отсутствии границы слева РОБОТ разрушится, поскольку продолжит движение в сторону стены. Поэтому следует рассматривать клетки, имеющие границы сверху и слева. Таких клеток З: Аб, В4, (Л.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
Аб |
Аб-А4, разрушение |
|
|
|
В4-В1-В4 |
|
|
|
С1, разрушение |
|
Таким образом, искомая клетка одна. Номер ответа: 1.
З. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости: вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ш, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
Цикл
ПОП <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
![]() НАЧАЛО
НАЧАЛО
5
ПОП <слева свободно> влево
ПОП <снизу свободно вниз4
КОНЕЦз
2
1
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки А 1, Аб, С1 и D3 соответствуют необходимому требованию.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
|
|
|
Аб |
Аб-С6-А6 |
Аб |
|
|
D3-F3-F6-D6-D3 |
|
Таким образом, искомых клеток три. Номер ответа: З.
4. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:
Вперед п (где п — целое число) — вызывает передвижение Черепашки на п шагов в направлении движения.
Направо т (где т — целое число) — вызывает изменение направления движения на т градусов по часовой стрелке.
Запись Повтори К [Команда 1 Команда 2 Команда З] означает, что последовательность команд в скобках повторится К раз.
Черепашке был дан для исполнения следующий алгоритм: Повтори 10 [Направо 36 Вперед 20 Направо 36)
Какая фигура появится на экране?
1) Правильный пятиугольник
2) Правильный шестиугольник
З) Правильный десятиугольник 4) Незамкнутая ломаная линия Решение
Изобразим фигуру, которая появится на экране.
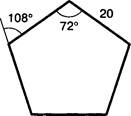
Кроме того, можно
воспользоваться формулой (п — 2) • 180 0 = ![]() 108 0 ,
где п — количество сторон правильного п-угольника. Получим, что п = 5.
108 0 ,
где п — количество сторон правильного п-угольника. Получим, что п = 5.
Номер ответа: 1.
Вперед п (где п — целое число) — вызывает передвижение Черепашки на п шагов в направлении движения.
Направо п (где т — целое число) — вызывает изменение направления движения на т градусов по часовой стрелке.
Запись Повтори К [Команда 1 Команда 2 Команда З] означает, что последовательность команд в скобках повторится К раз.
Черепашке был дан для исполнения следующий алгоритм: Повтори 5 [Вперед 10 Направо 72] Какая фигура появится на экране?
1) Незамкнутая ломаная линия 2) Правильный треугольник
З) Правильный десятиугольник 4) Правильный пятиугольник
Решение
Изобразим фигуру, которая появится на экране.
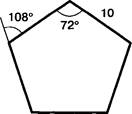
Кроме того, можно воспользоваться формулой (п — 2) • 1800 = — 108 0 , где п — количество сторон правильного п-угольника. Получим, что п = 5.
Номер ответа: 4.
6. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ш, влево е, вправо Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
НАЧАЛО
5
ПОКА оправа свободно> вправо
КОНЕЦ
з
2
1
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскос-
ти, в ходе которого выясняется, что только клетки Аб, Сб, F6 соотВУГСТВУЮТ необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вверх, необходимым условием для искомой начальной клетки является наличие границы сверху — эта граница не позволит РОБОТУ продвинуться выше начального положения, если он в него попадет. Таких клеток с границей сверху 11: Аб, Вб, Сб, 06, Вб, F6, М, М, СЗ, D2, Е1. Однако из них только клетки Аб, Сб, F6 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
А5-А1-А5 |
|
|
|
Сб-А6-С6 |
|
|
|
F6-D6-D3-F3-F6 |
|
7. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ш, влево е, вправо —». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
![]()
![]() НАЧАЛО
НАЧАЛО
6
ПОКА оправа свободно> вправо5 ПОКА «верху свободно> вверх4
ПОКА <слева свободно> влево
КОНЕЦз
2
1
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки Аб, Аб, D6 соответствуют необходимому требованию.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
А5-А1-А5 |
|
|
Аб |
Аб-С6-А6 |
|
|
|
D6-D3-F3-F6-D6 |
|
Таким образом, искомых клеток три. Номер ответа: З.
8. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ш, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится и программа прервется.
![]() Сколько клеток
приведенного лабиринта соответствуют требованию, что, вы-6
Сколько клеток
приведенного лабиринта соответствуют требованию, что, вы-6
полнив предложенную ниже программу,
НАЧАЛОз
ПОКА «верху свободно> вправо
2
ПОКА <справа свободно> вниз
ПОКА <сниву свободно> влево1
ПОКА <слева свободно> вверх
КОНЕЦ
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки Вб и С5 соответствуют необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, необходимым условием для искомой начальной клетки является наличие границы слева — эта граница не позволит РОБОТУ продвинуться выше начального положения, если он в него попадет. Таких клеток с границей слева 9: А 1, А2, АЗ, А4, Аб, Аб, Вб, С5, F2. Однако из них только клетки Вб и С5 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
Вб-В5-В6 |
|
|
|
С5-Е5-Е2-С2-С5 |
|
Таким образом, искомых клеток две. Номер ответа: 2.
9. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ш, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится
и программа прервется.
![]() Сколько клеток
приведенного лаби-
Сколько клеток
приведенного лаби-
ринта соответствуют требованию, что, вы-6 полнив предложенную ниже программу,5 РОБОТ остановится в той же клетке, с которой он начал движение?4
НАЧАЛОз
ПОКА Оправа свободно> вниз2
ПОП <снизу свободно> влево
1
ПОКА «верху свободно> вправо
КОНЕЦ
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки Вб, D3, Е5 соответствуют необходимому требованию.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
Вб-В5-В6 |
|
|
|
D3-A3-D3 |
|
|
|
Е5-Е2-С2-С5-Е5 |
|
Таким образом, искомых клеток три. Номер ответа: З.
10. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Щ, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
цикл
ПОП <условие> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится и программа прервется.
![]() Сколько клеток
приведенного лаби-
Сколько клеток
приведенного лаби-
6 ринта соответствуют требованию, что, вы-
полнив предложенную ниже программу,5 РОБОТ остановится в той же клетке, с ко-4 торой он начал движение?
НАЧАЛОз
ПОКА <снизу свободно> влево
2
ПОКА <слева свободно> вверх
КОНЕЦ
Решение
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, необходимым условием для искомой начальной клетки является наличие границы справа — эта граница не позволит РОБОТУ продвинуться ниже начального положения, если он в него попадет. Таких клеток с границей справа 9: F1, F2, F3, F4, F5, F6, Е2, В5, Аб. Однако из них только клетки В5, Е2, F3 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
В5-В6-В5 |
|
|
|
Е2-С2-С5-Е5-Е2 |
|
|
|
F3-A3-F3 |
|
Таким образом, искомых клеток три. Номер ответа: З.
11. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх
вниз
влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз ф, влево е, вправо —». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ ОСтИНОвится в той же клетке, с которой он начал движение?
НАЧАЛО
|
|
|
|
|
|
ПОКА <сниву свободно> вниз5
ПОКА <слева свободно> влево
4
КОНЕЦ
З
2
1
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки А 1 и В5 соответствуют необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения влево, необходимым условием для искомой начальной клетки является наличие границы слева — эта граница не позволит РОБОТУ продвинуться левее начального положения, если он в него попадет. Таких клеток с границей слева 11: А 1, А2, АЗ, М, Аб, Аб, А7, Вб, D3, D6, F4. Однако из них только клетки А 1 и В5 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
А1-АЗ-СЗ-С1-А1 |
|
|
|
В5-В6-С6-С5-В5 |
|
Таким образом, искомых клеток две. Номер ответа: 2.
12. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ф, влево е, вправо Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
Цикл
ПОП <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится
и программа прервется.
![]() Сколько клеток приведенного лабиринта соответствуют
требованию, что, вы-6 полнив предложенную ниже программу,5 РОБОТ остановится в
той же клетке, с которой он начал движение?4
Сколько клеток приведенного лабиринта соответствуют
требованию, что, вы-6 полнив предложенную ниже программу,5 РОБОТ остановится в
той же клетке, с которой он начал движение?4
НАЧАЛОз
ПОП <сверху свободно> вправо2
ПОП справа свободно> вниз
ПОП <сниву свободно влево1
ПОКА «слева свободно вверх
КОНЕЦ
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетка В4 соответствует необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, необходимым условием для искомой начальной клетки является наличие границы слева — эта граница не позволит РОБОТУ продвинуться выше начального положения, если он в него попадет. Таких клеток с границей слева 9: А 1, А2, АЗ, М, А5, Аб, В4, С1, Сб. Однако из них только клетка В4 соответствует условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
В4-В1-В4 |
|
Таким образом, искомая клетка одна. Номер ответа: 1.
Вперед п, где п — целое число — вызывает передвижение черепашки на п шагов в направлении движения;
Направо т, где п — целое число — вызывает изменение направления движения на т градусов по часовой стрелке.
Запись Повтори 5 [Команда 1 Команда2) означает, что последовательность команд в скобках повторится 5 раз.
Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [Повтори 4 [Вперед 40 Направо 90] Направо 120]
Какая фигура появится на экране?
1) 2) 3) 4)

7 ДергачеваЛ. М.
В результате выполнения алгоритма Повтори 4 [Вперед 40 Направо 90] на экране появится квадрат. Далее направление движения будет изменено на 120 0 . Затем снова будет нарисован квадрат и произойдет изменение направления движения. После этого будет нарисован еще один квадрат и произойдет изменение направления движения. Таким образом, на экране появится фигура под номером З. Последующие действия не изменят внешний вид полученной фигуры, поскольку Черепашка будет передвигаться по уже имеющемуся изображению.
Номер ответа: З.
14. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
сверху свободно снизу свободно слева свободно справа свободно Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится
и программа прервется.
![]() Сколько клеток приведенного лаби-6 ринта соответствуют
требованию, что, вы-
Сколько клеток приведенного лаби-6 ринта соответствуют
требованию, что, вы-
5 полнив предложенную ниже программу,
РОБОТ остановится в той же клетке, с ко-4 торой он начал движение?
НАЧАЛОз
1
ПОКА <слева свободно> вниз
ПОКА <сниву свободно> вправо
КОНЕЦ
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки В2, С4, D5, Е2 соответствуют необходимому требованию.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
В2-А2-В2 |
|
|
|
С4-С5-В5-В4-С4 |
04 |
|
|
D5-D6-D5 |
|
|
|
Е2-С2-Е2 |
|
Таким образом, искомых клеток четыре. Номер ответа: 4.
15. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ф, влево е, вправо —». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится и программа прервется.
![]() Сколько клеток
приведенного лаби-
Сколько клеток
приведенного лаби-
6 ринта соответствуют требованию, что, вы-
полнив предложенную ниже программу,5 РОБОТ остановится в той же клетке, с ко-
4 торой он начал движение?
НАЧАЛОз ПОКА «верху свободно> вправо2
ПОКА <справа свободно вниз
ПОКА <слева свободно> вверх
КОНЕЦ
Решение
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, необходимым условием для искомой начальной клетки является наличие границы слева — эта граница не позволит РОБОТУ продвинуться выше начального положения, если он в него попадет. Таких клеток с границей слева 13: М, А2, АЗ, М, Аб, Аб, ВЗ, СЗ, C5, D4, Е1, Вб, F4. Однако из них только клетки С5 и Еб соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
05 |
С5-С4-С5 |
05 |
|
|
Еб-Е4-Е6 |
|
Таким образом, искомых клеток две. Номер ответа: 2.
16. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ф, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
ПОКА <слева свободно> влево
ПОП <снизу свободно вниз5 ПОКА <справа свободно> вправо4
КОНЕЦ з
2
1
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки В1 и F1 соответствуют необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вправо, необходимым условием для искомой начальной клетки является наличие границы справа — эта граница не позволит РОБОТУ продвинуться правее начального положения, если он в него попадет. Таких клеток с границей справа 12: F1, F2, F3, F4, F5, F6, Е2, D3, C4, В1, Вб, А5. Однако из них только клетки В1 и F1 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
В1-ВЗ-АЗ-А1-В1 |
|
|
|
F1-F4-D4-D1-F1 |
|
Таким образом, искомых клеток две. Номер ответа: 2.
17. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
![]() Сколько клеток приведенного лабиринта соответствуют
требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той
же клетке, с которой он начал движение?
Сколько клеток приведенного лабиринта соответствуют
требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той
же клетке, с которой он начал движение?
НАЧАЛО
ПОКА справа свободно> вправо
ПОКА «верху свободно> вверх ПОКА <слева свободно влево
ПОКА <снизу свободно вниз
КОНЕЦ

При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки А 1, Аб, D3 соответствуют необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вниз, необходимым условием для искомой начальной клетки является наличие границы снизу — эта граница не позволит РОБОТУ продвинуться ниже начального положения, если он в него попадет. Таких клеток с границей снизу 11: А1, В1, C1, Т, Е1, F1, Аб, В5, C4, 03, Е2. Однако из них только клетки А 1, Аб, D3 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
|
|
|
|
Аб-С6-А6 |
|
|
|
D3-F3-F6-D6-D3 |
|
Таким образом, искомых клеток три. Номер ответа: З.
18. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости: вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз ф, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится и программа прервется.
![]() Сколько клеток
приведенного лаби-
Сколько клеток
приведенного лаби-
6 ринта соответствуют требованию, что, вы-
полнив предложенную ниже программу,5 РОБОТ остановится в той же клетке, с ко-
4 торой он начал движение? з
НАЧАЛО
ПОП «лева свободно> вниз1
ПОП <снизу свободно вправо
ПОП <справа свободно> вверх
КОНЕЦ
Решение
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, необходимым условием для искомой начальной клетки является наличие границы справа — эта граница не позволит РОБОТУ продвинуться выше начального положения, если он в него попадет. Таких клеток с границей справа 10: F1, F2, F3, F4, F5, F6, ЕЗ, С2, С5, М. Однако из них только клетки С5, ЕЗ, F5 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
05 |
С5-В5-В4-С4-С5 |
|
|
ЕЗ |
E3-D3-D2-E2-E3 |
ЕЗ |
|
|
F5-D5-F5 |
|
Таким образом, искомых клеток три.
Номер ответа.![]()
19. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз С, влево е, вправо -». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
![]()
![]() НАЧАЛО
НАЧАЛО
6
ПОКА <сниву свободно> вниз4
ПОП <справа свободно> вправо
КОНЕЦз 2
1
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки М, Е5, F1 соответствуют необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя
команда алгоритма предполагает возможность движения вправо, необходимым условием для искомой начальной клетки является наличие границы справа эта граница не позволит РОБОТУ продвинуться правее начального положения, если он в него попадет. Таких клеток с границей справа 11: F1, F2, F3, F4, F5, F6, А1, В2, СЗ, D4, Е5. Однако из них только клетки А 1, Е5, F1 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
|
|
|
|
Е5-Е6-А6-А5-Е5 |
|
|
|
F1-B1-F1 |
|
Таким образом, искомых клеток три. Номер ответа: З.
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз С, влево е, вправо —». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?

При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки А 1, Аб, В1, F2 соответствуют необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вниз, необходимым условием для искомой начальной клетки является наличие границы снизу — эта граница не позволит РОБОТУ продвинуться ниже начального положения, если он в него попадет. Таких клеток с границей снизу 12: А1, Аб, В1, В5, С1, С4, D1, D3, Е1, Е2, F1, F2. Однако из них только клетки А 1, Аб, В1, F2 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
А1-А5-А1 |
|
|
Аб |
Аб-Е6-А6 |
Аб |
|
|
В1-Р1-В1 |
|
|
|
F2-F6-F2 |
|
Таким образом, искомых клеток четыре.
Номер ответа: 4.
21. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости: вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз ф, влево е, вправо Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
![]()
![]() НАЧАЛО
НАЧАЛО
ПОП <снизу свободно вниз
ПОП <слева свободно> влево
ПОКА «верху свободно> вверх
КОНЕЦ
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки D4 и Еб соответствуют необходимому требованию.
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вправо, необходимым условием для искомой начальной клетки является наличие границы справа — эта граница не позволит РОБОТУ продвинуться правее начального положения, если он в него попадет. Таких клеток с границей справа 11: А2, ВЗ, С5, D4, Еб, F1, F2, F3, F4, F5, F6. Однако из них только клетки D4 и Еб соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
D4-A4-D4 |
|
|
|
Еб-Е2-В2-В6-Е6 |
|
Таким образом, искомых клеток две. Номер ответа: 2.
22. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ф, влево е, вправо —». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
Цикл
ПОКА <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
НАЧАЛО
![]() ПОКА <справа свободно> вправо6
ПОКА <справа свободно> вправо6
ПОКА <снизу свободно вниз
ПОП <.слева свободно влево5
ПОП «(сверху свободно вверх4
КОНЕЦ з 2
1
Решение
При выполнении данного задания возможно последовательное выполнение предложенной программы для всей клетчатой плоскости, в ходе которого выясняется, что только клетки Аб, В5, ЕЗ соответствуют необходимому требованию.
![]()
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
A6-F6-F1-A1-A6 |
Аб |
|
|
В5-С5-С4-В4-В5 |
|
|
ЕЗ |
ЕЗ |
ЕЗ |
Таким образом, искомых клеток три. Номер ответа: З.
23. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх вниз влево вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Щ, влево е, вправо —». Еще четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно снизу свободно слева свободно справа свободно
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
![]()
![]() НАЧАЛО
НАЧАЛО
ПОП «верху свободно> вверх
ПОКА <слева свободно> влево
ПОКА <.сниву свободно> вниз
ПОКА «права свободно> вправо
КОНЕЦ
Решение
Можно оптимизировать алгоритм поиска необходимых клеток лабиринта. Поскольку, по условию задачи, движение РОБОТА должно закончиться в той же клетке, где оно началось, а последняя команда алгоритма предполагает возможность движения вправо, необходимым условием для искомой начальной клетки является наличие границы справа — эта граница не позволит РОБОТУ продвинуться правее начального положения, если он в него попадет. Таких клеток с границей справа 12: F1, F2, F3, F4, F5, F6, Е2, D3, С4, В1, Вб, А5. Однако из них только клетки В1 и F1 соответствуют условию задачи.
|
Начальная клетка |
Перемещения |
Конечная клетка |
|
|
В1-ВЗ-АЗ-А1-В1 |
|
|
|
F1-F4-D4-D1-F1 |
|
Таким образом, искомых клеток две.
![]()
Языки программирования
1. Определите значение переменной а после исполнения данного алгоритма. а 8;
![]()
Порядок действий соответствует правилам арифметики. В ответе укажите одно число — значение переменной а.
Решение
Составим и заполним таблицу:
|
Команда присваивания |
Значение а |
Значение Ь |
|
8 |
8 |
|
|
з |
8 |
зо |
|
|
80 |
зо |
Ответ: 80.
2. Определите значение переменной а после исполнения данного алгоритма.
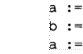
Порядок действий соответствует правилам арифметики. В ОТВете укажите одно число — значение переменной а.
Решение
Составим и заполним таблицу:
|
Команда присваивания |
Значение а |
Значение Ь |
|
4 |
4 |
|
|
Ь 8 + 2 а |
4 |
16 |
|
а |
32 |
|
Ответ.• 32.
![]()
З. переменной с после выполнения следующего фрагмента программы.
![]() - 5;
- 5;
с![]()
![]()
4) с = 33
Решение
Составим и заполним таблицу:
|
Команда присваивания |
Значение а |
Значение Ь |
Значение с |
|
5 |
5 |
|
|
|
а |
11 |
|
|
|
|
11 |
-11 |
|
|
с 2*b; |
11 |
-11 |
33 |
Номер ответа: 4.
4. Определите значение целочисленных переменных а и Ь после выполнения фрагмента программы:
![]() (а div 10) + 14 ;
(а div 10) + 14 ;
![]() (Ь mod 10)
(Ь mod 10)![]()
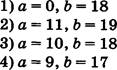
Решение
Составим и заполним таблицу:
|
|
Команда присваивания |
Значение а |
Значение Ь |
|
|
|
35 |
|
|
Ь |
(а div 10) |
35 |
17 |
|
|
(Ь mod 10) 2 |
9 |
17 |
![]()
210
![]()
5. а и Ь после выполнения фрагмента программы:
![]()
![]() (а div 100) * 10 + 9;
(а div 100) * 10 + 9; ![]()
![]() (10 * Ь — а) mod 100;
(10 * Ь — а) mod 100;
71, Ь- 199
4)а - 71, Ь- 189
Решение
Составим и заполним таблицу:
|
|
Команда присваивания |
Значение а |
Значение Ь |
|
а |
|
1819 |
|
|
Ь |
(а div 100) * 10 + 9 |
1819 |
189 |
|
|
а) mod 100 |
71 |
189 |
Номер ответа: 4.
6. Определите значение целочисленных переменных а и Ь после выполнения фрагмента программы: а 42;
![]() 14
; а а div Ь;
14
; а а div Ь;

З) а- О, Ь- 588
![]() 14, Ь- 42
14, Ь- 42
Решение
Составим и заполним таблицу:
|
|
Команда присваивания |
Значение а |
Значение Ь |
|
а |
42 |
42 |
|
|
Ь |
14 |
42 |
14 |
|
|
а div |
з |
14 |
|
Ь |
а |
з |
42 |
|
|
Ь div |
14 |
42 |
![]()
![]()
7. х, и t после выполнения фрагмента
программы: х![]()
![]() у mod х;
у mod х;
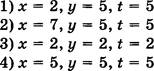
Решение
Составим и заполним таблицу:
|
Команда присваивания |
Значение х |
Значение у |
Значение t |
|
х 5 |
5 |
|
|
|
7 |
5 |
7 |
|
|
|
5 |
7 |
5 |
|
х У mod х |
2 |
7 |
5 |
|
|
2 |
5 |
5 |
Номер ответа: 1.
8. Определите
значение целочисленных переменных а и Ь после выполнения фрагмента программы: а![]()
![]() (Ь mod 10)
(Ь mod 10)
Решение
Составим и заполним таблицу:
|
|
Команда присваивания |
Значение а |
Значение Ь |
|
а |
|
75 |
|
|
Ь |
(а div 10) 5 |
75 |
12 |
|
|
(Ь mod 10) 1 |
З |
12 |
![]()
212
![]()
9. х и после выполнения фрагмента программы:
![]() 336;
336; ![]() 8;
8;
![]()

Решение
Составим и заполним таблицу:
|
|
Команда присваивания |
Значение х |
Значение у |
|
|
- 336 |
336 |
|
|
|
8 |
336 |
8 |
|
х |
|
42 |
8 |
|
|
х mod |
42 |
2 |
Номер ответа.![]()
10. Определите значение целочисленных переменных а и Ь после выполнения фрагмента программы:
![]() 1686;
1686;
Ь (а div 10) mod 5;
![]()
![]() - 126, ь- 5
- 126, ь- 5
![]() - 526, ь- 5
- 526, ь- 5
З) а- 1086, ь-з
![]() - 1286, Ь- З
- 1286, Ь- З
Решение
Составим и заполним таблицу:
|
|
Команда присваивания |
Значение а |
Значение Ь |
|
а |
1686 |
1686 |
|
|
Ь |
(а div 10) mod 5 |
1686 |
з |
|
|
|
1086 |
з |
• 13.
![]()
11. х и после выполнения фрагмента программы:
![]()
у : = х mod у;
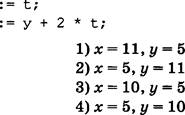
Решение
Составим и заполним таблицу:
|
Команда присваивания |
Значение х |
Значение у |
Значение t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х mod у |
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 2.
12. Определите значение целочисленных переменных х и у после выполнения фрагмента программы:
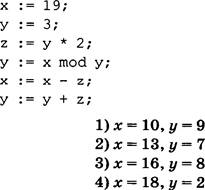
Решение
Составим и заполним таблицу:
|
Команда присваивания |
Значение х |
Значение у |
Значение z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х rnod у |
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: 2.
13.
![]()
![]()
ах- 13, у- 13, 2 - 13
![]()
Решение
Составим и заполним таблицу:
|
Команда присваивания |
Значение х |
Значение у |
Значение z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер ответа: З.
14. Определите значение целочисленных переменных а и Ь после выполнения фрагмента программы:
![]() - 2468;
- 2468;
Ь (а тод 1000) * 10; ![]() а div 1000 + Ь;
а div 1000 + Ь;
1)а - 22, Ь- 20
2) а = 4682, Ь- 4680
3) а - 8246, Ь- 246
4) а - 470, Ь = 468
Решение
Составим и заполним таблицу:
|
|
Команда присваивания |
Значение а |
Значение Ь |
|
|
2468 |
2468 |
|
|
Ь |
(а mod 1000) |
2468 |
4680 |
|
|
а div 1000 + |
4682 |
4680 |
1. Запишите значение переменной Ь после выполнения фрагмента алгоритма:
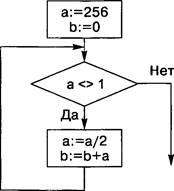
В бланк ответа впишите только число.
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
|
Значение логического выражения |
|
|
256 |
|
|
|
|
256 |
|
|
|
|
|
|
истинно (256 1) |
|
|
128 |
|
|
|
|
128 |
128 |
|
|
|
|
|
истинно (128 * 1) |
|
|
|
128 |
|
|
|
|
192 |
|
|
|
|
|
истинно (64 * 1) |
|
|
|
192 |
|
|
|
|
|
|
|
|
|
|
истинно (32 * 1) |
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
истинно (16 1) |
|
|
|
240 |
|
|
|
|
248 |
|
|
|
|
|
истинно (8 * 1) |
|
|
|
248 |
|
|
|
|
|
|
|
|
|
|
истинно (4 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (2 1) |
|
|
|
|
|
|
|
|
255 |
|
|
|
|
|
ложно (1 = 1) |
2.
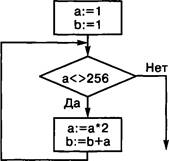
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
а |
|
Значение логического выражения |
|
1 |
1 |
|
|
|
Ь 1 |
1 |
1 |
|
|
о 256 |
|
|
истинно (1 * 256) |
|
* 2 |
2 |
1 |
|
|
а |
2 |
з |
|
|
256 |
|
|
истинно (2 * 256) |
|
* 2 |
4 |
|
|
|
|
4 |
7 |
|
|
256 |
|
|
истинно (4 256) |
|
* 2 |
8 |
7 |
|
|
|
8 |
15 |
|
|
о 256 |
|
|
истинно (8 256) |
|
* 2 |
16 |
15 |
|
|
|
16 |
31 |
|
|
256 |
|
|
истинно (16 * 256) |
|
а * 2 |
32 |
31 |
|
|
Команда |
а |
|
Значение логического выражения |
|
а |
32 |
63 |
|
|
256 |
|
|
истинно (32 256) |
|
2 |
64 |
63 |
|
|
|
|
127 |
|
|
256 |
|
|
истинно (64 * 256) |
|
2 |
128 |
127 |
|
|
|
128 |
255 |
|
|
256 |
|
|
истинно (128 * 256) |
|
а 2 |
256 |
255 |
|
|
|
256 |
511 |
|
|
256 |
|
|
ложно (256 =256) |
Ответ: 511.
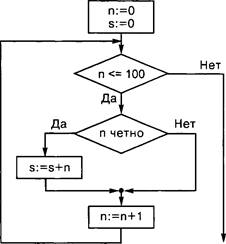
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
п |
|
Значение логического выражения |
|
п |
О |
О |
|
|
S |
О |
о |
|
|
|
|
|
истинно (О 100) |
|
п четно |
|
|
ложно (О не четно и не нечетно) |
|
|
1 |
|
|
|
100 |
|
|
истинно (1 100) |
|
п четно |
|
|
ложно (1 — нечетно) |
|
п 1 |
2 |
|
|
|
|
2 |
|
истинно (2 < 100) |
|
п четно |
|
|
истинно (2 — четно) |
|
S п |
2 |
2 |
|
|
п П 1 |
з |
2 |
|
|
|
|
|
истинно (З < 100) |
|
п четно |
|
|
ложно (З — нечетно) |
|
п |
4 |
2 |
|
|
|
|
|
истинно (4 < 100) |
|
п четно |
|
|
истинно (4 — четно) |
|
п |
4 |
6 |
|
|
п |
5 |
6 |
|
|
100 |
|
|
истинно (5 100) |
|
п четно |
|
|
ложно (5 — нечетно) |
|
п |
6 |
6 |
|
|
и т. д. |
|
|
|
2+4+6+ . . . 96 + 98 + 100 - 102 25 - 2550. Ответ: 2550.
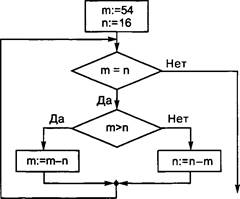
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (54 16) |
|
|
|
|
|
истинно (54 > 16) |
|
|
|
|
|
|
|
|
|
|
|
ложно (38 * 16) |
|
|
|
|
|
истинно (38 > 16) |
|
|
|
|
|
|
|
|
|
|
|
ложно (22 * 16) |
|
|
|
|
|
истинно (22 > 16) |
|
|
|
|
|
|
|
|
|
|
|
ложно (6 16) |
|
|
|
|
|
ложно (6 16) |
|
|
|
|
|
|
|
|
|
Команда |
|
п |
Значение логического выражения |
|
т |
|
|
|
ложно (б * 4) |
|
|
|
|
|
истинно (6 > 4) |
|
|
|
2 |
4 |
|
|
|
|
|
|
ложно (2 4) |
|
|
|
|
|
ложно (2 < 4) |
|
п |
п |
2 |
2 |
|
|
|
п |
|
|
истинно (2 = 2) |
Ответ: 2.
5.
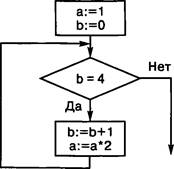
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
а |
|
Значение логического выражения |
||||
|
|
1 |
О |
|
||||
|
|
1 |
|
|
||||
|
4 |
|
|
ложно (О * 4) |
||||
|
1 |
1 |
1 |
|
||||
|
Команда |
|
|
Значение логического выражения |
|
||||
|
|
|
|
|
|
||||
|
|
|
|
ложно (1 * 4) |
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
ложно (2 * 4) |
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
ложно (3 4) |
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
истинно (4 - 4)— |
|
||||
Ответ: 16.
6.
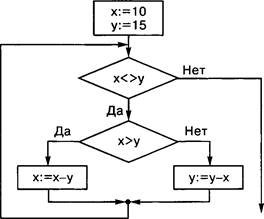
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
х |
|
Значение логического выражения |
||
|
х |
10 |
|
10 |
|
|
|
|
15 |
|
10 |
15 |
|
|
|
|
|
|
|
истинно (10 * 15) |
|
|
|
|
|
|
ложно (10 15) |
|
|
у |
х |
10 |
5 |
|
|
|
|
|
|
|
истинно (10 * 5) |
|
|
|
|
|
|
истинно (10 > 5) |
|
х |
х |
|
5 |
5 |
|
|
|
|
|
|
ложно (5 = 5) |
|
Ответ: 5.
7.
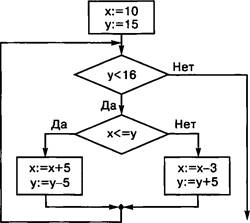
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (15 < 16) |
|
|
|
|
истинно (10 15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (10 16) |
|
|
|
|
ложно (15 > 10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (15 16) |
|
|
|
|
истинно (12 15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (10 < 16) |
|
|
|
|
ложно (17 > 10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (15 < 16) |
|
|
|
|
истинно (14 15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (10 < 16) |
|
|
|
|
ложно (19 > 10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (15 < 16) |
|
|
|
|
ложно (16 > 15) |
|
|
|
|
|
|
|
|
|
|
8. а после выполнения фрагмента алгоритма:
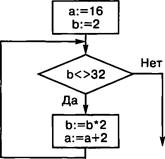
Решение
|
|
Команда |
а |
|
Значение логического выражения |
|
|
|
16 |
|
16 |
|
|
|
|
|
|
16 |
2 |
|
|
|
32 |
|
|
|
истинно (2 * 32) |
|
|
|
2 |
16 |
4 |
|
|
|
|
2 |
18 |
4 |
|
|
|
32 |
|
|
|
истинно (4 32) |
|
|
|
2 |
18 |
8 |
|
|
а |
|
2 |
20 |
8 |
|
|
|
32 |
|
|
|
истинно (8 32) |
|
|
|
2 |
20 |
16 |
|
|
|
|
2 |
22 |
16 |
|
|
|
32 |
|
|
|
истинно (16 32) |
|
|
|
2 |
22 |
32 |
|
|
а |
|
2 |
24 |
32 |
|
|
|
32 |
|
|
|
ложно (32 = 32) |
Ответ: 24.
8 ДергачеваЛ. М.
9. п после выполнения фрагмента алгоритма:
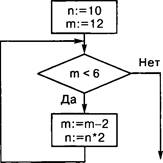
Решение
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (12 > 6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (10 > 6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (8 > 6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (6 - 6)— |
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (4 6) |
|
Ответ: 160.
10. х и у после выполнения фрагмента алгоритма:
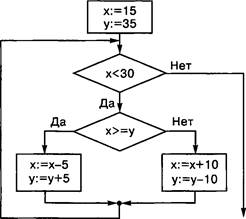
Решение
|
|
Команда |
х |
|
Значение логического выражения |
|
|
х |
15 |
|
15 |
|
|
|
|
35 |
|
15 |
35 |
|
|
|
|
|
|
|
истинно (15 < 30) |
|
|
|
|
|
|
ложно (15 35) |
|
х |
|
|
|
35 |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
истинно (25 30) |
|
|
|
|
|
|
истинно (25 = 25) |
|
х |
х |
5 |
20 |
25 |
|
|
|
|
5 |
20 |
зо |
|
|
|
|
|
|
|
истинно (20 < 30) |
|
|
|
|
|
|
ложно (20 < 30) |
|
х |
|
|
|
зо |
|
|
|
|
20 |
|
||
|
|
|
|
ложно (30 = 30) |
||
Ответ: 30, 20.
11.
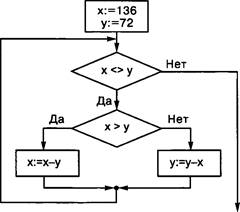
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
|
Значение логического выражения |
|
|
х 136 |
136 |
|
|
|
|
у : = 72 |
136 |
72 |
|
|
|
|
|
|
истинно (136 * 72) |
|
|
|
|
|
истинно (136 > 72) |
|
|
х |
х |
64 |
72 |
|
|
|
|
|
|
истинно (64 * 72) |
|
|
|
|
|
ложно (64 < 72) |
|
|
х |
|
8 |
|
|
|
|
|
|
истинно (64 * 8) |
|
|
|
|
|
истинно (64 > 8) |
|
х |
х |
56 |
8 |
|
|
|
|
|
|
истинно (56 * 8) |
|
|
|
|
|
истинно (56 > 8) |
|
х |
х |
48 |
8 |
|
|
|
|
|
истинно (48 * 8) |
|
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
истинно (48 > 8) |
|
|
х |
х |
40 |
8 |
|
|
|
|
|
|
истинно (40 * 8) |
|
|
|
|
|
истинно (40 > 8) |
|
х |
х |
32 |
8 |
|
|
|
|
|
|
истинно (32 * 8) |
|
|
|
|
|
истинно (32 > 8) |
|
х |
х |
24 |
8 |
|
|
|
|
|
|
истинно (24 * 8) |
|
|
|
|
|
истинно (24 > 8) |
|
х |
х |
16 |
8 |
|
|
|
|
|
|
истинно (16 * 8) |
|
|
|
|
|
истинно (16 > 8) |
|
х |
х |
8 |
8 |
|
|
|
|
|
ложно (8 = 8) |
|
12, Определите значения переменных х и у после выполнения фрагмента алгоритма:
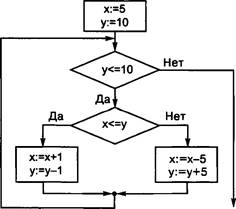
Решение
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (10 |
10) |
|
|
|
|
истинно (5 |
10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (9 |
10) |
|
|
|
|
истинно (6 |
9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (8 |
10) |
|
|
|
|
истинно (7 |
9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (7 |
10) |
|
|
|
|
ложно (8 > 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (12 10) |
|
З, 12.
13. Ь
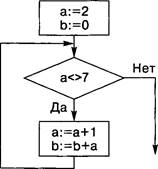
Решение
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (2 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (3$ 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (4 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (5 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (б * 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (7 = 7) |
25.
14. Ь
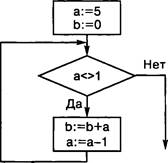
Решение
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (5 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (4 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (З |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (2 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (1 = 1) |
14.
15.
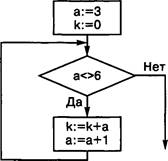
Решение
|
Команда |
а |
К |
Значение логического выражения |
|
|
|
з |
о |
|
|
|
|
З |
|
|
|
|
|
|
|
истинно (З * 6) |
|
|
К К |
а |
З |
з |
|
|
|
1 |
4 |
|
|
|
|
|
|
|
истинно (4 * 6) |
|
|
а |
4 |
7 |
|
|
а |
1 |
5 |
7 |
|
|
|
|
|
|
истинно (5 * 6) |
|
К К |
а |
5 |
12 |
|
|
|
1 |
6 |
12 |
|
|
|
|
|
ложно (6 = 6) |
|
Ответ: 12.
16. Определите значение переменной s после выполнения фрагмента алгоритма:
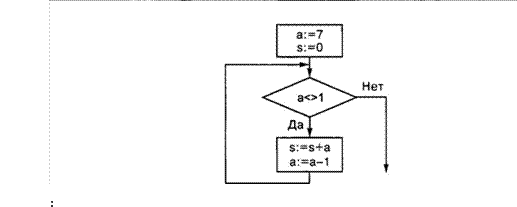
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (7 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (6 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (5 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (4 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (З * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (2 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (1 = 1) |
Ответ: 27.
17.
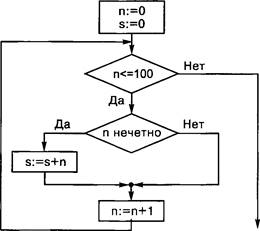
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
|
Команда |
п |
|
Значение логического выражения |
|
п |
|
О |
О |
|
|
|
|
О |
о |
|
|
|
|
|
|
истинно (О < 100) |
|
п |
нечетно |
|
|
ложно (О — четно) |
|
п |
|
1 |
|
|
|
|
|
|
|
истинно (1 100) |
|
п |
нечетно |
|
|
истинно (1 — нечетно) |
|
|
S п |
1 |
1 |
|
|
п |
П 1 |
2 |
1 |
|
|
|
|
|
|
истинно (2 < 100) |
|
п |
нечетно |
|
|
ложно (2 — четно) |
|
п |
|
з |
1 |
|
|
|
Команда |
п |
|
Значение логического выражения |
|
|
|
|
|
истинно (З 100) |
|
п |
нечетно |
|
|
истинно (З — нечетно) |
|
|
п |
з |
4 |
|
|
п |
1 |
4 |
4 |
|
|
|
100 |
|
|
истинно (4 100) |
|
п |
нечетно |
|
|
ложно (4 — четно) |
|
п |
|
5 |
4 |
|
|
|
|
|
|
истинно (5 100) |
|
п |
нечетно |
|
|
истинно (5 — нечетно) |
|
|
п |
5 |
9 |
|
|
п |
1 |
6 |
9 |
|
|
ит. д. |
|
|
|
|
Таким образом, значение переменной s равно сумме всех нечетных чисел от О до 100 включительно:
1 +3+5+ ... 95 + 97 + 99 = 100 • 2500. Ответ: 2500.
18.
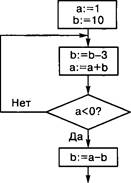
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (1 > О) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (8 > О) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (12 > О) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (13 > О) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (11 > О) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (6 > О) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (—2 < О) |
|
|
|
|
|
Ответ: 6.
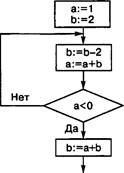
Решение
|
Команда |
а |
|
Значение логического выражения |
|
1 |
1 |
|
|
|
Ь 2 |
1 |
2 |
|
|
|
|
|
ложно (1 > О) |
|
2 |
1 |
|
|
|
ь |
1 |
|
|
|
|
|
|
ложно (1 > О) |
|
Ь Ь 2 |
1 |
-2 |
|
|
Ь |
-1 |
-2 |
|
|
|
|
|
истинно (—1 < О) |
|
|
-1 |
-3 |
|
20. Определите значение переменной Ь после выполнения фрагмента алгоритма:
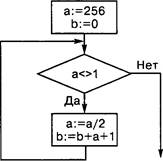
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
256 |
|
|
|
|
|
|
истинно (256 1) |
|
|
128 |
|
|
|
|
128 |
|
|
|
|
|
|
истинно (128 * 1) |
|
|
|
|
|
|
|
|
194 |
|
|
|
|
|
истинно (64 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (32 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (16 * 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (8 1) |
|
|
|
253 |
|
|
|
|
|
|
|
|
|
|
истинно (4 * 1) |
|
|
|
258 |
|
|
|
|
|
|
|
|
|
|
истинно (2 * 1) |
|
|
|
|
|
|
|
|
263 |
|
|
|
|
|
ложно (1 = 1) |
21.
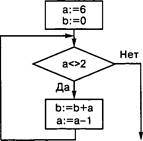
Решение
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (6 * 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (5 * 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (4 * 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (З * 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (2 = 2) |
Ответ: 18.
22.
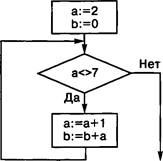
Решение
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (2 * 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (З * 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (4 * 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (5 * 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (б * 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложно (7 = 7) |
Ответ: 31.
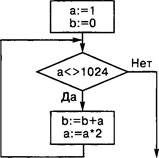
Решение
Проследим изменение значений переменных, воспользовавшись следующей таблицей:
|
Команда |
|
|
Значение логического выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
истинно (1 * 1024) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а 1024 |
|
|
|
|
|
|
|
|
истинно (2 |
1024) |
|
|
|
|
|
|
|
а <> 1024 |
|
|
истинно (4 |
1024) |
|
|
|
|
|
|
|
|
|
|
|
|
|
а о 1024 |
|
|
истинно (8 |
1024) |
|
|
|
|
|
|
|
|
|
|
|
|
|
а 1024 |
|
|
истинно (16 |
1024) |
|
|
|
|
|
|
из
![]()
|
Команда |
а |
|
Значение логического выражения |
|
|
32 |
31 |
|
|
1024 |
|
|
истинно (32 1024) |
|
|
32 |
63 |
|
|
|
64 |
63 |
|
|
1024 |
|
|
истинно (64 * 1024) |
|
|
64 |
127 |
|
|
|
128 |
127 |
|
|
1024 |
|
|
истинно (128 * 1024) |
|
|
128 |
255 |
|
|
а |
256 |
255 |
|
|
1024 |
|
|
истинно (256 * 1024) |
|
|
256 |
511 |
|
|
|
512 |
511 |
|
|
1024 |
|
|
истинно (512 * 1024) |
|
|
512 |
1023 |
|
|
а |
1024 |
1023 |
|
|
1024 |
|
|
ложно (1024 = 1024) |
ответ: 1023.
24. Значения двух массивов „4[1..100] и В[1..100] задаются с помощью следующего фрагмента программы:
for п : = 1 to 100 do
![]()
for п : = 1 to 100 do
![]()
Сколько элементов массива В будут иметь положительные значения?
2) 50
3) 90
4) 100
![]()
Решение
Положительные значения будут иметь 90 элементов массива А. Элементы же массива В получаются путем умножения элементов массива А на п — порядковый номер элемента. Таким образом, 90 элементов массива В будут иметь положительные значения. Номер ответа: З.
25. Значения двумерного массива задаются с помощью вложенного оператора цикла в представленном фрагменте программы: for п : = 1 to 5 do for К: = 1 to 5 do
![]()
Чему будет равно значение В [2,4]?
![]()
Решение
Значение любого элемента двумерного массива В равно сумме номеров столбца и строки данного элемента. Следовательно, значение элемента В [2,4] = 2 + 4 = 6. Номер ответа: 4.
26. Дан фрагмент:
for п : = 1 to 6 до for т : = 1 to 5 do begin
С [п, т] :=С [п, т] + (2*n-m) ; end;
Чему будет равно значение С [4,3], если перед этими командами значение С [4,3] = 10?
2) 10
4) 25
Решение
Значение любого элемента двумерного массива равно его предыдущему значению, увеличенному на значение выражения 2 • п — т. Таким образом, значение элемента С [4,3] = 10 + (2 • 4 — З) = 15. Номер ответа: З.
27. Значения элементов двух массивов А и В размером 1х 100 задаются с помощью следующего фрагмента программы:
![]()
for i:=1 to 100
do ![]() 50 i; for i:=1 to 100 do
50 i; for i:=1 to 100 do
![]()
Сколько элементов массива В будут иметь отрицательные значения?
2) 10
3) 50
4) 100
Решение
Отрицательные значения будут иметь 50 элементов массива А:
![]() 50- 51; А [511=-1; А [521=50- 52; А
[511=-2 ит. д.;
50- 51; А [511=-1; А [521=50- 52; А
[511=-2 ит. д.;
А 50 - 100; А [1001=-50.
Таким образом, только один элемент массива В будет иметь отрицательное значение В [100] -50 + 49; вдоој -1. Номер ответа: 1.
28. Значения элементов двумерного массива А размером 5х 5 задаются с помощью вложенного цикла в представленном фрагменте программы: for to 5 do for ј :=1 to 5 do begin
![]()
Сколько элементов массива будут иметь значения больше 10?
3) 10
Решение
Значение любого элемента двумерного массива А равно произведению номеров столбца и строки данного элемента. Таким образом, будут иметь значения больше 10 следующие восемь элементов массива:
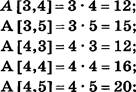

29. Значения элементов двумерного массива А размером 5х 5 задаются с помощью вложенного цикла в представленном фрагменте программы:
![]()
end;
Сколько элементов массива будут иметь значения больше 5?
2) 20
3) 10
Решение
Значение любого элемента двумерного массива А равно сумме номеров столбца и строки данного элемента. Таким образом, будут иметь значения больше 5 следующие элементы массива:
А [1,5] = 1 + 5=6• А [2,4] =2 + 4=6;
![]() А [2,5] =2
А [2,5] =2
З
А [5,4] = 5 + 4=9;
А [5,5] = 5 + 5 = 10.
Таким образом, 15 элементов массива будут иметь значения больше 5.
Номер ответа.![]()
![]()
30. Дан фрагмент программы:
for п : — to 5 do for т:=1 to 5 do
![]() (т
(т ![]() п) ;
п) ;
Сколько элементов массива С будут равны 1?
![]()
Решение
Значение любого элемента двумерного массива С равно значению выражения (т — п) • (т — п). Таким образом, будут равны 1 следующие элементы массива:
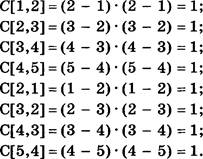
Таким образом, 8 элементов массива
будут равны 1. Номер ответа.![]()
31.
В программе описан одномерный целочисленный массив с индексами от
О до 10. В приведенном ниже фрагменте программы массив сначала заполняется, а
потом изменяется: for ![]() to 10 do
to 10 do
for i:=1 to 10 do
![]()
Как изменяются элементы этого массива?
1) все элементы, кроме последнего, сдвигаются на 1 элемент вправо
2) все элементы, кроме первого, сдвигаются на 1 элемент влево
З) все элементы окажутся равны 1
4) все элементы окажутся равны своим индексам Решение
Значения элементов массива А равны их индексам, увеличенным на 1. Поэтому элементы массива А примут значения от 1 до 11. Далее элементы массива изменяются следующим образом:
![]()
![]() [0] ФА [11= 1;
[0] ФА [11= 1;
А А [1] ЭА [21= 1;
А = А [9] ЭА [10] = 1.
Таким образом, все элементы массива А окажутся равны 1. Номер ответа: З.
32. В программе описан одномерный целочисленный массив с
индексами от О до 10. В приведенном ниже фрагменте программы массив сначала
заполняется, а потом изменяется: for ![]() to 10 do
to 10 do
![]() downto 0 do А [10-м ;
downto 0 do А [10-м ;
Чему будут равны элементы этого массива?
1) 10 9 8 76 5 4 3 2 1 0
2) 11 1098 76 54 3 2 1
3) 11 1098 76 78 9 10 11
Решение
Значения элементов массива А равны их индексам, увеличенным на 1. Поэтому элементы массива А примут значения от 1 до 11.
Далее элементы массива изменяются следующим образом:
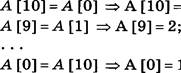 [0] ЭА [101= 1;
[0] ЭА [101= 1;
Таким образом, элементы массива А будут равны:
1 2 3 4 56 5 4 3 2 1. Номер ответа: 4.
33. В программе описан одномерный целочисленный массив с
индексами от О до 10. В приведенном ниже фрагменте программы массив сначала
заполняется, а потом изменяется: for ![]() to 10 do
to 10 do
Чему будут равны элементы этого массива?
1) 10 9 8 76 5 4 3 2 1 0
2) 11 1098 76 54 3 2 1
3) 11 109 8 76 78 9 10 11
4) 10 98 7 6 56 789 10
![]()
Решение
Значения элементов массива А равны их индексам, увеличенным на 1. Поэтому элементы массива А примут значения от 1 до 11. Далее элементы массива изменяются следующим образом:
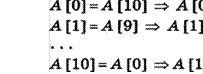 11.
11.
Таким образом, элементы массива А будут равны:
11 10 9 8 76 78 9 10 11. Номер ответа: З.
![]() 34. В программе описан одномерный целочисленный массив с
индексами от О до 10. В приведенном ниже фрагменте программы массив сначала
заполняется, а потом изменяется: for to 10 do
34. В программе описан одномерный целочисленный массив с
индексами от О до 10. В приведенном ниже фрагменте программы массив сначала
заполняется, а потом изменяется: for to 10 do
i - 1 ; for i:=1 to 10 do
![]()
Как изменяются элементы этого массива?
1) все элементы, кроме последнего, окажутся равны между собой
2) все элементы окажутся равны своим индексам
З) все элементы, кроме последнего, сдвигаются на один элемент вправо
4) все элементы, кроме последнего, уменьшаются на единицу Решение
Значения элементов массива А равны их индексам, уменьшенным на 1. Поэтому элементы массива А примут значения от —1 до 9. Далее элементы массива изменяются следующим образом:
![]()
А [1] = А [2] ЭА [11=1;
![]() 10.
10.
Таким образом, все элементы массива А окажутся равны своим индексам.
Номер ответа: 2.
![]() 35. В программе
описан одномерный целочисленный массив с индексами от О до 10. В приведенном
ниже фрагменте программы массив сначала заполняется, а потом изменяется: for to
10 до
35. В программе
описан одномерный целочисленный массив с индексами от О до 10. В приведенном
ниже фрагменте программы массив сначала заполняется, а потом изменяется: for to
10 до
-i;
![]()
![]()
Чему будут равны элементы этого массива?
1) 10 9 8 76 5 4 3 2 1 0
2) 11 109 8 7 6 54 3 2 1
3) 1098 76 5 6 78 9 10
4) 11 1098 76 789 10 11
Решение
Значения элементов массива А равны их индексам. Поэтому элементы массива А примут значения от О до 10. Далее элементы массива изменяются следующим образом:
А [О] = А [10] ЭА [0] = 10;
![]()
![]() [0] = А 10.
[0] = А 10.
Таким образом, элементы массива А будут равны:
1098 7 6 5 6 78 9 10. Номер ответа: З.
36. В программе описан одномерный целочисленный массив с
индексами от О до 10. В приведенном ниже фрагменте программы массив сначала
заполняется, а потом изменяется: for ![]() to 10 do A[i] :=i;
for to 10 do begin
to 10 do A[i] :=i;
for to 10 do begin
end;
Чему будут равны элементы этого массива?
2) 0 1 2 3 4 5 6 78 9 10
3) 109 8 7 6 5 6 7 8 9 10
4) 0 1 2 3 4 5 4 3 2 1 0
Решение
Значения элементов массива А равны их индексам. Поэтому элементы массива А примут значения от О до 10. Далее элементы массива изменяются следующим образом:
А [10], А [0] ![]() и А
и А![]()
![]()
Таким образом, элементы массива А будут равны:
0 1 2 3 4 5 4 3 2 1 0.
Номер ответа: 4.
37. Элементы двумерного массива А размером 9 х 9 задаются с помощью следующего фрагмента программы: for п: = 1 Ео 9 do for К: = 1 to 9 do
А [п, К] :=n+k+1;
Сколько элементов массива А будут принимать четные значения?
1) 36
2) 40
3) 41
Решение
Массив А содержит 81 элемент. При этом четные значения будут принимать элементы, сумма номера строки и номера столбца которых нечетна, так как затем данная сумма увеличивается на 1 и становится четной. Искомых элементов — на один меньше, чем элементов, значения которых нечетны. Таким образом, четные значения будут принимать 40 элементов массива А. Номер ответа: 2.
![]()
for п : =1 to 100 do в [101-п] П [п] ;
Какой элемент массива В будет наименьшим?
1) B[11
2) В[50]
3) B[511 4) В[100]
Решение
Значение любого элемента массива А равно разности индекса данного элемента и числа 50. Поэтому элементы массива А будут принимать значения от —49 до 50.
Затем вычисляются значения элементов массива В:
В [100] = А [1] • А [1] В [100] = -49 • (-49) В [100] = 2401; В [99] = А [2] • А [2] В [99] = -48 • (-48) В [99] = 2304;
![]() [50] • А [50] — В [511 = 0 . О эв
[50] • А [50] — В [511 = 0 . О эв ![]() ит. д.
ит. д.
Таким образом, все элементы массива В, кроме элемента В [51], примут положительные значения. Значение же элемента В [51] станет равно О, оно и будет наименьшим. Номер ответа: З.
39. В программе описан одномерный целочисленный массив с индексами от О до 10 и целочисленные переменные К, i. В приведенном ниже фрагменте программы массив сначала заполняется, а потом изменяется:
for to 10 do A [i] :=i; for 1 ' : =10 downto 0 do begin
![]()
end;
Чему будут равны элементы этого массива?
2) 0 1 2 34 5 6 789 10
3) 1098 76 5 6 789 10
4) 0 1 2 34 54 3 2 1 0
Решение
![]() [01;
[01;
А [10] = А [01 и А [О] = А [10].
Таким образом, в итоге элементы массива А не изменят своих значений и будут равны:
0 1 2 34 5 6 78 9 10. Номер ответа: 2.
40. Элементы двумерного массива А размером 4 х 4 первоначально были равны О. Затем они изменяются с помощью следующего фрагмента программы:
for п: = 1 to 4 do for К:=п to 4 do
![]()
Сколько элементов массива А будут равны 1? 3) 10
4) 16
Решение
Значения элементов массива А, расположенные на главной диагонали и под ней, будут равны 1. Их количество равно: 4 + 6 = 10. Номер ответа: З.
41.
Дан фрагмент программы, обрабатывающий массив А из 10 элементов:
п ![]() for i:=1 to п do А [1] -i;
for i:=1 to п do А [1] -i;
Ј 1; for i:=1 to п- 1 do
-if A[i] < А [1+1] then ј![]()
Чему будет равно значение переменной .i после выполнения этого алгоритма?
3) 10
Решение
Таким образом, значение переменной ј увеличится на 9 и станет равным 10.
Номер ответа: З.
42. Значения элементов двумерного массива ![]() , 1 . .1001 задаются с помощью
следующего фрагмента программы: for to 100 do for К:=1 to 100 do .if -i К then
, 1 . .1001 задаются с помощью
следующего фрагмента программы: for to 100 do for К:=1 to 100 do .if -i К then
![]() 1
1
Чему равна сумма элементов массива после выполнения этого фрагмента программы?
2) -9800
3) -9900
4) -10000
![]()
Решение
Массив А содержит 10 ООО элементов. При этом 100 элементов будут расположены на главной диагонали и будут иметь значения, равные 1. Оставшиеся 9900 элементов примут значения, равные —1.
Таким образом, для нахождения суммы элементов массива нужно вычислить значение выражения:
100 1 + 9900 = -9800. Номер ответа: 2.
![]() 43. Значения
элементов двумерного массива .4[1..100 , 1 . .100] задаются с помощью
следующего фрагмента программы: for to 100 do ior К: = 1 to 100 do if
43. Значения
элементов двумерного массива .4[1..100 , 1 . .100] задаются с помощью
следующего фрагмента программы: for to 100 do ior К: = 1 to 100 do if
1
-1;
Чему равна сумма элементов массива после выполнения этого фрагмента программы?
2) 100
3) -100
4) —200
Решение
Массив А содержит 10 ООО элементов. При этом 100 элементов расположены на главной диагонали и будут иметь значения, равные —1. Кроме того, такие же значения будут иметь элементы, находящиеся над главной диагональю. Оставшиеся 4950 элементов примут значения, равные 1.
Таким образом, для нахождения суммы элементов массива нужно вычислить значение выражения:
100 • (-1)+ 4950 • + 4950 • 1 = -100. Номер ответа: З.
44. Значения элементов двумерного массива АД.. 100,1 . .100] задаются с помощью следующего фрагмента программы: for i :=1 to 100 do for К: = 1 to 100 do if -i > К then
![]()
Чему равна сумма элементов массива после выполнения этого фрагмента программы?
![]()
1) 5000
3) -5000 4) -5050
Решение
Массив А содержит 10 ООО элементов. При этом 4950 элементов, расположенных под главной диагональю, равны номеру своей строки, а оставшиеся 5050 элементов равны номеру столбца, умноженному на —1. При этом сумма элементов, расположенных под и над главной диагональю массива, равна О. Для нахождения же искомой суммы необходимо вычислить:
—1 + + + (—4 ) + + (—98) + (_99) + (—100) =
= 50 • (-101) - -5050. Номер ответа: 4.
45, В программе описан одномерный целочисленный массив с индексами от О до 10 и целочисленная переменная i. В приведенном ниже фрагменте программы массив сначала заполняется, а потом изменяется:
for to 10 do A [i] :=i; for to 9 do begin
end;
Чему будут равны элементы этого массива?
1) 100 1 2 3 4 56 789
2) 1 2 3 4 5 6 7 8 9 10 10
Решение
Значения элементов массива А равны их индексам. Поэтому элементы массива А примут значения от О до 10. Далее значения элементов массива изменяются следующим образом:
![]()
А [9] = А [10].
Таким образом, элементы массива А будут равны:
1 2 3 4 5 6 7 8 9 10 10. Номер ответа: 2.
46. В программе описан одномерный целочисленный массив с индексами от О до 10 и целочисленные переменные К, i. В приведен256
![]()
ном ниже фрагменте программы массив сначала заполняется, а потом изменяется:
for i:=O to 10 do A[i)![]()

Чему будут равны элементы этого массива?
2) 102 3 4 5 6 789 10 10
3) 1 2 3 4 5 6 78 9 10 10
Решение
Значения элементов массива А равны их индексам. Поэтому элементы массива А примут значения от О до 10. Далее значения элементов массива изменяются следующим образом:
![]()
А = А [10].
Затем выполняется присваивание А [О] = 10. Таким образом, элементы массива А будут равны:
102 3 4 5 6 789 10 10. Номер ответа: 2.
47. Дан фрагмент программы, обрабатывающей двумерный массив А размера п х п.
К 1;
for 
end
Представим массив в виде квадратной таблицы, в которой для элемента массива величина i является номером строки, а величина .i — номером столбца, в котором расположен элемент. Тогда данный алгоритм меняет местами:
1) два столбца в таблице
2) две строки в таблице
З) элементы главной диагонали и К-й строки таблицы
4) элементы главной диагонали и К-го столбца таблицы
![]()
Решение
В результате выполнения данного фрагмента программы первый элемент главной диагонали меняется местами с первым элементом первой строки; второй элемент главной диагонали — со вторым элементом первой строки и т. д. до п элементов с номером. Таким образом, в фрагменте программы меняются местами элементы главной диагонали и К-й строки. Номер ответа: З.
48. Значения элементов двумерного массива АД..10,1 . .10] задаются с помощью следующего фрагмента программы: for i:=1 to 10 do for К:=1 to 10 do
-if i > К then
![]() 1 о ;
1 о ;
Чему равна сумма элементов массива после выполнения этого фрагмента программы?
1) 45
2) 50
3) 90
4) 100
Решение
Массив А содержит 100 элементов. При этом 10 элементов будут расположены на главной диагонали и будут иметь значения, равные нулю. Кроме того, такие же значения будут иметь элементы, находящиеся над главной диагональю. Оставшиеся же 45 элементов примут значения, равные 1.
Таким образом, для нахождении суммы элементов массива нужно вычислить значение выражения:
![]()
Номер ответа: 1.
9 ДергачеваЛ. М.
Технология кодирования, создания и обработки текстовой, графической, числовой и мультимедийной информации.
Технология создания, хранения, поиска и сортировки информации в базах данных.
Файловая система
1. Определите информационный объем текста:
Бамбарбия! Кергуду !
1) 38 бит
2) 144 бит З) 152 бит
4) 19 бит
|
Дано: К = 19 символов i = 8 бит |
Решение Воспользуемся формулой:
|
|
Найти: I— ? |
Номер ответа: З. |
2. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 480 бит. Какова длина сообщения в символах?
2) 60
3) 120
4 ) 48 О
![]()
|
Дано: i1 = 8 бит i2 = 16 бит I2 — I1 = 480 бит |
Решение Воспользуемся формулой:
Значит, 12 -11 Следовательно, 8 • К = 480 К = 60 (символов). |
|
Найти:
|
Номер ответа: 2. |
З. В таблице ниже представлена часть кодовой таблицы ASCII:
|
Символ |
1 |
5 |
А |
в |
Q |
а |
|
|
Десятичный код |
49 |
53 |
65 |
66 |
81 |
97 |
98 |
|
Шестнадцатеричный код |
|
|
|
|
|
|
|
Каков шестнадцатеричный код символа q?
16
2) 8316
3) А116
4) ВЗ16
Решение
В этом задании рассмотрен фрагмент стандартной части таблицы ASCII, содержащей цифры, заглавные и строчные буквы английского алфавита. Следует вспомнить один из принципов организации таблицы ASCII: в ней соблюдается лексикографический порядок в расположении букв. Значит, количество букв, находящихся между символами А и Q, такое же, как и между а и q. Шестнадцатеричный код буквы А на 10 больше шестнадцатеричного кода буквы Q. Следовательно, шестнадцатеричный код буквы q будет на 10 больше, чем шестнадцатеричный код буквы а, т. е. 61 + 10 = 71. Номер ответа: 1.
![]()
4. Считая, что каждый символ кодируется одним байтом, определите, чему равен информационный объем следующего высказывания Жан-Жака Руссо:
Тысячи путей ведут х заблужденпо, к истине — только ортн .
1) 92 бит
2) 220 бит З) 456 бит
4) 512 бит
|
Дано: К = 57 символов i = 8 бит |
Решение Воспользуемся формулой:
|
|
Найти:
|
Номер ответа: З. |
5. Считая, что каждый символ кодируется одним байтом, определите, чему равен информационный объем следующего высказывания Алексея Толстого:
не оиибается тот, кто ничего не делает, хотя это и есть его основная оиибха .
1) 512 бит
2) 608 бит
З) 8 Кбайт
4) 123 байт
|
Дано: К = 76 символов i = 8 бит |
Решение Воспользуемся формулой:
|
|
Найти:
|
Номер ответа: 2. |
6. Считая, что каждый символ кодируется одним байтом, определите, чему равен информационный объем следующего высказывания Рене Декарта:
Я ослю, следовательно, существую .
1) 28 бит З) 32 Кбайт
2) 272 бит 4) 34 бит
|
Дано: К = 34 символа i = 8 бит |
Решение: Воспользуемся формулой: —1=34 -8=272 (бит). |
|
Найти:
|
Номер ответа: 2. |
7. В кодировке Unicode на каждый символ отводится два байта. Определите информационный объем слова из двадцати четырех символов в этой кодировке.
1) 384 бит 2) 192 бит З) 256 бит
|
Дано: К — 24 символа i — 16 бит |
Решение Воспользуемся формулой:
|
|
Найти:
|
Номер ответа: 1. |
8. Считая, что каждый символ кодируется 16 битами, оцените информационный объем следующей пушкинской фразы в кодировке Unicode:
Привычка свьше нам дана: Замена счастиш она .
1)44 бит
2)704 бит З) 44 байт
4) 704 байт
|
Дано: К = 44 символа i = 16 бит |
Решение Воспользуемся формулой:
|
|
Найти:
|
Номер ответа: 2. |
9. Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения:
Певец Давид был ростом мал, Но повалил же Голиафа !
1) 400 бит
2) 50 бит
З) 400 байт
4) 5 байт
|
Дано: к- 50 8 бит |
Решение Воспользуемся формулой:
|
|
Найти:
|
Номер ответа: 1. |
10. Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения:
Мой дядя са.»љх честных правил, Когда не в шутку занемог , он уважать себя заставил И лучше выдумать не мог .
1)
2) 848 бит
З) 106 Кбайт
4) 848 Кбайт
|
Дано: К = 106 символов i = 8 бит |
Решение Воспользуемся формулой
|
|
Найти:
|
Номер ответа: 2. |
11. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 8-битном коде, в 16-битную кодировку Unicode. При этом информационное сообщение увеличилось на 2048 байт. Каков был информационный объем сообщения до перекодировки?
1) 1024 байт
2) 2048 бит З) 2 Кбайт 4) 2 Мбайт
|
Дано: i1 = 8 бит 16 бит 12-11- = 2048 байт = = 16384 бита |
Решение Воспользуемся формулой: I = k . i,
Значит:
Следовательно: 8 • К = 16384 К = 2048 (символов) = К • i1 = 2048 • 8 = 16384 (бит) = 2 (Кбайт). |
|
Найти:
|
Номер ответа: З. |
12. Считая, что каждый символ кодируется 16 битами, оцените информационный объем следующей фразы в кодировке Unicode:
В шести литрах 6000 миллилитров .
1) 1024 байт
2) 1024 бит З) 512 байт
|
Дано: К = 32 символа i = 16 бит |
Решение: Воспользуемся формулой:
|
|
Найти:
|
Номер ответа: 4. |
13, Считая, что каждый символ кодируется 16 битами, оцените информационный объем следующего предложения:
Блажен, кто верует, тепло ему на свете !
1) 78 бит
2) 80 байт З) 312 бит 4) 624 бит
|
Дано: к=39 i=16 |
Решение Воспользуемся формулой:
|
|
Найти: I— ? |
Номер ответа: 4. |
14. Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения:
Белеет Парус Одинокий В Тумане Моря Голубом !
1) 352 бит З) 352 байт
2)
|
Дано:
|
Решение Воспользуемся формулой:
|
|
Найти: I— ? |
Номер ответа: 1. |
15. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 800 бит. Какова длина сообщения в символах?
1) 50 3) 200
2) 100 4) 800
|
дано:
I1 — I2 = 800 бит |
Решение Воспользуемся формулой: 1
Значит,
Следовательно: 8 • К = 800 К = 100 (символов). |
|
Найти:
|
Номер ответа: 2. |
16. В таблице ниже представлена часть кодовой таблицы ASCII:
|
Символ |
1 |
5 |
|
|
|
|
к |
|
Десятичный код |
49 |
53 |
|
|
|
106 |
107 |
|
Шестнадцатеричный код |
31 |
35 |
|
|
50 |
|
|
Каков шестнадцатеричный код символа р?
16
2) 8516
3) 6F16
Решение
17. В таблице ниже представлена часть кодовой таблицы:
|
Символ |
С |
т |
|
я |
с |
|
|
|
Десятичный код |
145 |
146 |
147 |
159 |
225 |
226 |
227 |
|
Шестнадцатеричный код |
|
|
|
|
|
|
ЕЗ |
Каков шестнадцатеричный код символа я? 1) 2А116
2) DF16
3) EF16
4) 18016
Решение
В задании рассмотрен фрагмент расширенной таблицы ASCII, содержащей цифры, заглавные и строчные буквы английского и русского алфавитов. Следует вспомнить один из принципов организации данной таблицы: в ней соблюдается лексикографический по-
рядок в расположении букв. Значит, количество букв, находящихся между символами У и Я, такое же, как и между у и я. Шестнадцатеричный код буквы Я на 12 больше шестнадцатеричного кода буквы У. Следовательно, шестнадцатеричный код буквы я будет на 12 больше, чем шестнадцатеричный код буквы у, т. е. ЕЗ + 12 = EF. Номер ответа: З.
1)белый
2)зеленый З) красный
4) синий
Решение
Совмещение трех компонент Ж}В-модели дает нейтральный, серый цвет, который при большой интенсивности стремится к белому. В предложенном задании для каждого цвета задана максимальная интенсивность, значит, цвет фона страницы будет белым. Номер ответа: 1.
2. Для хранения растрового изображения размером 32 х 32 пикселя отвели 512 байт памяти. Каково максимально возможное число цветов в палитре изображения?
1) 256
|
Дано: т = 32 п: 32 I= 512 байт |
Решение Общее количество пикселей изображения равно:
|
|
Найти:
|
Номер ответа: З. |
З. Для хранения растрового изображения размером 64 х 64 пикселя отвели 512 байт памяти. Каково максимально возможное число цветов в палитре изображения?
3) 256
4)
|
Дано: т = 64 п = 64 I= 512 байт |
Решение Общее количество пикселей изображения равно: Q=m.n I = 512 байт = 2 9 байт = 2 12 бит, тогда: N=I/Q 2 12 /2 12= 2 0 = 1 (бит). Воспользовавшись формулой = N, получим: 2 1 = 2 (цвета). |
|
Найти:
|
Номер ответа: 2. |
4. Для хранения растрового изображения размером 128 х 128 пикселей отвели 4 килобайта памяти. Каково максимально возможное число цветов в палитре изображения?
3) 16
|
Дано: т = 128 п = 128 I = 4 Кбайт |
Решение Общее количество
пикселей изображения равно: I = 4 Кбайт = 2 2 Кбайт = 2 12 байт = 2 15 бит,
тогда: = |
|
Найти:
|
Номер ответа: 4. |
5.
|
Дано: ля = 1024 ль = 32 |
Решение Воспользуемся формулои 2 Получим: 2 1 - 1024, следовательно, i1 = 10 (бит); 2 2 = 32, следовательно, i2 = 5 (бит). Таким образом, информационный объем файла до преобразования равен I1 = К • i1, а информационный объем файла после преобразования равен I2 = К • i2. Следовательно,
|
|
Найти: |
Номер ответа: 2. |
6. Монитор позволяет получать на экране 2 24 цветов. Какой объем памяти в байтах занимает 1 пиксель?
|
Дано: |
Решение Получить 2 24 цветов можно в режиме True Color. При этом информация о цвете каждого пикселя растрового изображения хранится в виде набора его МЭВ-составляющих. Каждая из этих трех составляющих может принимать одно из значений в диапазоне [О, 255]. Следовательно, для представления каждого из трех цветов необходимо i бит, причем 2 11 =N, где N — количество значений заданного диапазона. Тогда 2' = 256. Значит, i1 = 8 (бит) = 1 (байт) — для одной составляющей. Тогда для трех составляющих необходимо в три раза больше памяти, т. е. З байта. |
|
Найти:
|
Номер ответа: 2. |
7. Разрешение экрана монитора — 1024 х 768 точек, глубина цвета — 16 бит. Каков необходимый объем видеопамяти для данного графического режима?
1) 6 Мбайт 2) 256 байт З) 4 Кбайт
4) 1,5 Мбайт
|
Дано: т = 1024 п = 768 i = 16 бит |
Решение Общее количество пикселей изображения равно:
18 • = З • 2 22 (бит) = З • 2 19 (байт) = З • 2 9 (Кбайт) = = 1,5 (Мбайт). |
|
Найти:
|
Номер ответа: 4. |
8.
2) 64 3) 32 4) 128
|
Дано: т = 1024 17=512 I = 256 Кбайт |
Решение Общее количество пикселей изображения равно:
I = 256 Кбайт = 2 8 Кбайт = 2 21 бит. Тогда N=I/Q 2 21 /2 19 — 2 2 = 4 (бит). Воспользовавшись формулой 2' = N, получим 2 4 = 16 (цветов). |
|
Найти: N—? |
Номер ответа: 1. |
9. Для хранения растрового изображения размером 128 х 128 пикселей используется 8 Кбайт памяти. Каково максимально возможное количество цветов в палитре данного изображения?
3) 32
|
Дано: т = 128 п = 128 I = 8 Кбайт |
Решение Общее
количество пикселей изображения равно: |
|
Найти:
|
Номер ответа: 2. |
10.
|
Дано: лк = 512 |
Решение: Воспользуемся формулой: 2' = N. Получим: 2' 1 — 512, следовательно, il = 9 (бит); 22 8, следовательно, i2 = З (бит). Таким образом, информационный объем файла до преобразования равен I1 = К • i1, а информационный объем файла после преобразования равен
Следовательно:
|
|
Найти:
|
Номер ответа: З. |
11. После преобразования растрового 256-цветного графического файла в черно-белый формат (2 цвета) его размер уменьшился на 70 байт. Каков был размер исходного файла?
1) 70 байт
2) 640 бит
3) 80 бит
4) 560 бит
|
Дано: N1- 256
|
Решение Воспользуемся формулой: 2 l = N. Получим: 2' 1 = 256, следовательно, i1 = 8 (бит);
2!2 = 2, следовательно, i2 —— 1 (бит). Таким образом, информационный объем файла до преобразования равен I1 = • i1, а информационный объем файла после преобразования равен 2— Следовательно: I1 — = К • i1 — К i2 = 70 (байт) = 560 (бит). Тогда: К • 8 — К • 1 = 560, откуда К = 80. Отсюда I1 = К • i1 = 80 • 8 = 640 (бит). |
|
Найти:
|
Номер ответа: 2. |
12.
|
Дано: N1 = 64 |
Решение Воспользуемся формулой: 2! = N. Получим: 1 = 64, следовательно, i1 = 6 (бит); 2 2 = 8, следовательно, i2 = З (бит). Таким образом, информационный объем файла до преобразования равен I1 = К • i1, а информационный объем файла после преобразования равен = К • i2. Следовательно: 11/12 = К • i1/k • i2 = i1/i2 = 6/3 = 2 (раза). |
|
Найти: |
Номер ответа: 2. |
13. Сколько памяти нужно для хранения 64-цветного растрового графического изображения размером 32 на 128 точек?
1) 32 Кбайт
2) 64 байт
3) З Кбайт
4) 4096 байт
|
Дано: т = 32 п = 128 = 64 |
Решение: Общее количество пикселей изображения равно:
Воспользуемся формулой: 2' = N. Получим: 2' = 64. Значит, i = 6 (бит).
|
|
Найти: I— ? |
Номер ответа: З. |
1) белый
2) зеленый З) красный
4) синий
Решение
В предложенном задании для зеленого цвета задана максимальная интенсивность, тогда как остальные цвета взяты с нулевой инТеНСИВНОСТЬЮ. Значит, цвет фона страницы будет зеленым. Номер ответа: 2.
15. Для кодирования цвета фона
Интернет-страницы используется атрибут bgc010r= ” #ХХХХХХ” , где в кавычках
задаются шестнадцатеричные значения интенсивности цветовых компонент в
24-битной Ж}В-модели. Какой цвет фона будет у страницы, заданной тегом <body![]()
1) белый
2) зеленый
З) красный
4) синий
Решение
В предложенном задании для синего цвета задана максимальная интенсивность, тогда как остальные цвета взяты с нулевой интенсивностью. Значит, цвет страницы будет синим. Номер ответа: 4.
16. Для кодирования цвета фона
Интернет-страницы используется атрибут bgcolor=” #ХХХХХХ” , где в кавычках
задаются шестнадцатеричные значения интенсивности цветовых компонент в
24-битной Ж}В-модели. К какому цвету будет близок цвет фона страницы, заданной
тегом <body bgc010r=”![]()
1) белый
2) серый
З) желтый
4) фиолетовый
Решение
17. Для кодирования цвета фона
Интернет-страницы используется атрибут bgc010r= ” #ХХХХХХ” , где в кавычках
задаются шестнадцатеричные значения интенсивности цветовых компонент в
24-битной Ж}В-модели. К какому цвету будет близок цвет фона страницы, заданной
тегом <body bgcolor=”![]()
1) белый
2) серый
З) желтый
4) фиолетовый
Решение
В предложенном задании для красного и синего цветов задана средняя интенсивность, тогда как зеленый цвет взят с небольшой интенсивностью. Значит, цвет фона страницы будет фиолетовым. Номер ответа: 4.
18. Для кодирования цвета фона Интернет-страницы
используется атрибут bgc010r=” #ХХХХХХ ” , где в кавычках задаются
шестнадцатеричные значения интенсивности цветовых компонент в 24-битной
Ж}В-модели. К какому цвету будет близок цвет фона страницы, заданной тегом
<body![]()
10 ДергачеваЛ. М.
1) белый
2) серый
З) желтый
4) фиолетовый
Решение
В предложенном задании для красного и зеленого цветов задана средняя интенсивность, тогда как синий цвет взят с нулевой интенсивностью. Значит, цвет фона страницы будет желтым. Номер ответа: З.
19. Для кодирования цвета фона Интернет-страницы используется атрибут bgc010r=” #ХХХХХХ” , где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной Ж}В-модели. К какому цвету будет близок цвет фона страницы, заданной тегом <body bgcolor="#40FF40">?
1) темно-фиолетовый
2) светло-зеленый
З) желтый
4) светло-желтый
Решение
20.
Для кодирования цвета фона Интернет-страницы используется атрибут
bgcolor=” #ХХХХХХ” , где в кавычках задаются шестнадцатеричные значения
интенсивности цветовых компонент в 24-битной Ж}В-модели. К какому цвету будет
близок цвет фона страницы, заданной тегом <body bgcolor=”![]()
1) темно-фиолетовый
2) светло-зеленый
З) желтый
4) светло-желтый
Решение
В предложенном задании для красного и зеленого цветов задана максимальная интенсивность, тогда как синий цвет взят с небольшой интенсивностью. Значит, будет получен светлый оттенок, а цвет фона страницы будет светло-желтым. Номер ответа: 4.
21.
Для кодирования
цвета фона Интернет-страницы используется атрибут bgc010r= ” #ХХХХХХ” , где в
кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в
24-битной Ж}В-модели. К какому цвету будет близок цвет фона страницы, заданной
тегом <body bgcolor=”![]()
1) темно-фиолетовый
2) светло-зеленый
З) желтый
4) светло-желтый
Решение
В предложенном задании для красного и синего цветов задана небольшая интенсивность, тогда как зеленый цвет взят с нулевой интенсивностью. Значит, будет получен темный оттенок, а цвет фона страницы будет темно-фиолетовым. Номер ответа: 1.
22. Какова ширина (в пикселях) прямоугольного 64-цветного неупакованного растрового изображения, занимающего на диске 1,5 Мбайт, если его высота вдвое меньше ширины?
1) 256
2) 512
3)
4) 2048
|
Дано: I = 1,5 Мбайт ЛТ 64 т/п = 1/2 |
Решение Воспользуемся формулои 2 — Получим: = 64, значит, i = 6 (бит). I = 1,5 Мбайт = З • 2 22 бит. т • n=I/i т п = З • 2 22 /6= 2 21 (пикселей). Поскольку т/п = 1/2, то п = 2 11 = 2048 (пикселей). |
|
Найти:
|
Номер ответа: 4. |
23. Какова ширина (в пикселях) прямоугольного 16-цветного неупакованного растрового изображения, занимающего на диске 1 Мбайт, если его высота вдвое больше ширины?
1) 256 3) 1024
2) 512 4) 2048
|
Дано: 1 = 1 Мбайт N=16
|
Решение: Воспользуемся формулои 2 Получим: 2' = 16, значит, т п = I/i т • п = 2 23 /4 = 2 21 (пикселей). Поскольку т / п = 2, то п = 2 10 = 1024 (пикселя). |
|
Найти:
|
Номер ответа: З. |
24.
Для кодирования цвета фона Интернет-страницы используется атрибут
bgco 10r= ” #ХХХХХХ ” , где в кавычках задаются шестнадцатеричные значения
интенсивности цветовых компонент в 24-битной RGB-rvro№JIPI. К какому цвету
будет близок цвет фона страницы, заданной тегом <body bgc010r=”![]()
1) черный
2) темно-синий
З) темно-зеленый 4) темно-красный
Решение
25.
Для кодирования цвета фона Интернет-страницы используется атрибут
bgco 10r= ” #ХХХХХХ ” , где в кавычках задаются шестнадцатеричные значения
интенсивности цветовых компонент в 24-битной Ж}В-модели. К какому цвету будет
близок цвет фона страницы, заданной тегом <body bgc010r=”![]()
1) красный
2) желтый
З) фиолетовый
4) голубой
Решение
В предложенном задании для зеленого и синего цветов задана максимальная интенсивность, тогда как красный цвет взят с нулевой интенсивностью. Значит, цвет фона страницы будет голубым. Номер ответа: 4.
26.
Для кодирования цвета фона Интернет-страницы используется атрибут
bgcolor= ” #ХХХХХХ ” , где в кавычках задаются шестнадцатеричные значения
интенсивности цветовых компонент в 24-битной Ж}В-модели. К какому цвету будет
близок цвет фона страницы, заданной тегом <body bgcolor=”![]()
1) желтый
2) розовый
З) светло-зеленый
4) светло-синий
Решение
В предложенном задании для красного цвета задана максимальная интенсивность, тогда как остальные цвета взяты с небольшой интенсивностью. Значит, цвет фона страницы будет иметь светлый оттенок, в данном случае розовый. Номер ответа: 2.
27.
Для кодирования цвета фона Интернет-страницы используется атрибут
bgcolor= ” #ХХХХХХ ” , где в кавычках задаются шестнадцатеричные значения
интенсивности цветовых компонент в 24-битной Ж}В-модели. К какому цвету будет
близок цвет фона страницы, заданной тегом <body![]()
1) желтый
2)
З) светло-зеленый
4) светло-синий
Решение
В предложенном задании для зеленого цвета задана максимальная интенсивность, тогда как остальные цвета взяты с небольшой интенсивностью. Значит, цвет фона страницы будет иметь светлый оттенок, в данном случае светло-зеленый. Номер ответа: З.
Математическая обработка статистических данных
1. В электронной таблице значение формулы =СУММ(В1:В2) равно
5. Чему равно значение ячейки ВЗ, если значение формулы  равно 3?
равно 3?
Решение
Представленные в условии задачи формулы можно записать следующим образом: В1 + В2 — 5, (В1 + В2 + ВЗ)/З = З.
11 ДергачеваЛ. М.
Подставив значение В1 + В2 — 5 во вторую формулу, получим:
(5 + взуз = з. Значит, вз = 4. Номер ответа: 4.
2. В ячейке В1 записана формула =2*$А1. Какой вид приобретет эта формула после того, как ячейку В1 скопируют в ячейку (2?
1) -2*$В1
2) -2*$А2
![]()
4) -3*$В2Н
Решение
При копировании формулы =2*$А1 изменяется только имя строки, увеличиваясь на 1. Таким образом, формула приобретет вид -2*$А2.
Номер ответа: 2.
З. В ячейке С2 записана формула =$E$3+D2. Какой вид приобретет эта формула после того, как ячейку С2 скопируют в ячейку В1 ?
1) =$Е$З+С1
2) =$D$3+D2
3)
4) =$F$4+D2
Решение
При копировании формулы =$E$3+D2 изменяется только второе слагаемое, имя столбца и строки в котором уменьшаются на 1. Таким образом, формула приобретет вид =$Е$З+С1. Номер ответа: 1.
4. Дан фрагмент электронной таблицы:
|
|
А |
в |
С |
D |
|
1 |
5 |
2 |
4 |
|
|
2 |
10 |
1 |
6 |
|
В ячейку D2 введена формула ![]() +С1. В
результате в ячейке
+С1. В
результате в ячейке
D2 появится значение:
3) 16 4 ) 24
Решение
Подставив значения ячеек А2, В1, С1 в формулу =А2*В1+С1, получим: —10 * 2 + 4. Значит, D2 = 24. Номер ответа: 4.
5. В ячейке А1 электронной таблицы записана формула =D1-$D2. Какой вид приобретет эта формула после того, как ячейку А 1 скопируют в ячейку В1?
1) -Е1-$Е2
2) -E1-$D2
3) -E2-$D2
4) =D1-$E2
Решение
При копировании формулы —D1-$D2 изменяется только первое слагаемое, имя столбца в котором увеличивается на 1. Таким образом, формула приобретет вид =E1-$D2. Номер ответа: 2.
|
|
А |
в |
с |
|
|
1 |
1 |
2 |
З |
|
|
2 |
4 |
5 |
6 |
|
|
з |
7 |
8 |
9 |
|
В ячейку D1 введена формула =$А$1*В1+С2, а затем скопирована в ячейку D2. Какое значение в результате появится в ячейке D2?
2) 14 4) 24
Решение
При копировании формулы —$А$ 1*В1+С2 в ячейку D2 получим формулу =$А$1*В2+СЗ. Подставив значения ячеек А1, В2, СЗ в формулу =$А$1*В2+СЗ, получим: —1 * 5 + 9, значит, D2 — 14. Номер ответа: 2.
7. В ячейке В2 записана формула =$D$2+E2. Какой вид будет иметь эта формула, если ячейку В2 скопировать в ячейку А 1?
1) -$D$2+E1
2) -$D$2+C2
3) =$D$2+D2
4) -$D$2+D1
Решение
При копировании формулы =$D$2+E2 изменяется только второе слагаемое, имя столбца и строки в котором уменьшаются на 1. Таким образом, формула приобретет вид —$D$2+D1. Номер ответа: 4.
8. В ячейке СЗ электронной таблицы записана формула =$А$ 1+В1. Какой вид будет иметь эта формула, если ячейку СЗ скопировать в ячейку ВЗ?
1) =$А$1+А1
2) -$в$1+В3
3) -$А$1+ВЗ
Решение
При копировании формулы =$А$1+В1 изменяется только второе слагаемое, имя столбца в котором уменьшается на 1. Таким образом, формула приобретет вид —$А$1+А1. Номер ответа: 1.
9. При работе с электронной таблицей в ячейке ЕЗ записана формула —В2+$СЗ. Какой вид приобретет эта формула после того, как ячейку ЕЗ скопируют в ячейку 02?
1) -А1+$СЗ
2) =А1+$С2
3) =E2+$D2
4) -D2+$E2
Решение
10. В ячейке электронной таблицы В4 записана формула =С2+$А$2. Какой вид приобретет эта формула, если ячейку В4 скопировать в ячейку С5?
1) =D2+$B$3
2) -С5+$А$2
3) -D3+$A$2
4) =СЗ+$А$З
Решение
При копировании формулы =С2+$А$2 изменяется только первое слагаемое, имя столбца и строки в котором увеличиваются на 1. Таким образом, формула приобретет вид =D3+$A$2. Номер ответа: З.
11. В ячейке электронной таблицы А 1 записана формула =$D1+D$2. Какой вид приобретет эта формула, если ячейку А1 скопировать в ячейку ВЗ?
1) =D1+$E2
2) -D3+$F2
3) =E2+D$2 4) =$D3+E$2
Решение
При копировании формулы =$D1+D$2 изменяется имя строки в первом слагаемом, увеличиваясь на 2, и имя столбца во втором слагаемом, увеличиваясь на 1. Таким образом, формула приобретет вид -$D3+E$2.
Номер ответа: 4.
12. В электронной таблице значение формулы =СРЗНАЧ(А6:С6) равно —2. Чему равно значение формулы =CYMM(A6:D6), если значение ячейки D6 равно 5?
![]()
Решение
(Аб + Вб + Сб)/3 = -2, тогда
Аб + Вб + Сб + - -2 • З + 5.
Значит, Аб + Вб + Сб + D6 = -1. Номер ответа: 2.
13.
В электронной таблице значение формулы —СРЗНАЧ(А6:С6) равно 0,1.
Чему равно значение формулы ![]() если значение ячейки D6 равно —1?
если значение ячейки D6 равно —1?
Решение
Представленные в условии задачи формулы можно записать следующим образом:
(Аб + Вб + Сб)/З — 0,1, тогда
Аб + Вб + Сб + D6 - З +![]()
Значит, Аб + Вб + Сб + D6 = —0,7. Номер ответа: 1.
14.
В электронной таблице значение формулы =СРЗНАЧ(В5:Е5) равно 100.
Чему равно значение формулы ![]() если значение ячейки F5 равно 10?
если значение ячейки F5 равно 10?
1) 90
2) 110
3) 310
4) 41 О
Решение
Представленные в условии задачи формулы можно записать следующим образом:
(В5 + С5 + D5 + Е5)/4 = 100, тогда
В5 + C5 + + Е5 + F5 = 100 • 4 + 10.
Значит, + С5 + D5 + Е5 + F5 = 410. Номер ответа: 4.
15.
![]()
Решение
Представленные в условии задачи формулы можно записать следующим образом:
(Аб + Вб + Сб)/3 = 2, тогда
Аб + Вб + + - 2 . З + (-5).
Значит, Аб + Вб + Сб + 06 - 1.
Номер ответа: 1.
16.
В электронной таблице значение формулы =СУММ(СЗ:ЕЗ) равно 15.
Чему равно значение формулы ![]() если значение ячейки F3 равно 5?
если значение ячейки F3 равно 5?
1) 20
2) 10
Решение
Представленные в условии задачи формулы можно записать следующим образом:
СЗ + 03 + ЕЗ - 15, тогда
(СЗ + D3 + ЕЗ + F3)/4 - (15 + 5)/4. Значит, (СЗ + D3 + ЕЗ + F3)/4 - 5.
З.
17. В динамической (электронной) таблице приведены значения пробега автомашин (в км) и общего расхода дизельного топлива (в литрах) в четырех автохозяйствах с 12 по 15 июля:
|
|
12 июля |
13 июля |
14 июля |
15 июля |
За четыре дня |
|||||
|
Название автохозяйства |
|
|
|
|
|
|
|
|
|
|
|
Автоколонна М 11 |
9989 |
2134 |
9789 |
2056 |
9234 |
2198 |
9878 |
2031 |
38890 |
8419 |
|
Грузовое такси |
490 |
101 |
987 |
215 |
487 |
112 |
978 |
203 |
2942 |
631 |
|
Автобаза 6 |
1076 |
147 |
2111 |
297 |
4021 |
587 |
1032 |
143 |
8240 |
1174 |
|
Трансавтопарк |
998 |
151 |
2054 |
299 |
3989 |
601 |
1023 |
149 |
8064 |
1200 |
В каком из хозяйств средний расход топлива на 100 км пути за эти четыре дня наименьший?
1) Автоколонна № 11
2)
Решение
Воспользуемся данными столбцов «Пробег за четыре дня» и «Расход за четыре дня» .
Расход топлива автохозяйства «Автоколонна 11» составляет 8419 л за 38 890 км. Вычислим средний расход топлива на 100 км пути, составив пропорцию и найдя необходимое значение:
38 890 8419;
100 ![]() тогда х 21,648 (л).
тогда х 21,648 (л).
Расход топлива автохозяйства «Грузовое такси» составляет 631 л за 2942 км. Вычислим средний расход топлива на 100 км пути, составив пропорцию и найдя необходимое значение:
2942 631;
100 х; тогда х 21,448 (л).
Расход топлива автохозяйства «Автобаза 6» составляет 1174 л за 8240 км. Вычислим средний расход топлива на 100 км пути, составив пропорцию и найдя необходимое значение:
8240 1174;
100 х; тогда х * 14,248 (л).
Расход топлива автохозяйства «Трансавтопарк» составляет 1200 л за 8064 км. Вычислим средний расход топлива на 100 км пути, составив пропорцию и найдя необходимое значение:
8064 1200;
100 х; тогда х 14,881 (л).
Сравнив полученные результаты, получим, что наименьший средний расход топлива на 100 км пути за четыре дня — у автохозяйства «Автобаза 6» .
Номер ответа: З.
18.
В электронной таблице значение формулы —СРЗНАЧ(А1:С1) равно 5.
Чему равно значение ячейки Т, если значение формулы  равно 7?
равно 7?
Представленные в условии задачи формулы можно записать следующим образом:
(А 1 + В1 + С1)/З = 5, тогда
А1 +В1 + СЛ +D1 = 5 . З + 01 = 7.
Значит, D1 -8.
Номер ответа: 2.
19.
В электронной таблице значение формулы ![]() равно 4. Чему равно
значение ячейки А 1, если значение формулы
равно 4. Чему равно
значение ячейки А 1, если значение формулы  равно 9?
равно 9?
Решение
Представленные в условии задачи формулы можно записать следующим образом:
(В1 + С1 + D1)/3 = 4, тогда
![]()
Значит, А 1 — -3.
1.
20. В электронной таблице значение формулы =СРЗНАЧ(А1:В4) равно З. Чему равно значение ячейки М, если значение формулы —СУММ(А1:ВЗ) равно 30, а значение ячейки В4 равно 5?
Решение
Представленные в условии задачи формулы можно записать следующим образом:
(А 1 + А? + АЗ + А4 + В1 + В? + ВЗ + В4)/8 = З. Тогда:
А1 + А2 + АЗ + В1 + В2 + ВЗ = 30,
А1 + А2 + АЗ + В1 + В2 + ВЗ - 8 . З - В4 - М.
Значит, А4 = -30 + 24 - 5 - -11.
Номер ответа: 1.
21.
![]()
|
|
|
в |
с |
|
|
|
|
1 |
1 |
З |
4 |
8 |
2 |
|
|
2 |
4 |
—5 |
-2 |
1 |
5 |
5 |
|
з |
5 |
5 |
5 |
5 |
5 |
5 |
|
4 |
2 |
з |
1 |
4 |
4 |
2 |
2) 29
Решение
Подставив значения необходимых ячеек в формулу ![]() получим:
- (3 - 5 + 5 + З +4- 2 + 5 + 1) + + 5 • 4 — 5. Следовательно, значение,
вычисленное по указанной формуле, равно 29.
получим:
- (3 - 5 + 5 + З +4- 2 + 5 + 1) + + 5 • 4 — 5. Следовательно, значение,
вычисленное по указанной формуле, равно 29.
Номер ответа: 2.
22. На рисунке приведен фрагмент электронной таблицы. Определите, чему будет равно значение, вычисленное по формуле
![]()
|
|
|
в |
с |
D |
Е |
|
|
1 |
1 |
З |
4 |
8 |
2 |
|
|
2 |
4 |
-5 |
-2 |
1 |
5 |
5 |
|
|
5 |
5 |
5 |
5 |
5 |
5 |
|
4 |
2 |
з |
1 |
4 |
4 |
2 |
З) 45
4) 55
Решение
Подставив значения необходимых ячеек в формулу ![]() получим: =
(1 + 4 + З - 5 + 4 - 2) 2 х х 5 — 5. Следовательно, значение, вычисленное по
указанной формуле, равно 45.
получим: =
(1 + 4 + З - 5 + 4 - 2) 2 х х 5 — 5. Следовательно, значение, вычисленное по
указанной формуле, равно 45.
Номер ответа: З.
23. В электронной таблице значение формулы =СРЗНАЧ(А4:С4) равно 5. Чему равно значение формулы =CYMM(A4:D4), если значение ячейки D4 равно 6?
3) 16
Решение
Представленные в условии задачи формулы можно записать следующим образом:
![]()
Значит, А4 + В4 + C4 + 04 - 21. Номер ответа: 4.
24. В электронной таблице значение
формулы ![]() равно 5. Чему равно значение формулы
=СРЗНАЧ(АЗ:С4), если значение формулы =CYMM(D3:D4) равно 4?
равно 5. Чему равно значение формулы
=СРЗНАЧ(АЗ:С4), если значение формулы =CYMM(D3:D4) равно 4?
![]()
Решение
Представленные в условии задачи формулы можно записать следующим образом:
(АЗ + А4 + ВЗ + В4 + СЗ + С4 + D3 + D4)/8 = 5, (АЗ + А4 + ВЗ + В4 + СЗ + С4 + 4)/8 = 5. Тогда: АЗ + М + вз + ва + сз + = 5 - 8 - 4, АЗ + А4 + ВЗ + В4 + СЗ + С4 = 36.
Значит, (АЗ + А4 + ВЗ + ва + СЗ + С4)/6 = 6. 4.
Использование инструментов решения статистических и расчетно-графических задач
1. На диаграмме показано количество призеров олимпиады по информатике (И), математике (М) и физике (Ф) в трех городах России.
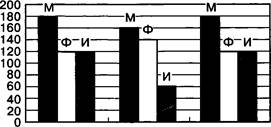
Екатеринбург Томск Новосибирск
Какая из диаграмм правильно отражает соотношение общего числа призеров по каждому предмету для всех городов вместе?
Решение
Вычислим количество призеров по каждому предмету и общее число призеров:
о информатика — ЗОО призеров; е
математика — 520 призеров; ![]() физика — 380 призеров.
физика — 380 призеров.
Общее число призеров — 1200.
Сопоставив полученные значения, получим, что количество призеров по математике меньше половины общего числа призеров, что отражено на диаграммах 1 и 4. Количество же призеров по физике больше, чем по информатике, что соответствует диаграмме 1. Номер ответа: 1.
2, Дан фрагмент электронной таблицы:
|
|
|
в |
с |
|
|
1 |
|
з |
4 |
|
|
2 |
-С1-В1 |
-В1-А2*2 |
-C1/2 |
-В1+В2 |
После выполнения вычислений была построена диаграмма по значениям диапазона ячеек A2:D2. Укажите получившуюся диаграмму.
Решение
|
|
А |
в |
с |
|
|
1 |
|
з |
4 |
|
|
2 |
1 |
1 |
2 |
4 |
Диаграмма построена по значениям диапазона ячеек A2:D2, что соответствует четвертому варианту. Номер ответа: 4.
З. Дан фрагмент электронной таблицы:
|
|
|
в |
|
1 |
|
1 |
|
2 |
|
2 |
|
з |
-В2-1 |
|
|
4 |
|
|
После выполнения вычислений была построена диаграмма по значениям диапазона ячеек А1:А4. Укажите получившуюся диаграмму.
Решение
После выполнения вычислений фрагмент электронной таблицы примет вид:
|
|
А |
в |
|
1 |
2 |
1 |
|
2 |
4 |
2 |
|
з |
1 |
|
|
4 |
1 |
|
Диаграмма построена по значениям диапазона ячеек А1:А4, что соответствует второму варианту. Номер ответа: 2.
1) 2)
![]()
![]() 40 зо 20
40 зо 20
10
Есть 4 утверждения:
А) Все учителя I категории могут являться учителями математики.
Б) Все учителя I категории могут являться учителями физики. В) Все учителя информатики могут иметь высшую категорию.
Г) Все учителя математики могут иметь П категорию.
Какое из этих утверждений следует из анализа обеих представленных диаграмм?
Решение
Согласно диаграмме 2, в телеконференции приняли участие 50 учителей математики, 25 учителей физики и 25 учителей информатики. Сопоставив имеющиеся значения, получим, что все учителя I категории могут являться учителями математики. Таким образом, из анализа обеих диаграмм следует первое утверждение.
Номер ответа: 1.
|
|
Население, млн чел. |
|
|
1970 год |
1989 год |
|
|
Австралия и Океания |
19 |
26 |
|
Африка |
361 |
628 |
|
Европа |
642 |
701 |
|
Южная Америка |
190 |
291 |
|
Северная и Центральная Америка |
320 |
422 |
|
Азия |
2161 |
3133 |
Диаграмма 1:
Население, млн чел.
![]() 3500
3500
3000
2500
2000 1500 1000
500
1970 год 1989 год
• Австралия и Океания • Африка
![]() Европа •
Южная Америка
Европа •
Южная Америка
![]() Северная и Центральная Америка а
Азия
Северная и Центральная Америка а
Азия
Диаграмма 2:
Население, млн чел.
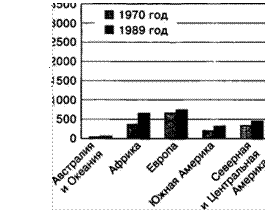
1) Обе диаграммы верно отражают данные, представленные в таблице.
2) Ни одна из диаграмм не соответствует данным, представленным в таблице.
З) Данным, представленным в таблице, соответствует только диаграмма 1.
4) Данным, представленным в таблице, соответствует только диаграмма 2.
Решение
Сопоставив значения, имеющиеся во фрагменте электронной таблицы, получим, что обе диаграммы верно отражают данные, представленные в ней.
Номер ответа: 1.
6. Имеется фрагмент электронной таблицы:
|
|
Название пролива |
Длина (км) |
Глубина(м) |
|
1 |
Босфор |
зо |
20 |
|
2 |
Магелланов |
575 |
29 |
|
З |
Ормузский |
195 |
27 |
|
4 |
Гудзонов |
806 |
141 |
|
5 |
Гибралтарский |
59 |
53 |
|
6 |
Ла-Манш |
578 |
23 |
|
7 |
Баб-эль-Мандебский |
109 |
31 |
|
8 |
Дарданеллы |
120 |
29 |
|
9 |
Берингов |
96 |
36 |
По данным этой таблицы были построены диаграммы:
Диаграмма 1
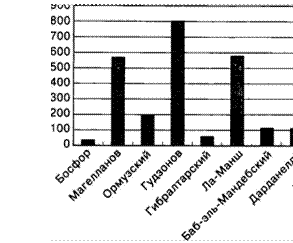
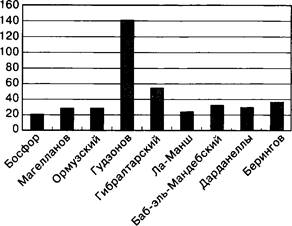
Какое из следующих утверждений истинно?
1) Обе диаграммы верно отражают данные, представленные в таблице.
2) Ни одна из диаграмм не соответствует данным, представленным в таблице.
З) Диаграмма 1 отражает глубину проливов.
4) Диаграмма 2 отражает длину проливов.
Решение
Сопоставив значения, имеющиеся во фрагменте электронной таблицы, получим, что обе диаграммы верно отражают данные, представленные в ней. Номер ответа: 1.
7. Дан фрагмент электронной таблицы:
|
|
А |
в |
|
1 |
=В2+2 |
5 |
|
2 |
=В4-1 |
|
|
3 |
|
|
|
4 |
=А2+2 |
2 |
После выполнения вычислений по значениям диапазона ячеек А1:А4 была построена диаграмма. Укажите получившуюся диаграмму.
1) 2) 3) 4)

Решение
|
|
А |
в |
|
1 |
2 |
5 |
|
2 |
1 |
|
|
з |
2 |
|
|
4 |
з |
2 |
Диаграмма построена по значениям диапазона ячеек А1:А4, что соответствует первому варианту. Номер ответа: 1.
8. В соревнованиях по зимним видам спорта принимают участие лыжники (Л), конькобежцы (К) и хоккеисты (Х). Спортсмены имеют разный уровень мастерства: каждый имеет либо III, либо П, либо I разряд, либо является мастером спорта (М). На диаграмме 1 отражено количество спортсменов с различным уровнем спортивного мастерства, а на диаграмме 2 — распределение спортсменов по видам спорта.
1) 2)
![]()
![]() 40 зо 20
40 зо 20
10
Есть 4 утверждения:
А) Все спортсмены, имеющие I разряд, могут являться конькобежцами.
Б) Все лыжники могут быть мастерами спорта.
В) Все хоккеисты могут иметь П разряд.
Г) Все спортсмены, имеющие разряд, могут являться хоккеистами.
![]()
Решение
Согласно диаграмме 2, в соревнованиях приняли участие 50 хоккеистов, 25 лыжников и 25 конькобежцев. Сопоставив имеющиеся значения, получим, что все спортсмены, имеющие I разряд, могут являться хоккеистами. Таким образом, из анализа обеих диаграмм следует четвертое утверждение. Номер ответа: 4.
9. Дан фрагмент электронной таблицы (в режиме отображения формул):

После выполнения вычисления была построена диаграмма по значениям диапазона А 1:01. Укажите полученную диаграмму:
1 ) 2) 3) 4)

Решение
После выполнения вычислений фрагмент электронной таблицы примет вид:
|
|
|
в |
с |
|
|
1 |
1 |
1 |
1 |
2 |
|
2 |
1 |
|
|
|
Диаграмма построена по значениям диапазона ячеек A1:D1, что
соответствует первому варианту. Номер ответа: 1.
10. Дан фрагмент электронной таблицы (в режиме отображения формул):
|
|
|
|
|
|
—А1*2 <'2+В1-2 |
—(B1+D2)/2 2 |
|
|
1) 2) 3) 4)

Решение
После выполнения вычислений фрагмент электронной таблицы примет вид:
|
|
|
в |
с |
D |
|
1 |
2 |
4 |
5 |
з |
|
2 |
|
|
з |
2 |
Диаграмма построена по значениям диапазона ячеек A1:D1, что соответствует третьему варианту. Номер ответа: З.
11. Дан фрагмент электронной таблицы (в режиме отображения формул):
|
|
|
В |
с |
|
|
1 :-С2-В1 -В2-С2 -В1+С2 |
- (С1-с2) |
|||
|
з 2 |
||||
После выполнения вычислений была построена диаграмма по значениям диапазона A1:D1. Укажите полученную диаграмму:
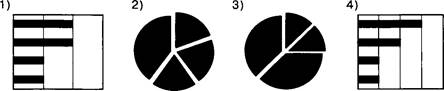
Решение
|
|
|
в |
с |
|
|
1 |
1 |
1 |
з |
з |
|
2 |
|
з |
2 |
|
Диаграмма построена по значениям диапазона ячеек A1:D1, что соответствует третьему варианту. Номер ответа: З.
12. На диаграмме показаны объемы выпуска продукции трех видов (А, Б и В) за каждый месяц первого квартала:
![]() 200
200
180
160
140
120
100
80
60
40
20
Какая из диаграмм правильно отражает соотношение объемов выпуска этих видов продукции за весь квартал?
![]() 1 ) 2) 3) 4)
1 ) 2) 3) 4)
 в
в
Решение
Согласно диаграмме 1, за все месяцы первого квартала объемы
выпуска продукции таковы:
А = 60 + 160 + 180 - 400; Б = 160 + 120 + 120 - 400; в 40 + 40 + 120 = 200.
Сопоставив имеющиеся значения, получим, что правильно отраэкает соотношение объемов выпуска продукции за весь квартал четвертая диаграмма.
Номер ответа: 4.
|
|
|
в |
с |
|
|
1 |
|
=С1-А1 |
-А1*2 |
|
|
2 |
|
4 |
2 |
|
После выполнения вычислений по значениям диапазона ячеек A1:D1 была построена диаграмма. Укажите получившуюся диаграмму.
1 ) 2) 3) 4)

Решение
После выполнения вычислений фрагмент электронной таблицы примет вид:
|
|
|
в |
с |
|
|
1 |
2 |
2 |
4 |
8 |
|
2 |
|
4 |
2 |
|
12 ДергачеваЛ. М.
Диаграмма построена по значениям диапазона ячеек A1:D1, что соответствует четвертому варианту. Номер ответа: 4.
14. Дан фрагмент электронной таблицы (в режиме отображения формул):
|
|
|
в |
|
D |
|
1 |
=В2+С2 |
-С1+В2 |
-А1-С2 |
-В1-С1 |
|
2 |
|
1 |
з |
|
После выполнения вычислений по значениям диапазона ячеек A1:D1 была построена диаграмма. Укажите получившуюся диаграмму.

Решение
После выполнения вычислений фрагмент электронной таблицы примет вид:
|
|
|
в |
с |
|
|
1 |
4 |
2 |
1 |
1 |
|
2 |
|
1 |
з |
|
Диаграмма построена по значениям диапазона ячеек A1:D1, что соответствует второму варианту. Номер ответа: 2.
15. Дан фрагмент электронной таблицы (в режиме отображения формул):
|
|
|
в |
с |
|
|
1 |
|
з |
4 |
|
|
2 |
-С1-В1 |
|
-С1/2 |
=В1+В2 |
После выполнения вычислений по значениям диапазона ячеек A2:D2 была построена диаграмма. Укажите получившуюся диаграмму.
1) 2) 3) 4)

Решение
После выполнения вычислений фрагмент электронной таблицы примет вид:
|
|
А |
в |
с |
|
|
1 |
|
З |
4 |
|
|
2 |
1 |
1 |
2 |
4 |
Номер ответа: 1.
16. На диаграмме представлено количество участников тестирования в разных регионах России:
![]() 500
500
зоо
200
100
Башкирия Чувашия Удмуртия
Какая из диаграмм правильно отражает соотношение общего количества участников тестирования по регионам?
1)2)3) 4)

зоо
![]()
Решение
Согласно диаграмме 1, общее количество участников тестирования по регионам таково:
, Башкирия — 200 + 100 + 200 = 500; ![]() Чувашия — 200 + 200 + 200 = 600;
Чувашия — 200 + 200 + 200 = 600;
, Удмуртия — 400 + ЗОО + 200 = 900.
Сопоставив имеющиеся значения с предложенными диаграммами, получим, что правильно отражает соотношение общего количества участников тестирования по регионам третья диаграмма. Номер ответа: З.
17. На диаграмме представлено количество участников тестирования в разных регионах России:
![]() 500 400
500 400
зоо
200
100
0
Башкирия Чувашия Удмуртия
Какая из диаграмм правильно отражает соотношение количества участников тестирования по химии в регионах?
1)2)3) 4)

Решение
Согласно диаграмме 1, соотношение количества участников тестирования по химии в регионах таково:
![]() Башкирия — 200;
Башкирия — 200;
![]() Чувашия — 200; е
Удмуртия — 200.
Чувашия — 200; е
Удмуртия — 200.
Сопоставив имеющиеся значения с предложенными диаграммами, получим, что правильно отражает соотношение количества участников тестирования по химии в регионах четвертая диаграмма. Номер ответа: 4.
![]()
18. На диаграмме представлено количество участников тестирования в разных регионах России:
![]() 500 400
500 400
зоо
200
100
Башкирия Чувашия Удмуртия
Какая из диаграмм правильно отражает соотношение количества участников тестирования по истории в регионах?
1)2)3) 4)

Решение
Согласно диаграмме 1, соотношение количества участников тестирования по истории в регионах таково:
![]() Башкирия — 100;
Башкирия — 100; ![]() Чувашия — 200;
Чувашия — 200;
![]() Удмуртия — ЗОО.
Удмуртия — ЗОО.
Сопоставив имеющиеся значения с предложенными диаграммами, получим, что правильно отражает соотношение количества участников тестирования по истории в регионах вторая диаграмма. Номер ответа: 2.
19. На диаграмме представлено количество участников тестирования в разных регионах России:
![]() 500 400
500 400
зоо
200
100
Башкирия Чувашия Удмуртия
![]()
Какая из диаграмм правильно отражает соотношение количества участников тестирования по биологии в регионах?
1)2)3) 4)

Решение
Согласно диаграмме 1, соотношение количества участников тестирования по биологии в регионах таково:
![]() Башкирия — 200;
Башкирия — 200;
![]() Чувашия — 200;
Чувашия — 200;
![]() Удмуртия
— 400.
Удмуртия
— 400.
Сопоставив имеющиеся значения с предложенными диаграммами, получим, что правильно отражает соотношение количества участников тестирования по биологии в регионах первая диаграмма. Номер ответа: 1.
20. Ученики четырех 10-х классов ходят на элективные курсы, причем каждый ученик выбрал только один курс. На диаграмме 1 показано количество учеников в классах, а на диаграмме 2 — сколько человек занимается каждым элективным курсом,
Диаграмма 1

![]() Диаграмма
2 35
Диаграмма
2 35
зо 25
20
15
10
5
Физика Математика Информатика История Химия
зоз
![]()
Какое из следующих утверждений следует из анализа обеих диаграмм?
1) Все ученики 10А и 10Б классов могли выбрать элективные курсы либо по химии, либо по истории.
2) Все ученики 10Г класса могли выбрать элективный курс по физике.
З) Никто из учеников 10А и 10Б классов не выбрал элективный курс по физике.
4) Все ученики 10Б класса могли выбрать элективный курс по информатике.
Решение
Используя данные из диаграммы 2, вычислим общее количество учеников, учитывая, что каждый ученик выбрал только один элективный курс:
30 + 15 + 10 + 30 + 15 — 100 (учеников).
Таким образом, согласно диаграмме 1, количество учеников в 10Г и 10В классах равно 25, в 10А классе — более 25, а в 10Б классе — менее 25.
Сопоставив полученные значения с имеющимися высказываниями и с данными из диаграммы 2, получим, что все ученики 10Г класса могли выбрать элективный курс по физике. Значит, верным является второй вариант ответа. Номер ответа: 2.
21. Девочки 5-х—б-х классов занимаются в трех кружках: вязания, вышивания и макраме, причем каждая девочка ходит только в один кружок. На диаграмме 1 показано количество девочек в классах, а на диаграмме 2 — сколько девочек занимается в каждом кружке.
диаграмма 1 Диаграмма 2

Вышивание Вязание Макраме
Какое из следующих утверждений следует из анализа обеих диаграмм?
![]()
1) В кружок вязания ходит больше девочек из 5А класса, чем из 5Б.
2) На кружке вышивания девочек 6Б класса может не быть.
З) На кружок вышивания ходит больше девочек из 6А класса, чем из 6Б.
4) Кружок макраме может состоять только из девочек 5А класса.
Решение
Используя данные из диаграммы 2, вычислим общее количество девочек, учитывая, что каждая из них выбрала только один кружок:
20 + 12 + 4 = 36 (девочек).
Таким образом, согласно диаграмме 1, количество девочек в классах 5Б и 6А одинаково, количество девочек в 5А классе равно их числу в классах 5Б и 6А, а в 6Б классе девочек столько же, сколько в трех остальных классах вместе взятых.
Сопоставив полученные значения с имеющимися высказываниями и данными из диаграммы 2, получим, что кружок макраме может состоять только из девочек 5А класса. Значит, верным является четвертый вариант ответа. Номер ответа: 4.
22. В магазине продаются мячи четырех цветов (синие, зеленые, красные и желтые) и трех размеров (большие, средние и маленькие). На диаграмме 1 показано количество мячей разного размера, а на диаграмме 2 — распределение мячей по цветам.
Диаграмма 1 Диаграмма 2
![]()
![]() 45
45
40 35 зо 25
20
15
10
5
И Большие Средние
О Маленькие Синий Зеленый Красный Желтый
Какое из следующих утверждений следует из анализа обеих диаграмм?
1) Все маленькие мячи могут быть синими или желтыми.
2) Среди больших мячей найдется хотя бы один красный.
З) Среди маленьких мячей найдется хотя бы один зеленый или красный.
4) Все красные мячи могут быть среднего размера.
![]()
Решение
Используя данные из диаграммы 2, вычислим общее количество мячей:
30 + 40 + 35 + 15 = 120 (мячей).
Таким образом, согласно диаграмме 1, количество больших и средних мячей одинаково и равно 30, а количество маленьких мячей равно числу больших и средних мячей вместе взятых (т. е. 60 мячей).
Сопоставив полученные значения с имеющимися высказываниями и с данными из диаграмм, получим, что среди маленьких мячей найдется хотя бы один зеленый или красный. Значит, верным является третий вариант ответа. Номер ответа: З.
23. В магазине продаются головные уборы трех видов (шляпы, панамы и бейсболки), сделанные из четырех материалов (брезент, хлопок, шелк и соломка). На диаграмме 1 показано количество головных уборов каждого вида, а на диаграмме 2 — распределение головных уборов по материалам.
Диаграмма 1 диаграмма 2
50
![]() 45
45
40
35Брезент зо• Хлопок 25
20О Шелк
15Соломка
10
5
шляпы Панамы Бейсболки
Какое из следующих утверждений следует из анализа обеих диаграмм?
1) Все соломенные изделия могут быть бейсболками.
2) Все панамки могут быть из хлопка или брезента.
З) Среди изделий из шелка может не быть ни одной шляпы.
4) Среди изделий, сделанных не из соломки, может не быть ни одной панамы.
Решение
Используя данные из диаграммы 1 , вычислим общее количество головных уборов:
45 + 35 + 20 = 100 (головных уборов).
Таким образом, согласно диаграмме 2, количество головных уборов из брезента и хлопка одинаково, количество головных уборов из соломки равно числу головных уборов из брезента и хлопка, а головных уборов из шелка столько же, сколько всех остальных вместе взятых.
Сопоставив полученные значения с имеющимися высказываниями и с данными из диаграмм, получим, что среди изделий из шелка может не быть ни одной шляпы. Значит, верным является третий вариант ответа.
Номер ответа: З.
Системы управления базами данных.
Организация баз данных
1. Результаты тестирования представлены в таблице:
|
Фамилия пол |
Мате- матика |
Русский язык |
Химия |
Информатика |
Биология |
|
|
Аганян |
|
|
56 |
46 |
32 |
70 |
|
Воронин |
м |
43 |
62 |
45 |
74 |
23 |
|
Григорчук |
м |
54 |
74 |
68 |
75 |
83 |
|
Роднина |
|
71 |
63 |
56 |
82 |
79 |
|
Сергеенко |
|
33 |
25 |
74 |
38 |
46 |
|
Черепанова |
ж |
18 |
92 |
83 |
28 |
61 |
Решение
Высказывание пол= ж ' истинно для записей 1, 4, 5 и 6. Высказывание Химия>Биология истинно для записей 2, 5 и 6. Значит, высказывание пол— ' ж ' ИЛИ химия > Биология истинно для записей 1, 2, 4, 5 и 6, т. е. для пяти записей.
Для решения данного задания также возможно построение табЛИЦЫ истинности:
|
Номер записи |
пог.='ж' |
Химия > Биология |
пол='ж' или ХИмия > Биология |
|
1 |
1 |
|
1 |
|
2 |
|
1 |
1 |
|
З |
О |
|
|
|
4 |
1 |
о |
1 |
|
5 |
1 |
1 |
1 |
|
6 |
1 |
1 |
1 |
1.
2. Сколько записей в нижеследующем фрагменте турнирной таблицы удовлетворяют условию место <= 4 И (Н > 2 ИЛИ О > б) ?
|
Место |
Участник |
в |
н |
п |
О |
|
1 |
Силин |
5 |
З |
1 |
|
|
2 |
Клеменс |
6 |
о |
З |
6 |
|
З |
Холево |
5 |
1 |
4 |
|
|
4 |
Яшвили |
з |
5 |
1 |
|
|
5 |
Бергер |
з |
з |
З |
|
|
6 |
Численко |
з |
2 |
4 |
4 |
Решение
Высказывание Место <= 4 истинно для записей 1, 2, З и 4. Высказываниен > 2 истинно для записей 1, 4 и 5. ВысказываниеО > б истинно для записи 1. Значит, высказывание место <= 4 И (Н > 2 ИЛИ О > 6) истинно для записей 1 и 4, т. е. для двух записей.
Номер ответа: 2.
|
Место |
Команда |
в |
н |
п |
о |
мз |
мп |
|
1 |
Боец |
5 |
з |
1 |
18 |
9 |
5 |
|
2 |
Авангард |
6 |
О |
з |
|
|
7 |
|
З |
Опушка |
4 |
1 |
4 |
|
|
7 |
|
|
Звезда |
з |
6 |
о |
15 |
5 |
2 |
|
5 |
Химик |
з |
з |
з |
12 |
14 |
17 |
|
6 |
Пират |
З |
2 |
4 |
11 |
13 |
7 |
Решение
Высказывание место <= 5 истинно для записей 1, 2, З, 4 и 5. Высказывание В > 4 истинно для записей 1 и 2. Высказывание МЗ > 12 истинно для записей 2, З, 5 и 6. Значит, высказывание место <= 5 и (В > 4 ИЛИ мз > 12) истинно для записей 1, 2, З и 5,
т. е. для четырех записей.
4.
|
|
Страна |
Столица |
площадь, 2 тыс. км |
Численность населения, тысяч чел. |
Часть света |
|
1 |
Бельгия |
Брюссель |
30,5 |
10 289 |
Европа |
|
2 |
Бурунди |
Бужумбура |
27,8 |
6 096 |
Африка |
|
З |
Гаити |
Порт-о-Пренс |
27,8 |
7 528 |
Северная Америка |
|
4 |
Дания |
Копенгаген |
43,1 |
5 384 |
Европа |
|
5 |
Джибути |
Джибути |
22,0 |
0,457 |
Африка |
|
6 |
Доминикан- ская Республика |
СантоДоминго |
48 |
8 716 |
Северная Америка |
|
7 |
Израиль |
Иерусалим |
20,8 |
6 116 |
Азия |
|
8 |
Коста-Рика |
Сан-Хосе |
51,1 |
з 896 |
Северная Америка |
|
9 |
Лесото |
Масеру |
30,4 |
1 862 |
Африка |
|
10 |
Македония |
Скопье |
25,3 |
2 063 |
Европа |
|
11 |
Руанда |
Кигали |
26,4 |
7 810 |
Африка |
|
12 |
Сальвадор |
Сан-Сальвадор |
21,0 |
6 470 |
Северная Америка |
Сколько записей в данном фрагменте удовлетворяют условию:
( (Площадь, тыс . км Е > 30) И (Численность населения, тысяч чел. :::> 5000) ) И (Часть света Европа) ?
Решение
Высказывание Площадь, тыс . км[• 30 истинно для записей 1, 4, 6, 8 и 9. Высказывание Численность населения, тысяч чел. > 5000 истинно для записей 1, 2, З, 4, 6, 7, 11 и 12. Высказывание Часть света Европа истинно для записей 1, 4 и 10. Значит, высказывание ( (Площадь, тыс . > 30) И (Численность насе— ления, тысяч чел . > 5000) ) И (Часть света = Европа) истинно для записей 1 и 4, т. е. для двух записей. 2.
5. На олимпиаде по английскому языку предлагались задания трех типов: А, В и С. Итоги олимпиады были оформлены в таблицу, в которой было отражено, сколько заданий каждого типа выполнил каждый участник, например:
|
Фамилия, имя участника |
А |
в |
с |
|
Быкова Елена |
з |
1 |
1 |
|
Тихомиров Сергей |
|
2 |
1 |
За правильное выполнение задания типа А участнику начислялся 1 балл, за выполнение задания типа В — З балла и за С — 5 баллов. Победитель определялся по сумме набранных баллов. При этом у всех участников сумма баллов оказалась разной. Для определения победителя олимпиады достаточно выполнить следующий запрос:
1) Отсортировать таблицу по убыванию значения столбца С и взять первую строку.
2)
З) Отсортировать таблицу по убыванию значений выражения А + ЗВ + 5С и взять первую строку. 4) Отсортировать таблицу по возрастанию значений выражения А + ЗВ + 5С и взять первую строку.
Решение
Поскольку победитель определялся по сумме набранных баллов, сортировка по убыванию значения столбца С не даст нужных результатов.
Так как задания разного типа оцениваются различным количеством баллов, сортировка таблицы по возрастанию значений выражения А + В + С тоже не даст нужных результатов.
Поскольку за правильное выполнение задания типа А участнику начислялся 1 балл, за выполнение задания типа В — З балла и за С — 5 баллов, необходимо осуществить сортировку таблицы по убыванию значений выражения А + ЗВ + 5С и взять первую строку. Номер ответа: З.
6. Ниже в табличной форме представлен фрагмент базы данных:
|
№ п/п |
Наименование товара |
Цена |
Количество |
Стоимость |
|
1 |
Монитор |
7654 |
20 |
153 080 |
|
2 |
Клавиатура |
1340 |
26 |
34 840 |
|
З |
Мышь |
235 |
|
7 990 |
|
4 |
Принтер |
3770 |
8 |
22 620 |
|
5 |
Колонки акустические |
480 |
16 |
7 680 |
|
6 |
Сканер планшетный |
2880 |
10 |
28 800 |
На какой позиции окажется товар «Сканер планшетный», если произвести сортировку данной таблицы по возрастанию столбца « Количество » ?
![]()
Решение
Если произвести сортировку данной таблицы по возрастанию столбца «Количество», то товары будут располагаться в следующем порядке: 4, 6, 5, 1, 2, З. Таким образом, товар «Сканер планшетный» окажется на второй позиции. Номер ответа: 2.
7.
|
|
Название пролива |
Длина (км) |
Ширина (км) |
Глубина (м) |
Местоположение |
|
1 |
Босфор |
зо |
|
20 |
Атлантический океан |
|
2 |
Магелланов |
575 |
2,2 |
29 |
Тихий океан |
|
З |
Ормузский |
195 |
54 |
27 |
Индийский океан |
|
4 |
Гудзонов |
806 |
115 |
141 |
Северный Ледовитый океан |
|
5 |
Гибралтарский |
59 |
14 |
53 |
Атлантический океан |
|
6 |
Ла-Манш |
578 |
32 |
23 |
Атлантический океан |
|
7 |
Баб-эльМандебский |
109 |
26 |
31 |
Индийский океан |
|
8 |
Дарданеллы |
120 |
1,3 |
29 |
Атлантический океан |
|
9 |
Берингов |
96 |
86 |
36 |
Тихий океан |
Сколько записей в данном фрагменте удовлетворяют условию:
(Ширина (км) > 50 ИЛИ Глубина (м) > 50) И (Местоположение = Атлантический океан) ?
Решение
Высказывание Ширина (км) > 50 истинно для записей З, 4 и 9. Высказывание Глубина (м) > 50 истинно для записей 4 и 5. Высказывание местоположение = Атлантический океан истинно для записей 1, 5, 6 и 8. Значит, высказывание (Ширина (км) > 50 ИЛИ Глубина (м) > 50) И (Местоположение = Атлантический океан) истинно для записи 5, т. е. для одной записи. Номер ответа: 1.
8.
|
Фамилия |
Имя |
Пол |
Год рождения |
Рост (см) |
Вес (кг) |
|
Соколова |
Елена |
|
1990 |
165 |
51 |
|
Антипов |
Ярослав |
м |
1989 |
170 |
53 |
|
Дмитриева |
Елена |
|
1990 |
161 |
|
|
Коровин |
Дмитрий |
м |
1990 |
178 |
60 |
|
Зубарев |
Роман |
м |
1991 |
172 |
58 |
|
Полянко |
Яна |
|
1989 |
170 |
49 |
Сколько записей в данном фрагменте удовлетворяют условию: (Имя — ' Елена ИЛИ (Год рождения > 1989) ?
![]()
Решение
Высказывание имя ' Елена ' истинно для записей 1 и З. Высказывание год рождения > 1989 истинно для записей 1, З, 4 и 5. Значит, высказывание (Имя ' Елена ' ) ИЛИ (Год рождения > 1989) истинно для записей 1, З, 4 и 5, т. е. для четырех записей. Номер ответа: 4.
9.
|
|
Страна |
Столица |
пло- щадь, 2 тыс. км |
Численность населения, тысяч чел. |
Часть света |
|
1 |
Бельгия |
Брюссель |
30,5 |
10 289 |
Европа |
|
2 |
Бурунди |
Бужумбура |
27,8 |
6 096 |
Африка |
|
З |
Гаити |
Порт-о-Пренс |
27,8 |
7 528 |
Северная Америка |
|
4 |
Дания |
Копенгаген |
43,1 |
5 384 |
Европа |
|
5 |
Джибути |
Джибути |
22,0 |
0,457 |
Африка |
|
6 |
Доминикан- ская Республика |
СантоДоминго |
48 |
8 716 |
Северная Америка |
|
7 |
Израиль |
Иерусалим |
20,8 |
6 116 |
Азия |
|
8 |
Коста-Рика |
Сан-Хосе |
51,1 |
з 896 |
Северная Америка |
|
9 |
Лесото |
Масеру |
30,4 |
1 862 |
Африка |
|
10 |
Македония |
Скопье |
25,3 |
2 063 |
Европа |
|
11 |
Руанда |
Кигали |
26,4 |
7 810 |
Африка |
|
12 |
Сальвадор |
Сан-Сальвадор |
21,0 |
6 470 |
Северная Америка |
Сколько записей в данном фрагменте удовлетворяют условию: ( (Площадь, тыс. км ) > 20) И (Численность населения, тысяч чел. ) > 1500) ) И (Часть света = Африка)?
![]()
Решение
Высказывание (Площадь, тыс. > 20 истинно для всех записей. Высказывание (Численность населения, тысяч чел. ) > 1500 истинно для записей 1, 2, З, 4, 6, 7, 8, 9, 10, 11 и 12. Высказывание Часть света = Африка истинно для записей 2, 5, 9, и 11. Значит, высказывание ( (Площадь, тыс. км Е ) > 20) И (Численность на— селения, тысяч чел. ) > 1500) ) И (Часть света = Африка) истинно для записей 2, 9, и 11, т. е. для трех записей. Номер ответа: З.
10. Ниже в табличной форме представлен фрагмент базы данных:
|
Номер |
Фамилия |
Имя |
Отчество |
Класс |
Школа |
|
1 |
Иванов |
Петр |
Олегович |
10 |
135 |
|
2 |
Катаев |
Сергей |
Иванович |
9 |
195 |
|
З |
Беляев |
Иван |
Петрович |
11 |
45 |
|
4 |
Носов |
Антон |
Павлович |
7 |
4 |
Какую строку будет занимать фамилия «Иванов» после проведения сортировки по возрастанию в поле «Класс» ?
Решение
Если произвести сортировку данной таблицы по возрастанию в поле «класс», то фамилии будут располагаться в следующем порядке: 4, 2, 1, З. Таким образом, фамилия «Иванов» окажется на третьей позиции.
Номер ответа: З.
11.
|
Номер |
Фамилия |
Пол |
Алгебра |
Сочинение |
Физика |
История |
|
1 |
Аверин |
м |
5 |
4 |
5 |
з |
|
2 |
Антонов |
м |
З |
5 |
4 |
5 |
|
З |
Васильева |
|
З |
5 |
4 |
5 |
|
4 |
Купанов |
м |
4 |
5 |
4 |
5 |
|
5 |
Лебедева |
|
4 |
З |
з |
4 |
|
6 |
Прокопьев |
м |
|
2 |
4 |
з |
Сколько записей удовлетворяют условию:
(Пол ' ж ' ) ИЛИ (Физика < 5 ИЛИ Алгебра = 4) ?
Решение
Высказывание пол ' ж ' истинно для записей З и 5.
Высказывание Физика < 5 истинно для записей 2, З, 4, 5, 6. Высказывание
Алгебра = 4 истинно для записей 4 и 5. Значит, высказывание (Пол ![]() ' ж ' ) ИЛИ (Физика < 5 ИЛИ
Алгебра = 4) истинно для записей 2, З, 4, 5 и 6, т. е. для пяти записей. Номер
ответа: 1.
' ж ' ) ИЛИ (Физика < 5 ИЛИ
Алгебра = 4) истинно для записей 2, З, 4, 5 и 6, т. е. для пяти записей. Номер
ответа: 1.
12.
|
Фамилия |
пол |
Баллы за задачи |
|
|||||
|
1 |
2 |
|
4 |
5 |
6 |
7 |
||
|
Айвазян Г. |
ж |
1 |
о |
2 |
1 |
о |
1 |
З |
|
Викторов М. |
м |
2 |
2 |
2 |
2 |
2 |
1 |
4 |
|
Гордезиани Б. |
м |
2 |
|
|
|
|
1 |
4 |
|
Михальчук М. |
м |
1 |
1 |
1 |
1 |
1 |
2 |
|
|
Пай С. |
м |
2 |
О |
О |
|
|
|
|
|
Шапсугов М. |
м |
2 |
2 |
|
|
|
|
|
|
Юльченко М. |
ж |
1 |
1 |
|
|
|
|
з |
|
Яковлева К. |
ж |
2 |
2 |
О |
о |
1 |
1 |
з |
Сколько человек прошли на городской тур?
Решение
На городской тур олимпиады по ОБЖ пройдут учащиеся Викторов М., Гордезиани Б. и Пай С., поскольку они решили полностью одну из самых сложных задач N2N2 6 или 7. Кроме того, Михальчук М. и Шапсугов М. набрали на районном туре не менее 10 баллов. Таким образом, на городской тур пройдут 5 человек.
Номер ответа: 1.
13. Ниже приведены фрагменты таблиц базы данных участников конкурса исполнительского мастерства:
|
|
|
Представители скольких стран исполняют произведения Моцарта?
Решение
Воспользовавшись данными из второй таблицы, выявим участников, исполняющих произведения Моцарта. Это Альбрехт, Силин, Холево, Численко и Яшвили,
Определим страны, которые представляют эти участники:
![]() Альбрехт
— Германия;
Альбрехт
— Германия;
![]()
![]() Холево
— Россия;
Холево
— Россия;
![]() Численко — Украина; е Яшвили —
Грузия.
Численко — Украина; е Яшвили —
Грузия.
Таким образом, указанные пять участников представляют четыре страны: Германию, Россию, Украину и Грузию.
Номер ответа: 4.
13. На игровом Интернет-сайте есть следующая информация об играх и количестве играющих:
|
Аркадные |
Логические |
Словесные |
Спортивные |
|||
|
Астероид Веселая ферма Фабрика подарков |
Фишдом Филлер Снежные загадки |
Виселица Сканворд Лесопилка |
Бильярд Боулинг Футбол |
|||
|
Игра |
Кол-во играющих |
|
|||
|
Астероид |
536 |
|
|||
|
Бильярд |
34О |
|
|||
|
Боулинг |
60 |
|
|||
|
Веселая ферма |
264 |
|
|||
|
Виселица |
981 |
|
|||
|
Лесопилка |
288 |
|
|||
|
Сканворд |
119 |
|
|||
|
Снежные загадки |
93 |
|
|||
|
Фабрика подарков |
100 |
|
|||
|
Филлер |
46з |
|
|||
|
Фишдом |
437 |
|
|||
|
Футбол |
572 |
|
|||
Определите, игры какого типа пользуются наибольшей популярностью у игроков (в игры какого типа играет наибольшее количество людей)?
1) Аркадные
2) Логические З) Словесные 4) Спортивные
Решение
Таким образом, наибольшей популярностью у игроков пользуются словесные игры.
Номер ответа: З.
14. На игровом Интернет-сайте есть следующая информация об играх и количестве играющих:
|
Аркадные |
Логические |
Словесные |
Спортивные |
|||
|
Астероид Веселая ферма Фабрика подарков |
Фишдом Филлер Снежные загадки |
Виселица Сканворд Лесопилка |
Бильярд Боулинг Футбол |
|||
|
Игра |
Кол-во играющих |
|
|||
|
Астероид |
536 |
|
|||
|
Бильярд |
340 |
|
|||
|
Боулинг |
60 |
|
|||
|
Веселая ферма |
264 |
|
|||
|
Виселица |
981 |
|
|||
|
Лесопилка |
288 |
|
|||
|
Сканворд |
119 |
|
|||
|
Снежные загадки |
93 |
|
|||
|
Фабрика подарков |
100 |
|
|||
|
Филлер |
463 |
|
|||
|
Фишдом |
437 |
|
|||
|
Футбол |
572 |
|
|||
Определите, игры какого типа чаще всего встречаются в пятерке
самых популярных игр.
1) Аркадные
2) Логические З) Словесные 4) Спортивные
Решение
Воспользовавшись данными из этих таблиц, определим, игры какого типа чаще всего встречаются в пятерке самых популярных игр:
• Виселица — 981 играющий — словесная игра;
• Футбол — 572 играющих — спортивная игра;
• Астероид — 536 играющих — аркадная игра;
• Филлер — 463 играющих — логическая игра;
• Фишдом — 437 играющих — логическая игра.
Таким образом, в пятерке самых популярных игр чаще всего встречаются логические игры. Номер ответа: 2.
15.
|
Школа |
Фамилия |
|
Фамилия |
Предмет |
Диплом |
|
10 |
Иванов |
Иванов |
физика |
I степени |
|
|
10 |
Петров |
Мискин |
математика |
III степени |
|
|
10 |
Сидоров |
Сидоров |
физика |
П степени |
|
|
50 |
Кошкин |
Кошкин |
история |
степени |
|
|
№ 150 |
Ложкин |
Ложкин |
физика |
П степени |
|
|
150 |
Ножкин |
Ножкин |
история |
I степени |
|
|
№ 200 |
Тарелкин |
Тарелкин |
физика |
III степени |
|
|
№ 200 |
Мискин |
Петров |
история |
I степени |
|
|
№ 250 |
Чашкин |
Мискин |
физика |
I степени |
Сколько дипломов I степени получили ученики 10-й школы?
Решение
Воспользовавшись данными из первой таблицы, выявим учащихся школы N2 10: это Иванов, Петров и Сидоров. Определим, дипломы какой степени получили эти школьники:
![]() Иванов — диплом I степени;
Иванов — диплом I степени; ![]() Петров — диплом I
степени;
Петров — диплом I
степени;
![]() Сидоров
— диплом П степени.
Сидоров
— диплом П степени.
Таким образом, ученики школы .N2 10 получили два диплома I степени.
Номер ответа: 2.
16.
|
Код класса |
Класс |
|
Фамилия |
Код класса |
Рост |
|
1 |
|
Иванов |
|
156 |
|
|
2 |
|
Петров |
5 |
174 |
|
|
з |
|
Сидоров |
8 |
135 |
|
|
4 |
|
Кошкин |
з |
148 |
|
|
5 |
|
Ложкин |
2 |
134 |
|
|
6 |
|
Ножкин |
8 |
183 |
|
|
7 |
|
Тарелкин |
5 |
158 |
|
|
8 |
|
Мискин |
2 |
175 |
|
|
9 |
1ОА |
Чашкин |
|
169 |
В каком классе учится самый высокий ученик?
1) ЗА
Решение
Воспользовавшись второй таблицей, определим самого высокого учащегося: это Ножкин, рост 183 см, код класса — 8. Этот код соответствует 9А классу.
Номер ответа: 4.
17. Ниже приведены фрагменты таблиц базы данных канцелярского магазина:
|
|
|
Сколько разных видов карандашей продается в магазине?
Решение
Воспользовавшись данными из первой таблицы, определим артикулы карандашей: 3647 и 8457. Далее определим, сколько разных видов карандашей продается в магазине: е 8457 — красный; , 3647 —синий; , 3647—зеленый; о 3647 — красный.
Таким образом, в магазине продаются четыре разных вида карандашей.
Номер ответа: 4.
18.
|
Школа |
Фамилия |
|
Фамилия |
Предмет |
Диплом |
|
№ 10 |
Иванов |
Иванов |
физика |
степени |
|
|
М 10 |
Петров |
Мискин |
математика |
III степени |
|
|
№ 10 |
Сидоров |
Сидоров |
физика |
П степени |
|
|
№ 50 |
Кошкин |
Кошкин |
история |
I степени |
|
|
150 |
Ложкин |
Ложкин |
физика |
П степени |
|
|
№ 150 |
Ножкин |
Ножкин |
история |
I степени |
|
|
Г.Г2 200 |
Тарелкин |
Тарелкин |
физика |
III степени |
|
|
.N2 200 |
Мискин |
Петров |
история |
I степени |
|
|
250 |
Чашкин |
Мискин |
физика |
I степени |
Сколько различных школ имеют победителей олимпиады по физике?
Решение
Воспользовавшись данными из второй таблицы, определим фамилии победителей олимпиады по физике: это Иванов, Сидоров, Ложкин, Тарелкин и Мискин. Определим номера школ, в которых учатся эти школьники:
![]() Иванов
Иванов![]()
![]() Сидоров
Сидоров![]()
![]() Ложкин №
150;
Ложкин №
150;
![]() Тарелкин —
Тарелкин —
![]() Мискин
— .N2 200.
Мискин
— .N2 200.
Таким образом, победителями олимпиады по физике являются
ученики трех различных школ. Номер ответа: З.
19. Ниже приведены фрагменты таблиц базы данных учеников школы:
|
Код класса |
Класс |
|
Фамилия |
Код класса |
Рост |
|
1 |
|
Иванов |
З |
156 |
|
|
2 |
ЗА |
Петров |
5 |
174 |
|
|
з |
|
Сидоров |
8 |
135 |
|
|
4 |
|
Кошкин |
З |
148 |
|
|
5 |
|
Ложкин |
2 |
134 |
|
|
6 |
|
Ножкин |
8 |
183 |
|
|
7 |
|
Тарелкин |
5 |
158 |
|
|
8 |
|
Мискин |
2 |
175 |
|
|
9 |
1ОА |
Чашкин |
з |
169 |
В каком классе учится наибольшее число учеников?
Решение
Воспользовавшись данными из второй таблицы, определим код класса, в котором учится наибольшее число учеников: З. Таким образом, наибольшее число учеников — в 4А классе. Номер ответа: 2.
20. Ниже приведены фрагменты таблиц базы данных канцелярского магазина:
|
|
|
Сколько разных (по названию) красных изделий продается в магазине?
![]()
Решение
Согласно данным из этих таблиц, артикулы красных изделий таковы: 8457 — карандаш, 3647 — карандаш, 1948 — авторучка. Таким образом, в магазине продается два разных (по названию)
красных изделия.
Номер ответа: 2.
21.
|
|
|
В каком классе наибольший рост у самого низкого ученика в классе?
1) ЗА
Решение
Согласно данным из второй таблицы, наибольший рост — у самого низкого ученика, имеющего код класса 5. Тогда, согласно данным из второй таблицы, этот школьник учится в 6А классе. Номер ответа: З.
22. Ниже приведены фрагменты таблиц базы данных канцелярского магазина:
|
|
|
За какую самую низкую цену в магазине можно купить карандаш?
Решение
1. В таблице приведены запросы к поисковому серверу. Расположите номера этих запросов по возрастанию количества страниц, которые поисковый сервер найдет по каждому запросу. Для обозначения логической операции ИЛИ в запросе используется символ , а для логической операции И — 8.
|
|
Запрос |
|
1 |
канарейки щеглы содержание |
|
2 |
канарейки & содержание |
|
З |
канарейки & щеглы & содеожание |
|
4 |
разведение & содержание & канаоейки & щеглы |
Решение
Больше всего будет найдено страниц по запросу 1, так как при его выполнении будут найдены страницы и со словом «канарейки» , и со словом «щеглы» , и со словом «содержание» .
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу всех четырех слов: «разведение», «содержание», «канарейки» и «щеглы» .
По запросу З будут найдены все страницы, содержащие слова «канарейки», «щеглы» и «содержание», — их будет больше, чем страниц, найденных по запросу 4.
По запросу 2 будет найдено больше страниц, чем по запросу З, но меньше, чем по запросу 1.
Искомая последовательность номеров запросов: 4321.
Ответ: 4321.
|
|
|
Запрос |
|
1 |
принтеры |
сканеры & продажа |
|
2 |
принтеры |
продажа |
|
з |
принтеры |
продажа |
|
4 |
принтеры |
сканеры продажа |
Решение
Больше всего будет найдено страниц по запросу 4, так как при его выполнении будут найдены страницы и со словом «принтеры» , и со словом «сканеры», и со словом «продажа».
Меньше всего будет найдено страниц по запросу 1, так как в нем необходимо присутствие на искомой странице сразу всех трех слов: «принтеры», «сканеры» и «продажа» .
По запросу З будут найдены все страницы, содержащие хотя бы одно из слов: «принтеры» или «продажа» — их будет меньше, чем страниц, найденных по запросу 4.
По запросу 2 будет найдено больше страниц, чем по запросу 1 , но меньше, чем по запросу З.
Искомая последовательность номеров запросов: 1234.
Ответ: 1234.
З. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Количество сайтов, для которых данное слово является ключевым |
|
сканер |
200 |
|
принтер |
250 |
|
монитор |
450 |
Сколько сайтов будет найдено по запросу:
(принтер сканер) & монитор если по запросу принтер сканер было найдено 450 сайтов, по запросу принтер & монитор — 40, а по запросу сканер & монитор — 50.
Решение
4. В таблице приведены запросы к поисковому серверу. Расположите номера этих запросов по возрастанию количества страниц, которые поисковый сервер найдет по каждому запросу. Для обозначения логической операции ИЛИ в запросе используется символ , а для логической операции И — & .
|
|
Запрос |
|
1 |
физкультура |
|
2 |
физкультура & подтягивания & отжимания |
|
з |
физкультура & подтягивания |
|
4 |
физкуль тура фитнес |
Решение
Больше всего будет найдено страниц по запросу 4, так как при его выполнении будут найдены страницы и со словом «физкультура», и со словом «фитнес» .
Меньше всего страниц по запросу 2, так как в нем необходимо присутствие на искомой странице сразу всех трех слов: «физкультура», «подтягивание» и «отжимания» .
По запросу З будут найдены все страницы, содержащие слова «физкультура» и «подтягивания» , — их будет меньше, чем страниц, найденных по запросу 1.
Искомая последовательность номеров запросов: 2314. Ответ: 2314.
|
|
|
Запрос |
|
|
|
1 |
волейбол |
баскетбол |
подача |
|
|
2 |
волейбол |
баскетбол |
подача |
I блок |
|
З |
волейбол |
баскетбол |
|
|
|
4 |
волейбол |
баскетбол |
подача |
|
Решение
Больше всего будет найдено страниц по запросу 2, так как при его выполнении будут найдены страницы и со словом «волейбол», и со словом «баскетбол», и со словом «подача», и со словом «блок».
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу всех трех слов: «волейбол», «баскетбол» и «подача» .
По запросу 1 будут найдены все страницы, содержащие любое из слов «волейбол», «баскетбол» и «подача», — их будет больше, чем страниц, найденных по запросу З.
По запросу З будет найдено больше страниц, чем по запросу 4.
Искомая последовательность номеров запросов: 4312. Ответ: 4312.
6. В таблице приведены запросы к поисковому серверу. жите номера этих запросов по возрастанию количества
|
торые |
найдет по |
запросу. |
|
|||
|
ния |
в |
|
|
|||
|
а для |
— |
|
|
|||
|
|
|
Запрос |
|||
|
1 |
чемпионы |
(бег & плавание) |
|||
|
2 |
чемпионы |
& плавание |
|||
|
з |
чемпионы |
бег плавание |
|||
|
4 |
чемпионы |
& Европа & бег & |
|||
Решение
Больше всего будет найдено страниц по запросу З, так как при его выполнении будут найдены страницы и со словом «чемпионы» , и со словом «бег», и со словом «плавание» .
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу всех четырех слов: «чемпионы», «Европа», «бег» и «плавание».
По запросу 1 будут найдены все страницы, содержащие слова «чемпионы» или оба слова «бег» и «плавание», — их будет больше, чем страниц, найденных по запросу 2.
По запросу 2 будет найдено больше страниц, чем по запросу 4.
Искомая последовательность номеров запросов: 4213. Ответ: 4213.
|
|
|
Запрос |
|
|
1 |
музыка |
классика Моцарт |
серенада |
|
2 |
музыка |
классика |
|
|
З |
музыка |
классика Моцарт |
|
|
4 |
музыка |
классика & Моцарт |
|
Решение
Больше всего будет найдено страниц по запросу 1, так как при его выполнении будут найдены страницы и со словом «музыка» , и со словом «классика», и со словом «Моцарт» , и со словом «серенада» .
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу всех трех слов: «музыка», «классика» и «Моцарт».
По запросу З все страницы, содержащие слова «музыка», «классика» и «Моцарт», — их будет больше, чем страниц, найденных по запросу 2, но меньше, чем по запросу 4.
Искомая последовательность номеров запросов: 4231. Ответ: 4231.
|
|
Запрос |
|
|
|
|
1 |
реферат |
математика |
I Гаусс |
|
|
2 |
реферат |
математика |
гаусс |
метод |
|
З |
реферат |
математика |
|
|
|
4 |
реферат |
& математика |
Гаусс |
|
Решение
Больше всего будет найдено страниц по запросу 2, так как при его выполнении будут найдены страницы и со словом «реферат» , и со словом «математика», и со словом «Гаусс», и со словом «метод».
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу всех трех слов: «реферат», «математика» и «Гаусс».
По запросу З будут найдены все страницы, содержащие слова «реферат» и «математика» , — их будет больше, чем страниц, найденных по запросу 4.
По запросу 1 будет найдено больше страниц, чем по запросу З, но меньше, чем по запросу 2.
Искомая последовательность номеров запросов: 4312. Ответ: 4312.
9. В таблице приведены запросы к поисковому серверу. жите номера этих запросов по возрастанию количества
|
торые |
найдет по |
запросу. |
|
||||
|
ния |
в |
|
|
||||
|
а для |
— |
|
|
||||
|
|
|
Запрос |
|
|||
|
1 |
Амеоика |
путешественники i Колумб |
|
|||
|
2 |
Амеоика |
путешественники Колумб |
открытие |
|||
|
З |
Америка |
Колумб |
|
|||
|
4 |
Америка |
путешественники & Колумб |
|
|||
Решение
Больше всего будет найдено страниц по запросу 2, так как при его выполнении будут найдены страницы и со словом «Америка», и со словом «путешественники», и со словом «Колумб», и со словом « открытие» .
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу всех трех слов: «Америка», «путешественники» и «Колумб» .
По запросу З будут найдены все страницы, содержащие слова «Америка» и «Колумб», — их будет больше, чем страниц, найденных по запросу 4.
По запросу 1 будет найдено больше страниц, чем по запросу З, но меньше, чем по запросу 2.
Искомая последовательность номеров запросов: 4312. Ответ: 4312.
|
|
|
Запрос |
|
|
1 |
Информатика |
уроки & Ехсе1 |
|
|
2 |
Информатика |
уроки Excel |
диаграмма |
|
З |
информатика |
уроки Excel |
|
|
4 |
Информатика |
Excel |
|
Решение
Больше всего будет найдено страниц по запросу 2, так как при его выполнении будут найдены страницы и со словом «Информатика», и со словом «уроки», и со словом «Excel», и со словом «диаграмма » .
Меньше всего страниц по запросу 1, так как в нем необходимо присутствие на искомой странице сразу всех трех слов: «Информатика», «уроки» и «Excel».
По запросу З будут найдены все страницы, содержащие слова «Информатика», «уроки» и «Excel», — их будет больше, чем страниц, найденных по запросу 4.
По запросу 4 будет найдено больше страниц, чем по запросу 1.
Искомая последовательность номеров запросов: 2341. Ответ: 2341.
|
|
Запрос |
|
1 |
Гренландия & Климат & Флора & Фауна |
|
2 |
Гренландия & Флора |
|
з |
(Гренландия & Флора) Фауна |
|
4 |
Гренландия & Флора & Фауна |
Решение
Больше всего будет найдено страниц по запросу З, так как при его выполнении будут найдены страницы со словами «Гренландия» и «Флора» или со словом «Фауна» .
Меньше всего будет найдено страниц по запросу 1, так как в нем необходимо присутствие на искомой странице сразу всех четырех слов: «Гренландия», «Климат», «Флора» и «Фауна».
По запросу 2 будут найдены все страницы, содержащие слова «Гренландия» и «Флора», — их будет больше, чем страниц, найденных по запросу 4.
По запросу 4 будет найдено больше страниц, чем по запросу 1.
Искомая последовательность номеров запросов: 1423. Ответ: 1423.
12. В таблице приведены запросы к поисковому серверу. ложите номера этих запросов по убыванию количества торые найдет по запросу. ния в а для — & .
13 ДергачеваЛ. М.
|
|
|
Запрос |
|
1 |
спорт |
футбол |
|
2 |
споот |
футбол Петербург Зенит |
|
з |
спорт |
футбол Петербург |
|
4 |
спорт |
футбол & Петербург & Зенит |
Решение
Больше всего будет найдено страниц по запросу 2, так как при его выполнении будут найдены страницы и со словом «спорт», и со словом «футбол», и со словом «Петербург», и со словом «Зенит» .
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу всех четырех слов: «спорт», «футбол», «Петербург» и «Зенит».
По запросу З будут найдены все страницы, содержащие слова «спорт», «футбол» и «Петербург», — их будет больше, чем страниц, найденных по запросу 1.
По запросу 1 будет найдено больше страниц, чем по запросу 1.
Искомая последовательность номеров запросов: 2314. Ответ: 2314.
|
Ключевое слово |
Количество сайтов, для которых данное слово является ключевым |
|
сомики |
250 |
|
меченосцы |
200 |
|
гуппи |
500 |
Сколько сайтов будет найдено по запросу:
сомики меченосцы гуппи, если по запросу сомики & гуппи было найдено О сайтов, по запросу сомики & меченосцы — 20, а по запросу меченосцы & гуппи — 10.
Решение
Для нахождения числа сайтов, найденных по запросу сомики ![]() меченосцы
гуппи, следует учесть, что 20 сайтов содержат слова «сомики» и «меченосцы» и 10
сайтов содержат слова «меченосцы»
меченосцы
гуппи, следует учесть, что 20 сайтов содержат слова «сомики» и «меченосцы» и 10
сайтов содержат слова «меченосцы»
и «гуппи». Тогда, согласно таблице ключевых слов, количество искомых сайтов равно:
250 + 200 + 500 - 20 - 10 - 920 (сайтов). Ответ: 920.
|
Ключевое слово |
Количество сайтов, для которых данное слово является ключевым |
|
сомики |
250 |
|
меченосцы |
200 |
|
гуппи |
500 |
Сколько сайтов будет найдено по запросу:
(сомики & меченосцы) гуппи, если по запросу сомики гуппи было найдено 750 сайтов, по запросу сомики & меченосцы — 100, а по запросу меченосцы & гуппи — О.
Решение
Для нахождения числа сайтов, найденных по запросу (сомики & меченосцы) гуппи, следует учесть, что ни один из сайтов не содержит слова «сомики» и «гуппи» одновременно, но 100 сайтов содержат слова «сомики» и «меченосцы». Тогда, согласно таблице ключевых слов, количество искомых сайтов равно:
100 + 500 — 600 (сайтов). Ответ: 600.
15. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Количество сайтов, для которых данное слово является ключевым |
|
Сканер |
200 |
|
Принтер |
250 |
|
Монитор |
450 |
Сколько сайтов будет найдено по запросу:
принтер сканер монитор, если по запросу принтер сканер было найдено 450 сайтов, по запросу принтер & монитор — 40, а по запросу сканер & монитор — 50. Решение
Для нахождения числа сайтов, найденных
по запросу принтер ![]() сканер монитор, следует учесть, что ни
один из сайтов не содержит слова «принтер» и «сканер» одновременно, 40 сайтов
содержат и слово «принтер», и слово «монитор», а 50 сайтов содержат и слово
«сканер», и слово «монитор». Тогда, согласно таблице ключевых слов, количество
искомых сайтов равно:
сканер монитор, следует учесть, что ни
один из сайтов не содержит слова «принтер» и «сканер» одновременно, 40 сайтов
содержат и слово «принтер», и слово «монитор», а 50 сайтов содержат и слово
«сканер», и слово «монитор». Тогда, согласно таблице ключевых слов, количество
искомых сайтов равно:
200+ 250 + 450 - 40 - 50 = 810 (сайтов). Ответ: 810.
|
ЛЕ |
Запрос |
|
|
1 |
(огурцы & помидоры) & (прополка |
поливка) |
|
2 |
огурцы помидоры |
|
|
з |
огурцы |
|
|
4 |
о г о цы поми д о РЫ |
|
Решение
Больше всего будет найдено страниц по запросу 2, так как при его выполнении будут найдены страницы и со словом «огурцы» , и со словом «помидоры» .
Меньше всего будет найдено страниц по запросу 1, так как в нем необходимо присутствие на искомой странице сразу всех слов: «огурцы» , «помидоры» и одного из слов «прополка» или «поливка» .
По запросу З будут найдены все страницы, содержащие слово «огурцы» ,— их будет больше, чем страниц, найденных по запросу 4.
2 по
1432. 1432.
17.
возрастанию количества страниц, поисковый сервер найдет по каждому запросу. Для обозначения логической операции ИЛИ в запросе используется символ , а для логической операции И — &.
|
|
Запрос |
|
1 |
экзамен тестирование |
|
2 |
(физика химия) & (экзамен тестирование) |
|
з |
физика & химия & экзамен & тестирование |
|
4 |
физика химия экзамен тестирование |
Решение
Меньше всего будет найдено страниц по запросу З, так как в нем необходимо присутствие на искомой странице сразу всех четырех слов: «физика», «химия», «экзамен» и «тестирование».
По запросу 1 будут найдены все страницы, содержащие слова «экзамен» или «тестирование», — их будет больше, чем страниц, найденных по запросу 2.
По запросу 2 будет найдено больше страниц, чем по запросу З.
Искомая последовательность номеров запросов: 3214. Ответ: 3214.
18. В таблице приведены запросы к поисковому серверу.
Расположите номера этих запросов по возрастанию количества страниц, которые
поисковый сервер найдет по каждому запросу. Для обозначения логической операции
ИЛИ в запросе используется символ , а для логической операции И —![]()
|
|
|
Запрос |
|
1 |
сомики |
меченосцы содержание |
|
2 |
сомики |
содержание |
|
З |
сомики |
меченосцы & разведение & содержание |
|
4 |
( СОМИКИ |
меченосцы) & содержание |
Решение
Больше всего будет найдено страниц по запросу 1, так как при его выполнении будут найдены страницы и со словом «сомики» , и со словом «меченосцы» , и со словом «содержание».
Меньше всего будет найдено страниц по запросу З, так как в нем необходимо присутствие на искомой странице сразу всех четырех слов: «сомики», «меченосцы», «разведение» и «содержание».
По запросу 2 будут найдены все страницы, содержащие слова «сомики» и «содержание» , — их будет больше, чем страниц, найденных по запросу З.
По запросу 4 будет найдено больше страниц, чем по запросу 2, но меньше, чем по запросу 1.
Искомая последовательность номеров запросов: 3241. Ответ: 3241.
|
|
|
Запрос |
|
1 |
барокко |
(классицизм & ампир) |
|
2 |
барокко |
классицизм |
|
З |
барокко |
ампир классицизм |
|
4 |
классицизм & ампио |
|
Решение
Больше всего будет найдено страниц по запросу З, так как при его выполнении будут найдены страницы и со словом «барокко» , и со словом «ампир», и со словом «классицизм» .
Меньше всего будет найдено страниц по запросу 4, так как в нем необходимо присутствие на искомой странице сразу двух слов: «классицизм» и «ампир».
По запросу 2 будут найдены все страницы, содержащие слова «барокко» и «классицизм», — их будет больше, чем страниц, найденных по запросу 1 .
1 по
3214. 3214.
20.
убыванию количества страниц, копоисковый сервер найдет по каждому запросу. Для обозначения логической операции ИЛИ в запросе используется символ , а для логической операции И — &.
|
|
Запрос |
|
1 |
зайцы & кролики |
|
2 |
зайцы & ( кролики лисицы) |
|
З |
зайцы & кролики & лисицы |
|
4 |
кролики лисицы |
Решение
Меньше всего будет найдено страниц по запросу З, так как в нем необходимо присутствие на искомой странице сразу трех слов: «зайцы», «кролики» и «лисицы».
По запросу 1 будут найдены все страницы, содержащие слова «зайцы» и «кролики», — их будет больше, чем страниц, найденных по запросу З.
По запросу 2 будет найдено больше страниц, чем по запросу 1.
Искомая последовательность номеров запросов: 4213.
Ответ: 4213.
21. В таблице приведены запросы к поисковому серверу. Расположите номера этих запросов по возрастанию количества страниц, которые поисковый сервер найдет по каждому запросу. Для обозначения логической операции ИЛИ в запросе используется символ , а для логической операции И — &.
|
|
Запрос |
|
1 |
кролики лисицы |
|
2 |
(зайцы & кролики) (лисицы & волки) |
|
з |
зайцы & кролики & лисицы & волки |
|
4 |
зайцы & кролики |
Решение
Больше всего будет найдено страниц по запросу 1, так как при его выполнении будут найдены страницы и со словом «кролики», и со словом «лисицы» .
Меньше всего будет найдено страниц по запросу З, так как в нем необходимо присутствие на искомой странице сразу четырех слов: «зайцы», «кролики», «лисицы» и «волки».
По запросу 4 будут найдены все страницы, содержащие слова «зайцы» и «кролики», — их будет больше, чем страниц, найденных по запросу З.
По запросу 2 будет найдено больше страниц, чем по запросу 4.
Искомая последовательность номеров запросов: 3421.
Ответ: 3421.
|
|
|
Запрос |
|
|
1 |
шка фы |
столы стулья |
|
|
2 |
шкафы |
(стулья & шкафы) |
|
|
З |
шка фы |
столы |
|
|
4 |
шкафы |
стулья |
Решение
Больше всего будет найдено страниц по запросу 1, так как при его выполнении будут найдены страницы и со словом «шкафы», и со словом «столы», и со словом «стулья» .
Меньше всего будет найдено страниц по запросу З, так как в нем необходимо присутствие на искомой странице сразу двух слов: «шкафы» и «стулья».
По запросу 4 будут найдены все страницы, содержащие слова «шкафы» или «стулья», — их будет больше, чем страниц, найденных по запросу 2.
2 по
3241.
3241.
23.
убыванию количества страниц,
копоисковый сервер найдет по каждому запросу. Для обозначения логической
операции ИЛИ в запросе используется символ , а для логической операции И —![]()
|
|
|
Запрос |
|
1 |
яблоки |
сливы |
|
2 |
сливы |
(сливы & груши) |
|
з |
яблоки |
груши сливы |
|
4 |
( яблоки |
груши) & сливы |
Решение
Меньше всего будет найдено страниц по запросу 4, так как при его выполнении будут найдены страницы и со словами «яблоки» или «груши», и со словом «сливы» .
Больше всего будет найдено страниц по запросу З, так как в нем необходимо присутствие одного из трех слов: «яблоки», «груши» или «сливы» на искомой странице.
По запросу 2 будет найдено больше страниц, чем по запросу 4. Искомая последовательность номеров запросов: 3124. ответ: 3124.
1. Определите, какое из указанных имен файлов
удовлетворяет маске: ![]()
1) he110. c
2) he110. срр
З) hhe1010. срр
4) hhe1010.c
Решение
Имя файла, удовлетворяющее маске 10 . с? *, должно содержать один произвольный символ, стоящий перед буквой h, следовательно, такое имя может быть представлено в вариантах ответа З и 4. Расширение также должно содержать произвольный символ, стоящий после буквы с, следовательно, маске ?hel * 10 . с? * удовлетворяет имя hhe1010. срр. З.
2. Перемещаясь из одного каталога в другой, пользователь последовательно посетил каталоги DOC, USER, SCHOOL, А: Х, LETTER, INBOX. При каждом перемещении пользователь либо спускался в каталог на один уровень ниже, либо поднимался на один уровень выше. Каково полное имя каталога, из которого пользователь начал перемещение?
1) А: \DOC

Решение
Пользователь мог последовательно посетить каталоги DOC, USER, SCHOOL и А : \ , только поднимаясь каждый раз на один уровень выше. Следующие каталоги — LETTER и INBOX — пользователь посетил, спускаясь на один уровень ниже. Таким образом, пользователь мог начать перемещение из каталога, полное имя которого
![]()
Номер ответа: З.
б) qq. срр
![]()
д) qaa . ста
е) q12 . срр
Определите, в каком порядке будут показаны файлы при выборе сортировки по типу (по возрастанию).
1) а в гдб е 2) ав гдеб З) а б в гд е 4) авд бе г
Решение
При сортировке по типу будут сравниваться расширения имен файлов. Если же расширения имен файлов совпадают, то используется дополнительная сортировка по имени. При этом отсутствие символа считается «меньшим», чем присутствие любого символа. Поэтому в результате файлы будут показаны в следующем порядке:
qaa . ста
q12 . срр
qq. С РР •
То есть порядок следования файлов будет таким: а в г д е б. Номер ответа: 2.
4. Для групповых операций с файлами используются маски
имен файлов. Маска представляет собой последовательность букв, цифр и прочих
допустимых в именах файлов символов, в которых также могут встречаться
следующие символы: ? (вопросительный знак) — обозначает ровно один произвольный
символ; * (звездочка) — обозначает любую последовательность символов
произвольной длины, в том числе пустую. Определите, какое из указанных имен
файлов удовлетворяет маске: ? а ? ? ? *![]()
1) dad1
2) dad22 З) 3daddy
4) add444
Решение
Номер ответа: 2.
5. В некотором каталоге хранился файл Задача 5. После того как в этом каталоге создали подкаталог и переместили в него файл Задача5, полное имя этого файла стало таким: Е : Х Класс 9\Физика \ Задачник х Задача 5. Каким было полное имя этого файла до его перемещения?
1)
Е : \физика![]()
2) Е: \Физика\Задача5
З) Е : \Класс9\Задачник\Задача5
4) Е : \Класс9\физика Х Задача 5
Решение
После перемещения файла Задача 5 в созданный подкаталог данный файл оказался в каталоге на один уровень ниже. Таким образом, полное имя файла до его перемещения: Е: \Класс9\Физика\ Задача5.
4.
6.
![]() Дано дерево каталогов. Определите полное имя файла Doc3:
1) А: \DOC3
Дано дерево каталогов. Определите полное имя файла Doc3:
1) А: \DOC3 
Решение
Файл Doc3 расположен в каталоге ТОМЗ на диске А. Таким образом, полное имя этого файла: А: \ТОМЗ \ Doc3. Номер ответа: 4.
7.
В некотором каталоге хранится файл список литературы. txt. В этом
каталоге создали подкаталог с именем 10 CLASS и переместили в него файл список
литературы. txt. После этого полное имя данного файла стало таким: D :![]()
10 CLASS\C11J4cok литературы. txt. Каким было полное имя каталога, в котором хранился файл до его перемещения?
![]() CLASS
CLASS
3) Г): \SCHOOL 4) SCHOOL
После перемещения файла список литературы. txt в созданный подкаталог данный файл оказался в каталоге на один уровень ниже. Таким образом, полное имя файла до его перемещения:
![]()
Номер ответа: 2.
8. Пользователь, перемещаясь из одного- каталога в другой, последовательно посетил каталоги LESSONS, CLASS, SCHOOL, D : Х, MYDOC, LETTERS. При каждом перемещении пользователь либо спускался в каталог на один уровень ниже, либо поднимался на один уровень выше. Каково полное имя каталога, из которого пользователь начал перемещение?
3)
![]() D : \LESSONS
D : \LESSONS![]()
4) Б: \LESSONS
Решение
Пользователь мог последовательно посетить каталоги LESSONS, CLASS, SCHOOL и D : Х, только поднимаясь каждый раз на один уровень выше. Следующие каталоги — MYDOC и LETTERS — пользова-
тель посетил, спускаясь на один уровень ниже. Таким образом, пользователь мог начать перемещение из каталога, полное имя которого
![]()
Номер ответа: 2.
9. В некотором каталоге хранится файл
Задачи_по_программированию . txt. В этом каталоге создали подкаталог и
переместили в него файл Задачи_по программированию. txt. После этого полное имя
данного файла стало таким:![]()
10 ![]() программированию . txt. Каким было полное имя каталога, в котором
хранился файл до его перемещения?
программированию . txt. Каким было полное имя каталога, в котором
хранился файл до его перемещения?
1) D: \INFORM
![]()
3) 10 CLASS
4) LESSONS\10 CLASS
Решение
Номер ответа: 2.
10. Учитель работал в каталоге D : \Материалы к урокам\ 10 класс Х Практические работы. Затем он перешел в дереве каталогов на один уровень выше, спустился в подкаталог Лекции и удалил из него файл Введение. Каково полное имя файла, который удалил преподаватель?
1) D : \Материалы к урокам \10 класс Х Введение
2) D : \Материалы к урокам \10 класс\Лекции\Введение
З) D : \Материалы к урокам\Лекции\Введение 4) D : Х Материалы к урокам\Введение\Лекции
Решение
После перемещения в каталог на один уровень выше преподаватель оказался в каталоге D : х Материалы к урокам \10 класс. Спустившись в подкаталог Лекции, он оказался в каталоге D : \Материалы к урокам класс Х Лекции. В подкаталоге Лекции находился файл Введение. Таким образом, полное имя файла, который удалил преподаватель: D : Х Материалы к урокам\10 класс\Лекции\ Введение.
2.
11. В некотором каталоге хранится файл
список 10 класса . txt. В этом каталоге создали подкаталог и переместили в него
файл список _10 класса . txt, после чего полное имя этого файла стало таким: D
: ![]() 10 класса. txt, Каким было полное имя
каталога, в котором хранился файл до перемещения?
10 класса. txt, Каким было полное имя
каталога, в котором хранился файл до перемещения?
![]()
2) DOC
![]()
4) CLASS
Решение
После перемещения файла список 10 класса . txt в созданный подкаталог данный файл оказался в каталоге на один уровень ниже. Таким образом, полное имя файла до перемещения:
![]()
Номер ответа: 1.
1) Е : \PROFESSOR \ACADEMY
3) Е : \ACADEMY
4)
Е : ![]() \ACADEMY
\ACADEMY
Решение
Преподаватель мог последовательно посетить каталоги ACADEMY
, COURSE, GROUP и Е: Х, только поднимаясь каждый раз на один уровень выше.
Следующие каталоги — PROFESSOR и LECTIONS — преподаватель посетил, спускаясь в
каталог на один уровень ниже. Таким образом, преподаватель мог начать
перемещение из каталога, полное имя которого — Е : ![]() \ACADEMY. Номер
ответа: 4.
\ACADEMY. Номер
ответа: 4.
13. Каталог содержит файлы с именами:
а) р5 .pas
б) р4 .ppt
в) p12 .pas
![]()
д) pq. pas
е) р 12 . ppt
Определите, в каком порядке будут показаны эти файлы при выборе сортировки по типу (по возрастанию).
1)вадгеб 2) гав дб е
З)вадгбе 4) гвадеб
Решение
При сортировке по типу будут сравниваться расширения имен файлов. Если же расширения имен файлов совпадают, то используется дополнительная сортировка по имени. При этом отсутствие символа считается «меньшим», чем присутствие любого символа. Поэтому в результате файлы будут показаны в следующем порядке:
Pq.P р 12 .pas р5 .pas pq . pas р 12 .ppt р4 . ppt
14. В некотором каталоге хранится файл
Шпора . txt. В этом каталоге создали подкаталог и переместили в него файл Шпора
. txt. После этого полное имя файла стало таким: D : Х Документы\ Физика ![]() Контрольная
\Шпора . txt. Каким было полное имя файла до его перемещения?
Контрольная
\Шпора . txt. Каким было полное имя файла до его перемещения?
1) D : \Документы\Контрольная\Шпора . txt
2) D : \Физика \Шпора . txt
З) D : \Документы\Физика Х Шпора . txt
4) D : Х Физика ![]() . txt
. txt
Решение
После перемещения файла Шпора . txt в созданный
подкаталог данный файл оказался в каталоге на один уровень ниже. Таким образом,
полное имя файла до перемещения: D : Х ![]() Шпора . txt.
Шпора . txt.
Номер ответа: З.
15. В некотором каталоге хранится файл Шпора . txt. В этом каталоге создали подкаталог и переместили в него файл Шпора . txt. После этого полное имя файла стало таким: D : \Документы\Химия\ Контрольная\Шпора . txt. Каким было полное имя каталога, в котором хранился файл до его перемещения?
![]()
2) D : \Документы\Химия
З) D : Х Документы
Решение
После перемещения файла Шпора . txt в созданный подкаталог данный файл оказался в каталоге на один уровень ниже. Таким образом, полное имя каталога до перемещения: D : \Документы\Химия. Номер ответа: 2.
16. Полное имя файла было: С : \Задачи\Физика . С. Его переместили в каталог Tasks корневого каталога диска D. Каким стало полное имя файла после его перемещения?
![]()
2) D : \Tasks \Физика.Е) З) D :
![]() 4) D : \Tasks .
С
4) D : \Tasks .
С
Решение
После перемещения файла Физика . С в каталог Tasks корневого каталога диска D полное имя файла стало: D : \Tasks х Физика . С. Номер ответа: 1.
17. Для групповых операций с файлами используются маски имен файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: ? (вопросительный знак) — обозначает ровно один произвольный символ; * (звездочка) — обозначает любую последовательность символов произвольной длины, в том числе пустую. Определите, какое из указанных имен файлов удовлетворяет маске: . ?xt.
1) bar . txt 2) obar . txt З) obar .xt
Решение
Имя файла, удовлетворяющее маске . ?xt, должно содержать
один произвольный символ, стоящий перед буквой Ь, следовательно, имя может быть
представлено в вариантах ответа 2 и З. Имя файла также должно содержать один
произвольный символ, стоящий перед буквой х в расширении файла, следовательно,
маске ![]() . ?xt удовлетворяет имя obar . txt. Номер
ответа: 2.
. ?xt удовлетворяет имя obar . txt. Номер
ответа: 2.
18. Находясь в корневом каталоге только что отформатированного диска, ученик создал три каталога. Затем в каждом имеющемся каталоге он создал еще по четыре каталога. Сколько всего каталогов, включая корневой, оказалось на диске?
2) 13
4) 16
Решение
Ученик создал в корневом каталоге только что отформатированного (т. е. пустого) диска три каталога, значит, общее количество каталогов стало равно четырем (включая изначально существовавший корневой). Затем в каждом из этих каталогов им было создано еще по четыре каталога. Таким образом, на диске оказалось 4 • 4 = 16 (каталогов), включая корневой. Номер ответа: 4.
2) Feetba11 . ddd З) Footba11 . mdb
4) Futb01 . doc
Решение
Имя файла, удовлетворяющее маске Е? ?tb* . d? * , должно содержать два произвольных символа, стоящих между буквами Е' и t, следовательно, имя может быть представлено в вариантах ответа 2 и З. Имя файла также должно содержать один произвольный символ, стоящий после буквы d в расширении файла, следовательно, маске Е? ?tb* . d? * удовлетворяет имя Feetba11 . ddd. Номер ответа: 2.
20. Для групповых операций с файлами используются маски имен файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: ? (вопросительный знак) обозначает ровно один произвольный символ; * (звездочка) обозначает любую последовательность символов произвольной длины, в том числе пустую. Определите, какое из указанных имен файлов удовлетворяет маске: A?ce*s . т * .
1) Acess .md
2) Accesst . dbf З) Access .mdb
4) Akcces . т 1
Решение
Имя файла, удовлетворяющее маске A?ce*s . должно содержать один произвольный символ, стоящий между буквами А и с. Кроме того, собственное имя файла должно оканчиваться буквой Е, следовательно, имя может быть представлено в вариантах ответа З и 4. Однако имя Akcces . т1 содержит лишний символ, не предусмотренный маской A?ce*s .т*, следовательно, маске A?ce*s .m* удовлетворяет имя Access . mdb. Номер ответа: З.
2) weprik. срр З) otopri . с
4) reprint .be
Решение
Имя файла, удовлетворяющее маске ??pri* э * , должно содержать два произвольных символа, стоящих перед буквой р, следовательно, это имя может быть представлено в вариантах ответа 1, 2 и 4. Поэтому маске ? ?pri * . не удовлетворяет имя otopri . с. Номер ответа: З.
22. Для групповых операций с файлами используются маски имен файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: ? (вопросительный знак) обозначает ровно один произвольный символ; * (звездоч-
![]()
ка) — обозначает
любую последовательность символов произвольной длины, в том числе пустую.
Определите, какое из указанных имен файлов не удовлетворяет маске: sys ? ? . *![]()
2) sys23 . ехе
З) system. d11
4) syszx . prob1em
Решение
Имя файла, удовлетворяющее маске sys?? . *, должно содержать два произвольных символа, стоящих после буквы s перед расширением файла, следовательно, это имя может быть представлено в вариантах ответа 1, 2 и 4. Поэтому маске sys ? ? . * не удовлетворяет имя system . d11.
Номер ответа: З.
23. Для групповых операций с файлами
используются маски имен файлов. Маска представляет собой последовательность
букв, цифр и прочих допустимых в именах файлов символов, в которых также могут
встречаться следующие символы: ? (вопросительный знак) — обозначает ровно один
произвольный символ; * (звездочка) — обозначает любую последовательность
символов произвольной длины, в том числе пустую. Определите, какое из указанных
имен файлов не удовлетворяет маске: ?ell * . ? ?![]()
1) уе11 .ow
З) te11 me .tu
4) Ье11 . -1аЬ
Решение
Имя файла, удовлетворяющее маске . ? ? , должно содержать только два произвольных символа, стоящих в расширении файла, следовательно, это имя может быть представлено в вариантах ответа 1, 2 и З. Поэтому маске ?е11* . ? ? не удовлетворяет имя be11 . 1ab.
Номер ответа: 4.
24. Для групповых операций с файлами используются маски имен
файлов. Маска представляет собой последовательность букв, цифр и прочих
допустимых в именах файлов символов, в которых также могут встречаться
следующие символы: ? (вопросительный знак) — обозначает ровно один произвольный
символ; * (звездочка) — обозначает любую последовательность символов
произвольной длины, в том числе пустую. Определите, какое из указанных имен
файлов не удовлетворяет маске: ? . t?*![]()
![]()
1) poydi . t
2) pogudi . tanx
З) 2di . t9 4) me10di . theme Решение:
Имя файла, удовлетворяющее маске ?*di . t?*, должно содержать один произвольный символ, стоящий в расширении файла после буквы t, следовательно, это имя может быть представлено в вариантах ответа 2, З и 4. Поэтому маске ?*di . t?* не удовлетворяет имя poydi . Е.
Номер ответа:
1.
Телекоммуникационные технологии
Инструменты создания информационных объектов
1. На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного ТР-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г. Восстановите 1Р-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем ИР-адресу.
|
|
|
|
|
|
|
|
в |
|
Решение
1Р-адресом является запись в виде четырех десятичных чисел от О до 255, разделенных точками.
Фрагмент А не может быть началом 1Р-адреса, поскольку он начинается с точки. Кроме того, данный фрагмент может занимать только последнее место в ТР-адресе — в противном случае одно из десятичных чисел 1Р-адреса было бы равно или 642, или 6416, или 648 (т. е. больше 255).
Фрагмент Г должен быть последним или после него должна стоять точка. Поскольку последнее место занимает фрагмент А, то фрагменту Г отводится третье место в 1Р-адресе.
Далее рассмотрим два возможных варианта — БВГА и ВБГА:
, БВГА — 2.16168.132.64; , ВБГА— 162.168.132.64.
Первый из этих вариантов нам не подходит, так как число 16168 больше 255.
Итак, у нас остается вариант, который и является решением задачи, — ВБГА.
Ответ: ВБГА.
2. Петя записал 1Р-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами 1Р-адреса. Эти фрагменты обозначе-
ны буквами А, Б, В и Г. Восстановите 1Р-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем 1Р-адресу.

Решение
1Р-адресом является запись в виде четырех десятичных чисел от О до 255, разделенных точками.
Фрагмент А не может быть началом 1Р-адреса, поскольку он начинается с точки. Кроме того, данный фрагмент может занимать только последнее место в 1Р-адресе — в противном случае одно из десятичных чисел 1Р-адреса было бы равно или 643, или 620 (т. е. больше 255).
Фрагмент Г должен быть последним или первым. Поскольку последнее место занимает фрагмент А, фрагменту Г отводится первое место в 1Р-адресе.
Второй из этих вариантов нам не подходит, так как число 1333 больше 255.
Итак, у нас остается вариант, который и является решением задачи, — ГБВА. ответ: ГБВА.
|
|
|
|
Б |
сот |
|
в |
. edu |
|
|
|
|
д |
.net |
|
Е |
htm |
|
Ж |
ftp |
З. Доступ к файлу htm. net, находящемуся на сервере сот . edu, осуществляется по протоколу ftp. В таблице фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет.
Решение
Имя ресурса всегда начинается с названия протокола — в данном случае это ftp. Кроме того, имя протокола должно отделяться от имени сервера знаками : / / . Далее следует имя сервера — сот.edu. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp : / / сот. edu/htm.net.
ответ: ЭКГБВАЕД.
|
|
.net |
|
Б |
ftp |
|
в |
|
|
|
|
|
|
|
|
Е |
.org |
|
Ж |
txt |
4. Доступ к файлу ftp . net, находящемуся на сервере txt . org, осуществляется по протоколу http. В таблице фрагменты адреса файла закодированы буквами от А до ЭК. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет .
Решение
Имя ресурса всегда начинается с названия протокола — в данном случае это http. Кроме того, имя протокола должно отделяться от имени сервера знаками : / /. Далее следует имя сервера — txt . org. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: http : / / txt.org /ftp . net.
Ответ: ГВЖЕДБА.
|
|
|
|
Б |
http |
|
|
|
|
|
. net |
|
|
|
|
|
|
|
Ж |
www |
5.
Решение
Имя ресурса всегда начинается с названия протокола — в данном случае это ftp. Кроме того, имя протокола должно отделяться от имени сервера знаками : / /. Далее следует имя сервера www . net. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp : / /www . net/ http . txt.
ответ: ВАЖГЕБД.
6. Идентификатор некоторого ресурса сети Интернет имеет следующий вид: http: / /www . ftp . ru/index . htm1. Какая часть этого идентификатора указывает на протокол, используемый для передачи ресурса?
Решение
Имя ресурса всегда начинается с названия протокола— в данном случае это http. ответ: НТТР.
|
а |
info |
|
Ь |
1ist |
|
с |
|
|
|
. doc |
|
|
ftp |
|
|
|
|
|
|
7. На сервере info . edu
находится файл 1ist . doc ![]() доступ к которому осуществляется по
протоколу ftp. Фрагменты адреса данного файла закодированы буквами а, Ь, с... g
(см. таблицу). Запишите последовательность этих букв, которая кодирует адрес
указанного файла в Интернете.
доступ к которому осуществляется по
протоколу ftp. Фрагменты адреса данного файла закодированы буквами а, Ь, с... g
(см. таблицу). Запишите последовательность этих букв, которая кодирует адрес
указанного файла в Интернете.
Решение
Имя ресурса всегда начинается с названия протокола — в данном случае это ftp. Кроме того, имя протокола должно отделяться от имени сервера знаками : / /. Далее следует имя сервера info . edu. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp : / /info . edu/list .doc.
|
А |
test |
|
Б |
demo |
|
в |
|
|
|
|
|
Д |
http |
|
Е |
. edu |
|
Ж |
. net |
Ответ: ecafgbd.
8.
Решение
Имя ресурса всегда начинается с названия протокола — в данном случае это http. Кроме того, имя протокола должно отделяться от имени сервера знаками : / /. Далее следует имя сервера test . edu. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp: // test . edu/demo . net.
Ответ: ДВАЕГБЖ.
|
а |
info |
|
|
|
|
с |
. net |
|
d |
. edu |
|
|
http |
|
f |
ехат |
|
|
|
9. На сервере info . edu находится файл ехат . net, доступ к которому осуществляется по протоколу http. Фрагменты адреса данного файла закодированы буквами а, Ь, с ... g (см. таблицу). Запишите последовательность этих букв, которая кодирует адрес указанного файла в Интернете.
Решение
Имя ресурса всегда начинается с названия протокола — в данном случае это http. Кроме того, имя протокола должно отделяться от имени сервера знаками : / / . Далее следует имя сервера info . edu.
После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp: //info. edu/exam. net.
Ответ: egadbfc.
|
|
|
|
Ь |
school |
|
с |
. net |
|
|
|
|
|
rating |
|
|
|
|
|
|
10. На сервере school . edu находится файл rating . net, доступ к которому осуществляется по протоколу ht tp. Фрагменты адреса данного файла закодированы буквами а, Ь, с... g (см. таблицу). Запишите последовательность этих букв, которая кодирует адрес указанного файла в Интернете.
Решение
Имя ресурса всегда начинается с названия протокола— в данном случае это http. Кроме того, имя протокола должно отделяться от имени сервера знаками : / /. Далее следует имя сервера sch001 . edu. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp : / / school . edu/rating.net.
Ответ: fgbadec.
|
|
. htm1 |
|
|
|
|
|
|
|
|
ftp |
|
д |
. ru |
|
Е |
http |
|
Ж |
index |
|
з |
|
11.
Решение
|
А |
news |
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
. edu |
|
|
|
Имя ресурса всегда начинается с названия протокола — в данном случае это http. Кроме того, имя протокола должно отделяться от имени сервера знаками : / /. Далее следует имя сервера www . ftp . ru. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp : / /www . ftp . ru/ index . html. ответ: ЕЗБГДВЖА.
12. На сервере news . edu находится файл 1ist . txt, доступ к которому осуществляется по протоколу ftp. Фрагменты адреса данного файла закодированы буквами А, В, С ... G (см. таблицу). Запишите последовательность этих букв, которая кодирует адрес указанного файла в Интернете.
Решение
Имя ресурса всегда начинается с названия протокола — в данном случае это ftp. Кроме того, имя протокола должно отделяться от имени сервера знаками : / /. Далее следует имя сервера news . edu. После имени сервера следует символ / , отделяющий его от имени файла. В результате имя ресурса будет следующим: ftp : / /news . edu/list . txt.
ответ: DGAFCEB.
13.

Решение
1Р-адресом является запись в виде четырех десятичных чисел от О до 255, разделенных точками.
Фрагмент Г не может быть началом 1Р-адреса, поскольку он начинается с точки. Кроме того, данный фрагмент может занимать только последнее место в 1Р-адресе — в противном случае одно из десятичных чисел 1Р-адреса было бы равно или 423, или 4221, или 422 (т. е. больше 255).
Фрагмент А должен быть последним или после него должна стоять точка. ПОСКОЛЬКУ последнее место занимает фрагмент Г, то фрагменту А отводится третье место в 1Р-адресе.
Далее рассмотрим два возможных
варианта — БВАГ и ВБАГ: , БВАГ — 212.123.212.42•, ![]()
![]() ВБАГ—
2.12213.212.42.
ВБАГ—
2.12213.212.42.
Второй из этих вариантов нам не подходит, так как число 12213 больше 255.
Итак, у нас остается вариант, который и является решением задачи, — БВАГ. ответ: БВАГ.
14. Петя записал 1Р-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами 1Р-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите 1Р-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем 1Р-адресу.

Решение
1Р-адресом является запись в виде четырех десятичных чисел от О до 255, разделенных точками.
Фрагмент В должен быть последним или после него должна стоять точка. Поскольку последнее место занимает фрагмент Б, фрагменту В отводится третье место в 1Р-адресе.
Далее рассмотрим два возможных
варианта — ГАВБ и АГВБ: , ГАВБ — 222.195.162.50•, ![]() АГВБ—
2.19225.162.50.
АГВБ—
2.19225.162.50.
Второй из этих вариантов нам не подходит, так как число 19115 больше 255.
Итак, у нас остается вариант, который и является решением задачи, — ГАВБ.
Ответ: ГАВЫ
15. Петя записал 1Р-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами ТР-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите 1Р-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем 1Р-адресу.

Решение
1Р-адресом является запись в виде четырех десятичных чисел от О до 255, разделенных точками.
Фрагмент В не может быть началом 1Р-адреса, поскольку он начинается с точки. Кроме того, данный фрагмент может занимать только последнее место в 1Р-адресе — в противном случае одно из десятичных чисел 1Р-адреса было бы равно или 733, или 7322, или 734 (т. е. больше 255).
Фрагмент А должен быть последним или после него должна стоять точка. Поскольку последнее место занимает фрагмент В, фрагменту А отводится третье место в 1Р-адресе.
Далее рассмотрим два возможных варианта БГАВ и ГБАВ:
, БГАВ — 224.133.133.73;
![]() ГБАВ — 4.13223.133.73.
ГБАВ — 4.13223.133.73.
Второй из этих вариантов нам не подходит, так как число 13223 больше 255.
Итак, у нас остается вариант, который и является решением задачи, — БГАВ.
16. Петя записал 1Р-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами 1Р-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите 1Р-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем 1Р-адресу.

Решение
1Р-адресом является запись в виде четырех десятичных чисел от О до 255, разделенных точками.
Фрагмент В не может быть началом 1Р-адреса, поскольку он начинается с точки. Кроме того, данный фрагмент может занимать только последнее место в 1Р-адресе — в противном случае одно из десятичных чисел 1Р-адреса было бы равно или 643, или 6418 (т. е. больше 255).
Фрагмент А должен быть последним или после него должна стоять точка. Поскольку последнее место занимает фрагмент В, фрагменту А отводится третье место в 1Р-адресе.
Далее рассмотрим два возможных варианта ГБАВ и БГАВ:
, ГБАВ — 183.253.231.64;
Второй из этих вариантов нам не подходит, так как число 25183 больше 255.
Итак, у нас остается вариант, который и является решением задачи, — ГБАВ.
Ответ: ГБАВ.
Литература
1. Андреева Е. В., Босова Л. Л., Фалина И. Н. Математические основы информатики. Элективный курс: Учебное пособие. 2-е изд.. испр. М.: БИНОМ. Лаборатория знаний, 2007.
2. Бешенков С. А., Ракитина Е. А. Информатика. Систематический курс. Учебник для 10 класса. 2-е изд. М.: БИНОМ. Лаборатория знаний, 2006.
З. Бешенков С. А., Кузьмина Н. В., Ракитина Е. А. Информатика. Систематический курс. Учебник для 11 класса. 2-е изд. М.: БИНОМ. Лаборатория знаний, 2007.
4. Горячев А. В., Шафрин Ю. А. Практикум по информационным технологиям. М.: Лаборатория Базовых Знаний, 1999.
5. Демонстрационные варианты ЕГЭ. Центр интенсивных технологий образования [электронный ресурс]. URL: http://www. gotovkege. ru
6. Единый государственный экзамен 2007. Информатика. Учебнотренировочные материалы для подготовки учащихся / ФИПИ, авторы-составители: П. А. Якушкин, С. С.Крылов, В. Р. Лещинер. М.: Интеллект-Центр, 2007.
7. ЕГЭ-2009. Информатика: сборник экзаменационных заданий. Федеральный банк экзаменационных материалов/ ФИПИ, авторысоставители: П. А. Якушкин, С. С. Крылов. М.: Эксмо, 2009.
8. Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся / ФИПИ, авторы-составители: Якушкин П. А., Крылов С. С., Лещинер В. Р. М.: Интеллект-Центр, 2009.
9. Единый государственный экзамен: Информатика: Контрольные измерительные материалы: Репетиционная сессия. / П. А. Якушкин. М.: Вентана-Граф, 2007.
10. ЕГЭ. Информатика: Раздаточный материал тренировочных тестов» / Гусева И.Ю. СПб.: Тригон, 2008.
11. Единый государственный экзамен. Открытый сегмент ФБТЗ. Информатика [электронный ресурс]. URL: http://www.fipi.ru/view/ sections/160/docs/
12. Залогова Л. А. Практикум по компьютерной графике. М.: Лаборатория Базовых Знаний, 2001.
13. Заславская О. Ю., Левченко И. В. Информатика и информационнокоммуникационные технологии. Справочные материалы: Учебное пособие для учащихся средних школ и абитуриентов педагогических вузов. М.: АПКиППРО, 2005.
Литература
![]()
14. Заславсњая О. Ю., Левченко И. В. Информатика и информационнокоммуникационные технологии. Экзаменационные задачи, вопросы и тестовые задания. М.: МГПУ, 2006.
15. Заславская О. Ю., Левченко И. В. Теоретический материал для подготовки к вступительным испытаниям по информатике и ИКТ. Изд-е 2, перераб. и доп. М.: мгпУ, 2007.
16. Информатика. 7—9 класс / Под ред. Н. В. Макаровой. СПб. : Питер, 2003.
17. Информатика. 10—11 класс / Под ред. Н. В. Макаровой. СПб. : Питер, 2002.
18. Информатика. Задачник-практикум в 2 т. /Под ред. И. Г. Семакина и Е. К. Хеннера. М.: Лаборатория Базовых Знаний, 1999.
19. Контрольно-измерительные материалы. [электронный ресурс]. URL: http://www.fipi.ru/view/sections/92/docs/
20. Кузнецов А. А. Информатика. Тестовые задания. / Кузнецов А. А., Пугач В. И., Добудько Т. В., Матвеева Н. В. 3-е изд. М.: БИНОМ. Лаборатория знаний, 2006.
21. Левченко И. В., Заславская О. Ю. Информатика и информационнокоммуникационные технологии. Сборник учебных задач. Часть 1. М.: АПКиППРО, 2006.
22. Левченко И. В., Заславская О. Ю. Информатика и информационно-коммуникационные технологии. Ответы к учебным задачам. Часть П. М.: АПКиППРО, 2006.
23. Левченко И. В., Заславская О. Ю. Конкретизация требований к результатам обучения информатике и информационно-коммуникационным технологиям выпускников школ. Вестник МГПУ. Серия «Информатика и информатизация образования» . 2004. №2(3).
24. Левченко И. В., Заславская О. Ю. Система задач для овладения учащимися основной школы содержательным и алфавитным подходом к измерению информации / / Информатика и образование. 2006. Г.Г211, 12.
25. Лыскова В. Ю., Ракитина Е. А. Логика в информатике. М.: БИНОМ. Лаборатория знаний, 2006.
26. Могилев А. В., Пак Н. И., Хеннер Е. К. Практикум по информатике. М.: ACADEMIA, 2001.
27. Самылкина Н. Н, Русаков С. В., Шестаков А. П., БаДанина С. В. Готовимся к ЕГЭ по информатике. Элективный курс: учебное пособие. 3-е изд. М.: БИНОМ. Лаборатория знаний, 2009.
28. Самылкина
Н. Н, Калинин И. А., Левченко И. В. Методические рекомендации по использованию
плакатов «Информатика и ИКТ. Основная школа»: Учебно-методическое пособие. М.:
БИНОМ. Лаборатория знаний, 2005. ![]()
29. Самылкина Н. Н. Построение тестовых заданий по информатике. 2-е изд., испр. и доп. М.: БИНОМ. Лаборатория знаний, 2006.
360 Литература
![]()
30. Семакин И. Г. и др. Информатика. Учебник по базовому курсу. М.: Лаборатория Базовых Знаний, 1998.
31. Семакин И. Г., Вараксин Г. С. Информатика. Структурированный конспект базового курса. М.: Лаборатория Базовых Знаний, 2001.
32. Семакин И. Г., Хеннер Е. К. Информатика. 10 класс. М.: Лаборатория Базовых Знаний, 2001.
33. Семакин И. Г., Хеннер Е. К. Информатика. 11 класс. М.: Лаборатория Базовых Знаний, 2002,
34. Угринович Н. Д. Информатика и информационные технологии. Учебное пособие для 10—11 классов. М.: Лаборатория Базовых Знаний, 2001.
35. Угринович Н. Д., Босова Л. Л., Михайлова Н. И. Практикум по информатике и информационным технологиям. Учебное пособие для 10—11 классов. М.: Лаборатория Базовых Знаний, 2001.
36. Шафрин Ю. А. Информационные технологии: В 2 ч. М.: Лаборатория Базовых Знаний, 1999.
37. Шауцукова Л. З. Информатика: Учебное пособие для 10—11 кл. общеобразоват. учреждений. М.: Просвещение, 2000.
[1] . Скорость передачи данных через ![]() равна 128 ООО бит/с. Через данное соединение
передают файл размером 625 Кбайт. Определите время передачи этого файла в секундах.
равна 128 ООО бит/с. Через данное соединение
передают файл размером 625 Кбайт. Определите время передачи этого файла в секундах.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.