
Данная работа представляет собой подробный разбор различных типов задач по теме «Решение уравнений и их систем», предлагаемых на ОГЭ в качестве задания №21. Этот разбор подразумевает подробное решение и методические комментарии.
Можно встретить множество разнообразных заданий по данной теме. Наиболее простым и доступным для восприятия учащимися является следующее:
1) Решить уравнение ![]() .
.
Решение с методическими комментариями Перенеся все слагаемые в левую часть уравнения, получим:
![]()
Квадратные корни в силу противоположности уничтожаются, остаётся квадратное уравнение:
𝑥2 − 5𝑥 + 4 = 0,
корнями которого являются числа 1 и 4. Принципиальный момент: корень 𝑥 = 4 является посторонним, так как при подстановке его в первоначальное уравнение получим квадратный корень из отрицательного числа, чего быть не должно. Корень 𝑥 = 1 подходит, в чём убеждаемся непосредственной проверкой.
Заметим, что эта математическая ловушка срабатывает практически всегда – учащиеся записывают в ответ оба корня, что приводит к потере половины баллов на ОГЭ. Преодолеть эту трудность можно двумя стандартными путями:
1) сразу найти ОДЗ неизвестной 𝑥 (в данном случае имеем 𝑥 ≤ 3). Отыскав корни, проверяем, входят ли они в найденный промежуток;
2) осуществить проверку, подставив найденные корни в первоначальное уравнение. Слово «первоначальное» является ключевым, так как, подставив найденные корни в преобразованное (квадратное) уравнение, учащийся не сможет установить тот факт, что один из корней является посторонним. Отметим, что учащиеся должны понимать следующий факт: такие преобразования уравнения как сокращение дробей и приведение подобных слагаемых могут привести (не всегда) к расширению ОДЗ неизвестной. Поэтому нужно действовать одним из двух способов, о которых говорилось выше.
Ответ: 𝑥 = 1.
2) Решить уравнение (𝑥 − 3)4 − 3(𝑥 − 3)2 = 10.
С точки зрения рационального подхода, самой грубой ошибкой является раскрытие скобок и приведение подобных слагаемых. Во-первых, не все образовательные программы по математике предусматривают изучение темы «Бином Ньютона», поэтому учащиеся не могут возвести разность в четвёртую степень. Во-вторых, даже при успешном раскрытии скобок и последующих верных преобразованиях ученик получит общее уравнение четвёртой степени, методы решения которого в школе не изучаются.
В этой связи можно заметить, что четвёртая степень — это квадрат квадрата, поэтому уравнение можно переписать так:
((𝑥 − 3)2)2 − 3(𝑥 − 3)2 = 10.
Видим, что выражение (𝑥 − 3)2 повторяется дважды, причём больше неизвестная нигде не встречается. Следовательно, можно выполнить замену (𝑥 − 3)2 = 𝑡. Тогда уравнение примет вид:
𝑡2 − 3𝑡 = 10.
Перенеся все слагаемые влево, получим квадратное уравнение, корнями которого являются числа 5 и −2. Выписывание этих двух чисел в ответ – одна из распространённых ошибок; учащиеся забывают о том, что найдены значения неизвестной 𝑡, а не 𝑥. Поэтому следующим этапом решения является возвращение к неизвестной 𝑥. Необходимо вспомнить, какое выражение обозначалось буквой 𝑡, и это выражение приравнять к 5 (первый случай) и к −2 (второй случай).
1 случай. (𝑥 − 3)2 = 5. Это уравнение можно решить двумя способами:
![]()
1) если квадрат величины равен 5, то сама эта величина равна либо √5, либо −√5. Тогда либо
![]()
𝑥 − 3 = √5 ⇒ 𝑥 = 3 + √5, либо 𝑥 − 3 = −√5 ⇒ 𝑥 = 3 − √5.
2) возвести левую часть в квадрат, перенести всё влево и решить полученное квадратное уравнение.
2 случай. (𝑥 − 3)2 = −2. Это уравнение не имеет действительных корней, так как квадрат любой величины неотрицателен.
![]()
![]() Ответ:
𝑥 = 3 + √5,
𝑥 = 3 − √5.
Ответ:
𝑥 = 3 + √5,
𝑥 = 3 − √5.
3) Решить уравнение (𝑥2 − 25)2 + (𝑥2 + 3𝑥 − 10)2 = 0.
Очевидно, что возведение в квадрат приведёт к громоздким преобразованиям (в обязательной программе по математике отсутствует формула (𝑎 + 𝑏 − 𝑐)2; кроме этого, ученики не готовы к решению общего уравнения четвёртой степени). Учащиеся должны вспомнить тот факт, что квадрат любого число неотрицателен. Далее учитель подчёркивает специфическую структуру уравнения – сумма квадратов двух величин равна нулю. Такое возможно только в том случае, когда обе величины (одновременно) равны нулю. Так как это выполняется одновременно, получим систему уравнений:
![]() .
.
Оба уравнения решают стандартно (первое – неполное квадратное, второе – полное квадратное). Корни первого уравнения: −5 и 5. Корни второго уравнения: −5 и 2. Решением системы является число −5 (так как оно является корнем и первого уравнения, и второго).
Замечание: первое уравнение системы целесообразно решать путём разложения левой части на множители (по формуле разности квадратов):
(𝑥 + 5)(𝑥 − 5) = 0.
Выбор этого способа обусловлен тем, что, решая уравнение путём приведения к виду
𝑥2 = 25,
подавляющее большинство учащихся записывает только один ответ, а именно число 5, то есть отрицательный корень уравнения упускается. Видим, что первый путь решения автоматически исключает такую ошибку.
Ответ: 𝑥 = −5.
4) Решить уравнение 𝑥4 = (𝑥 − 2)2.
По ранее указанным причинам выполнять возведение в квадрат и преобразовывать полученное уравнение нецелесообразно. Здесь опять следует заметить, что четвёртую степень можно рассматривать как квадрат квадрата. Затем применяется формула разности квадратов. Имеем:
𝑥4 = (𝑥 − 2)2;
(𝑥2)2 = (𝑥 − 2)2;
(𝑥2)2 − (𝑥 − 2)2 = 0; (𝑥2 + (𝑥 − 2))(𝑥2 − (𝑥 − 2)) = 0;
(𝑥2 + 𝑥 − 2)(𝑥2 − 𝑥 + 2) = 0.
Произведение равно нулю только в том случае, когда хотя бы один из множителей равен нулю. Поэтому имеет место совокупность (полезно напомнить ученикам, что система это «И», а совокупность это «ИЛИ»):
![]() ,
,
Второе уравнение не имеет действительных корней (в силу отрицательности дискриминанта), корнями первого уравнения являются числа −2 и 1.
Этот способ наиболее стандартный. Однако сильным учащимся можно предложить и другие подходы к решению.
Второй способ решения. Приведя уравнение к
виду ![]() , учитель замечает его структуру – квадрат
одной величины равен квадрату другой величины. Натолкнуть учащихся на идею
решения можно, задав вопрос: «В каком случае квадраты двух величин совпадают?»
(когда эти две величины либо равны, либо противоположны). Отсюда получается
совокупность:
, учитель замечает его структуру – квадрат
одной величины равен квадрату другой величины. Натолкнуть учащихся на идею
решения можно, задав вопрос: «В каком случае квадраты двух величин совпадают?»
(когда эти две величины либо равны, либо противоположны). Отсюда получается
совокупность:
![]() .
.
Дальнейший ход решения очевиден.
Третий способ решения. Опять приведём
исходное уравнение к виду ![]() . Две неотрицательные
величины равны, а, следовательно, квадратные корни из этих величин тоже равны.
Поэтому, извлекая из обеих частей уравнения квадратный корень, получим:
. Две неотрицательные
величины равны, а, следовательно, квадратные корни из этих величин тоже равны.
Поэтому, извлекая из обеих частей уравнения квадратный корень, получим: ![]() .
.
Снова получается совокупность (точнее, совокупность систем):
![]() .
.
Решив квадратное уравнение (и одно, и другое), необходимо отобрать корни (т.е, выбрать тот (те), который(е) входит(ют) в заданный промежуток).
Ответ:
![]() .
.
5) Решить уравнение ![]()
Решение с методическими комментариями Заметим, что данное уравнение можно решить по алгоритму, стандартному для дробнорациональных уравнений – в данном случае излишне громоздких преобразований не получится.
Однако, переписав уравнение в виде
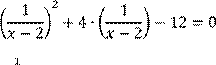 ,
,
можно заметить, что выражение ![]() повторяется дважды, и
неизвестная больше в уравнении не встречается. Значит, можно провести замену
повторяется дважды, и
неизвестная больше в уравнении не встречается. Значит, можно провести замену
![]() .
.
В таком случае уравнение примет вид
![]() .
.
Корнями этого уравнения являются числа ![]() и
и ![]() .
Теперь следует вернуться к неизвестной
.
Теперь следует вернуться к неизвестной ![]() (получим совокупность):
(получим совокупность):
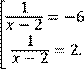 ,
,
Решив эту совокупность, найдём значения неизвестной 𝑥.
Замечание: многие учащиеся используют замену 𝑥 − 2 = 𝑡.
Эта замена действительно имеет место, но, используя её, не удастся избавиться от дробей. В итоге (после надлежащих преобразований) получится дробно-рациональное уравнение. В этой связи стоит полагать, что предложенная выше замена гораздо более рациональна, хотя усмотреть её несколько труднее.
Ответ:
![]() .
.
![]() ,
,
6) Решить систему уравнений
Это система уравнений второй степени, решение которой выполняется по стандартному алгоритму. В данном случае удобен способ подстановки, так как неизвестная 𝑦 уже выражена через неизвестную 𝑥. Подставив (в первое уравнение) вместо неизвестной 𝑦 выражение 2𝑥 − 1, перенеся всё в левую часть и приведя подобные слагаемые, получим квадратное уравнение:
2𝑥2 − 3𝑥 + 1 = 0.
Корнями этого уравнения являются числа 1 и 0,5. Отыскав значения неизвестной 𝑥, можно найти соответствующие значения неизвестной 𝑦. Для этого подставим в любое уравнение (например, во второе) вместо неизвестной 𝑥 соответствующие значения. Получим два решения системы: (1; 1), (0,5; 0).
Замечание: 1) Способ сложения для решения данной системы, очевидно, нецелесообразен, но также имеет место быть; 2) Можно рассуждать и по-другому. Так как правые части двух равенств совпадают, то и левые части тоже совпадут. Дальнейшее решение полностью повторяет вышеприведённое.
Ответ: (1; 1), (0,5; 0).
![]() 7) Решить систему
уравнений
7) Решить систему
уравнений
.
Сначала желательно обратить внимание учащихся на левые части уравнений, а именно, на пропорциональность коэффициентов. Можно заметить, что, домножая обе части первого уравнения на 2, получим систему:
![]() .
.
Таким образом, левые части двух равенств совпали. Следовательно, должны совпасть и правые части. Получим уравнение 24𝑥 = 48, откуда легко найти 𝑥 = 2. Отыскав значение неизвестной 𝑥, можно найти соответствующие значения неизвестной 𝑦. Для этого подставим в любое уравнение (например, в первое) вместо неизвестной 𝑥 соответствующее значение. Получим два решения системы: (2; 2), (2; −2).
Замечание: 1) строго говоря, в данной системе можно использовать и способ подстановки (выражать при этом придётся не неизвестную, а её квадрат), но это абсолютно не рационально, так как повлечёт ряд преобразованй.
2) стоит также оговорить весьма популярную ошибку многих учеников. Это ошибка, вызванная непониманием смысла фразы «выразить одну неизвестную через другую». Заключается она в том, что одна и та же неизвестная встречается и в левой части равенства, и в правой. Например, дано равенство 𝑥 + 2𝑦 = 3 − 2𝑥. Из него следует выразить одну из букв. Наиболее частый неправильный ответ: 𝑥 = 3 − 2𝑥 − 2𝑦. Первое условие (в левой части неизвестная в первой степени и с коэффициентом 1) выполнено, а второе (ключевое – в правой части эта неизвестная отсутствует) – нет.
Ответ: (2; 2), (2; −2).
1 вариант Решить уравнение:
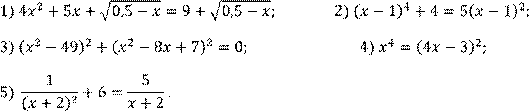
Решить систему уравнений:
![]() 6)
6)
.
Решить уравнение:
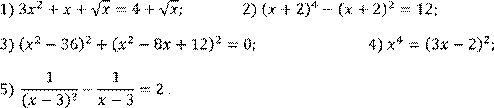
Решить систему уравнений:
![]() 6)
6)
.
3 вариант Решить уравнение:
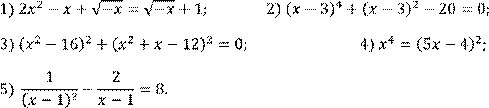
Решить систему уравнений:
![]() 6)
6)
.
4 вариант Решить уравнение:
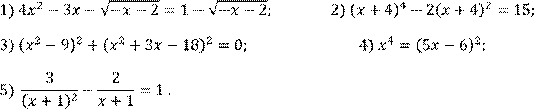
Решить систему уравнений:
![]() 6)
6)
.
5 вариант Решить уравнение:
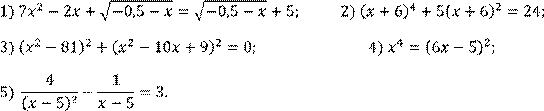
Решить систему уравнений:
![]() 6)
6)
.
Решить уравнение:
![]()
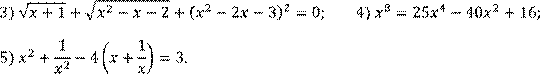
Решить систему уравнений:
![]() ,
,
6)
|
Номер задания |
|
|
Ответ |
|
|
|
|
1 вариант
|
2 вариант |
3 вариант |
4 вариант |
5 вариант |
6 вариант |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
(1;1), (1;-1) |
(2;1), (-2;1) |
(2;2), (-2;2) |
(3;1), (-3;1) |
(1;-3), (-1;-3) |
(2;1), (-1;-2) |
1) Алгебра. 9 класс: учеб. для общеобразовательных учреждений / под ред. С.А. Теляковского. – М.: Просвещение, 2011. – 271 с.: ил.
2) ОГЭ 2018. Математика. 50 вариантов. Типовые тестовые задания от разработчиков ОГЭ / под ред. И.В. Ященко – М.: Экзамен, 2018. -303 с.
3) Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы: 9 класс/ Л.В. Кузнецова и др. – М.: Дрофа, 1996. – 144 с.: ил.
4) Я сдам ОГЭ! Модульный курс. Математика. Практикум и диагностика. / И.В. Ященко, С.А. Шестаков. – М.: Просвещение, 2017, -287 с.: ил.
5) http://fipi.ru/
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.