
Цель работы: ознакомление с методами решения задач линейного программирования в табличном процессоре Excel.
Решение экономических задач, как правило, связано с необходимостью учета разнообразных факторов и характеристик (параметров), которые влияют друг на друга и на экономические процессы. С этой целью проблемы экономики исследуют на адекватных математических моделях и далее применяют методы оптимизации в соответствии с выбранными критериями. Большое число экономических задач сводится к линейным математическим проблемам, которые традиционно называют моделями линейного программирования. Аппарат линейного программирования широко используется для анализа возможностей экономических систем и принятия обоснованных решений об их развитии.
Использование информационных технологий для решения задач линейного программирования – актуальное и перспективное направление как для специалистов, занимающихся менеджментом и маркетингом, так и для всех тех, кто по роду своей деятельности связан с решением задач оптимизации.
В настоящей работе кратко рассматриваются теоретические аспекты задач линейного программирования, а также практические приемы их решения на примерах конкретных экономических задач средствами табличного процессора Excel 2000.
В общем виде задача линейного программирования ставится следующим образом:
Найти максимум (минимум) целевой функции
n
|
F =∑c j x j j=1 при ограничениях |
(2.1) |
|
n ∑aij x j ≤ bi ,(i =1,...,m1) j=1 ∑n aij x j = bi ,(i = m1 +1,...,m) |
(2.2) |
j=1
x j ≥ 0,( j =1,...,n),
где xj – (управляющие) переменные, bi , aij – параметры, F – целевая функция.
Функция (2.1) – линейная, ограничения (2.2) – линейные. Задача содержит n переменных и m ограничений.
Решить задачу линейного программирования – это значит найти такие значения управляющих переменных xj , которые удовлетворяют ограничениям (2.2) и при которых целевая функция (2.1) принимает наибольшее (наименьшее) значение. Для решения задач линейного программирования обычно используют симплекс-метод.
Для использования симплекс-метода задачу необходимо записать в канонической форме – целевая функция должна достигать максимума, ограничения, налагаемые на переменные, должны быть равенствами, а сами переменные неотрицательными:
a11x1 + a12x2 + ...+ a1n xn = b1 a21x1 + a22x2 + ...+ a2n xn = b2
...... (2.4)
xij ≥ 0, j =1,...n
Симплекс-метод представляет собой направленный перебор решений системы (2.3) – (2.4), при этом каждое следующее решение улучшает (увеличивает) значение целевой функции.
В качестве иллюстрации рассмотрим решение задачи планирования производства продукции в условиях наличия ограничений на ресурсы. Пусть требуется определить, в каком количестве необходимо выпускать продукцию четырех типов Прод1, Прод2, Прод.3 и Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырьевые и финансы. Норма расхода, а также прибыль, получаемая от реализации каждого вида продукции, приведены в табл. 2.1:
Таблица 2.1
|
Ресурс |
Прод1 |
Прод2 |
Прод3 |
Прод4 |
Знак |
Наличие |
|
Прибыль |
60 |
70 |
120 |
130 |
max |
|
|
Трудовые |
1 |
1 |
1 |
1 |
≤ |
16 |
|
Сырье |
6 |
5 |
4 |
3 |
≤ |
110 |
|
Финансы |
4 |
6 |
10 |
13 |
≤ |
100 |
Данная задача относится к типу задач, которые называют задачами планирования производства. Пусть x1, x2, x3, x4 - количество каждого из четырех видов продукции; Z – целевая функция, которая представляет собой прибыль от реализации произведенной продукции. Математическая модель задачи может быть представлена следующим образом:
Z = 60 x1 + 70 x 2+ 120 x3 + 130 x4 → max (2.5)
x1 + x2 + x3 + x4 ≤16 6x1 + 5x2 + 4x3 + 3x4 ≤110
(2.6)
4x1 + 6x2 +10x3 +13x4 ≤100
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
Решение задачи будем производить в следующей последовательности:
1. В Excel на Листе 1 создайте форму и введите в нее исходные данные задачи (рис. 2.1 ).
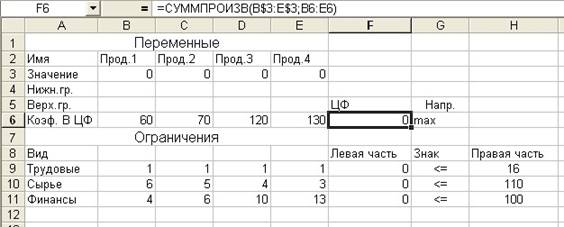
Рис. 2.1
2. Введите зависимость для целевой функции: установите курсор в ячейку F6 и вызовите Мастер функций. В списке математических функций выберите функцию СУММПРОИЗВ, в массив1 введите B$3:E$3, в массив2 введите B6:E6.
3. Введите зависимость для левых ограничений. Для этого скопируйте формулу из ячейки F6 в ячейки F9, F10 и F11, используя специальную вставку.
4. Установите курсор в ячейку F6 и выполните команду Сервис – Поиск решения.
5. Введите направление целевой функции: Максимальному значению.
6. Введите адреса искомых переменных – установите курсор в поле Изменяя ячейки и введите $B$3:$E$3.
7. Нажмите кнопку Добавить. На экране появится диалоговое окно Добавление ограничения. Введите граничные условия на переменные:
$B$3>=$B$4, $C$3>=$C$4, $D$3>=$D$4, $E$3>=$E$4, $F$9<=$H$9, $F$10<=$H$10, $F$11<=$H$11 (см. рис. 2.1). После ввода последнего ограничения в диалоговом окне Добавление ограничения вместо Добавить нажмите кнопку OK. Если при вводе задачи возникает необходимость в изменении или удалении уже введенных ограничений, то это можно сделать с помощью кнопки Изменить или Удалить.
8. Нажмите кнопку Параметры диалогового окна Поиск решения. С помощью команд, включенных в это диалоговое окно, можно вводить условия для решения задач оптимизации всех классов. Команды, используемые по умолчанию, подходят для решения большей части практических задач. Команда Максимальное время служит для назначения времени в секундах, выделяемого на поиск решения задачи (не более 32767 секунд = 9 часов).
9. Установите опцию Линейная модель и Неотрицательные значения, что будет означать применение симплекс-метода. Нажмите кнопку OK.
10. Нажмите кнопку Выполнить. На экране появится диалоговое окно Результаты поиска решений. Тем самым мы найдем решение задачи, если таковое существует. В противном случае, если условия задачи несовместны, будет получена информация о том, что Поиск не может найти подходящего решения.
Для нашего примера мы получаем, что целевая функция принимает максимум, равный 1320 ед. при x1 =10, x2 = 0, x3 = 6, x4 = 0. Правые части ограничений соответственно принимают значения, равные 16, 84 и 100.
Анализ оптимального решения начинается после успешного решения задачи, когда на экране появляется диалоговое окно Результаты поиска решения с сообщением Решение найдено. С помощью этого диалогового окна можно вызвать отчеты трех типов: результаты, устойчивость, пределы.
Рассмотрим, например, как формируется отчет по результатам. Для этого перейдем на Лист1 и выполним команду Сервис – Поиск решения – Выполнить. Выберем тип отчета – Результаты и нажмем кнопку OK. Отчет по результатам состоит из таблицы, в которой приводятся сведения о целевой функции, о значениях искомых переменных, полученных в результате решения задачи; о количестве неиспользованных ресурсов и о статусе переменных (связанное/несвязанное).
Аналогичным образом можно вызвать и другие два вида отчетов – устойчивость и пределы.
Под параметрическим анализом задачи будем понимать решение задачи оптимизации при различных значениях того параметра (параметров), который ограничивает улучшение (возрастание в задаче на максимум) целевой функции. С этой целью проанализируем в только что рассмотренном примере, как будет изменяться оптимальное значение целевой функции например при изменении значений имеющихся в распоряжении финансов:
|
Финансы |
50 |
100 |
150 |
200 |
250 |
1. Скопируйте Лист1 ,присвоив ему имя Параметрический анализ, удалите результат решения, находящийся в B3:E3.
2. Решите задачу для первого значения финансов (50), выполнив команду
Сервис - Поиск решения – Выполнить; на экране появится диалоговое окно
Результаты поиска решения. Нажмите кнопку Сохранить сценарий. Введите имя сценария – Финансы = 50 и нажмите кнопку OK. На экране снова откроется диалоговое окно Результаты поиска решений, где надо также нажать кнопку OK. Аналогично нужно решить задачу для всех других значений выбранного параметра, присваивая каждому соответствующее имя сценария. Не забывайте перед каждым решением задачи с новым значением параметра удалять предыдущий результат решения!
С помощью «Диспетчера сценариев» восстановим все полученные результаты. Для этого выполним команду Сервис – Сценарии – добавить (адреса изменяемых ячеек) – структура и т. д., следуя подсказкам. Результатом будет таблица, приведенная ниже.
Для наглядного представления результатов параметрического анализа на основании полученных данных построим соответствующие графики. Например, можно построить график, на котором будет видно, что при различном финансировании в план входит продукция различных видов, однако ни в один вариант не войдет выпуск продукции Прод 2 (Рис. 2.2). Это можно объяснить тем, что при высоком потреблении ресурсов прибыль от ее производства ниже, чем от производства других видов продукции. На рис. 2.3 отражено изменение прибыли в зависимости от значений выбранного параметра, а на рис. 2.4 - зависимость использованного сырья от финансов.
|
|
ф=50 |
ф=100 |
ф=150 |
ф=200 |
ф=250 |
|
Пр1 |
12,50 |
10,00 |
1,67 |
0,00 |
0,00 |
|
Пр2 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
Пр3 |
0,00 |
6,00 |
14,33 |
2,67 |
0,00 |
|
пр4 |
0,00 |
0,00 |
0,00 |
13,33 |
16,00 |
|
прибыль |
750,00 |
1320,00 |
1820,00 |
2053,33 |
2080,00 |
|
труд. |
13,00 |
16,00 |
16,00 |
16,00 |
16,00 |
|
сырье |
75,00 |
84,00 |
67,00 |
50,67 |
48,00 |
|
финансы |
50,00 |
100,0 |
150,00 Рис.2.2 |
200,00 |
208,00 |

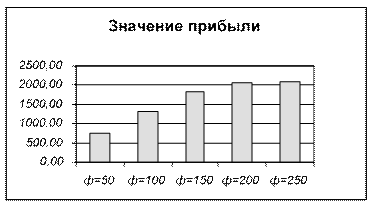
Рис.2.3
|
Зависимость использованного сырья от финансов
250,00 |
|
|
|
|
|
|
|
Рис.2.4
Допустим, что ваша фирма занимается переработкой сельскохозяйственной продукции на нескольких заводах, расположенных в разных районах Москвы. Сырье поставляется объединениями производителей со складов, расположенных в различных городах Московской области. Стоимость сырья не зависит от того, где оно произведено, однако перевозка со склада на завод зависит от расстояния и различна для каждого склад и завода. Тарифы на перевозку одной тонны груза известны и могут быть представлены в виде матрицы стоимостей
|
(сij): |
47,00 39,00 23,65 19,50 39,00 |
41,50 32,30 27,30 19,40 36,00 |
45,00 38,00 21,00 9,00 27,50 |
32,65 41,00 18,00 24,00 44,00 |
(2.9) |
Потребности заводов в сырье (bj) различны и запасы на каждом складе (ai) ограничены:
|
ai \ bj |
240 |
115 |
280 |
370 |
|
300 |
|
|
|
|
|
240 |
|
|
|
|
|
170 |
|
|
|
|
|
120 |
|
|
|
|
|
320 |
|
|
|
|
Требуется составить план перевозок так, чтобы их общая стоимость была минимальна.
Прежде всего, как всегда, необходимо построить математическую модель задачи. Цель задачи состоит в минимизации суммарной стоимости всех перевозок, что может быть достигнуто с помощью оптимальной организации доставки грузов. Следовательно, в качестве переменных нужно взять xij - количество тонн сырья, перевозимого от i - го поставщика j - му потребителю; cij - коэффициенты матрицы стоимостей (2.9). Параметры задачи – число поставщиков и потребителей, предложения и спрос сырья в каждом пункте, тарифы на перевозки.
Ограничения задачи – это ограничения на предложение и спрос сырья: запасы сырья у поставщиков ограничены, с одной стороны, а с другой стороны, запросы производителей должны быть удовлетворены. Целевая функция представляет собой суммарные затраты S на перевозку сельхозпродукции, равные сумме произведений тарифов на перевозку на количество перевозимого сырья от каждого поставщика каждому потребителю.
Итак, математическая модель транспортной задачи будет выглядеть следующим образом.
Целевая функция:
c11x11 + c12x12 + c13x13 + c14x14 + c21x21 + c22x22 + c23x23 + c24x24 +
Z(X) = c31x31 + c32x32 + c33x33 + c34x34 + (2.10)
c41x41 + c42x42 + c43x43 + c44x44 + c51x51 + c52x52 + c53x53 + c54x54 → min Ограничения задачи:
x11 + x12 + x13 + x14 ≤ 300
x21 + x22 + x23 + x24 ≤ 240
x31 + x32 + x33 + x34 ≤170
x41 + x42 + x43 + x44 ≤120
x51 + x52 + x53 + x54 ≤ 320
x11 + x21 + x31 + x41 + x51 = 240 (2.11)
x12 + x22 + x32 + x42 + x52 =115
x13 + x23 + x33 + x43 + x53 = 280 x14 + x24 + x34 + x44 + x54 = 370
xij ≥ 0
Целевая функция и ограничения линейны, поэтому данная задача относится к задачам линейного программирования и может быть решена с помощью симплекс-метода. Следует заметить, что благодаря особой структуре такие задачи носят название транспортных задач, и для их решения применяют с успехом также так называемый метод потенциалов. Мы же будем решать ее подобно тому, как решали задачи на планирование производства.
Создайте на листе Транспортная задача таблицу, представленную на
рис.2.7
Рис. 2.7 Исходные данные транспортной задачи
В ячейке B4 находится формула =СУММ(C4:F4); скопируйте содержимое ячейки B4 в ячейки B5:B8. Массив ячеек C4:F8 заполнен единицами в качестве начального плана перевозок; установите числовой формат для этих ячеек. В ячейку C9 введите формулу = СУММ(C4:C8). Скопируйте формулу в ячейки D9:F9.
Первая часть таблицы подготовлена. Каждое значение в ячейках, находящихся на пересечении столбца какого-либо завода и строки склада обозначает количество тонн сырья, поставляемого в месяц с этого склада на данный завод. В нижней строке суммируются общее количество сырья, поставляемого на определенный завод, во втором столбце – общее количество закупленного у конкретного склада сырья.
Далее введите требуемые объемы поставок и цены поставок. Скопируйте названия складов в ячейки с A11 по A15. В ячейки B11:B15 занесите объемы месячных запасов сырья на различных складах; в ячейки C11:F15 занесите стоимости перевозки тонны сырья с конкретного склада на конкретный завод. В ячейку С16 введите формулу = =C4*C11+C5*C12+C6*C13+C7*C14+C8*C15, которая вычисляет полную стоимость перевозок сырья на первый завод. Скопируйте формулу из ячейки С16 в ячейки D16:F16. В ячейку B16 введите формулу = СУММ(C16:F16). В данной ячейке будет вычисляться общая стоимость перевозки сырья. Выполните поиск решения (Сервис – Поиск решения) с целью определения минимальных затрат на перевозки при соблюдении всех заданных условий:
• Объем поставок с конкретного склада должен быть меньше или равен запасам на складе;
• Объем перевозок не должен быть отрицательным;
• Запросы заводов должны быть выполнены полностью. Перевыполнение поставок допустимо, а недовыполнение – нет. Значения полей диалогового окна Поиск решения выглядят следующим образом:
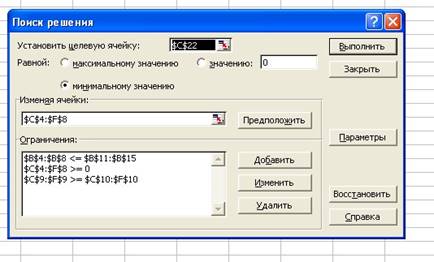
Обратите внимание: целевая ячейка – B16!
Сохраните результаты поиска решения. Проверьте правильность полученных результатов – см. рис. 2.8.
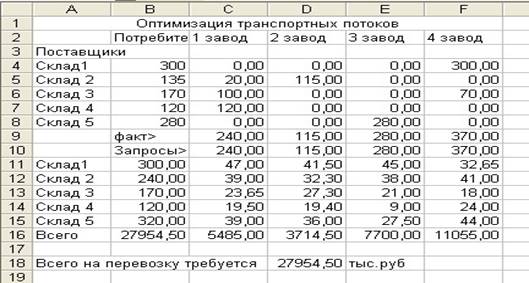
Рис. 2.8
I. Решить симплекс-методом следующие задачи линейного программирования.
1. Составить математическую модель.
2. Найти оптимальное решение.
3. Проанализировать его (результаты, устойчивость, пределы).
4. Провести параметрический анализ по одному из видов ресурсов (выбрать самостоятельно). Составить диаграммы зависимостей (см.
рис. 2.2, 2.3 и 2.4)
Вариант 1.
|
Тип Ресурса |
|
Вид изделий |
|
Всего ресурсов |
|
|
А |
В |
С |
D |
||
|
Трудовые |
2 |
2 |
2 |
2 |
30 |
|
Сырье |
12 |
10 |
8 |
6 |
150 |
|
Финансы |
8 |
12 |
20 |
25 |
200 |
|
Прибыль c(i) |
100 |
150 |
200 |
250 |
|
Вариант 2.
|
Тип Ресурса |
|
Вид изделий |
|
Всего ресурсов |
|
|
А |
В |
С |
D |
||
|
Трудовые |
1 |
2 |
1 |
2 |
15 |
|
Сырье |
8 |
10 |
6 |
4 |
100 |
|
Финансы |
6 |
4 |
12 |
15 |
120 |
|
Прибыль c(i) |
100 |
150 |
200 |
250 |
|
Вариант 3.
|
Тип Ресурса |
|
Вид изделий |
|
Всего ресурсов |
|
|
А |
В |
С |
D |
||
|
Трудовые |
10 |
8 |
6 |
2 |
100 |
|
Сырье |
5 |
10 |
4 |
15 |
150 |
|
Финансы 1 |
6 |
8 |
8 |
4 |
100 |
|
Финансы 2 |
15 |
10 |
10 |
10 |
200 |
|
Прибыль c(i |
30 |
30 |
30 |
30 |
|
Вариант 4.
|
Тип Ресурса |
|
Вид изделий |
|
Всего ресурсов |
|
|
А |
В |
С |
D |
||
|
Трудовые |
10 |
6 |
6 |
4 |
100 |
|
Сырье |
6 |
12 |
5 |
15 |
150 |
|
Финансы 1 |
6 |
10 |
10 |
4 |
100 |
|
Финансы 2 |
10 |
15 |
10 |
15 |
150 |
|
Прибыль c(i |
20 |
20 |
20 |
20 |
|
Вариант 5.
|
Тип Ресурса |
Вид издел |
ий |
Всего ресурсов |
|
|
A |
B |
C |
||
|
Сырье 1 |
10 |
6 |
6 |
100 |
|
Cырье 2 |
6 |
12 |
5 |
150 |
|
Трудовые |
6 |
10 |
10 |
100 |
|
Финансы |
10 |
15 |
10 |
150 |
|
Прибыль c(i) |
40 |
40 |
40 |
|
Вариант 6.
|
Тип Ресурса |
В |
ид издел |
ий |
Всего ресурсов |
|
A |
B |
C |
||
|
Сырье |
1 |
2 |
1 |
10 |
|
Трудовые |
2 |
1 |
2 |
6 |
|
Финансы |
3 |
1 |
2 |
10 |
|
Прибыль c(i) |
6 |
6 |
6 |
|
Вариант 7.
|
Тип Ресурса |
В |
ид издел |
ий |
Всего ресурсов |
|
A |
B |
C |
||
|
Трудовые |
1 |
2 |
1 |
10 |
|
Cырье |
2 |
1 |
2 |
6 |
|
Финансы |
3 |
1 |
2 |
12 |
|
Прибыль c(i) |
3 |
4 |
4 |
|
Вариант 8.
|
Тип Ресурса |
|
Вид изделий |
|
Всего ресурсов |
|
|
А |
В |
С |
D |
||
|
Трудовые |
1 |
3 |
4 |
7 |
15 |
|
Сырье |
2 |
1 |
3 |
4 |
10 |
|
Прибыль |
-1 |
1 |
2 |
4 |
|
Вариант 9.
|
Тип Ресурса |
|
Вид изделий |
|
Всего ресурсов |
|
|
А |
В |
С |
D |
||
|
Трудовые |
1 |
2 |
1 |
1 |
20 |
|
Сырье |
6 |
8 |
10 |
4 |
100 |
|
Финансы |
4 |
6 |
15 |
12 |
100 |
|
Прибыль c(i) |
60 |
70 |
120 |
100 |
|
Вариант 10.
|
Тип Ресурса |
Вид издел |
ий |
Всего ресурсов |
|
|
A |
B |
C |
||
|
Сырье 1 |
6 |
10 |
5 |
150 |
|
Cырье 2 |
10 |
6 |
6 |
100 |
|
Трудовые |
6 |
10 |
10 |
100 |
|
Финансы |
10 |
15 |
10 |
150 |
|
Прибыль c(i) |
40 |
40 |
40 |
|
II. Решить транспортные задачи.
Ответ представить в виде таблицы (см. рис. 2.8).
Вариант 1. Вариант 2.
|
ai \ bj |
100 |
200 |
200 |
300 |
|
ai \ bj |
200 |
400 |
400 |
800 |
|
100 |
1 |
3 |
4 |
1 |
200 |
1 |
6 |
9 |
3 |
|
|
200 |
5 |
2 |
2 |
7 |
400 |
3 |
2 |
2 |
4 |
|
|
400 |
4 |
4 |
3 |
6 |
600 |
4 |
5 |
4 |
7 |
|
|
200 |
7 |
2 |
5 |
3 |
200 |
1 |
4 |
3 |
9 |
Вариант 3. Вариант 4.
|
ai \ bj |
300 |
200 |
300 |
100 |
|
ai \ bj |
200 |
300 |
400 |
200 |
|
300 |
3 |
4 |
3 |
1 |
200 |
1 |
3 |
4 |
2 |
|
|
200 |
2 |
3 |
5 |
6 |
200 |
1 |
2 |
4 |
1 |
|
|
100 |
1 |
2 |
3 |
3 |
300 |
3 |
4 |
5 |
9 |
|
|
200 |
4 |
5 |
7 |
9 |
300 |
6 |
3 |
7 |
6 |
|
|
150 |
6 |
7 |
5 |
3 |
100 |
3 |
4 |
5 |
6 |
Вариант 5. Вариант 6.
|
ai \ bj |
100 |
200 |
300 |
200 |
|
ai \ bj |
300 |
200 |
200 |
400 |
|
300 |
3 |
3 |
3 |
1 |
200 |
1 |
3 |
4 |
2 |
|
|
200 |
2 |
3 |
5 |
4 |
300 |
1 |
2 |
4 |
2 |
|
|
100 |
5 |
2 |
3 |
3 |
300 |
3 |
4 |
4 |
8 |
|
|
200 |
4 |
5 |
7 |
6 |
200 |
6 |
6 |
7 |
3 |
Вариант 7. Вариант 8.
|
ai \ bj |
200 |
150 |
100 |
200 |
|
ai \ bj |
400 |
100 |
100 |
150 |
|
200 |
3 |
4 |
3 |
1 |
150 |
1 |
3 |
4 |
2 |
|
|
300 |
2 |
3 |
5 |
6 |
150 |
1 |
2 |
4 |
1 |
|
|
150 |
1 |
2 |
3 |
3 |
300 |
3 |
4 |
5 |
9 |
|
|
100 |
4 |
5 |
7 |
9 |
200 |
6 |
3 |
7 |
6 |
Вариант 9. Вариант 10.
|
ai \ bj |
300 |
200 |
300 |
100 |
|
ai \ bj |
200 |
300 |
400 |
200 |
|
300 |
3 |
4 |
3 |
1 |
200 |
1 |
3 |
4 |
2 |
|
|
200 |
2 |
3 |
5 |
6 |
200 |
1 |
2 |
4 |
1 |
|
|
100 |
1 |
2 |
3 |
3 |
300 |
3 |
4 |
5 |
9 |
|
|
200 |
4 |
5 |
7 |
9 |
300 |
6 |
3 |
7 |
6 |
|
|
150 |
7 |
6 |
5 |
4 |
100 |
8 |
5 |
6 |
4 |
1.Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование.М.: Высшая школа, 1980.
2. Матвеев В.И., Сагитов Р.В., Шершнев В.Г. Курс линейного программирования. М.: Менеджер, 1998.
3. Завьялова Н.Б., Бирюкова Л.Г., Киселева Е.В., Конева И.А. Решение задач линейного программирования средствами MS OFFICE. М., 2000.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.