
Решение задач «на движение»
с помощью систем уравнений
Цели: продолжить формирование умения решать задачи с помощью систем уравнения, уделив особое внимание задачам «на движение»; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
1. Являются ли данные системы уравнений равносильными:
а) 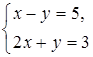 и
и 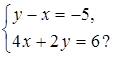
б) 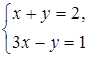 и
и 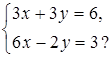
2. Придумайте ситуацию, которая описывается следующей системой уравнений:
а) 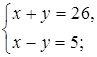 б)
б) 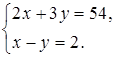
II. Формирование умений и навыков.
Сначала необходимо актуализировать знания учащихся. Они должны вспомнить, как используется таблица при решении задач «на движение» и какая существует зависимость между величинами s, υ и t.
1. № 1108.
2. № 1110.
Решение:
Обозначим скорости автомобилей через х км/ч и у км/ч. Выделим процессы: движение автомобилей навстречу друг другу и движение в одном направлении. Соответственно заполним две таблицы.
Движение навстречу
|
|
s |
υ |
t |
|
1-й автомобиль |
2х км |
х км/ч |
2 ч |
|
2-й автомобиль |
2у км |
у км/ч |
2 ч |
Получаем уравнение: 2х + 2у = 280.
Движение в одном направлении
|
|
s |
υ |
t |
|
1-й автомобиль |
14х км |
х км/ч |
14 ч |
|
2-й автомобиль |
14у км |
у км/ч |
14 ч |
Получаем уравнение: 14х – 14у = 280.
Составим и решим систему уравнений:
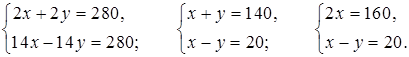
2х = 160;
х = 80;
80 – у = 20;
у = 60.
Ответ: 80 км/ч и 60 км/ч.
3. № 1111.
4. № 1113.
Решение:
Пусть х км/ч – собственная скорость теплохода, а у км/ч – скорость течения реки. Выделим процессы: движение теплохода по течению и против течения реки в первом и во втором случаях.
|
|
s |
υ |
t |
|
по течению |
3 (х + у) км |
(х + у) км/ч |
3 ч |
|
против течения |
4 (х – у) км |
(х – у) км/ч |
4 ч |
Получим уравнение: 3 (х + у) + 4 (х – у) = 380.
|
|
s |
υ |
t |
|
по течению |
(х + у) км |
(х + у) км/ч |
1 ч |
|
против течения |
0,5 (х – у) км |
(х – у) км/ч |
0,5 ч |
Получим уравнение: (х + у) + 0,5 (х – у) = 85.
Составим и решим систему уравнений:
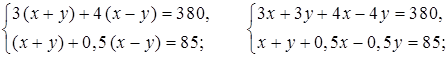
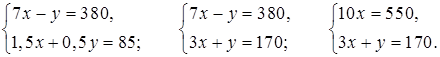
10х = 550;
х = 55;
3 · 55 + у = 170;
у = 170 – 165;
у = 5.
Ответ: 55 км/ч и 5 км/ч.
III. Проверочная работа.
Вариант 1
1. У Толи 18 монет по 2 р. и по 5 р. на сумму 97 р. Сколько монет каждого достоинства у Толи?
2. Поезд прошёл первый перегон за 2 ч, а второй за 3 ч. Всего за это время он прошёл 330 км. Найдите скорость поезда на каждом перегоне, если на втором перегоне она была на 10 км/ч больше, чем на первом.
Вариант 2
1. У Лены 8 монет по 10 р. и 5 р. Сколько у неё десятирублёвых и сколько пятирублёвых монет, если всего у неё 65 р.?
2. Туристы прошли 24 км, причём 3 ч дорога шла в гору, а 2 ч – под гору. С какой скоростью туристы шли в гору и с какой под гору, если на первом участке их скорость была на 2 км/ч меньше, чем на втором?
IV. Итоги урока.
– Как решаются задачи с помощью систем уравнений?
– Как используется таблица при решении задач «на движение»?
Домашнее задание: № 1106, № 1109, № 1112.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.