Решение задач на формулы сложения. Алгебра.

Решение задач на формулы сложения.

Часть 1. Допишите формулу:

1.     cos ( ɑ + β) = …

2.     tg ( ɑ - β) = …

3.     sin ( ɑ + β) = …

4.     tg ( ɑ +β) = …

5.     cos ( ɑ - β) = …

6.     sin ( ɑ - β) = …

Часть 2. Разберите  решение примеров на формулы сложения.

Пример 1. Вычислите значение  sin 105°

Решение.

Воспользуемся формулой №3, представим угол 105° через табличные углы:

105° = 45° + 30°.      Тогда sin 105° =sin (45° +30°) .  α = 45° , β=30°.

По формуле №3 :  sin 105° =sin (45° +30°)= sin 45°˔ cos 30° + cos45° ˔ sin 30°.

Воспользуемся таблицей значений тригонометрических функций.

˔  + ˔ = ( √3 +1).      Ответ:  ( √3 +1).

Пример 2.  Упростите и вычислите значение  выражения  

Cos 5x  ˔ Cos x  + sin 5x  ˔ sin x                   при х =

Решение.

                Воспользуемся формулой №5  в обратном  направлении:

                  Cos 5x  ˔ Cos x  + sin 5x  ˔ sin x  = Cos (5x –x) = Cos 4x  

Подставим вместо х заданное значение:

 Cos 4˔ = Cos  =   .            Ответ:  0, 5

Пример  3.  Вычислите значение  выражения    при х =.

Решение.

Воспользуемся формулой № 4 в обратном направлении.  Для этого заменим √3= tg . 

Подставим в исходное выражение вместо √3 выражение  tg, тогда по формуле №4 получим:

(tg+ tgx) : ( 1 - tg˔ tgx) = tg (+x) = tg (  +) = tg π = 0

                                                                              Ответ:  0

Пример  4.  Вычислите значение  130˔sin ( α –β ) , если cos α= ;     <α<2π, 

sin β= - ;    π < β < .

Решение.

По формуле №6   sin ( ɑ - β) = sin α˔ cos β - cosα ˔ sin β.

                                                     ?         ?               -

В этом выражении неизвестны значения  sin α   и   cos β.

Вычислим их, воспользовавшись основным тригонометрическим тождеством:     sin ² α + cos ² α =1.

sin α =±  . Угол α по условию принадлежит  IV четверти,  где sin α < 0.  Sin α = -  = -

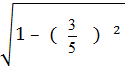cos β  = ± Угол β по условию принадлежит  III четверти, 

где cos β < 0              cos β  = -= - .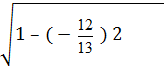

Подставим в формулу №6 все числа: 130 ˔(  (- ) ˔ (- ) -  ˔ (- ) ) = -32.

Ответ: - 32.

Часть 3. Решите самостоятельно:

1.     Вычислить  sin ( +α ),  если sin α =;   < α < π.

2.     Вычислить  cos 15°. = -

3.     Вычислить 17˔(sin 38°˔cos 52°+ cos 38°˔sin 52°)

4.     Вычислить  5˔ sin ( α + β) ,         если      sin α =  ;      0< α < ,

           sin β = -;     π < β < .

5.      Вычислить tg ( α –β) , если   tg α = - 0,25    tg β = 2,56.

6.     Вычислить  10˔sin ( - x)˔ cos x + 10 ˔ sin x˔ cos ( - x).

7.     Вычислить  6˔(sin 7α ˔cos5α  -  cos7α ˔sin 5α)   при   α =15°.

8.     Вычислить  tg 75°

9.     Упростить и вычислить  cos (α – β) + sin (- α)˔ sin β, если cos α = 0,7   cos β= - 0,25.

10.   Известно, что α и β  - углы II четверти и sin α = , cos β = - . Найдите :

а)  sin (α + β)

б)  sin (α - β)

в)   cos (α + β)

д)  cos (α - β)

е)  tg (α + β)

ж)  tg (α - β).

    11.  Упростить  выражение и вычислить, если sin α = - и угол   <α<2π,

                                 Cos (30° + α) - Cos (30° - α).

11. Вычислить  6˔tg ( + α), если cos α =      - <α< 0.