Практическая работа №3

Тема Решение задач оптимизации средствами табличного процессора MS Excel

Цель: - приобретение навыков решения задач оптимизации в табличном редакторе Microsoft Excel.

Вид работы: фронтальный

Время выполнения: 2 часа

Задания к практической работе

Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:

Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной.

Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:

1.            Для определения каких величин строится модель?

2.           В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?

3.            Каким ограничениям должны удовлетворять неизвестные?

В данном случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются: х1 - количество столов, х2 - количество шкафов

Суммарная прибыль от производства столов и шкафов равна z=6*x₁+8*x₂. Целью фабрики является определение среди всех допустимых значений х₁ и х₂ таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z

Ограничения, которые налагаются на х₁ и х₂:

·       объем производства шкафов и столов не может быть отрицательным, следовательно: х₁, х₂ ³ 0.

·       нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно:

0.2x₁+ 0.1x₂ £40

0.1x₁ +0.3x₂ £60

Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов

1.2x₁+ 1.5х₂ £ 371.4

Таким образом, математическая модель данной задачи имеет следующий вид:

Максимизировать

z = 6х₁ + 8х₂

при следующих ограничениях:

0.2x₁+ 0.1x₂ £40

0.1x₁ +0.3x₂ £60

1.2x₁+ 1.5х₂ £ 371.4

Данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.

Ход работы

1. Отвести ячейки A3 и ВЗ под значения переменных х₁ и х₂ (рис. 1).

Рисунок 1 - Диапазоны, отведенные под переменные, целевую функцию и ограничения

2. В ячейку С4 ввести функцию цели: =6*АЗ+8*ВЗ, в ячейки А7:А9 ввести левые части ограничений:

 =0,2*А3+0,1*ВЗ

 =0,1*А3+0,3*ВЗ

 = 1,2*АЗ+1,5*ВЗ,

а в ячейки В7:В9 - правые части ограничений. (рис.1.)

3. Выбрать команды Данные/Поиск решения и заполнить открывшееся диалоговое окно Поиск решения как показано на рис 2. Средство поиска решений является одной из надстроек Excel. Если в меню Данные отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду / Параметры Excel/ Надстройки/ Пакет анализа / / Поиск решения.

Для ввода ограничений нажмите кнопку Добавить.

Внимание! В диалоговом окне Параметры поиска решения необходимо установить флажок Линейная модель (Рис.3.).

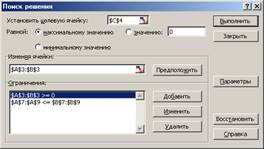
Рисунок 2 - Диалоговое окно Поиск решения задачи о максимизации прибыли на фабрике

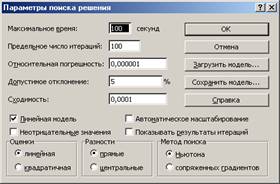
Рисунок 3 - Параметры поиска решения

4. После нажатия кнопки Выполнить открывается окно Результаты поиска решения, которое сообщает, что решение найдено (рис. 4).

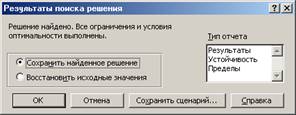
Рисунок 4 - Результаты поиска решения

5. Результаты расчета задачи представлены на рис. 5,  из которого видно, что оптимальным является производство 102 столов и 166 шкафов. Этот объем производства принесет фабрике 1940 руб. прибыли.

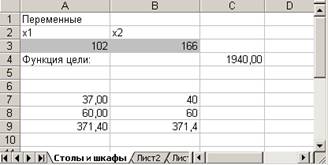
Рисунок 5 - Результаты расчета

Задание 2. «Транспортная задача»

Контрольный пример

Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы располагаются в Денвере, Бостоне, Новом Орлеане и Далласе с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице «Транспортные расходы»:

Таблица «Транспортные расходы»

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

·       Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции.

Для решения данной задачи построим ее математическую модель.

Неизвестными в данной задаче являются объемы перевозок. Пусть x_ij  - объем перевозок с i-ой фабрики в j-й центр распределения. Функция цели - это суммарные транспортные расходы, т. е. где с_ij – стоимость перевозки единицы продукции с i-и фабрики j-й центр распределения.

Неизвестные в данной задаче должны удовлетворять следующим ограничениям:

·       Объемы перевозок не могут быть отрицательными.

·       Так как модель сбалансирована, то вся продукция должна быть вывезена с      фабрик, а потребности всех центров распределения должны быть полностью удовлетворены.

В результате имеем следующую модель: Минимизировать:

при ограничениях:

, j Î [1,5]

x_ij ³ 0, iÎ [1,4], jÎ [1,5

, iÎ [1,4],

где a_ij - объем производства на i-й фабрике, b_j — спрос в j-м центре распределения.

Решение задачи с помощью MS Excel

1.     Ввести данные, как показано на рис. 6.

В ячейки А1:Е4 введены стоимости перевозок. Ячейки А6:Е9 отведены под значения неизвестных (объемы перевозок). В ячейки G6:G9 введены объемы производства на фабриках, а в ячейки А11:Е11 введена потребность в продукции в пунктах распределения. В ячейку F10 введена целевая функция =СУММПРОИЗВ(А1:Е4;А6:Е9).

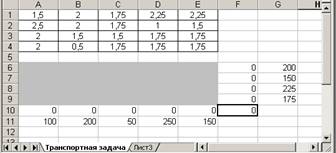
Рисунок 6 - Исходные данные транспортной задачи

В ячейки А10:Е10 введены формулы

=СУММ(А6:А9)

=СУММ(В6:В9)

=СУММ(С6:С9)

=СУММ(06:О9)

=СУММ(Е6:Е9) определяющие объем продукции, ввозимой в центры распределения.

В ячейки F6:F9 ведены формулы

=СУММ(А6:Е6)

=СУММ(А7:Е7)

=СУММ(А8:Е8)

=СУММ(А9:Е9) вычисляющие объем продукции, вывозимой с фабрик.

2.     Выбрать команду Данные/Поиск решения и заполнить открывшееся диалоговое окно Поиск решения, как показано на рис. 7.

Внимание! В диалоговом окне Параметры поиска решения необходимо установить флажок Линейная модель.

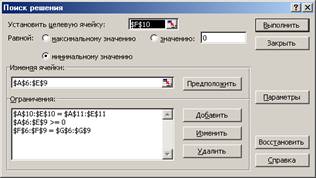
Рисунок 7 - Диалоговое окно Поиск решения для транспортной задачи

3.     После нажатия кнопки Выполнить средство поиска решений находит оптимальный план поставок продукции и соответствующие ему транспортные расходы (рис. 8).

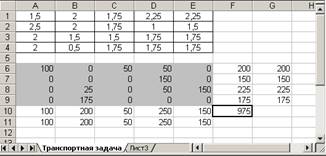
Рисунок 8 - Оптимальное решение транспортной задачи

Контрольные вопросы

1.     Построить математическую модель задачи, согласно Вашего варианта (см. практическую работу №2).

2.     Решить задачу с помощью средства MS Exscel Поиск решения.

3.     Как строится математическая модель?

4.     По какой структуре решается задача в программе MS Exscel?

Скачано с www.znanio.ru