Решение задач с помощью кругов Эйлера.

При решении задач с использованием кругов Эйлера очень важно правильно нарисовать картинку, отображающую найденные запросы. В таблице на страницах 2-3 представлены наиболее часто встречаемые случаи.

Отметив области, которые надо найти по условию, поняв, что требуется найти, решить задачу визуально становится довольно просто.

Самые простые задачи – на два круга, немного сложнее – на три. Достаточно трудно изобразить четыре круга. К счастью, такие задачи предоставляют возможность сделать сокращения и свести решение задачи к трём кругам. Например, даны такие запросы.

 Какое количество страниц (в тыс.) будет найдено по запросу

(Леннон & Маккартни & Старр) | (Леннон & Маккартни & Харрисон)?

При решении этой задачи можно сократить в исходных запросах и в тех, что надо найти запрос «Леннон», так как он выступает здесь как общий множитель. В итоге, задача сведётся к трём кругам.

            Иногда надо круги рисовать не «ромашкой», а в ряд. Это бывает в задачах, в которых представлены запросы, в двух из которых нет пересечения. Например, в этой таблице запросов явно указано, что нет пересечения между Напряжённость и Пшеница

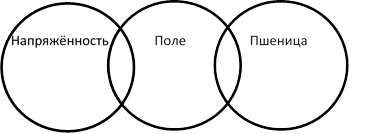
Картинка будет выглядеть так ->

Сложнее рисовать картинку в таком виде,

когда  пересечение равное 0 не задано и

надо догадаться, что у двух запросов нет

пересечения. Как правило, в центре располагается запрос, представляющий собой слово-омоним. Справа и слева от него значения запросов даны, а также дано бывает их объединение (ИЛИ). Например, если Пшеница – 40, Напряжённость – 44, а Напряжённость|Пшеница – 84, то складывая 40 и 44, понимаем, что пересечения нет, так как сумма и запрос ИЛИ  дают одно и то же число 84.

Ученикам, которые впервые решают задачи на круги Эйлера, бывает сразу не очень понятно, почему если есть значение двух запросов, то их объединение не равно их сумме. Понять это легко можно на следующем примере. Допустим, есть запросы Пушкин и Лермонтов. Изобразим, что всего было найдено 5 страниц. На каких то страницах речь шла только о Пушкине, на других только о Лермонтове, а где то писали о них обоих.

По картинке видно, что запрос Пушкин выдал 4 страницы, Лермонтов – 3, Пушкин&Лермонтов – 2, а Пушкин|Лермонтов – 5. Запрос ИЛИ не выдаст 7, так как из условия физически не существует столько страниц. Их всего 5.

Пушкин                                                   Лермонтов

«2» входит и в круг «Пушкин» и в круг «Лермонтов», поэтому

Пушкин ИЛИ Лермонтов = 4 + 3 - 2 = 5