РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ

Решение задач с помощью уравнений

Цели: продолжить формировать умение решать текстовые задачи алгебраическим методом – с помощью составления уравнений, сводящихся к линейным.

Ход урока

I. Устная работа.

1. Вычислите.

а) 0,35 · 0,2 + 0,35 · 0,8;        в) ;                          д) ;б)  · 0,5 · 8;        г) ;    е) (–3)² – 9,2.

2. Выразите:

а) t     из   s = υ · t;                   в) y   из   υ = 2a – y;

б) p   из   N = p : t;                   г) x   из   y = .

II. Проверочная работа.

Вариант 1

1. Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый рабочий?

2. Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?

Вариант 2

1. В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?

2. У Коли и Пети вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого мальчика?

III. Формирование умений и навыков.

При решении задач замечаем, что неизвестную величину не обязательно  обозначаем  за  х.  Наоборот,  если  в  задаче  используется  формула, например, s = υ · t, то и переменную удобно обозначать соответствующей буквой.

1. № 151.

Решение:

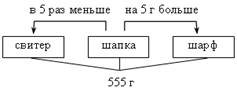
Пусть х г шерсти ушло на шапку, тогда на свитер ушло 5х г, а на шарф – (х – 5) г шерсти. Зная, что на все изделия ушло 555 г шерсти, составим уравнение:

х + 5х + (х – 5) = 555;

х + 5х + х – 5 = 555;

7х = 560;

х = 80.

Значит, на шапку ушло 80 г шерсти. Так как 5х = 5 · 80 = 400, то на свитер ушло 400 г шерсти.

Так как х – 5 = 80 – 5 = 75, то на шарф ушло 75 г шерсти.

Ответ: 400 г; 80 г; 75 г.

2. № 152.

Решение:

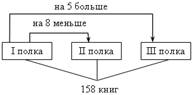
Пусть  на  первой  полке  расположено  п  книг,  тогда  на  второй  полке – (п + 8), а на третьей – (п – 5) книг. Зная, что на трех полках необходимо расположить всего 158 книг, составим уравнение:

п + (п + 8) + (п – 5) = 158;

п + п + 8 + п – 5 = 158;

3п + 3 = 158;

3п = 155;

п = 51.

Интерпретация результата: так как п – число книг, то п дол-жно быть натуральным числом. 51 – дробное, значит, указанным способом нельзя разместить книги на полках.

Ответ: нельзя.

На примере этой задачи видно, что важен этап интерпретации полученного решения.

3. № 154.

Решение:

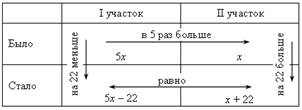
Пусть х кустов малины было на втором садовом участке, тогда на первом было 5х кустов. После пересадки на первом участке осталось (5х – 22) кустов малины, а на втором стало (х + 22) куста малины. Зная, что после пересадки  на  обоих  участках  стало  кустов  малины  поровну,  составим уравнение:

5х – 22 = х + 22;

5х – х = 22 + 22;

4х = 44;

х = 11.

Значит,  на  втором  участке  было  11  кустов  малины.  Так  как  5х =
= 5 · 11 = 55, то на первом участке было 55 кустов малины.

Ответ: 55 и 11 кустов малины.

4. № 155.

Решение:

Анализ условия:

Пусть υ_c км/ч – собственная скорость теплохода, тогда по течению он шел со скоростью (υ_c + 2) км/ч и за 9 часов прошел 9 · (υ_c + 2) км. Против течения он шел со скоростью (υ_c – 2) км/ч и прошел 11 · (υ_c – 2) км. Зная, что он прошел по течению и против одинаковое расстояние, составим уравнение:

9 · (υ_c + 2) = 11 · (υ_c – 2);

9 υ_c + 18 = 11 υ_c – 22;

9 υ_c – 11 υ_c = – 22 – 18;

–2 υ_c = –40;

υ_c = 20.

Значит, собственная скорость теплохода равна 20 км/ч.

Ответ: 20 км/ч.

При обозначении переменной можно не ставить индекс υ_c, а просто обозначить υ. Не возбраняется использовать любую букву латинского алфавита.

5. № 157.

Решение:

Пусть второй человек догонит первого через п дней, тогда за эти дни он пройдет 45п верст. Первый человек, так как он шел на день дольше, пройдет 40 (п + 1) верст. Зная, что они пройдут одинаковое расстояние, составим уравнение:

45п = 40 (п + 1);

45п = 40п + 40;

45п – 40п = 40;

5п = 40;

п = 8      Значит, через 8 дней второй догонит первого.

IV. Итоги урока.

Домашнее задание: № 150, № 153, № 156, № 248.