РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ3

Решение задач с помощью уравнений

Цель: продолжить формировать умение решать текстовые задачи алгебраическим методом – с помощью составления уравнений, сводящихся к линейным.

Ход урока

I. Организационный момент

II. Формирование умений и навыков.

1. № 158.

Решение:

Анализ условия:

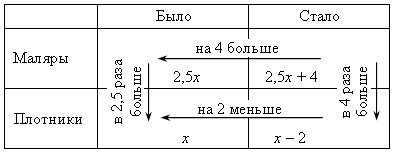
Пусть х плотников было в бригаде, тогда маляров было 2,5х. После переводов в бригаде стало (2,5х + 4) маляров и (х – 2) плотников. Зная, что маляров стало в 4 раза больше плотников, составим уравнение:

(2,5х + 4) = 4 · (х – 2);

2,5х + 4 = 4х – 8;

2,5х – 4х = –8 – 4;

–1,5х = –12;

х = (–12) : (–1,5);

х = 8.

Значит, в бригаде было 8 плотников. Так как 2,5х = 2,5 · 8 = 20, то в бригаде было 20 маляров.

Ответ: 20 маляров и 8 плотников.

В таблице основную зависимость, по которой формируем равенство, можно выделить другим цветом или более жирной линией.

2. № 161.

Решение:

Анализ условия:

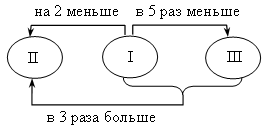
Пусть х кг – масса первого арбуза, тогда второй арбуз весит (х + 2) кг, а третий – 5х кг. Первый и третий арбуз вместе весят х + 5х, то есть 6х кг. Зная, что в сумме они весят в 3 раза больше второго арбуза, составим уравнение:

3 · (х + 2) = 6х;

3х + 6 = 6х;

3х – 6х = –6;

–3х = –6;

х = 2.

Значит, первый арбуз весит 2 кг. Так как х + 2 = 2 + 2 = 4, то второй арбуз весит 4 кг. Так как 5 · х = 5 · 2 = 10, то третий арбуз весит 10 кг.

Ответ: 2 кг, 4 кг, 10 кг.

3. № 162.

Решение:

Анализ условия:

Пусть х кг сахара взяли из первого мешка, тогда из второго мешка взяли 3х кг сахара. В первом мешке осталось (50 – х) кг сахара, а во втором – (50 – 3х) кг. Зная, что во втором мешке осталось в 2 раза меньше сахара, чем в первом, составим уравнение:

2 · (50 – 3х) = 50 – х;

100 – 6х = 50 – х;

–6х + х = 50 – 100;

–5х = –50;

х = (–50) : (–5);

х = 10.

Значит,  из  первого  мешка  взяли  10  кг  сахара.  Так  как  50 – х =
= 50 – 10 = 40, то в первом мешке осталось 40 кг сахара. Так как 50 – 3х =
= 50 – 3 · 10 = 50 – 30 = 20, то во втором мешке осталось 20 кг сахара.

Ответ: 40 кг и 20 кг.

4. Федя на 7 лет старше Пети, а их папе в 3 раза больше лет, чем им обоим вместе. Сколько лет каждому из них, если папе было 36 лет, когда родился Петя?

Решение:

Анализ условия:

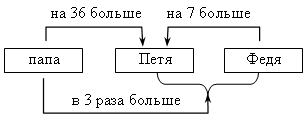
Пусть х лет Пете, тогда Феде (х + 7) лет, а папе (х + 36) лет. Пете и Феде вместе х + (х + 7) лет или 2х + 7 лет. Зная, что папе лет в 3 раза больше, чем им обоим вместе, составим уравнение:

(2х + 7) · 3 = х + 36;

6х + 21 = х + 36;

6х – х = 36 – 21;

5х = 15;

х = 3.

Значит, Пете 3 года. Так как х + 7 = 3 + 7 = 10, то Феде 10 лет.

Ответ: Пете 3 года, Феде 10 лет.

III. Проверочная работа.

Вариант 1

Стоимость изделия третьего сорта в 3 раза меньше стоимости изделия первого сорта. Сколько стоит каждое изделие, если изделие первого сорта на 5000 р. дороже изделия третьего сорта?

Вариант 2

Мама весит в 5 раз больше дочери, а дочь на 40 кг легче мамы. Сколько весят мама и дочь в отдельности?

IV. Итоги урока. Домашнее задание: 1. № 159, № 160, № 252.