РОЛЬ МАТЕМАТИЧЕСКОЙ ОСОБЕННОСТИ В ВОСПИТАНИИ ЛОГИКИ НА УРОКАХ ГЕОМЕТРИИ

Роль МАТЕМАтиЧЕСКой ОСОБЕННОСТи В воспитаниИ Логики НА уроках геометрии

А.О. Даутов¹, А.Б. Жаныс², С. Н. Нуркасымова³, А.Н. Бейсеков⁴

¹Кокшетауский государственный университет им. Ш. Уалиханова

²Казахский агротехнический университет им. С. Сейфуллина

³Евразийский национальный университ им.Л.Н. Гумилева

⁴Кокшетауский технический институт КЧС МВД РК

Аннотация. В данной статье рассматривается один из методических подходов к решению классических задач по курсу геометрии. Особенность статьи заключается в применении таких математических особенностей качеств, как: логическое мышление, культурная роль личности, на основе которых геометрическая задача выглядела бы методо-формирующим. Использование в геометрии элементов логики способствует развитию умений и навыков каждого обучаемого.

Ключевые слова: учебно-воспитательный процесс, роль предмета «Геометрия», интегративный подход, критерий развития, логическое мышление.

A.O. Dautov¹, A.B. Zhanys², S.N. Nurkassymova³, A.N. Beisekov⁴

¹Kokshetau State University named after S. Ualikhanov

²Kazakh Agrotechnical University after named S. Seifullin

³Eurasian National University after named L.N. Gumilev

⁴Kokshetau Technical Institute of CES MIA of the Republic of Kazakhstan

Annotation. This article discusses one of the methodological approaches to solving classical problems in the course of geometry. The peculiarity of these article lice is the application such mathematical features of qualities as: the logical thinking, the cultural role of personality, on the basis of which the geometric problem would look methodically formative. The use of elements of logic in geometry contributes to the development of skills and abilities of each student.

Keywords: educational process, organization the role "Geometry" lessons, integrative approach, criterion of development, logical thinking.

Каждый человек способен эмоционально воспринимать мир, чувствовать красоту природы. Но не каждый может перевести свои эмоции в сферу геометрической части объекта, прийти к созданию иллюстративного образа. Способность видеть красоту имеет не только тот, кто духовно воспитан, но и обладает фантазией, мышлением, логическим воображением. Обучаемый, владеющий вышеперечисленными свойствами, сможет создавать свои суждения, а также делать высказывания к той или иной задаче.

В настоящее время широко применяется термин «задача» как в жизни, так и в науке. Этим термином обозначаются многие и весьма различные понятия, но на сегодняшний день нет точного определения понятия «задача».

В широком смысле задача рассматривается как проблемная ситуация с явно заданной целью, которую необходимо достичь каким-либо результатом. В более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать. Задача является проблемной ситуацией, которая выражается с помощью знаков естественного или научного языка, что считается, если субъект при выполнении какой-либо деятельности на своём пути встречает трудности, то в результате возникает проблемная ситуация. Значит, проблемная ситуация – это не просто трудности, возникающие на пути субъекта, а его желание и стремление их устранить [1].

Величайшая трудоспособность и волевое напряжение, мобилизация всех духовных, эмоциональных и интеллектуальных сил, сосредоточена на стремлении к глубокому проникновению, в сущности, времени, в котором мы живем. В таком случае, геометрические задачи должны отвечать не только на вопросы геометрии, но и на коренные социальные, политические, моральные вопросы времени, то есть быть универсальным духовным феноменом жизни [2].

Геометрия неизбежно влияет на развитие интеллекта, логики, творческих способностей, культуру обучающихся. Обращаясь к геометрическому чертежу, нужно понять, что это не просто изображение, он участвует в нашей жизни, помогает формировать нравственные качества обучающихся. Занимаясь чертежами геометрии, изображениями, можно сделать вывод, что они влияют на развитие творческих способностей, воспитания, формируя логическо-формирующее представление, восприятие. Именно во взаимоотношениях геометрических построений и геометрических чертежей удовлетворяются очень важные моменты, иллюстрирующие присутствие прекрасного и чисто человеческие потребности, чрезвычайно важные для роста всесторонней, особенной роли гармоничной и духовно развитой личности в становлении нашего общества.

Основным средством обучения геометрии, являются, задачи. Поэтому представляется, что эстетическое воспитание в процессе обучения геометрии целесообразно проводить, опираясь, в первую очередь, именно на решение задач.

Такая точка зрения согласуется с пересмотром характера действенности эстетического воспитания, происшедшим в последние годы. Большинство методистов и педагогов отказались от созерцательного взгляда на эстетическое воспитание в пользу его активно-действенного понимания. Проведение эстетического воспитания во взаимосвязи и единстве, с процессом обучения стало рассматриваться как необходимое условие успешного усвоения программного материала [3]. Говоря о роли математических особенностях воспитании, подразумевают, что развитие творческо-логических способностей является его составной частью. Если осуществлять логическую интерпретацию математических понятий, то это будет способствовать:

1)       повышению интереса к предмету «Геометрия»;

2)       сознательному усвоению геометрического материала;

3)       психолого-педагогическому воздействию во благо всесторонне развитой личности;

4)       стимулированию творческого отношения к изучаемому предмету и к миру красоты.

Важнейший принцип математического воспитания или обучения – активность субъекта. Таким образом, роль математического воспитания и логики нацелена на пробуждение инициативы и предприимчивости обучающихся, на логическое развитие  критического и образного мышления, на преодоление изживших себя иждивенческих настроений и всемерное возвышение нравственных понятии. Судьба каждого учащегося, вплетаясь в судьбу педагога, зависит от его собственных усилий, воли, стремлений, настойчивости, трудолюбия, а также укрепления нравственно-духовной стабильности в обществе.

Потверждением укрепления нравственно-духовной стабильности преподавания математики, в том числе, и ценности геометрических построений, их безупречной красоты, соблюдения цепочку логических приоритетов и т.д., безусловно оговаривает английский математикик и философ Альфред Прейнсгейм в статье «Ценность и мнимая неценность математика» [4].

Многие профессиональные математики и философы настаивают на несомненности существования своеобразного потенциала математики, хотя эти утверждения по большей части опираются лишь на эмоционально-чувственную или интеллектуально-интуитивную очевидность, поэтому у непрофессионалов возникает иногда сомнение или недоверие к подобным утверждениям. «…прекрасные черты» математики проявляются по-разному [5].

Традиционным методическим принципом преподавания геометрии постсоветского и настоящего времени в школах является принцип линейности изложения теории. Этот принцип предполагает последовательное изложение учебного материала, начиная с описания неопределяемых понятий, формулировки аксиом и строгого доказательства теорем и описания приложений соответствующей математической теории [6]. Значит, сущность планиметрических и стереометрических задач состоит в том, чтобы показать основы и принципы, делающие геометрию необходимой частью профессиональных знаний как важной составляющей человеческой культуры.

Полагаясь на идеи ученых по выявлению развития математического потенциала в обучении геометрии, попробуем раскрыть суть использования воспитаний и логики на примере геометрического построения одной задачи. Проблема методических и логических форм обучения как средства воспитания учебного процесса, имеет свои результаты, если в раскрытии потенциала логики можно определить значимость внедрения взаимосвязь математических компетенций и логики в процесс освоения предмета «Геометрия», познать красоту решения задач, выявить пути реализации практической работы «Одна задача – несколько решений» [7].

Путем формирования роли математических форм обучения может быть сконструировано звено по обобщению и закреплению знаний, умений и навыков на примере одной задачи. Таким образом, согласно практической деятельности обучающихся можно выявить те или иные звенья понимания геометрической простоты, то есть воспитательный потенциал логического представления при решении одной задачи различными способами. Приведем пример.

Задача. Постройте квадрат ABCD, три вершины которого лежат на трех данных параллельных прямых k; n; t.

Решение.

I способ. Очевидно, что окружность с центром в A радиуса AB пересекает прямую k в точке K такой, что ÐBKD = 45° (вписанный, равен половине угла BAD) – рис.1. Тогда из произвольной точки KÎk  проводим луч под углом 45° к этой прямой. Он пересечет t в вершине D. Серединный перпендикуляр к отрезку KD позволит получить вершину AÎn. Дальнейшее очевидно.

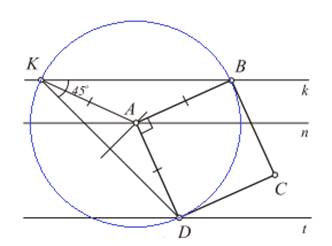
Рис. 1. Наглядный чертеж логического построения.

II способ – классический. При повороте вокруг точки AÎn на 90°, например, по часовой стрелке, вершина B перейдет в вершину D. Тогда прямая k₁ – образ прямой k при таком повороте вокруг точки A – пересечет прямую t в вершине D. Причем AD – сторона искомого квадрата – рис.2.

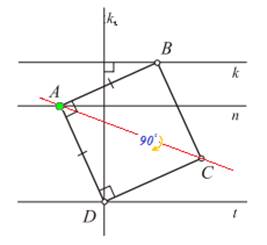
Рис. 2. Классический чертеж логического построения.

III способ. Полагаясь на построение рисунков 1 и 2, внесем изменения в квадрат ABCD дополнительные чертежи, что DABE = DDAF – по гипотенузе и острому углу. Отложив AF= BE (BE – расстояние между k и n) и проведя из F перпендикуляр к прямой t, получим вершину D – рис.3.

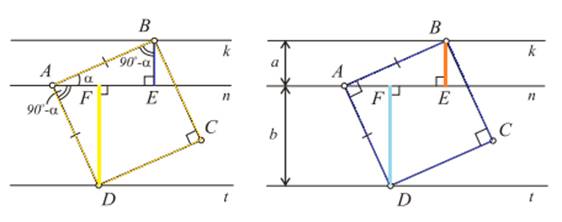
Рис. 3. Дополнительный чертеж логического построения.

В каждом из предложенных доказательств одной задачи, получен один и тот же результат с позиций ее красоты, роль математической ценности способствующий формированию понятий геометрической иллюстрации, а также имеет неотъемлемую часть в воспитании, которая является одной из важнейших составляющих в процессе логического представления познавательной деятельности обучающихся.

Итак, решение одной геометрической задачи несколькими доказательствами наглядно, а также визуального представления геометрических построений показывает, что существенным компонентом форм логического обучения и форсированности рассуждения как средства воспитания учебного процесса по геометрии, является овладение знаниями, связанными с пониманием творческого подхода к особенности математически.

СПИСОК ИСПОЛЬЗОВАНННЫХ ИСТОЧНИКОВ

1.    Фридман Л.М. Как научиться решать задачи: пособие для учащихся / Л. М. Фридман, Е.Н. Турецкий. – М.: Просвещение, 1984.

2.    Даутов А.О. и др. Решение математических задач с применением программных продуктов в процессе эстетического воспитания для студентов сельскохозяйственных специальностей // Поиск. – 2019, №3. С. 177-187.

3.    Фирстова Н.И. Эстетическое воспитание при обучении математике в средней школе: Учебное пособие. – М.: Прометей, 2013. 128 с.

4.    Нысанбаев А Н. Духовно-ценностный мир народа независимого Казахстана: проблемы и перспективы // Под общ. ред. З.К. Шаукеновой. – Алматы: Институт философии, политологии и религиоведения КН МОН РК, 2015. – 274 с.

5.    Даутов А.О., Далингер В.А. Обучение математике с использованием информационно-коммуникационных технологий как средство развития мышления и эстетического воспитания учащихся //НОУ ВПО «Сибирский институт бизнеса и информационных технологий». – 2019, №2 (30). С. 11-16.

6.    Даутов А.О., Кожабаев К.Г. и др. Применение эстетических форм обучения математике  в кокшетауском техническом институте // Журнал «Вестник Кокшетауского технического института». – 2019, № 4 (36), С. 86-93.

7.    Dautov A., Aktayeva Al., etc. [Электронный ресурс] – Режим доступа: https://znanio.ru/media/ 369619 – Aesthetic education: the Process of teaching mathematics with the Application of Information-Communicative Technologies.

Сведения об авторах:

1.        Даутов Айбек Омирбекович – PhD-докторант по специальности математика, Кокшетауского государственного университета им. Ш. Уалиханова. Кокшетау, Казахстан. E-mail: d.abeke@mail.ru

2.        Жаныс Арай Бошанкызы – Казахский агротехнический университет им. С. Сейфуллина, ст. преподаватель кафедры «Информационных систем», PhD, по специальности математика, профессор РАЕ № 7524. Нур-Султан, Казахстан. E-mail: aray.zhanys@gmail.com

3.        Нуркасымова Сауле Нуркасымовна – д.п.н., проф. кафедры общей и теоретической физики Евразийского национального университета им. Л.Н. Гумилев. Нур-Султан, Казахстан, E-mail: saulenurkasim@mail.ru

4.        Бейсеков Акылбек Нуртаевич – к.ф.-м.н., зав.каф., член-корреспондент АВН, подполковник Кокшетауский технический институт КЧС МВД РК. E-mail: b.akilbek@mail.ru

1.        Dautov A.О – PhD-doctorate specialty mathematics of Kokshetau State University after named Sh. Ualihanov. Kokshetau, Kazakhstan. E-mail: d.abeke@mail.ru

2.        Zhanys A.B. – Kazakh Agrotechnical University after named S. Seifullin, senior lecturer, department of «Information systems», PhD, specialty mathematics, professor RAE № 7524. Nur-Sultan, Kazakhstan. E-mail: aray.zhanys@gmail.com

3.        S.N. Nurkassymova – doctor of pedagogy, dept. of General and Theoretical Physics, Eurasian National University after named L.N. Gumilev. Nur-Sultan, Kazakhstan, E-mail: saulenurkasim@mail.ru

4.          Beisekov A.N. – Candidate of Physics and Mathematics, Head of Department, corresponding member of AMS, Colonel Kokshetau Technical Institute CSF MIA of RK. E-mail: b.akilbek@mail.ru

1.        Даутов А.О – Ш.Уәлиханов атындағы Көкшетау мемлекеттік университетінің, математика мамандығы бойынша PhD-докторанты. Көкшетау, Қазақстан. E-mail: d.abeke@mail.ru

2.        Жаныс А.Б. – С.Сейфуллин атындағы Қазақ агротехникалық университетінің, «Ақпараттық жүйелер» кафедрасының аға оқытушысы, PhD–математика, № 7524 РАЭ профессоры. Нур-Султан, Қазақстан. E-mail: aray.zhanys@gmail.com

3.        Нуркасымова С.Н. – п.ғ.д., жалпы және теориялық физика кафедрасың профессоры, Л.Н. Гумилев атындағы Еуразия ұлттық университеті. Нұр-Сұлтан, Қазақстан, E-mail: saulenurkasim@mail.ru

4.        Бейсеков А.Н. – физика-математика ғылымдарының кандидаты, кафедра меңгерушісі, АВН корреспондент-мүшесі, ҚР ІІМ ТЖК Көкшетау техникалық институтының полковнигі. E-mail:: b.akilbek@mail.ru

Скачано с www.znanio.ru