Ряд Фибоначи

Ֆիբոնաչիի պարադոքսը

            Ֆիբոնաչիի թվերի հետ անուղղակի ձևով կապված է մի հետաքրքրական երկրաչափական պարադոքս :

Միանգամայն ակնհայտ  է,  որ եթե որևէ հարթ պատկեր կտրտենք մի քանի մասերի,  այնուհետև ստացված մասերը կցենք իրար (բայց մեկը մյուսի վրաչ դնելով) ու կազմենք նոր պատկեր, ապա ստացված պատկերը իր ձևով կարող  է  տարբերվել սկզբնական պատկերից  ,  բայց նրա մակերեսը կմնա նույնը,  ոչ մի քառակուսի միավոր չի կարող ոչ ավելանալ,  ոչ` պակասել:  Այս ակնհայտ պնդումը երկրաչափությանայն հիմնական նախնական դրույթներից մեկն  է,  որոնց վրա կառուցվում   է  մակերեսների չափման ամբողջ տեսությունը:

              y                          x

                                                              y

                               x                                x+y

                                                              x                                                                                 x

                                                   նկ.1

            Նկար  1-ում ցույց  է տրված քառակուսու վերածումը ուղղանկյան:

Քառակուսին բաժանված  է երկու հավասար եռանկյունների    և   երկու հավասար սեղանների,  որոնց կողմերի երկարությունները նշանակում են

x   և  y    տառերով:  Այդ մասերից կազմված   է   ուղղանկյուն:  Եթե քառակուսու այդպիսի վերածումը ուղղանկյան իսկապես հնարավոր  է  ,  ապա քառակուսու կողմը ինչպիսի՞մասերի պետք  է  բաժանեն  x  -ը  և  y -ը:

Ֆիբոնաչչին վերցրեց 64  վանդականոց քառակուսին ու մտածեց այն մասին,  թե քառակուսու կողմը ինչպիսի     x    և   y    մասերի պետք  է  բաժանել: Սկզբում կարծեց,  թե դա նշանակություն չունի   և    ընդունեց

x=6,   y=2: Քառակուսին   նշագծեց,  բաժանեց  2  հավասար եռանկյունիների և  երկու հավասար սեղանների,  սկսեց կազմել ուղղանկյուն, ինչպես  1.նկարում,  ու ոչինչ դուրս չեկավ:  Իսկական ուղղանկյունչստացվեց նաև x  -ի  և  y -ի   ուրիշ արժեքների դեպքում օրինակ՝.,:

Միայն x =5,  y=3 արժեքների դեպքում կարողացավ քառակուսուս տացված մասերից կազմել ուղղանկյուն   ,  բայց այստեղ էլ ապշեց մի նոր տհաճությունից, ուղղանկյա նմակերեսը հավասար էր 65 վանդակի,  այսինքն՝1 վանդակով   մեծ էր սկզբում վերցված քառակուսու մակերեսից:

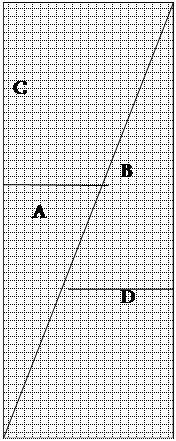
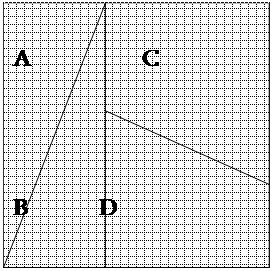
Դիտեքնկար 2-ը:

            Իրոք դատելով նախորդ նկարից,  ուղղանկյան երկարությունը պետք  է  պարունակի x+x+y=2x+y=2 ·5+3=13 միավոր, իր մոտ ստացվել էր ուղիղ 13  միավոր.  Ուղղանկյան լայնությունը x է, իր մոտ ողղանկյան լայնությունը ստացվել էր 5 միավոր: Այստեղից երևում  է,  որ նրա մակերեսը պարունակում  է  5 ·13=65  վանդակ,  բայց դա դեռ բոլորը չէ:

            Նույն ձևվածքով  (նկ 1.ում) նա մասերը բաժանեց   13 միավոր կողմ ունեցող մի ուրիշ քառակուսու:   Եթե վերցնում էր  x=8  և  y=5,  ապա քառակուսու մասերից ստացվում էր ուղղանկյուն,  բայց…  այս անգամ նրա մակերեսը փոքր էր լինում քառակուսու մակերեսից,   ընդ որում նույնպես   1   վանդակով:

            Քառակուսին պարունակում  է   13² =169 վանդակ, իսկ ուղղանկյան մակերեսը՝

                           (2x+y)·x=(2·8+5)·8=168 վանդակ    

            Եվս երկու օրինակ.

1.Վերցնում   է  21 x 21=441վանդականոց քառակուսի: Կողմը բաժանում է 

x=13, y=8  մասերի:  Կտրտում   է,  միացնում  է ,   ուղղանկյունը պատրաստ   է,  հաշվում   է   մակերեսը:

  (2x+y)·x=(2·13+8)·13=442 վանդակ

Դարձյալ մեկ վանդակ ավել  է  ստացվում:

2.  Վերցնում ենք  34 x 34=1156 վանդականոց քառակուսի:  Կողմը բաժանենք

x=21,  y=13  մասերի:

Կտրտենք:  Միացնենք:  Ուղղանկյունը ստացվեց,  հաշվենք մակերեսը.

  (2x+y)·x=(2·21+13)·21=1155  վանդակ:

            Մի վանդակ պակասում է: Ինչու՞.

            Հակառակ իր պնդումներին  ՝  նա ոչ մի անգամ քառակուսու մասերից չէր ստացել համատարած ուղղանկյուն ,  անպայման պետք  է   ճեղքեր լինեին: Քառակուսու կողմերի ինչպիսի՞ բաժանման դեպքում նա կստանար համատարած ուղղանկյուն,  դիմենք հանրահաշվի օգնությանը.

Քառակուսու մակերեսը՝ (նկ 1) S_ք=(x+y)²=x²+2xy+y²=S_ուղ=(2x+y)x=2x²+xy:

Ուղղանկյան  և քառակուսու մակերեսների  R  տարբերությունը՝ R=x²-xy-y²:

            Ուղղանկյան  և քառակուսու մակերեսները   իրար հավասար կլինեն,  եթե  x²-xy-y²=0

Բաժանելով y²-ու  վրա, կստանանք-ի  նկատմամբ քառակուսի հավասարում

Հաշվի առնելով միայն դրական լուծումները,  ունենք՝  

            Քառակուսին երկու հավասար եռանկյունների և   2 հավասար սեղանների բաժանելիս,  կողմերի  x և y մասերի միայն այդպիսի  (իռացիոնալ ) հարաբերության դեպքում է հնարավ որ քառակուսու լիարժեք ձևափոխումը ուղղանկյան:

            x-իև  y-ի ռացիոնալ արժեքների դեպքում   R  տարբերությունը չի կարող

հավասարվել  0-ի:    x-իև y-ի ամբողջ արժեքների դեպքում մակերեսների ամենափոքր հնարավոր տարբերությունը՝  R=1: Ահա այդ ամենափոքր ամբողջ տարբերությունն էր ստանում Ֆիբոնաչչին: