Самостоятельная работа №2 "Сумма и произведение вероятностей".

Задачи на теорию вероятностей. Сумма и  произведение  вероятностей.

Сумма вероятностей.

1.     На экзамене ученик достает один вопрос из списка. Вероятность, что на тему «Треугольник» равна 0,15, что на тему «Квадрат»  -  0,28, что на «Окружность»  - 0,3. Вопросов, которые относятся одновременно к этим трем темам нет. Найти вероятность, что достанется вопрос по одной из этих тем.

2.     В кармане 4 монеты по рублю и 2 монеты по два рубля. Три переложили в другой карман. Найти вероятность, что обе двухрублевые лежат в одном кармане.

3.     В кафе вероятность, что принесут миндальное печенье 0,1. Вероятность, что принесут мороженое 0,2. Какова вероятность, что принесут одно из этих двух.

4.     Вероятность, что чайник прослужит больше года равна 0,98, что больше двух лет 0,86. Какова вероятность, что меньше двух лет, но больше года?

5.     Вероятность, что телевизор  прослужит больше пяти лет равна 0,92, что больше десяти лет 0,39. Какова вероятность, что меньше десяти лет, но больше пяти лет?

6.      Вероятность, что П. на тестировании по математике решит больше семи задач равна 0,78, а больше шести равна 0,89. Найти вероятность, что П. решит ровно семь задач.

7.      Стрелок стреляет по мишени два раза. Вероятность попадания при первом выстреле равна 0,26, а при втором 0,32. Какова вероятность, что он поразит цель хотя бы при одном выстреле?

8.      В реке водятся пескари и караси. При одном закидывании удочки вероятность, что попадется пескарь равна 0,2, а что попадется карась равна 0,1.Найти вероятность, что при одном закидывании удочки рыбак ничего не поймает.

9.      Из районного центра в деревню ходит автобус. Вероятность, что в понедельник будет меньше 20 пассажиров равна 0,94, что меньше 15 равна 0,56. Найти вероятность, что пассажиров будет от 15 до 19.

10.  Два завода выпускают предохранители. Первый выпускает 40% торой – 60%.Первый выпускает 4 % бракованных, а второй – 3 %. Найти вероятность, что попадется бракованный.

11.  Три фабрики выпускают шины. Первая – 30%, вторая 45%,  третья – 25 %. Первая дает 3 %  брака, вторая – 6 %, третья – 1 %. Найти вероятность, что купим не бракованную.

12.   В ящике лежат 9 шаров: 2 белых, 3 красных и 4 зеленых. Берут один шар. Какова вероятность, что окажется цветной ( не белый). (Округлить до сотых).

13.  В колоде 36 карт. Вынимают одну карту. Какова вероятность, что это валет, дама или король. (Округлить до тысячных).

Произведение  вероятностей.

1.      На запись в первый класс пришли два будущих первоклассника с мамами. Считая, что приход мальчика и девочки равновероятны, найти вероятность того, что это обе девочки.

2.      В магазине три продавца, каждый из них занят с покупателем с вероятностью 0,6. Найти вероятность, что все три заняты одновременно.

3.      Если А. играет белыми, то он выигрывает у Б. с вероятностью 0,52. Если А. играет черными, то выигрывает у Б. с вероятностью 0,2. Они играют две партии, во второй меняют цвет фигур. Найти вероятность, что А. выиграет оба раза.

4.      Две лампы. Вероятность, что перегорит одна  равна 0,3. Какова вероятность, что хотя бы одна не перегорит.

5.      Вероятность, что ученик сдаст ЕГЭ по русскому равна 0,9, что сдаст по математике  0,7. Найти вероятность, что     а) сдаст и по одному и по другому;

б) не сдаст математику, а сдаст русский язык;

в) не сдаст оба экзамена.

 6.  Биатлонист стреляет по мишени 3 раза. Вероятность, что он попадет равна 0,8. Найти     вероятность, что он 2 раза попадет, 1 раз промахнется.

7.Биатлонист стреляет по мишени 5 раза. Вероятность, что он попадет равна 0,9. Найти  вероятность, что он  3 раза попадет, а два раза промахнется. (Результат округлить до тысячных).

8.Некоторый прибор состоит из трех блоков. Вероятность сбоя первого равна 0,3, второго 0.1, третьего 0,4. Какова вероятность, что в течение не произойдет сбоя ни одного блока.

9. Вероятность, что батарейка бракованная равна 0,06. Покупатель выбирает упаковку, где две батарейки.  Найти вероятность, что обе будут исправны.

10  Оля отдыхает в санатории S. Она хочет  купить яблок. Какова вероятность, что она купит яблоки. Яблоки продаются в  павильонах:  а) В и С;  б) только в павильоне В.

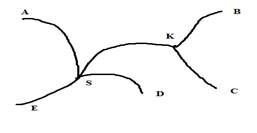
11. Пенсионер гуляет по дорожкам парка. Проходя по дорожкам, он нигде не возвращается назад. Найти вероятность, что выйдя из точки А, он придет:   а) в точку К;   б) в точку D.

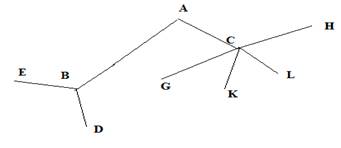
12. Лабиринт. Паук заползает через вход. Вернуться или ползти назад он не может.

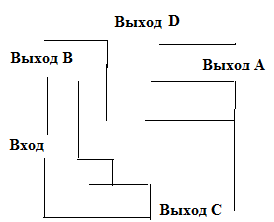
Найти вероятность, что он придет к выходу  D.

13.Бросают два кубика. Найти вероятность, что выпадет по 5 очков на каждом.(Округлить до десятых).

14.Таня отправляет СМС. Вероятность успешной отправки с одного раза равна 0,8. Какова вероятность, что СМС удалось отправить с третьей попытки.

15. В торговом центре установлены два платежных автомата. Каждый может быть неисправен с вероятностью 0,05. Найти вероятность, что хотя бы один автомат исправен.

16.Вероятность, что товар доставят из магазина А равна 0,81, что доставят из магазина Б равна 0,93. Найти вероятность, товар не доставят.

17.Чтобы пройти в следующий круг соревнований команде надо набрать хотя бы 4 очка в двух играх. Если она выигрывает, то получает 3 очка, ничья – 1 очко, проигрывает – 0 очков. Вероятность выигрыша и проигрыша одинакова и равна 0,4. Найти вероятность, что команда выйдет в следующий круг.

18.При артобстреле система делает выстрел по цели. Если цель не уничтожена, то повторяют выстрел, пока не уничтожат. Вероятность уничтожения при первом выстреле равна 0,4, при каждом следующим 0,6. Сколько надо сделать выстрелов, чтобы вероятность поразить цель была не менее 0,98 ( наименьшее количество выстрелов).

19.При стрельбе система делает выстрел по цели. Если цель не уничтожена, то повторяют выстрел, пока не уничтожат. Вероятность уничтожения при первом выстреле равна 0,3,при каждом следующим 0,9. Сколько надо сделать выстрелов, чтобы вероятность поразить цель была не менее 0,96.

20.В некоторой области утро в мае бывает либо ясным, либо облачным. Если ясное, то вероятность дождя равна 0,2, если облачно, то вероятность дождя 0,6. Вероятность, что утро облачно равна 0,4. Найти вероятность, что дождя не будет.

21.Чтобы поступить на «Лингвистику» надо набрать не менее 70 баллов по каждому из трех предметов: математика, русский язык, иностранный язык. Чтобы поступить на специальность «Коммерция» надо набрать не менее 70 баллов по каждому из трех предметов: математика, русский язык, обществознание. Вероятность, что ученик получит не менее 70 баллов по математике равна 0,6, по русскому 0,8, по иностранному языку 0,7, по обществознанию 0,5. Найти вероятность, что ученик поступит хотя бы на одну из этих специальностей.

22. Два стрелка стреляют по мишени. Первый попадает с вероятностью 0,9 , второй с вероятностью 0,8.Какова вероятность, что  а) оба попали;  б) первый попал, а второй промахнулся; в) оба промахнулись.

23. Вероятность остановки за смену одного станка равна 0,15, второго 0,16. Какова вероятность, что   а) оба не остановятся; б)  оба остановятся;  в) не остановится хотя бы один;     г ) остановится хотя бы один?

Сумма и произведение  

1.      В торговом центре кофе продается в двух автоматах. Вероятность, что кофе закончится в одном равна0,3. Что закончится в обоих равна 0,12. Найти вероятность, что кофе останется в обоих автоматах.

2.      Две фабрики выпускают стекла для фар. Первая выпускает 45 %этих стекол, а вторая 55%. У первой бывает 3% брака, а у второй только 1 % брака. Найти вероятность, что при покупке попадется бракованная  фара.

3.      Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристреленного револьвера. Если стреляет из не пристреленного, то попадает с вероятностью 0,2. На столе 10 револьверов, из них 4 пристреленных. Найти вероятность, что он промахнется.

4.      Агрофирма закупает яйца в двух хозяйствах. 40% из первого хозяйства – это яйца высшей категории, а из второго хозяйства 20% - высшей категории. Всего высшую категорию получают 35%  яиц. Найти вероятность, что купим из первого хозяйства.

5.      Петя подбросил три монеты. С какой вероятность., они упадут одной стороной?

6.      Стрелок стреляет по мишени один раз,   в случае промаха делает второй выстрел. Вероятность попасть при одном выстреле 0,6. Найти вероятность, что мишень будет поражена одним выстрелом.                      Разные задачи.

7.      При изготовлении подшипников диаметром 69мм вероятность, что диаметр отличается от заданного не более чем на 0,01 мм равна 0,975. Найти вероятность, что диаметр будет меньше 68,99 мм или больше 69,01 мм.

8.      Оля написала трехзначное число, делящееся на 28. Витя должен отгадать, написав 6 трехзначных чисел, которые делятся на 28. Найти вероятность, что он отгадает.

9.      Маша написала трехзначное число, делящееся на 36. Саша должен отгадать, написав 6 трехзначных чисел, которые делятся на 36. Найти вероятность, что он отгадает.

                                                        Ответы на задания.

Сумма вероятностей.

1.      0,73                2.     0,4                3.  0,3            4.   0,12            5.     0,53

6.       0,11         7.   0,58              8.     0,7               9.    0,38         10.  0,034      

  11.     0,9615      12.  0,78       13. 0,333.

                                             Произведение  вероятностей.

1.        0,25              2.   0,216                    3.   0,156                                   4.   0,91  

 5. а)   0,63    б) 0,27   в) 0,03               6. 0,128          7.  0,007            8.   0,378

9.  0,8836       10.   а) 0,25   б)  0,125     11.   а) 0,125     б) 0,25       12.  0,0625

13.  0,3          14.  0,032          15.  0,9975          16. 0,0133     17.  0,32       18.  5     19.   3 (а получается 4) 20.   0,64    21.   0,408   22.  а) 0,72;  б) 0,18;   в) 0,02.

23.  а) 0,714;   б) 0,024;   в)  0,286    г)  0,976.

                                   Сумма и произведение вероятностей.

1.     0,52          2.   0,019              3.  0,52                4.   0,75           5. 0,25

6.      0,84    

Разные задачи

 7.   0,025             8.  0,1875             9.    0,24