Поделиться
СР по теме Равнобедренный треугольник и окружность.docx
Самостоятельная работа
Вариант 1.
1. Сформулируйте ответ на вопросы:
а) Что такое треугольник?
б) Что такое хорда?
в) Что такое медиана?
2. Решите задачу на доказательство:
В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. ВD – медиана треугольника. Докажите, что ∆ BKD = ∆ BMD.
3. Решите задачу:
В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2. Найдите стороны треугольника.
4.
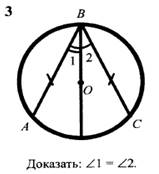
Самостоятельная работа
Вариант 2.
1. Сформулируйте ответ на вопросы:
а) Что такое равнобедренный треугольник?
б) Что такое диаметр?
в) Что такое биссектриса?
2. Решите задачу на доказательство:
В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. ВD – медиана треугольника. Докажите, что ∆ AKD = ∆ CDM.
3. Решите задачу:
В равнобедренном треугольнике с периметром 56 см боковая сторона относится к основанию как 3 : 8. Найдите стороны треугольника.
4.
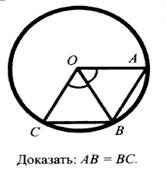
Самостоятельная работа
Вариант 1.
1. Сформулируйте ответ на вопросы:
а) Что такое треугольник?
б) Что такое хорда?
в) Что такое медиана?
2. Решите задачу на доказательство:
В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. ВD – медиана треугольника. Докажите, что ∆ BKD = ∆ BMD.
3. Решите задачу:
В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2. Найдите стороны треугольника.
4.
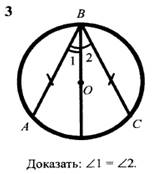
Самостоятельная работа
Вариант 2.
1. Сформулируйте ответ на вопросы:
а) Что такое равнобедренный треугольник?
б) Что такое диаметр?
в) Что такое биссектриса?
2. Решите задачу на доказательство:
В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. ВD – медиана треугольника. Докажите, что ∆ AKD = ∆ CDM.
3. Решите задачу:
В равнобедренном треугольнике с периметром 56 см боковая сторона относится к основанию как 3 : 8. Найдите стороны треугольника.
4.
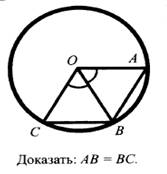
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
