Самостоятельная работа с заданиями по геометрии для подготовки к ОГЭ

Самостоятельная работа по геометрии

Вариант № 1

1. Задание 15 

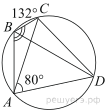
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 132°, угол CAD равен 80°. Найдите угол ABD. Ответ дайте в градусах.

2. Задание 15 

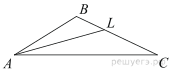
В треугольнике ABC проведена биссектриса AL, угол ALC равен 121°, угол ABC равен 101°. Найдите угол ACB. Ответ дайте в градусах.

3. Задание 15 №

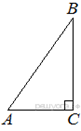В треугольнике  известно, что , , угол  равен 90°. Найдите радиус описанной окружности этого треугольника.

4. Задание 15 

В треугольнике два угла равны 31° и 94°. Найдите его третий угол. Ответ дайте в градусах.

5. Задание 18 

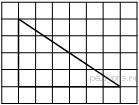На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.

6. Задание 18 

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

7. Задание 19 

Какие из данных утверждений верны? Запишите их номера.

1) Вокруг любого треугольника можно описать окружность.

2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

3) Площадь трапеции равна произведению средней линии на высоту.

Если утверждений несколько, запишите их номера в порядке возрастания.

Вариант № 2

1. Задание 15 

В треугольнике ABC угол C равен 90 °, BC = 6, sin A = 0,3. Найдите AB.

2. Задание 15 

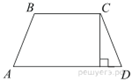
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 19. Найдите длину основания BC.

3. Задание 15 

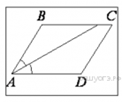
Найдите величину острого угла параллелограмма , если биссектриса угла  образует со стороной  угол, равный 43°. Ответ дайте в градусах.

4. Задание 15 

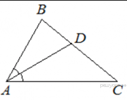
В треугольнике  известно, что ,  - биссектриса. Найдите угол . Ответ дайте в градусах.

5. Задание 18 

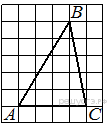На клетчатой бумаге с размером клетки 1х1 изображён треугольник . Найдите длину его средней линии, параллельной стороне .

6. Задание 18 

Найдите тангенс острого угла, изображённого на рисунке.

7. Задание 19 

Какие из следующих утверждений верны?

1) Каждая сторона треугольника меньше разности двух других сторон.

2) В равнобедренном треугольнике имеется не более двух равных углов.

3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.

4) В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.

Вариант № 3

1. Задание 15 

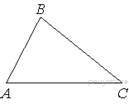
В треугольнике ABC известно, что    Найдите площадь треугольника ABC.

2. Задание 15 

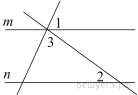
Прямые m и n параллельны. Найдите ∠3, если ∠1 = 59°, ∠2 = 38°. Ответ дайте в градусах.

3. Задание 15 

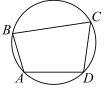Угол A четырёхугольника ABCD, вписанного в окружность, равен 56°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

4. Задание 15 

Площадь прямоугольного треугольника равна  Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.

5. Задание 18 

Найдите тангенс угла , изображённого на рисунке.

6. Задание 18 

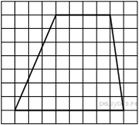На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

7. Задание 19 

Какие из данных утверждений верны? Запишите их номера.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.

В ответ запишите номер выбранного утверждения.

Вариант № 4

1. Задание 15

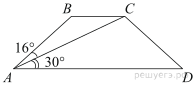
Найдите больший угол равнобедренной трапеции , если диагональ  образует с основанием  и боковой стороной  углы, равные 30° и 16° соответственно. Ответ дайте в градусах.

2. Задание 15 

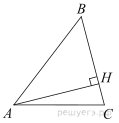
В остроугольном треугольнике ABC высота AH равна 42 а сторона AB равна 70. Найдите cosB.

3. Задание 15 

Площадь прямоугольного треугольника равна  Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.

4. Задание 15 

В треугольнике  угол  равен 90°, , . Найдите .

5. Задание 18

Найдите угол . Ответ дайте в градусах.

6. Задание 18 

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

7. Задание 19 

Какое из следующих утверждений верно?

1. Все квадраты имеют равные площади.

2. Основания равнобедренной трапеции равны.

3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

Ответы

Вариант № 1

1. Задание Ответ: 52

2. Задание Ответ: 39

3. Задание Ответ: 12,5

4. Задание Ответ: 55

5. Задание Ответ: 6

6. Задание Ответ: 5

7. Задание Ответ: 123

Вариант № 2

1. Задание Ответ: 20

2. Задание Ответ: 18

3. Задание Ответ: 86

4. Задание Ответ: 42

5. Задание Ответ: 2

6. Задание Ответ: 2

7. Задание Ответ 4

Вариант № 3

1. Задание Ответ: 10

2. Задание Ответ: 83

3. Задание Ответ: 124

4. Задание Ответ: 18

5. Задание Ответ: 1,5

6. Задание Ответ: 42

7. Задание Ответ: 13|31

Вариант №4

1. Задание Ответ: 134

2. Задание Ответ: 0,8

3. Задание Ответ: 12

4. Задание Ответ: 2

5. Задание Ответ: 45

6. Задание Ответ: 4

7. Задание Ответ: 3