Самостоятельная работа "Угол прямой с плоскостью" . Геометрия 10 класс.

Самостоятельная работа.

Тема: «Угол между прямой и плоскостью».

Вариант 1.

1.     Ответить на вопросы по рисунку

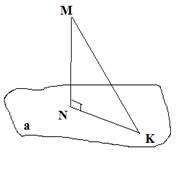
Как называется     1) отрезок    MK;   2) отрезок    MN; 3)  отрезок    KN;

4) точка  К;      5) точка N.

2. Решите задачи.

Задача 1.  Из некоторой точки проведены к плоскости перпендикуляр и наклонная. Длина перпендикуляра равна 8 см, длина наклонной равна 17 см. Найдите длину проекции Задача 2.  Из некоторой точки проведены к плоскости перпендикуляр и наклонная. Длина  наклонной равна 26, угол, который наклонная образует с плоскостью, равен 60°. Найдите длину проекции наклонной на эту плоскость.                                                  Задача 3.  Из некоторой точки проведены к плоскости перпендикуляр и две наклонные, которые образуют с перпендикуляром углы 60° и 30° соответственно. Длина перпендикуляра равна 12√3, угол между проекциями наклонных на плоскости равен 90°. Найдите  расстояние между основаниями наклонных. ( Результат округлить до целого). Задача 4.   Точки А и В расположены по одну сторону от плоскости α. Отрезки АС и ВD – перпендикуляры, проведенные из точек А и В к плоскости α. АС = 3,  ВD = 2,  СD = 2,4. Найдите  АВ.

Задача 5.    Из некоторой точки проведены к плоскости перпендикуляр и наклонная. Наклонная составляет с плоскостью угол 45°. Проекция наклонной на плоскость равна 5√2. Найдите  а) длину перпендикуляра;  б) длину наклонной.

Задача 6.    Из некоторой точки проведены к плоскости перпендикуляр и две наклонные, Наклонные образуют между собой угол, равный 90°. Длина одной наклонной равна 24, длина другой наклонной равна 10. Найдите расстояние между основаниями этих наклонных на плоскости.

Самостоятельная работа.

Тема: «Угол между прямой и плоскостью».

Вариант 2.

2.     Ответить на вопросы по рисунку

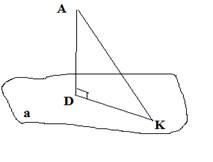Как называется     1) отрезок    AK;   2) отрезок    AD; 3)  отрезок    KD;

4) точка  К;      5) точка D.

2. Решите задачи.

Задача 1.  Из некоторой  точки проведены к плоскости перпендикуляр и наклонная. Длина  наклонной равна 15 см, длина проекции наклонной на эту плоскость равна 9 см. Найдите длину перпендикуляра.

Задача 2.  Из некоторой точки проведены к плоскости перпендикуляр и две наклонные, которые образуют с плоскостью углы 60° и 30° соответственно. Длина перпендикуляра равна 10√3, угол между проекциями наклонных на плоскости равен 90°. Найдите  расстояние между основаниями наклонных. ( Результат округлить до целого).

Задача 3.  Точки С и К расположены по одну сторону от плоскости α. Отрезки СD  и KM – перпендикуляры, проведенные из точек C и K к плоскости α. DM = 15,  CD = 18, 

KM = 10. Найдите  CK

 Задача 4.  Из некоторой точки проведены к плоскости перпендикуляр и наклонная. Наклонная составляет с перпендикуляром угол 45°. Длина перпендикуляра равна 4√2. Найдите  а) длину проекции наклонной;  б) длину наклонной.

Задача 5.  Из некоторой точки проведены к плоскости перпендикуляр и наклонная. Длина  наклонной равна 8√3, угол, который наклонная образует с плоскостью, равен 30°. Найдите длину проекции наклонной на эту плоскость. 

  Задача 6.       Из некоторой точки проведены к плоскости перпендикуляр и две наклонные, Наклонные образуют между собой угол, равный 90°. Длина одной наклонной равна 24, длина другой наклонной равна 52. Найдите расстояние между основаниями этих наклонных на плоскости.

Ответы на задачи.