Поделиться
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.docx
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Скаляр- это есть числа.
Определение. Скалярным произведением на 
и 
называеться число равное
произведению этих векторов на cos
угла между векторами 
и 
.
* 
)- обозначение скалярного
произведения.
( 
, 
* cos (
Основные свойства скалярного произведения.
10.
Если 
скалярно умножается на 
( 
, 
– коммутативность.
( 
, 
=
.
Ничего не меняется.
20. Для любого числа λ.
)= ( 
,λ 
(3 
, 
а) λ>0 тогда
(λ
,
)=
=
(λ 
, 
)=
b) λ<0
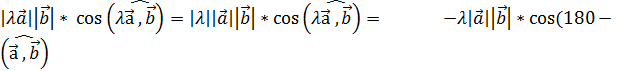(λ 
, 
)=
)=
=λ
30. (
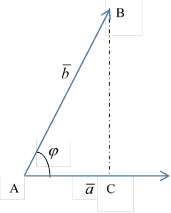∆OCB-⊥-ый
Проекция вектора 
по направлению вектора 
(
– проекция)
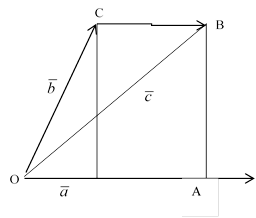OK=
KM= 
OM=
=
(
OM=OK+KM
(
(
+
)=
(
+
)=
=(
=
)+(
40. 
,
)=0
1) 
=0
2) 
=0
3)
(
)=900 т.е.
,
=
(
,
)=
cos
=0
(
,
cos
=0
,
=
cos 900=0
(
) =
cos 
=
2
(
) =
2
- формула определения длины вектора
(
)=
cos 
(
)=
Cкалярное произведение в координатах вектора
Пусть задан прямоугольно декартовый ортонормированный базис I, j в двумерном векторном подпространстве вектора v2.
Пусть дана относительно этого базиса вектор 
Задача данного параграфа заключается в том чтобы вычислить скалярное произведение этих векторов с помощью этих координат.
(
, 
) =
cos 00= 1
( 
, 
)= 
0= 1
( 
, 
)= 
cos 900 = 0
( 
, 
)= 0
= x1
+ y1
,
= x2
+ y2
(
) = (x1
+ y1
, x2
+ y2
) = (x1
, x2
) + (x1
, y2
) + (y1
, x2
) + (y2
+ y2
) = x1x2
(
, 
) + x1y2
( 
, 
) + y1x2
(
, 
) + y1y2
( 
, 
) = x1x2 +
y1y2 .
 |
(
) = x1x2
+ y1y2
ПРИМЕР:
, 
(
) = -14 + 20 = 6 (
) = 6
Можно определить и угол между векторами зная их координаты.
Cos (
) = 
Тогда:
Cos (
) = 
Учитель математики ГКОУ РД «РЦДОДИ» Гаджимирзаев М.М.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
