Сборник задач для отработки материала по теме "Многогранники"

1.Таблица.

Строим такую же в тетради, заполняем все колонки.

2. Тест

В тетради записываем только ответы. Пожалуйста, оформите это задание в столбик.

1. Поверхность, составленная из четырех треугольников

А) тетраэдр

B) параллелепипед

С) квадрат

D) шар

2. Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело

А) многоугольник

B) многогранник

С) треугольник

D) квадрат

3. Многоугольник, из которого составлен многогранник

А) сторона

B) ребро

С) грань

D) вершина

4. Отрезок, соединяющий две вершины, не принадлежащие одной грани

А) диагональ

B) медиана

С) высота

D) апофема

5. Высота боковой грани правильной пирамиды, проведенная из ее вершины

А) диагональ

B) апофема

С) катет

D) гипотенуза

6. Этот правильный многогранник составлен из 8-ми равносторонних треугольников

А) квадрат

B) тетраэдр

С) додекаэдр

D) октаэдр

7. Составлен из 6-ти правильных четырехугольников

А) квадрат

B) тетраэдр

С) куб

D) пирамида

8. Стихия тетраэдра

А) вода

B) воздух

С) земля

D) огонь

9. Многоугольник, подобный пчелиным сотам

А) 8-ми угольник

B) 6-ти угольник

B) 6-ти угольник

D) треугольник

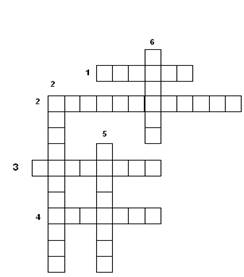
3. Кроссворд.

Перерисовывать кроссворд не нужно, только ответы.

Пишем: по горизонтали, №1-…, №2-…

По горизонтали:
1. Количество сходящихся ребер у октаэдра.

2. Грань додекаэдра.

3. Боковая грань усеченной пирамиды.

4. Правильный многогранник.

По вертикали:
2. Граница многогранника.

5. Правильная треугольная пирамида.

6. Перпендикуляр, опущенный из вершины

пирамиды на плоскость основания.

Задачи.

Оформляем себе в тетрадь, рисунки тоже переносим.

№1.  Найдите высоту правильного тетраэдра с ребром 10 см.

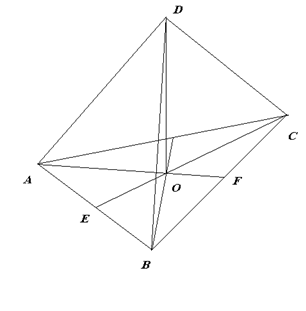
Дано:  ABCД – правильный тетраэдр, 

AВ=10 см

Найти: высоту тетраэдра

Решение.

 1)  AF –   медиана    _ΔABС, значит ВF = ______

2) Из   _ΔABF по теореме  _______  найдем АF

AF²=AB²- BF²

AF=________

3) О делит отрезок AF в отношении 2:1, поэтому АО=_____________________

4) Из   _ΔADO по теореме  Пифагора  найдем DO

DO²=____________

DO = ____________

Ответ: ______см

№2. Решите задачу, используя план решения

Кристалл имеет форму октаэдра, состоящего из двух правильных пирамид с общим основанием,  ребро основания пирамиды  6 см. Высота октаэдра 14 см. Найдите площадь боковой поверхности кристалла.

 Решение.

1)  S_бок = 2 S_пир = p∙• SK (где SK – апофема, p – полупериметр ABCD)

2) Находим ОК _________________________

 ______________________________________

3) Находим SO ________________________

______________________________________

4) Находим SK ________________________

______________________________________

5) Вычисляем S_{бок __________________________________}

______________________________________

Ответ:

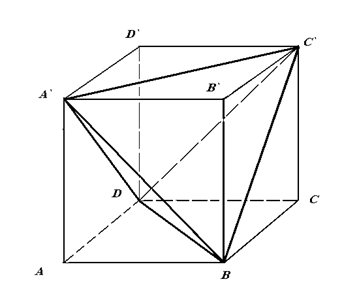
№3.   Докажите, что концы двух непараллельных диагоналей противолежащих граней куба являются вершинами тетраэдра.