Сборник задач и упражнений по учебной дисциплине «МАТЕМАТИКА»

 

 

 

 

 

 

 

С Б О Р Н И К

 

задач и упражнений по учебной дисциплине

«МАТЕМАТИКА»

для обучающихся по профессии: «Электромонтер устройств сигнализации, централизации и блокировки»

 

( учебно - методическое пособие)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 ИБРАГИМОВА АНИФЕ РИШАТОВНА

преподаватель математики   высшей квалификационной

категории

КФ ГБПОУ РК «Джанкойский

профессиональный техникум».

 

 

 

Настоящее методическое пособие является методическим руководством для подготовки квалифицированных работников сельскохозяйственного профиля.

В сборник включены: краткий курс лекции, освещающий все вопросы, вынесенные на тематическое оценивание; тренинг умений; задачи и упражнения по алгебре и начала математического анализа; материалы, необходимые для подготовки и успешной сдачи тематического оценивания.

Цель сборника - научить обучающихся свободно владеть методикой решения задач по курсу «Алгебра и начала математического анализа» изучающей массовые явления в электротехнике.

Сборник предназначен для обучающихся по специальности «Электромонтер устройств сигнализации, централизации и блокировки.

 

 

 

 

 

 

 

 

 

 

П Р Е Д И С Л О В И Е

 

Предлагаемый обучающимся и преподавателям сборник задач представляет собой дополнительное пособие, которое должно способствовать установлению связей между математикой как учебным предметом и ее приложением по дисциплине «Электромонтер устройств сигнализации, централизации и блокировки».

Комментарии, которыми снабжены условия и решения задач, должны помочь обучающимся разобраться как в математической стороне рассматриваемых ситуаций, так и в той роли, которую предлагаемые методы играют в практических приложениях. В сборник включены также задачи по экономике сельскохозяйственного производства.

В соответствие с программой для средней школы в пособие входят задачи по алгебре и начала математического анализа.

В каждом разделе имеется теория, тренинг умений, задания и вопросы тематического оценивания. Задачи имеют производственное содержание. В отдельные задачи введена профессиональная терминология, тем не менее, их математическая сущность достаточно ясна. Раскрывается сущность используемых при решении задач производственных категорий.

 

 

 

 

В В Е Д Е Н И Е

 

Важнейшая роль математики в общеобразовательном фундаменте профессиональной подготовки современного молодого рабочего особенно ярко проявляется в настоящее время.

Современный квалифицированный рабочий должен хорошо представлять положение своего рабочего места, участка в деятельности всего цеха, предприятие, за повышение эффективности и качества работы. Квалифицированный рабочий должен непрерывно совершенствовать профессиональные навыки и умения, развивать в себе способность изменять характер и содержание трудовых функций в изменяющейся производственной ситуации, творчески применять полученные во время обучения в техникуме и самостоятельно приобретенные знания, активно участвовать в рационализаторской деятельности, повышать культуру труда, которая требует и определенной культуры мышления. И здесь будущим молодым рабочим существенно поможет знание математических методов и умение применять их в своей деятельности. Рабочему нужно уметь подставить числовые данные в формулу, построить график, осмыслить и проконтролировать полученный результат. Такое освоение и применение математики дисциплинирует ум, вносит элементы порядка, оказывается полезным при изучении других наук. И если ограничиться этим, то теория усваивается пассивно. В лучшем случае активность обучающихся будет направлена на установление порядка в знаниях, а не на установление порядка в деятельности. В результате знания забудутся. Конечно, знания по математике будут низкими.

Важнейшую роль в сборнике играют формулы. Отыскание формулы - это раскрытие характера общей зависимости между рассматриваемыми величинами.

Данный сборник как задачник по прикладной математике - использование большого разнообразия ситуаций электротехники.

Об использовании сборника необходимо сказать лишь то, что, когда обучающийся самостоятельно получит решение задачи, ему полезно ознакомиться и с авторским. Но для активного режима учебной работы обучающимся рекомендуется воздерживаться от желания заглянуть в ответы до тех пор, пока они сами не вникли в условие задачи, не поработали над ним, не попытались найти собственный путь решения.

 

 

1.                    Проценты.

1.1.          Выделение групп задач на проценты

При сортировке задач на проценты, можно выделить 3 основные группы: 

- обычные задачи на проценты (повседневные, вычисления процентов от числа);

        -  задачи на смеси, растворы, сплавы; 

        - задачи банковских систем (кредиты, вклады).

Обычные задачи на проценты (повседневные).

В этот вид задач входят все задачи, начиная с простого вычисления процента от числа и заканчивая самыми разнообразными ситуациями нашей жизни, требующих вмешательство процентов.

Задачи на смеси, растворы, сплавы.

Данный тип задач охватывает большой круг ситуаций — смешение товаров разной цены, жидкостей с различным содержанием соли, кислот различной концентрации, сплавление металлов с различным содержанием некоторого металла и пр. Лучше всего для таких задач подходит формула:

n_k = m_в : m_Р; где n — концентрация, m_в - масса вещества в растворе, m_Р -масса всего раствора.

Задачи банковских систем.

Задачи банковских систем — задачи, связанные с начислениями процентов в банке по вкладам и кредитам. Такие задачи обычно решаются по двум формулам:

1.   Sn=S₀ * (1 + рn: 100) -(формула простых процентов, где S_n – наращенная сумма (исходная сумма вместе с начисленными процентами, S₀ – исходная сумма, р% – процентная ставка от суммы, выраженная в долях за период; а n – число периодов начисления).

2.   S_n=S_{0 *} (l + p: 100) ⁿ -(формула сложных процентов).

S_n - полученная сумма; S₀ - начальная сумма; n — кол-во лет,

 где n = 1, 2,3...

           Основные формулы для вычисления процентов:

              1% − это 1 часть от целого. Если а − 100%, b − р%, то

              100

·      Процент от числа b =  

                                     

·      Число по проценту а =                                               

·         Количество процентов, которое составляет число b от числа а  

p =            

Решение любых задач на проценты сводится к основным трём формулам или действиям с процентами.

 

 

Соотношения, которые полезно запомнить:

50% числа х – это его половина (0,5х или х)

25% числа х – это его четверть (0,25х или х)       

20% числа х – это его пятая часть (0,2х или х)

75% числа х – это его три четверти ( 0,75х или х)

100% числа х – это всё число х.  

   

               2.1. Обычные задачи на проценты

         

1.Цена изделия составляла 1000 р. И была снижена сначала на 10 %, а затем еще на 20%. Какова окончательная цена товара?

Подобные задачи удобно решать с помощью такой схемы рассуждений:

                                   -  -10%                         -20%

                           

                      -100р                          -180р

        

Первое снижение цены товара было на 0,1*1000 = 100р. После первого снижения цена товара составила 1000-100 = 900р. Второе снижение цены товара было на 0,2*900 = 180 р. После второго снижения цена товара составила 900 – 180 = 720 р.

Ответ: 720 р.

 

2.Цену товара повысили на 25%, затем новую цену повысили еще на 10% и, наконец, после перерасчета произвели повышение цены еще на 12%. На сколько процентов повысили первоначальную цену товара?

         Обозначим первоначальную цену товара за х (р.),   тогда после первого повышения цена товара стала 1,25%. Второе повышение цены было на 0,1*1,25х. После него цена товара стала 1,25х + 0,1*1,25х = 1,375х. Третье повышение цены на 12% производилось от цены, полученной после второго повышения, и составило 0,12*1,375х = 0,165х. После последнего повышения цена товара составила 1,375х + 0,165х = 1,54х.

Схема рассуждений была следующей:

                      +25%               +10%                  +12%

                                       

     +0,25х            +0,125х              +0,165х

 

     2.2. Задачи на смеси, растворы, сплавы.

      1) Имеются два куска сплава меди и цинка с         процентным содержанием меди 42% и 65% соответственно. В каком отношении нужно взять эти сплавы, чтобы, переплавив, получить сплав, содержащий 50% меди?

       Изобразим схематически условие задачи:

            +        +                

Количество меди в каждом сплаве найдено с помощью соотношения между величинами. Можем составить уравнение: 0,42х + 0,65у = 0,5(х+у).

В этом уравнении две неизвестных, а в задаче требуется найти их соотношение       

Решая уравнение, получим 42х + 65у = 50 ( х +у),

 15у = 8х, х: у = 15:2.

Ответ: нужно взять первый и второй сплавы в отношении         

       

2) Имеется два сплава с разным содержанием железа: в первом содержится 75 %, а во втором – 25 % железа. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40 % железа?

Решение:

Пусть x и y – количество первого и второго сплава соответственно (x > 0; y > 0)

Тогда концентрация железа в новом сплаве составит

 

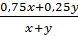 =0,4

 

0.35 x = 0.15 y

 =

 

Ответ:     

2.3. Задачи банковских систем и сложных процентов.

 

1)    Сколько надо заплатить, если платёж 5000 р. Просрочен, пеня равна 1 % за каждый день просрочки, а оплата производится с задержкой на 5 дней?

Подставляем в формулу простого процентного роста

 

S_n=(1+)s

 

S_n=(1+)*5000

   

S_n = 5250

     

Ответ: 5250 р.

 

2)    Клиент внёс 3000 рублей на 2 вклада, один из которых даёт годовой доход, равный 8%, а другой – 10 %. Через год на 2х счетах у него было 3260 рублей. Какую сумму клиент внёс на каждый вклад?

Пусть х – 1-ый вклад, у – 2-ой вклад.

Тогда 108% – 1-ый вклад, 110 % – 2-ой вклад.

Значит, х+ у = 3000, а 1,08х+1,1у=3260.

Получаем систему:

х+ у = 3000

1,08х+1,1у=3260

Выражаем х = 3000 – у

1,08*(3000-у)+1,1у = 3260

3240 –1, 08у +1,1у = 3260

0,02у = 20

 у = 2000

х = 1000

Ответ: 1000 и 2000 рублей.

Повторение:

Сотая часть числа называется процентом.

Нахождение процентов данного числа.

Чтобы найти несколько процентов данного числа, надо процентную запись числа заменить записью этого числа в виде дроби, затем данное число умножить на эту дробь.

Например: Найти 7,2 % от 860.

7,2% = 0,072

860∙0,072 = 61,92

Нахождение числа по его проценту.

Чтобы найти число по его процентам, надо процентную запись числа заменить дробью, а затем данную часть искомого числа разделить на полученную дробь.

Задача. В первый день рабочий выполнил 35 % всего задания, во второй день- 60 % от того, что сделал в первый день, а в третий день- всю оставшуюся часть задания. Во второй день рабочий изготовил на 184 детали меньше, чем в третий день. Сколько деталей изготовил рабочий за три дня?

Решение. В первый день рабочий выполнил 35 % всего задания. Во второй- 60 %, от числа деталей, изготовленных в первый день. Найдем

60 % от 35 %, т.е. 0,6 от 0,35.

0,6∙0,35 = 0,21= 21 %

За два первых дня рабочий выполнил

35 % + 21 % = 56 % всего задания. В третий день он выполнил 100% -56 % = 44 % всего задания.

Теперь найдем, на сколько процентов задания больше было сделано, в третий день, чем во второй. 44 % - 21 % = 23 %.

Но по условию в третий день было изготовлено на 184 детали больше, чем во второй день. Следовательно, 184 детали составляют 23 %, или 0,23 всего задания. Наконец, можно ответить на главный вопрос задачи – определить все задания. Имеем, 184*0,23 = 800.

Итак, задание на все три дня составляло 800 деталей.

Нахождение процентного отношения двух чисел.

Задача. Бригаде электриков была установлена норма-протягивание электропровода по 2,5 км. В день. В первый день бригада протянула 2 км. Провода, во второй день 3 км. Найти процент выполнения нормы в первый день и во второй день.

Решение. Для решения задачи найдем отношения чисел 2 к 2,5 и 3 к 2,5 и выразим их в процентах.

 = 0,8= 80%          = 1,2= 120%

Следовательно, в первый день задание было выполнено на 80 %, а во второй- на 120 %.

Формула простых процентов S=P (1+n i), где P- первоначальный вклад, i-    процентная ставка                  

 (десятичная дробь), S – суммарная величина вклада в конце n-го периода, величина ( 1+ n i)- множитель наращения простых процентов.

Тренинг умений

Задача. Первый рабочий производит продукцию на одну копейку в течении одной секунды. Второй – на один рубль за одну минуту. Во сколько раз производительность второго рабочего больше первого?

Решение:

Под производительностью труда понимаем стоимость продукции, изготовленной рабочим за единицу времени. Поэтому производительность первого рабочего равна 1 коп/с. Производительность второго рабочего, выражена в тех же единицах измерения, равна 100 коп/60 с. Поделив одно на другое получим ответ 5/3.

Задача. В цехе работают 20 рабочих, из них 8 электриков. Сколько процентов    от всего числа рабочих составляют электрики?

Решение: 20  -  100 %

                   8   -   x %

 

х= ;         х= 40 %

Задача. Зарплата электрика составляла 10000 руб. Затем её повысили на 20 %, а вскоре понизили на 20 %. Сколько стал получать электрик?

Решение: 10000 – 100%

                      х - 20%

 

x=;   х=2000 руб

    

12000 – 100%

х – 20%

х=;   х=2400

 

2400-1000=1400 руб

10000-1400=8600

Задачи и упражнения для самопроверки.

1.1. Цену товара сначала снизили на 20 %, затем новую цену снизили еще на 15 % и, наконец, после перерасчета произвели снижение еще на 10 %. На сколько процентов всего снизили первоначальную цену товара?

1.2. Рабочий день электрика уменьшился с 8 до 7 ч. На сколько процентов нужно повысить производительность труда, чтобы при тех же расценках заработная плата возросла на 5 %?

1.3.В январе завод выполнил 105 % месячного плана выпуска готовой продукции, а в феврале дал продукции на 4 % больше, чем в январе. На сколько процентов завод перевыполнил двухмесячный план выпуска продукции?

1.4. На монтаж прибора уходило 225 м. провода. После внедрения новой схемы монтажа на этот же прибор стали расходовать 198 м. провода. На сколько процентов уменьшилась затрата провода?

 

2. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫ УРАВНЕНИЙ.

2.1.     ФУНКЦИИ.

Переменная у является функцией от переменной х, если задана такая зависимость между этими переменными, которая позволяет для каждого, значения х однозначно определить значение у.

Для того чтобы задать функцию, нужно:

1)                   указать множество всех возможных значений переменной х.

Это множество, которое мы будем обозначать D, называют

областью определения функции;

2)                   указать правило, по которому каждому числу х из множества D

сопоставляется число у, определяемое числом х. Это число у называется

значением функции в точке х. Переменную х называют аргументом.

Графиком функции f называется множество точек плоскости с координатами (x; f (x)), где х пробегает область определения функции f.

Функция f, у которой для всех х из ее области определения f(-x) = f(x) называется четной.

Функция f, у которой для всех х из ее области определения f(-x) = -f(x) называется нечетной.

Функция у = f(x), для которой большему значению аргумента из (а, в) соответствует большее (меньшее) значении функции, т.е. для х <  x следует f(x)<f(x),

( f(x) > f(x) ) называется функция монотонно возрастающей (убывающей) на интервале (а, в).

 

Основные элементарные функции:

1.                    Степенная у = хⁿ, где n- действительное число;

2.                    Показательная у = а^x, где а- положительное число;

3.                    Логарифмическая у =log_а x, где а>0;

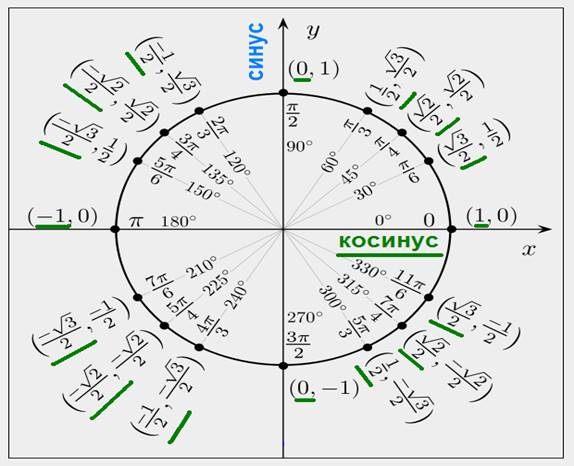
4.                    Тригонометрические: у = sin x; у = cos x;

5.                     у = tg x;

             у = ctg x.

6.                      Обратные тригонометрические: у = arcsin x; у = arccos x;

            у = arctg x; у = arcctg x

 

Тренинг умений.

 

Задача. Проволоку длиной 135 м разрезали на две части так, что одна из них короче другой в 2 раза. Найти длину каждой части.

Решение:   х+2х=135

3х=135

х=135/3

х=45

Ответ: I = 45 м         П= 90 м.

 

Задача. Купим 9 м проволоки двух видов (алюминиевую и медную) по цене 20 руб за метр и 30 руб за метр. За всю покупку заплатили 220 руб. Сколько метров проволоки купили каждого вида?

Решение:

 

20х+30у=220

х+ у=9

х=9-у

20(9-у) +30у=220

180-20у+30у=220

у=4 (медная)

х=9-4

х=5 (алюминиевая)

Ответ: у=4 (медная); х=5 (алюминиевая).

 

Задача. Бригада монтеров могла окончить электропроводку в 4 ч. Дня, прокладывая в час по 8 м. После выполнения половины всего задания один рабочий выбыл из бригады; в связи с этим бригада стала прокладывать в час по 6 м. и закончила запланированную на день работу в 6 ч. Вечера. Сколько метров провода было проложено и за сколько часов?

 

Решение:

Пусть первоначально планировалось проложить электропроводку за t часов. Прокладывая по 8 м. электропроводки в час, было бы проложено 8 t метров. Проложив половину электропроводки в 4 t метров за t /2 часов, из-за уменьшения состава бригады пришлось в дальнейшем работать на 2 часа дольше (работа была закончена в 6 ч. Вечера вместо планируемых 4 ч. вечера). Стало быть, бригада работала (t/2+ 2) часа, прокладывая по 6 метров электропроводки в час, и проложила оставшиеся 4 t метров электропроводки. Поэтому

4 t + 6(t/2 + 2), t=12 ч.

Следовательно, было проложено 8∙t=96 м. электропроводки за t+2=14 часов.

Ответ: 96 м, 14 ч.

Вопросы и задания для самопроверки.

2.1. Обратите внимание на встретившиеся в тексте следующие ключевые слова и обозначения: функция, область определения функции, график функции, у = f(x). Приведите примеры их использования.

2.2. Какие способы задания функции вы знаете?

2.3. Двое рабочих за смену вместе изготовили 72 детали. После того как первый рабочий повысил производительность труда на 0,15, а второй – на 0,25, вместе за смену они стали изготовлять 86 деталей. Сколько деталей изготовляет каждый рабочий за смену после повышения производительности труда?

 

 

 

2.2. УРАВНЕНИЯ

Равенство с переменной называется уравнением.

Решить уравнение- значит найти все его корни или доказать, что их нет.

Решение уравнений:

1. а) С помощью уравнений-следствий;

- преобразования, гарантирующие сохранение верного равенства.

в) Проверка корней;

-  подстановкой в исходное уравнение.

2. С помощью равносильных преобразований. Учесть ОДЗ исходного уравнения;

- сохранять на ОДЗ верное равенство при прямых и обратных преобразованиях.

3. Применением свойств функций;

- исходное уравнение;

- уравнение, полученное в результате преобразования исходного;

- символическое изображение направления выполненных преобразований.

Тренинг умений.

Задача. Имеется два куска кабеля разных сортов. Масса первого куска равна 65 кг; другой, длина которого на 3 м. больше длины первого и масса каждого метра которого на 2 кг больше массы каждого метра первого куска, имеет массу 120 кг. Вычислить длину этих кусков.

Решение:

Пусть х - длина первого куска кабеля в метрах, тогда масса одного метра этого кабеля равна   кг. Следовательно, масса одного метра второго кабеля равна

 ( +2) кг, а длина второго кабеля равна (х+3) м. Стало быть, масса второго кабеля, с одной стороны, равна

( +2)(х+3) кг, а , с другой стороны, равна 120 кг. Получаем уравнение (+2)(х+3)=120

х=5, х=19,5

      х=8, х=22,5

Задача. Двое электриков, работая вместе, выполняют некоторую работу за 8 ч. Первый из них, работая отдельно, может выполнить всю работу на 12 ч. скорее, чем второй, если тот будет работать отдельно. За сколько часов каждый из них, работая порознь, может выполнить работу?

Решение.

Пусть первый электрик может самостоятельно выполнить работу за х ч., тогда второй- за (х+12) ч. Скорость работы первого рабочего ( в долях от всей работы за час) 1/х (1/ч), а второго 1/х+1 (1/ч), а скорость при совместной работе равна  1/х + 1/х+12 (1/ч)

Так как рабочие вместе выполняют всю работу за 8 часов,

то (1/х + 1/х+12)·8=1

х = 12, х=24

Задача. Себестоимость единицы изделия и количество выработанной продукции находятся в обратно пропорциональной зависимости. При тех же производственных затратах количество выработанной продукции увеличилось на определенную часть. На какую часть уменьшится себестоимость изделия?

Решение:

Обозначим количество продукции через х, себестоимость единицы изделия через у, производственные затраты через V. Тогда у=v/x. Пусть количество продукции увеличилось на определенную часть, равную , тогда новое количество продукции станет равным x₁=x+  . При тех же затратах новая себестоимость

у₁ = v/x₁=  =

y-y₁=y- =           

Следовательно, если количество выработанной продукции увеличить на m/n часть, то при тех же производственных затратах себестоимость единицы изделия уменьшится на   ее часть.

Задача. Планом было предусмотрено, что предприятие на протяжении нескольких месяцев изготовит 6000 насосов. Увеличив производительность труда, предприятие стало изготовлять в месяц 70 насосов больше, чем было предусмотрено и на один месяц раньше установленного срока перевыполнило задания на 30 насосов. На протяжении скольких месяцев было предусмотрено выпустить 6000 насосов.

Решение. Пусть планом было предусмотрено выпускать Х насосов в месяц. На выпуск 6000 насосов ушло бы 6000/x месяцев. При выпуске х+70 насосов в месяц предприятие выпустило 6030 насосов за 6030/x+70 месяцев. Так как при этом был сэкономлен месяц, то 6000/x=6030/x+70+1,

Х=600. Выпуская по плану 600 насосов в месяц, предприятие потратило бы на выпуск 6000 насосов 10 месяцев.

Вопросы и задания для самопроверки.

2.4. Объясните на примерах, как можно использовать свойства функций при решении уравнений.

2.5. Бригада рабочих должна была изготовить за смену 7200 деталей, причем каждый рабочий делал одинаковое количество деталей, однако в бригаде заболело трое рабочих и поэтому из оставшихся рабочих пришлось сделать на 400 деталей больше. Сколько рабочих было в бригаде?

2.6. При включении в электрическую цепь дополнительного сопротивления R ом, сила тока уменьшается на J А. Напряжение в цепи равно U в. Найти первоначальное сопротивление. Напряжение U, сила тока J и сопротивление R электрической цепи связаны законом Ома:  U=J R

 

 

 

 

 

 

2.3. НЕРАВЕНСТВА

Если два выражения с переменной соединить одним из знаков>,<, то получим неравенство с переменной.

f (x)> g (x)

Решением неравенства с переменной называется значение переменной, которое обращает заданное неравенство в верное числовое неравенство.

Решение неравенств: 1. С помощью рациональных преобразований;

- учесть ОДЗ исходного неравенства;

-сохранять на ОДЗ верное неравенство при прямых и обратных преобразованиях.

2. С помощью метода интервалов f (x)>0, f (x)< 0;

-найти ОДЗ;

-найти нули функции: f (x)=0;

-отметить нули на ОДЗ и найти знак функции на каждом промежутке, на которые разбивается ОДЗ;

-записать ответ, учитывая знак заданного неравенства.

Тренинг умений.

Задача. На станции технического обслуживания установлено несколько электродвигателей общей мощностью N кВт. Расстояние от места ввода до магистрали равно l км, а удельное сопротивление проводов, соединяющих ввод с магистралью, - p. Определить допустимое сечение этих проводов, если напряжение в магистрали U в., а потери напряжения в линии не должны превышать U в.

 

Решение.

Пусть S-искомое сечение проводов, R₁- сопротивление подводящей линии, R₂- внутреннее сопротивление двигателей.

По формуле R=l ρ/s, то R₂=2l ρ /s. На основании закона Ома  I=U/(R₁ + R₂). По условию U R₁< U₁ ,так как напряжение двигателя равно U-U₁ то, учитывая, что N=(U-U₁ )²/R₂, будем иметь R₂= (U –U₁ )²/ N . Отсюда 2U ρ l/s(2 ρ l/s+(U-U₁)²/N)≤U₁, откуда S≥ 2 ρ lN/U₁(U-U₁).

 

Вопросы и задания для самопроверки:

2.7.             Объясните на примерах смысл понятий:

«решение неравенства»,

«решить неравенство», «область допустимых значений неравенства»,

«равносильные неравенства».

2.8.             Прямой коридор элеватора, длина которого равна А=20 м., освещается тремя электрическими лампочками, расположенными по прямой на высоте h=4 м. над полом. Две лампочки размещены по концам коридора и имеют одинаковую силу света, а третья находится точно в середине коридора. Формула освещенности

E=(J/R²) cos α Определить, какую силу света должна иметь каждая лампочка, чтобы в конечных точках коридора освещенность составляла не менее 8 лк., а в его средней точке - не более 10 лк.

 

 

 

 

 

 

 

2.4. СИСТЕМЫ УРАВНЕНИЙ

Решить систему уравнений - значит найти множество всех ее решений.

Решение системы линейных уравнений:

- способ сложения уравнений; -способ подстановки.

Тренинг умений.

Задача. Два электрика, работая одновременно на одном объекте 12 ч. За какое время каждый электрик по отдельности выполнит работу, если скорость выполнения работы относится, как 3:2?

Решение. Пусть х - время работы первого электрика, у – второго.

Скорость работы за час первого и второго электрика:     1/x +1/y.

За час два электрика вместе выполнят работу 1/x+1/y, следовательно, будут работать   часов. Как известно, это время равно 12 часам. Возникает система уравнений.

y/x=3/2                          y=3x/2

 = 12,            x y= 12(x+y), x= 0,

y=30   x=20

Задача. В магазин для продажи поступили лампочки 60V и 100V. Когда продали 50 % лампочек 60 V и 20 % лампочек 100 V, что составили в общей сложности 390 лампочек, то лампочек 60 V осталось в 3 раза больше, чем 100V. Сколько поступило в магазин лампочек 60V   и 100V.

Решение: Пусть в продажу поступило m лампочек 60V и n-лампочек 100V. Первая распроданная партия лампочек состояла из 390 штук. В партию входили 50 % всех лампочек 60V, то есть 0,5 m лампочек, и 20 % всех 100V, то есть 0,2 n лампочек.

Следовательно, 0,5m+0,2n= 390.

Отношение количества оставшихся лампочек 60V (0,5m) к количеству оставшихся лампочек 100V (0,8n) равно 3. Решим получившуюся систему уравнений   0,5m+0,2n=390

m=720, n=150

0,5m/0,8n= 3

Задачи для самопроверки:

2.9.  Бригада рабочих должна была изготовить 8000 одинаковых деталей в определенный срок. Фактически эта работа была окончена на 8 дней раньше срока, т.к. бригада делала ежедневно на 50 деталей больше, чем было намечено по плану. В какой срок должна была быть окончена работа и каков ежедневный процент перевыполнения плана?

2.10.         Двум электрикам была поручена работа. Второй приступил к работе на час позже первого. Через 3 часа после того, как первый приступил к работе, им осталось выполнить 9/20 всей работы. По окончании работы оказалось, что каждый выполнил половину всей работы. За сколько часов каждый, работая отдельно, может выполнить всю работу?

2.11.         Двум рабочим было поручено изготовить партию одинаковых деталей. После того, как первый проработал 2 ч., а второй 5 ч., оказалось, что они выполнили половину всей работы. Проработав совместно еще 3 ч., они установили, что им осталось выполнить 0,05 всей работы. За какой промежуток времени каждый из них, работая отдельно, может выполнить всю работу?

 

 

 

 

 

 

 

3.ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ.

Синус и косинус, а также тангенс и котангенс являются функциями величины угла, которые называются тригонометрическими функциями.

Основные параметры и формы представления переменного тока.

е = Вlvsinα = Esinwt  (1), где  В - магнитная индукция поля, Тл; V- скорость движения (м/с) проводников рамки длиной l, м; α- угол между плоскостью рамки  и силовыми линиями поля.

Задача. Квадратная рамка вращается вокруг оси, расположенной      посередине, с постоянной частотой n = 3000 об/ мин в равномерном магнитном поле, имеющем индукцию В= 1 Тл. Длина одной стороны рамки l = 0,4 м, а число витков w= 10. Записать выражение для мгновенного значения э д с, определить период и частоту.

Решение. Мгновенное значение э д с соответствует выражению (1). Амплитудное значение, учитывая, что э д с наводится в двух проводниках рамки, равно Е_m = 2ωBlυ, где угловая частота ω= 2πn/60 = 314 рад/с. Для нахождения линейной скорости рамки определяем радиус вращения, который в данном случае равен l/2, т.е. υ= ωl/2= 62,8 м/с.

Амплитудное значение э д с Е_m= 2.10.1.0,4.62,8= 502 В, мгновенное значение е= 502sin 314t. Период и частоту можно найти по формулам f= ω/2π= 50 Гц  и Т= 1/f= 0,02 c= 20 мс.

Задача. К трем источникам с одинаковым напряжением, мгновенное значение которого определяется по выражению u= 59sin(314t-45⁰) В, подключены резистор, катушка индуктивности и конденсатор. Найти выражения для мгновенных значений токов в каждом случае и определить их действующие значения, если R= 10 Oм; L= 10 мГн  и С= 1 мкФ.

Решение. В цепи с резистором мгновенное значение тока совпадает по фазе с напряжением и по закону Ома i_R= u/R= 5?9sin(314t-45⁰) A. Действующее значение соответственно равно I= U_m/R= 4,2 A.

В цепи с катушкой индуктивности ток отстает по фазе от напряжения на 90^o, ее реактивное сопротивление Х_L= ω L= 3,14 Ом, а мгновенное значение тока

 i_L= 18,8sin(314t-45⁰) А, действующее значение

I= U_m X_L= 13,3 A.

В цепи с конденсатором ток опережает по фазе напряжение на 90⁰, его реактивное сопротивление

Х_c= 1/ ω C= 3,18 кОм, мгновенное значение тока

i= 18,5sin(314t+45^o) A, а действующее значение

I= U_m  X_c= 13,1 A.

Задачи для самопроверки.

3.1. Проводник длиной 0,5 м равномерно вращается с линейной скоростью v= 50 м/с в магнитном поле с индукцией В= 1,5 Тл . Определить э д с, наводимую в проводнике, если радиус вращения составляет 0,2 м, а ось вращения параллельна проводнику.

3.2. Действующие значения напряжения и тока потребителя электрической энергии в комплексной форме изображаются в виде U= 150+j160, B и

I= 4-j3,A. Записать выражения для мгновенных значений тока и напряжений при частоте f= 50 Гц, определить в комплекс ной форме полное сопротивление.

 

 

 

4. ПРОИЗВОДНАЯ

Протекание тока в электрической цепи

 (задача о мгновенной величине тока).

Представим себе электрическую цепь с некоторым источником тока. Обозначим через q= q(t) количество электричества ( в кулонах), протекающее через поперечное сечение проводника за время t. Тогда q(t)-q(t) есть количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t . Средней силой тока за указанный промежуток времени называется число

I_ср=           

В случае постоянного тока средняя сила тока I будет одинаковой для любых различных, но одинаковых по длительности промежутков времени. Если в цепи переменный ток, то I, будет различной для различных, но одинаковых по длительности промежутков времени. Поэтому для характеристики цепи переменного тока вводят понятие мгновенной силы тока, или силы тока в данный момент времени: мгновенной силой тока I(t) в момент времени t называется предел (если он существует), к которому стремится средняя сила за промежуток времени от t до t,

I=  

Производной функцией в точке х называется предел функции к приращению аргумента при стремлении х к нулю: у^'=f^' (x)=lim  

Тренинг умений.                                                                              _Δx→0

Задача. Количество электричества, протекающее через проводник, начиная с момента t=0, выражено формулой Q= 5t²+2t (кулонов). Вывести формулу для вычисления силы тока в любой момент времени и определить силу тока в конце третьей секунды.

Решение.  I= = 10t + 2, I(3) = 10.3 = 30 (A).

Задача. Пусть электрическая лампочка движется с помощью блока вдоль вертикальной прямой ОВ. На каком расстоянии от горизонтальной плоскости следует ее разместить, чтобы в точке А этой плоскости освещенность была наибольшей ( ОА = а).

Решение. Освещенность Е= к sinx/r, где к- коэффициент пропорциональности, х = ОВ, sinx= x/r, cледовательно,

E = k·sinφ/r², sinφ=x/r, r=,  0‹х‹∞. Следовательно,

Е=кх/( х²+а²)^3/2;  Е¹(х)= ( ка²-2х²)/(х²+а²)^5/2;

 к( а²-2х²)/(х²+а²)^5/2=0

x=а/

Задача. Изменение силы тока в зависимости от времени выражено уравнение I= 2t²-5t. ( I- в амперах, t- в секундах). Найти скорость изменения силы тока в конце 10-й с.

Решение: V = 4t-5, V(10) = 4.10-5 = 35 A/c

Задача. Найти силу тока I, если количество изменяется по закону Q(t)=2t² + 1 электричества, проходящее через поперечное сечение проводника за 10 с.

Решение: I = 4t ,         I(10) = 4.10 = 40 ( A ).

Задача. Над центром круглого стола радиуса висит лампа. На какой высоте следует подвесить эту лампу, чтобы на краях стола получить наибольшую освещенность.

Решение: Е = к sin α/ (h² + r²⁾ ,         

                   sin α  = h/ ,

Вместо функции E = kh/(h² + r²)^3/2 рассмотрим функцию  T = E²/ k² = h² /( h² + r²)³, вместо h² = z.

T^' =( z/( z + r²)³) ^'  =( z + r² – 3z)/( z + r² )⁴,    T^' = 0,   

 r² – 2z = 0 ,    z = r² /2 ,

h² = r²/ 2.

Освещенность максимальна, если h = r/, т.е.,

если tg φ = h/r = 1 /

 

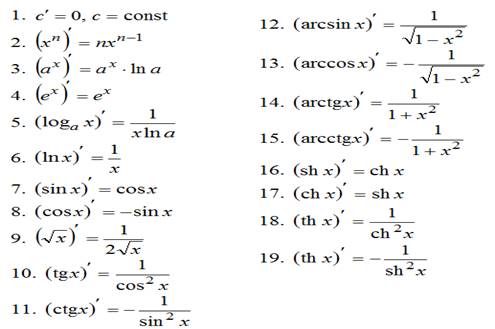
Вопросы и задачи для самопроверки.

4.1     . При равномерном протекании заряда по проводнику силой тока

называется заряд, протекающий за единицу времени. Дайте определение

силы тока в общем случае.

4.2.  Количество электричества, протекающее через проводник, начиная с момента t= 0, задается формулой q = 3t² + t + 2. Найдите силу тока в момент времени t= 3.

4.3. В какие моменты времени ток в цепи равен нулю, если количество электричества, протекающего через проводник, задается формулой:

а) q = t + k/t ,          b) q = 4t + 2

4.4.  Измерения величины заряда на обкладках конденсатора показали, что заряд меняется со временем по закону q(t)= 3,05 + 6,11 t² – 0,8t+1. Найдите закон изменения силы тока.

4.5. Установлено, что энергия, отдаваемая электрическим элементом, определяется по формуле

W = E R / ( r + R ), где E- электродвижущая сила элемента; r- внутреннее сопротивление; R- внешнее сопротивление. Каким должно быть сопротивление цепи, чтобы отдаваемая элементом энергия W была наибольшей?

4.6. Определить сопротивление внешней цепи, при котором батарея из двух последовательно соединенных аккумуляторов сможет развить максимальную полезную мощность. ЭДС батареи 2,5 В, внутреннее сопротивление 0,16 Ом. Чему равна максимальная полезная мощность?

5.                    ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Если функция f(x) в точке х имеет производную, то произведение f(x) . X называется дифференциалом функции f в точке х и обозначается df(x).

Дифференциальные уравнения- это уравнения, связывающие неизвестную функцию и ее производные.

Электрическая цепь.

Рассмотрим электрическую цепь, состоящую из последовательно соединенных сопротивления и конденсатора. Будем считать, что в цепи сделано короткое замыкание и конденсатор, имевший начальный заряд, начинает разряжаться. Напряжение на конденсаторе в момент времени t обозначим через U(t). Заряд q(t) связан с напряжением U формулой q= CU, где С- емкость конденсатора. Через сопротивление пойдет ток, который связан с напряжением U формулой U= - RI, где R-величина сопротивления (закон Ома), а знак «-» связан с направлением тока. Появление тока связано с изменением заряда q, и, значит, величина I является скоростью изменения заряда во времени: I= dq/dt. Подставляя в эту формулу вместо I выражение –U/R, а вместо q выражение CU, получим уравнение для напряжения: CdU/dt= -U/R,        dU/dt= -IU/RC

Решение дифференциального уравнения- это функция, при подстановке которой уравнение превращается в тождество.

Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора (с емкостью С) и катушки ( с индуктивностью L). Будем считать, что на конденсаторе есть начальное напряжение, в цепи сделано короткое замыкание и пошел ток через катушку. Обозначим через U= U(t) напряжение на конденсаторе в момент времени t. Напряжение на катушке пропорционально скорости изменения тока I, проходящего через катушку, т.е. U= -LdI/dt. Выражая обычным образом, ток I через заряд I= dq/dt и заменяя заряд q через CU, получим: U= -LdI/dt= - LC d U/ dt = - U/LC

Тренинг умений.

Задача. Изолированному проводнику сообщен заряд Q единиц. Вследствие несовершенства изоляции проводник постепенно теряет свой заряд. Скорость потери заряда в данный момент пропорциональна наличному заряду проводника. Какой заряд останется на проводнике по истечении t мин?

Решение: Пусть к моменту t заряд проводника равен Q. Скорость потери заряда в этот момент равна- dQ/dt. Так как эта скорость пропорциональна заряду Q, то получим следующее дифференциальное уравнение:

- (dQ/dt)= kQ,  k- коэффициент пропорциональности. Интегрируя это уравнение, получим общее решение:

Q= C e^-kt . Используем начальное условие: при t=0, Q=Q₀; тогда Q= C l^-k*0   u C=Q₀. Следовательно, закон протекающего процесса записывается так: Q= Q₀ e^-kt

Задачи для самопроверки.

5.1 Электрическая цепь состоит из последовательно включенного источника постоянного тока, дающего напряжение V, сопротивления R, самоиндукции L и выключателя, который включается при t=0. Найдите зависимость силы тока от времени.

5.2 Электрическая цепь состоит из последовательно включенного источника т ока, напряжение которого меняется по закону

E=V sinwt, сопротивления R и самоиндукции L. Найдите силу тока в

цепи при установившемся режиме.

 

 

 

 

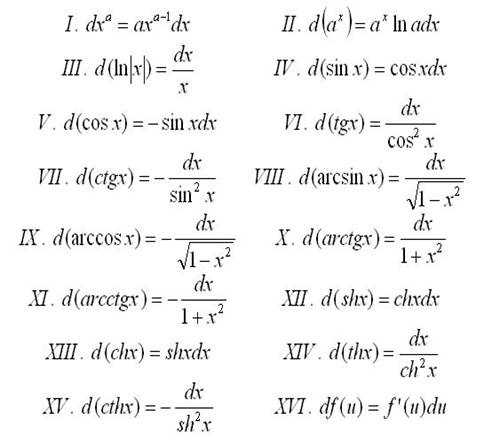
6.    ИНТЕГРАЛ.

Дифференцируемая функция F(x), x принадлежит отрезку (а; б ), называется первообразной функцией для функции f(x) на интервале (а; б), если F(x)= f(x) для каждого х принадлежит отрезку (а; б ).

Совокупность всех первообразных, т.е. выражение вида F(x) + C, где F(x)- первообразная функции f(x) называется неопределенным интегралом функции f(x):    f(x)dx= F(x) + C

Определенным интегралом называется число, равное площади криволинейной трапеции, ограниченной непрерывной кривой y= f(x) (f(x)>0 на отрезке [a,b], осью ОХ, и прямыми х = а, х = б.

Тренинг умений.

Задача. Найти количество электричества, проходящее через поперечное сечение проводника за 10 с, если сила тока изменяется по закону I(t)= (4t+ 1)

Решение.Q= (4t+1) dt= (2t² +1) │¹⁰ =210 Kл.

Задача. Экспериментально установлено, что продуктивность труда работника приближенно выражается формулой: f(t)= -0,0033t² – 0,089t+ 20,96, где t- рабочее время в часах. Вычислить объем выпуска продукции за квартал, считая рабочий день 8-часовым, а количество рабочих дней в квартале- 62.

Решение: Объем выпуска продукции  V=f(t)dt. В течение квартала объем выпуска продукции составит:

V= 62 f(t)dt= 62(0,0033t²-0,089t+20,96)dt=

62(-0,001.512-2,848+167,68) =10185(ед).

Задача. Предположим, что в точку О помещен единичный электрический заряд. Он создает электрическое поле. Найти работу электрического поля по перемещению единичного заряда из точки х в точку х.

Решение: Мы знаем, что на другой единичный заряд, помещенный в точку х, действует сила, обратно пропорциональная квадрату расстояния, т.е. F(x)=k/x². Применяем формулу для работы, получим:

А= k dx/x² = k dx/x²,для функции F(x)=k'/x² первообразную U(x) можно найти по таблице: U(x)=-k/x. Получим: A=U(x) =-k/x=k/x₁-k/x₂

Функция U(x)= -k/x называется потенциалом электрического поля.

Задачи для самопроверки.

6.1. Найти количество электричества, проходящее через поперечное сечение проводника за 20 с., если сила тока изменяется по закону I(t)= 2t+ 1

6.2. Продуктивность труда бригады рабочих на протяжении смены приближенно определяется формулой f(t)=-2,53 t² +24,75t+111,1, где t- рабочее время в часах. Определить объем продукции, изготовленной бригадой за 5 рабочих часов.

6.3. Производительность труда рабочего в течение смены приблизительно выражается функцией

y= 0,1t-t+17, t-часы работы. Определить среднюю производительность рабочего.

 

 

 

7.   ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

 

Теория вероятностей - математическая наука, которая изучает закономерности в случайных событиях.

К основным понятиям теории вероятностей относятся испытания и события.

Под испытанием понимают реализацию данного комплекса условий, в результате которого непременно произойдет какое-либо событие.

Например: бросание монеты- испытание; появление цифры- события.

Случайным событием называется событие, связанное с данным испытанием, которое при осуществлении испытания может произойти. А может и не произойти.

Например: выстрел по цели- это испытание, случайные события в этом испытании - попадания в цель или промах.

Математической вероятностью события А называют отношение числа m случаев, благоприятствующих появлению события А, к числу n всех равновозможных единственно возможных и несовместных случаев.

Р(А)= m/n

Эта формула носит название классического определения вероятности.

Задача. Телефонная линия, соединяющая два пункта А и В, расположенных один от другого на расстоянии 2 км, оборвалась в неизвестном месте. Какова вероятность того, что обрыв находится не дальше 450 м. от пункта А?

Решение: Р(А)= m/n= 450/2000= 0,225

Задача. На 8 карточках напечатана одна из следующих букв  е, г, т, ф, е, р, л, а. Вынимая последовательно из ящика наугад и выкладывая их в одну линию, можно получить слово телеграф. Какова вероятность этого события.

Решение: m=1, n=Р равно числу перестановок из 8 букв.

Р ₈=8! =1∙2∙3∙4∙5∙6∙7∙8= 40320         Р=m/n= 1/40320

Задача. В коробке находятся электролампы 5 шт. по 75 Вт и 6 шт. по 100 Вт . Из коробки вынимают одновременно две электролампы. Какова вероятность того, что обе лампочки 100 вт.

Решение. Здесь число равновозможных независимых исходов составляет

n== =55

Событию А благоприятствуют

=  =  =15 исходов. Следовательно, P(A)=15/55=3/11.

Задача. Набирая номер телефона, абонент забыл две последние цифры и , помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно?

Решение: Две последние цифры можно набрать   способами, а благоприятствовать событию А ( цифры набраны правильно) будет только один способ. Поэтому P(A)=1/=   =1/90

Задача. Среди 100 электроламп 5 бракованных. Какова вероятность того, что выбранные наудачу з электролампы окажутся не бракованными?

Решение: Из 100 электроламп 3 лампы можно выбрать   способами. Три не бракованных электроламп из общего числа 95 рабочих электроламп можно выбрать.     способами, следовательно, искомая вероятность равна

Р=/=(95·94·93)/(100·99·98)=0.86

 

Вопросы и задачи для самопроверки.

7.1.В цеху работают 6 мужчин и 4 женщины. В смену отобрали подряд 7 человек из 10. Какова вероятность того, сколько женщин и мужчин попадут в смену?

7.2. На каждой из восьми карточек напечатаны буквы с, ь, в, з, а, в, у, я. Карточки перевернуты и перемешаны. Какова вероятность, что, взяв 5 из них, можно получить слово «связь»?

7.3. В партии из 20 изделий четыре бракованных. Найти вероятность того, что среди пяти взятых наугад изделий окажется два бракованных.  (событие В).

7.4. Набирая номер телефона, абонент забыл последнюю цифру и набрал ее наугад. Найти вероятность того, что номер набран правильно. Решить задачу для случаев, если последняя цифра номера: а) четная; б) не более 6.

 

 

ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ     ВЕРОЯТНОСТЕЙ. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.

В рассмотренных выше задачах вероятность событий вычислялась непосредственно исходя из определения. К сожалению, этот путь приводит к успеху только в самых простых случаях. Обычно же прямой подсчет, как всех исходов, так и тех из них, которые являются благоприятствующими, оказывается неудобным, а иногда и практически невозможным из-за своей чрезмерной сложности. Вычисление вероятностей событий, как правило, можно существенно упростить, если использовать теоремы, устанавливающие связи между вероятностями событий.

Вероятность наступления какого- либо одного из нескольких несовместных событий равна сумме их вероятностей Р= Р(А₁) +…+Р(А_n).

Вероятность совместного наступления двух зависимых событий равна произведению вероятностей

 Р (А и В) = Р(А)·Р_A(В), Р_A(В)-условная вероятность события В, при условии, что событие А уже наступило. Если события независимы, то Р (А и В) = Р(А)·Р(В).

Пусть события А₁, А₂…А_n образуют полную группу. Если событие В может наступить совместно с одним из событий А образующих группу, то вероятность события А определяется по формуле P(B)=P(A₁)·P_A1(B)+P(A₂)·P_A2(B)+…+P(A_n)·P_An(B)

Формула носит название формулы полной вероятности.

Тренинг умений.

Задача. На склад поступили электроутюги, 80 % с первого завода и 20 % со второго. Среди продукции первого завода 90 % выдерживают гарантийный срок, со второго завода- 95 %. Какова вероятность, что взятый наугад со склада утюг выдерживает гарантийный срок? Какова вероятность, что утюг с первого завода?

Решение:

Р (A₁) =0,8- вероятность, что утюг поступил на склад с первого завода.

Р (A₂) =0,2- со второго.

Условные вероятности Р _A1(B) =0,9 и Р_A2(B) =0,95- что утюг выдержит гарантийный срок с первого завода и со второго.

1) Полная вероятность, что он прослужит определенное время, независимо с какого он завода, равна P(B)=P(A₁)·P_A1(B)+P(A₂)·P_A2(B)=0,8·0,9+0,2·0,95=0,91      2)Вероятность, что утюг с первого завода равна

P_B(A₁) = P(A₁)· P_A1(B)/P(B)=0,8·0,9/0,91=0,79

Задача. Автомат штампует детали. Вероятность того, что за одну смену не будет изготовлено ни одной нестандартной детали, равна 0,9. Какова вероятность того, что будут стандартными все детали, изготовляемые за три смены?

Решение: Р(А)= 0,9 По теореме о вероятности независимых событий,

Р(В)= Р(А)·Р(А)·Р(А)= 0,9·0,9·0,9= 0,729

Задача. Радиостанция 1, 2,3 независимо одна от другой посылают по одной передаче радиостанции 4. Вероятности приема передачи радиостанцией 4 от станции 1, 2, 3 соответственно равны Р₁=0,4, Р₂=0,5, Р₃=0,7. Найти вероятность того, что станцией 4 будет принята: а) только одна передача; б) хотя бы одна передача.

Решение.: а) Вероятность того, что станцией и будет принята только одна передача: P(A)=P (A₁A₂ A₃) + P (A₁A₂ A₃) +P (A₁A₂ A₃)=0,4·0,5·0,3+0,6·0,5·0,3+

+0,6·0,5·0,7=0,06+0,09+0,21=0,36

б) Прием передачи радиостанцией 4 от станции 1, 2, 3- взаимно независимые события. По теореме о вероятности осуществления хотя бы одного независимого события, вероятность того, что станцией 4 будет принята хотя бы одна передача:

P(A)=(1-P(A₁))· (1-P(A₂))·(1-P(A₃))=

1-(1-0,4)· (1-0,5)·(1-0,7)=1-0,6·0,5·0,3=

=1-0,09=0,91

 

 

 

ПОВТОРНЫЕ ИСПЫТАНИЯ.

Если производится n независимых испытаний, при каждом которых вероятность осуществления события А постоянна и равна Р, а затем противоположного события А равна q= 1- p, то вероятность P_n(m) того, что при этом событие А осуществляется ровно m, вычисляется по формуле Бернулли

P_n(m)=p^mq^n-m

Задача. Вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Чему равна вероятность того, что из 5 изготовленных на нем дeталей 3 будут нестандартными?

Решение: Воспользуемся формулой Бернулли для n=5, m=3, p=0,9, q= 0,1.

P_3,5=·0,9^3·0,1²=(4·5·0,729·0,01)/2=0,0729

 

Задачи для самопроверки.

 

7.5.  При проверке готовой продукции различают брак по форме и размерам. Вероятность брака по форме равна 0,05, по размерам- 0,01. Какова вероятность того, что взятая наугад деталь будет бракованной и по форме и по размерам?

7.6.  В магазин поступает 30 % электроламп с одного завода и 70 %- с другого завода. Среди ламп, с первого завода 85 % стандартных, а со второго завода- 75 % стандартных. Какова вероятность того, что купленная электролампа будет стандартной?

7.7.  Из 50 деталей 18 изготовлены в первом цехе, 20-во втором, остальные- в третьем. Первый и третий цеха дают продукцию отличного качества с вероятностью 0,9, второй цех- с вероятностью 0,6. Какова вероятность того, что взятая наудачу деталь будет отличного качества?

7.8.  Рабочий обслуживает 4 станка. Каждый станок за 6 часов работы несколько раз останавливается, и общая продолжительность остановок составляет 0,5 ч., причем остановки станков в любой момент времени одинаково вероятны. Найти вероятность, что в данный момент времени работает один станок.

7.9.  Рабочий обслуживает 50 станков. Вероятность того, что в течение смены станов потребует регулировки, равна 1/3. Что более вероятно:

а) регулировки потребуют 17 станков;

б) регулировки потребует 16 станков?

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайной называют величину, которая в результате испытания может принять одно и только одно возможное значение, наперед неизвестное.

Законом распределения случайной величины Х называют соответствие между ее значением х и вероятностью р появления этого значения.

Если х принимает отдельные числовые значения принадлежащие числовой оси, то случайная величина Х называется дискретной.

Если х принимает всевозможные значения, принадлежащие интервалу (а, в) числовой оси, то она называется непрерывной.

Математическое ожидание: М(Х)= n· р

Дисперсия: Д(Х)= n· p· q

Среднее квадратичное отклонение: σ=

Тренинг умений.

Задача. Найти математическое ожидание, дисперсию числа бракованных изделий в партии из 10000 изделий, если каждое изделие может оказаться бракованным с вероятностью 0,005.

Решение. Число бракованных изделий- это случайная величина Х, распределенная по биномиальному закону. Поэтому по формуле М(Х)= n ·р = 10000· 0,005= 50; 

Д(Х)= n∙p∙q= 10000·0,005·0,995= 49,75;

 

Задачи для самопроверки.

 

7.10.         Найдите математическое ожидание и дисперсию числа бракованных изделий в партии из 5000 изделий, если каждое изделие может оказаться бракованным с вероятностью 0,02.

7.11.         Из всей выпускаемой заводом продукции 98 % составляют изделия со знаком качества. Найдите математическое ожидание и дисперсию числа изделий со знаком качества в партии из 5000 изделий.

7.12.         Имеются 4 лампы, каждая из которых с вероятностью 1/3 имеет дефект. При ввинчивании в патрон дефектная лампа сразу перегорает, и тогда ввинчивается следующая. Рассмотрите случайную величину Х- число ввинченных ламп. Найдите закон распределения, математическое ожидание и дисперсию случайной величины Х.

 

ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЯМ.

1.1.          Пусть а- первоначальная цена товара, тогда а- 0,2а= 0,8 а- цена товара после первого снижения цен, 0,8а- 0,15.0,8а= 0,68 а- после второго снижения и 0,68а- 0,1.0,68а= 0,612а- после третьего снижения.

В результате цена была снижена на а-0,612а= 0,388а единиц стоимости, что составляет 0,388а/a. 100%= 38,8 %

1.2. Будем измерять производительность труда заработной платой p за час работы. Заработная плата за 8-часовый рабочий день равно 8p. Пусть х- прирост производительности труда в долях от первоначальной. Тогда р + рх- новая заработная плата за час работы, и

7( р + рх)- новая заработная плата за 7-часовый рабочий день. Прирост заработной платы равен 7(р + рх)- 8р= (7х-1)р, что составляет 5 % (0,05 доли) первоначальной заработной платы 8 р. Поэтому

(7х- 1)р/8p= 0,05,       x= 0,2,   x= 20 %.

1.3. Пусть х- количество продукции, выпускаемый по плану за месяц. Тогда в январе было выпущено 1,05х продукции, а в феврале 1,05х + 0,04.1,05х. Всего за 2 месяца при плане 2х выпущено 2,142х продукции, что составляет 2,142х/2x.100%= 107,1 %

1.4.( 1 способ) Прежде всего узнаем, на сколько сократились затраты провода в метрах.

225-198= 27 (м).

Затем определим, сколько процентов составляют 27 м. от 225 м.

27/225= 0,12= 12%

Следовательно, расход провода после внедрения новой схемы монтажа сократился на 12 %.

(2 способ) Сначала определим, сколько процентов от 225 м. составляет 198 м.

198/225= 0,88= 88 %

Теперь можно узнать, на сколько процентов уменьшились затраты т.к. 225 м. составляют 100 %, а 198 м.- 88 %, то находим 100 %- 88 %= 12 %

2.3. Пусть первоначальная производительность труда первого рабочего была х деталей за смену, тогда второго рабочего- 72-х деталей за смену. После повышения производительности труда первый начал производить 1,15х деталей за смену, а второй 1,25 ( 72-х) деталей за смену. Так как при этом они произвели 86 деталей, то 1,15х+1,25(72-х)= 86, откуда находим х=40. Следовательно, после повышения производительности труда, первый рабочий начал производить 1,15х= 1,15.40= 46 деталей за смену, а второй рабочий 1,25( 72-х)= 1,25.32= 40 деталей за смену. То есть 46, 40.

2.5. Пусть в бригаде было n рабочих, тогда норма изготовленных деталей каждому рабочему за смену равна 7200/n деталей. При увеличенной норме до 7200/n + 400 деталей за смену на рабочего, с изготовлением 7200 деталей справились n- рабочих (3 рабочих болели), поэтому

(7200/n + 400)(n- 3)= 7200,     n=9

2.6.( I R + 4 I R V) + IR)/2I

2.9. Пусть срок выполнения работы должен был быть равным t дням при изготовлении n деталей в день. Следовательно, t.n= 8000.

При ежедневном перевыполнении плана бригада изготавливала по n+50 деталей в день и изготовила все детали за t-8  дней, стало быть

(t-8)(n+50)= 8000

Мы получаем систему уравнений, которую легко преобразовать к виду:

t n= 8000

t n-8n + 50t-400= 8000,       t= 40, n= 200

2.10. Пусть первый рабочий может выполнить работу за х часов, а второй- за у часов. Тогда скорость работы первого рабочего 1/x, а второго 1/y.

Через 3 часа после того, как первый рабочий приступил к работе, он выполнил 3/x работы, а второй 2/x работы, т.к. он приступил к работе на час позже. Вместе они выполнили 11/20 работы, поэтому 3/x + 2/y= 11/20.

Пусть до конца работы первый рабочий проработал t часов, тогда второй t- 1 час. И первый и второй рабочий, как оказалось, выполнил половину всей работы. Поэтому t/x= ½    u  (t- 1)/y= 1/2

t = x/2        (x/2- 1)/y= ½

x-2= y

x-2= y

3/x + 2/y = 11/20,          x= 10,   y = 8

2.11. Пусть первый рабочий выполняет работу за х ч., второй за у часов. Тогда скорость работы за час для первого рабочего равна 1/x, а для второго 1/y.

За 2 часа первый рабочий выполнил 2/x работы, а второй за 5 часов выполнил 5/y работы, то  2/x+5/y= 1/2.

Проработав совместно еще 3 часа, они выполнили еще 3 (1/x+1/y) работы, что, как оказалось, на 0,05 меньше оставшейся половины работы. Поэтому 3/x+3/y= 9/20.

2/x+5/y= 1/2               1/x=u, 1/y=v,

1/x+1/y=3/20,              2u+5v= 1/2

u+v= 3/20,           u=1/12,  v=1/15,      x=12,   y=15.

То есть первый рабочий может самостоятельно за 12 ч., а второй за 15 ч.

3.1. Эдс проводника e= 37,5 sin 250 t.

3.2. Для нахождения мгновенных значений токов и напряжений запишем их в показательной форме U=·е^{j arctg 160/150}=220 e^j47 B и

J= е^{j arctg (-3/4}=5e^-j37A.

Амплитудные значения напряжения и тока U_m=U=311B и J_m=7,1A

Так как начальные фазы ψ_u=47^o  и ψ_i=-37^o , то окончательно получаем

i =7,1 sin (314t-37^o)A и U=311 sin (314t+47^o)B

Комплекс полного сопротивления равен отношению напряжения и тока:

Z=220e^j47/5e^j37=44^j84Oм

4.2. I(t)= 6t+1,  I(3)= 6·3+1= 19 (A).

4.3. а) t= ,    b) t= 0

4.4. I= 12,22t- 0,8 (A).

4.5. Энергия, отдаваемая электрическим элементом, будет наибольшей, когда R=r.

4.6. W=   (E²R)/(R+r)²         

R=r=0,16 , W_max =9,8 Вт.

5.1. Указание. Задача сводится к интегрированию уравнения L dI/dt + RI= V при начальном условии  I(0)=0.  I=V·(1-e^-Rt/L)/R

5.2. Указание. Задача сводится к отысканию периодического решения уравнения

LdI/dt+ RI= V sin wt.  I=V·sin(ωt-arctg ωl/R)/

6.1. Q=(2t+1)dt=t²+t=400+20=420КЛ

6.2. V=f(t)dt, V=(-2,53t²+24,75t+111,1)dt=

=-2,53t³/3+24,75t²/2+111,1t=

=-105,42+206,25+555,5=656,33(ед)

6.3. Используем теорему о среднем значении интеграла, определим среднюю производительность рабочего μ=Ydt/(b-a)=[ (0,1t²-t+17)dt]/8-0+[(0,1t³/3)-(t²/2)+17t)/8=15,2единицы продукции в 1 час

7.1. =10!/7!3!=(7!·8·9·10)/(7!·1·2·3)=120

Среди отобранных три женщины из четырех и четыре мужчины из шести. Таким образом, m==4!/3!1!·6!/4!2!=60

Р=m/n= 60/ 120= 0,5

7.2. m=1, n=        равно числу размещений из 8 по 5.

  =8!/(8-5)!=(3!·4·5·6·7·8)/3!=6720, p=m/n=1/6720

7.3. Здесь число равновозможных независимых исходов есть n==(20·19·18·17·16)/(1·2·3·4·5)=15504

Подсчитаем число исходов m,  благоприятствующих событию В. Два бракованных изделия из четырех можно выбрать =(4·3)/(1·2)=6 способами, а три стандартных изделия из 16 можно выбрать   =(16·15·14)/(1·2·3) =560                            способами. Каждая комбинация бракованных изделий может сочетаться с каждой комбинацией стандартных изделий, поэтому m= 560·6= 3360.

Следовательно, Р(В)= 3360/15504= 0,2

7.4. Цифры на телефонном аппарате образуют множество А={0,1,2,3,4,5,6,7,8,9}, n=10. Значит, вероятность того, что номер набран правильно Р(А)= 1/10.

а) Четные цифры на телефонном аппарате образуют множество В= {0,2,4,6,8}, n=5. Значит, Р(В)= 1/5.

7.5. Событие А- взятая наугад деталь будет бракованной и по форме и по размерам А= A₁·A₂ . По теореме о вероятности произведения независимых событий, Р(А)=P(A₁)·P(A₂) =0,05·0,01= 0,0005

7.6. А- купленная лампа будет стандартной;

А₁ -лампа, поступившая с первого завода будет стандартной.

Вероятность P(A₁)=0,85, P(A₁)=0,15,

А₂ –лампа, поступившая со второго завода, будет стандартной.

Вероятность P(A₂)=0,75, P(A₂)=0,25

В магазин поступает 30 %= 0,3 ламп с первого завода и 70 %= 0,7- со второго завода, тогда, P(A)=0,3·0,15+0,7·0,25=0,22

P (A)=1-P(A)=1-0,22=0,78

7.7.P(H₁)=18/50, P(H₂)=20/50, P(H₃)=12/50

P(A/H₁)=0,9, P(A/H₂)=0,6, P(A/H₃)=0,9

По формуле полной вероятности находим искомую вероятность P(A)=P(H₁)·P(A/H₁)+P(H₂)·P(A/H₂)+P(H₃)·P(A/H₃)=

=(9·18)/(10·50)+(6·20)/(10·50)+

+(9·12)/(10·50)=39/50=0,78

7.8. Вероятность остановки одного станка 0,5 / 6=1/12, а вероятность того, что станок работает, 1- 1/12=11/12. Воспользуемся формулой Бернулли

P_m,n=p^mq^n-m     A₁-работает один станок

P(A₁)= ·11/12·(1/12)³=(4·11)/12⁴=11/5184=0,0021

7.9. Вероятность одна и та же.

(·(1/3)¹⁷·(2/3)³³=·(1/3)¹⁶·(2/3)³⁴)

7.10.         М(Х)== 100, Д(Х)= 8

7.11.         М(Х)= 4900, Д(Х)= 98

7.12.          

 

1	2	3	4
2/3	2/9	2/27	1/27

 

    М(Х)=40/27, D(X)=452/729

 

О Г Л А В Л Е Н И Е

 

Предисловие…………………………………………2

Введение……………………………………………. 5

1.                    Повторение. Проценты………………………6

2.                    Функции, уравнения, неравенства и системы 

           уравнений    

2.1                Функции………………………………………8

2.2                Уравнения……………………………………10

2.3                Неравенства………………………………… 12

2.4                Системы уравнений…………………………13

3.                    Тригонометрические функции……………. 14

4.                    Производная…………………………………15

5.                    Дифференциальная функция……………… 17

6.                    Интеграл……………………………………. 19

7.                    Элементы теории вероятностей……………21

           Ответы и указания к решениям    ………… 26