Счетчики

Практическая работа №7

Тема: Счетчики

Цель: Исследование работ следующих схем:

           счетчики: асинхронный и синхронный;

           счетчики прямого счета и реверсивный;

           делитель частоты;

Вид работы: индивидуальный

Время выполнения: 2 часа.

Теоретические сведения

Счетчиками называют последовательные цифровые устройства, предназначенные для подсчета и запоминания числа импульсов, поданных в определенном временном интервале на его счетный вход. Помимо счетного счетчики могут еще иметь входы асинхронный или синхронной установки начальных состояний. По характеру изменения состояний счетчика счетными импульсами различают суммирующие, вычитающие и реверсивные счетчики. По способу организации переносов между разрядами их можно разделить на счетчики с последовательным, сквозным, параллельным и комбинированным переносом. Счетчики с последовательным и сквозным переносом называют асинхронными, а с параллельным переносом – синхронными. Обычно счетчик содержит одни или несколько идентичных разрядов, построенных на основе двоичных триггеров. Количество различимых состояний разряда счетчика является его классификационным признаком, согласно которому счетчики называют двоичными, двоично-десятичными и т. д.

Счетчики и делители подразделяются на асинхронные и синхронные. У синхронных счетчиков все разрядные триггеры синхронизируются параллельно одними и теми же синхроимпульсами, поступающими из источника этих импульсов. Асинхронные счетчики имеют последовательную синхронизацию, т.е. каждый последующий разрядный триггер синхронизируется выходными импульсами триггера предыдущего разряда. Асинхронные счетчики иногда называют последовательными, а синхронные счетчики - параллельными.

Синхронные счетчики, в свою очередь, подразделяются на параллельно-синхронные и последовательно-синхронные. Параллельные счетчики имеют более высокую скорость счета, чем асинхронные.

Счетчики, независимо от способа синхронизации, подразделяются на счетчики прямого счета (суммирующие) и на счетчики обратного счета (вычитающие). В интегральном исполнении выпускаются также реверсивные счетчики, в которых имеется специальный вход для переключения режима работы, т.е. направления счета. Многие типы счетчиков, выпускаемые промышленностью в интегральном исполнении, имеют дополнительные входы предустановки, позволяющие использовать эти счетчики в режиме регистра памяти.

В качестве разрядных триггеров счетчиков и делителей могут быть использованы двухступенчатые D-триггеры, Т- и JK-триггеры.

Ход работы

Счетчики относятся к последовательностным устройствам с циклически повторяющейся последовательностью состояний. Число, соответствующее количеству импульсов (поступивших на вход счетчика), при котором счетчик «возвращается» в исходное состояние, называется модулем или коэффициентом счета. Модуль счета, обычно, обозначают буквой М (или К_сч). Например, максимальный модуль счета счетчика из двух триггеров равен М = 2² = 4, трех триггеров - М = 2³ = 8 и т.д. В общем случае для n - разрядного счетчика - М = 2ⁿ. Модуль счета счетчика численно совпадает с модулем деления делителя частоты. Счетчик по модулю 8 позволяет реализовать (без дополнительных схемных затрат) делитель частоты на 8. Это значит, что данный делитель делит частоту входной импульсной последовательности на 8.

Асинхронный двоичный счетчик. Асинхронный двоичный счетчик представляет собой совокупность последовательно соединенных триггеров (D - или JK), каждый из которых ассоциируется с битом в двоичном представлении числа. Если в счетчике m триггеров, то число возможных состояний счетчика равно 2^m, и, следовательно, модуль счета М также равен 2^m. Счетная последовательность в двоичном суммирующем счетчике начинается с нуля и доходит до максимального числа 2^m - 1, после чего снова проходит через нуль и повторяется. В вычитающем двоичном счетчике последовательные двоичные числа перебираются в обратном порядке, и при повторении последовательности максимальное число следует за нулем.

Рассмотрим устройство двоичного суммирующего счетчика по модулю М=16, выполненного на базе JK-триггеров (рисунок. 1, а).

Как видно из рисунке. 1 (а), синхронизирующие входы всех триггеров, кроме крайнего левого (Т1), соединены с выходами предыдущих триггеров. Поэтому состояние триггера меняется в ответ на изменение состояния предыдущего триггера.

Из таблицы состояния счетчика (рис. 1, б) легко заметить, что значение разряда в выбранной позиции меняется тогда, когда в соседней справа позиции состояние переходит из «1» в «0», управление триггерами осуществляется задним фронтом синхроимпульсов (отрицательным перепадом напряжения импульса синхронизации).

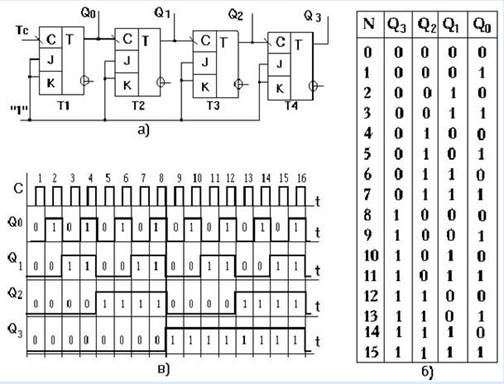
Рисунок. 1 - Схема а), таблица состояний триггеров б) и временные диаграммы, поясняющие работу в) последовательного четырехразрядного счетчика на JK - триггерах

Временные диаграммы, поясняющие работу асинхронного суммирующего счетчика приведены на рис. 1, в.

Счетчики обратного счета (вычитающие счетчики). На рис. 2 приведена схема асинхронного трехразрядного двоичного вычитающего счетчика, построенного на базе D-триггеров. Отметим, что условия для изменения состояний триггеров вычитающих счетчиков аналогичны условиям для суммирующих счетчиков с той лишь разницей, что они должны «опираться» на значения инверсных, а не прямых выходов триггеров. Следовательно, рассмотренный выше счетчик можно превратить в вычитающий, просто переключив входы «С» триггеров с выходов на выходы . Когда в качестве разрядных триггеров используются D-триггеры, синхронизируемые передним фронтом синхроимпульсов, для получения вычитающего счетчика (асинхронного) входы «С» последующих триггеров соединяются с прямыми выходами предыдущих, также как в счетчике прямого счета, построенного на JK-триггерах.

Работа вычитающего счетчика на D-триггерах наглядно иллюстрирована на рис. 2, (б). Из рис. 2 следует, что после нулевого состояния всех триггеров, с приходом первого синхроимпульса они устанавливаются в состояние «1». Поступление второго синхроимпульса приводит к уменьшению этого числа на одну единицу и т.д. После поступления восьмого импульса, снова, все триггеры обнуляются, и цикл счета повторяется, что соответствует модулю М=8.

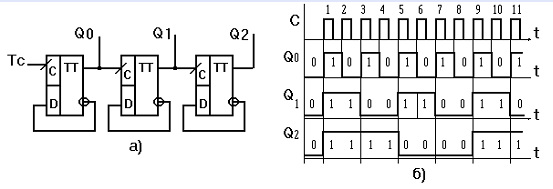
Рисунок 2  -  Схема временные диаграммы вычитающего трехразрядного счетчика на D - триггерах

В некоторых случаях необходимо, чтобы счетчик мог работать как в прямом, так и в обратном направлении счета. Такие счетчики называются реверсивными. Реверсивные счетчики могут быть как асинхронного, так и синхронного типа. Они строятся путем применения логических коммутаторов (мультиплексоров) в цепях связи между триггерами. Так, например, асинхронный реверсивный двоичный счетчик можно построить, если обеспечить подачу сигналов с прямого (при суммировании) или с инверсного (при вычитании) выхода предыдущего JK- или Т-триггера на счетный вход последующего. В случае, когда реверсивный счетчик строится на базе D-триггеров, управляемых передним фронтом, для получения режима прямого счета следует соединить инверсный выход предыдущего со счетным входом последующего триггера.

Все рассмотренные типы счетчиков могут быть использованы в цифровых устройствах «умеренного» быстродействия, когда частота следования синхроимпульсов не превышает критического значения, при котором время задержки установки триггеров последних (старших) разрядов счетчика становится соизмеримым с длительностью периода входных тактовых импульсов. В связи с этим, асинхронные счетчики строятся на относительно небольшое количество разрядов, так как при большем количестве разрядов выходные сигналы триггеров старших разрядов появляются позднее, чем управляющие фронты синхроимпульсов (поступающих на вход первого триггера).

Параллельные счетчики (синхронные счетчики). Как было уже сказано выше, параллельные счетчики бывают двух типов: синхронные параллельные и синхронные последовательные.

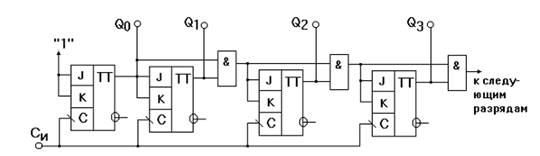
Рисунок 3 - Синхронный последовательный суммирующий счетчик на JK – триггерах

Синхронный последовательный счетчик. По способу подачи синхроимпульсов такие счетчики параллельные, т.е. синхроимпульсы поступают на все триггеры счетчика параллельно, а по способу управления (подачи управляющих импульсов) - последовательные. Схема синхронного последовательного счетчика, реализованного на JK-триггерах, приведена на рис. 3.

Синхронный последовательный счетчик обладает повышенным быстродействием, однако, за счет последовательного формирования управляющих уровней, на входы «J» и «К» счетных триггеров, быстродействие несколько уменьшается. От этого недостатка лишены параллельные синхронные счетчики, в которых формирование управляющих уровней и их подача на соответствующие входы триггеров счетчика осуществляется одновременно, т.е. параллельно. Пример реализации параллельного синхронного счетчика иллюстрирован на рис.  4.

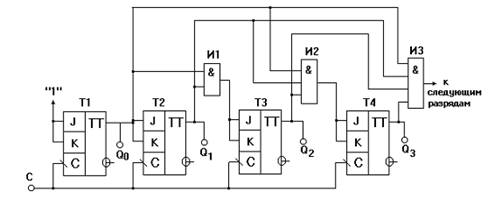
Рисунок 4 - Параллельный синхронный счетчик на JK - триггерах

Поскольку счетчик имеет одну общую линию синхронизации, состояние триггеров меняется синхронно, т.е. те триггеры, которые по синхроимпульсу должны изменить свое состояние, делают это одновременно, что существенно повышает быстродействие синхронных счетчиков.

Счетчики с произвольным коэффициентом счета. Принцип построения подобного класса счетных устройств состоит в исключении нескольких состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика.

Число избыточных состояний для любого счетчика определяется из следующего выражения:

М = 2^m - К_сч,                  (1)

где М - число запрещенных состояний, К_сч - требуемый коэффициент счета; 2^m - число устойчивых состояний двоичного счетчика.

Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа. Требуемое количество триггеров определяется из выражения

n= [log₂ К_сч],                  (2)

где [log₂ К_сч] - двоичный логарифм заданного коэффициента пересчета К_сч, округленный до ближайшего целого числа.

В каждом отдельном случае приходится применять какие-то конкретные методы получения требуемого коэффициента пересчета. Существует несколько методов получения счетчиков с заданным коэффициентом пересчета К_сч. Один их этих методов заключается в немедленном сбросе в «0» счетчика, установившегося в комбинацию, соответствующему числу К_сч. Его называют также методом автосброса. Рассмотрим пример реализации счетчика с К_сч=10 методом автосброса. Очевидно, что «сбрасывая» двоичный четырехразрядный счетчик на нуль каждый раз, когда он будет принимать состояние 1010, можно обеспечить «возврат» счетчика в исходное состояние после каждых десяти импульсов. Подобный прием удобно применять при использовании счетчиков в интегральном исполнении, имеющих ячейки конъюнкции (И) на входах установки в нуль, как это сделано в микросхеме К1533ИЕ5. В данном примере (Рис. 5) организованы соединения, обеспечивающие коэффициент пересчета К_сч =10.

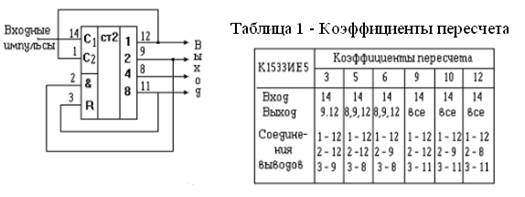
Рисунок 5 - Пример реализации счетчика с Kсч=10

Как следует из рис. 5, роль ячейки, выявляющей факт достижения кодовой комбинации 1010 на выходах счетчика, играет ячейка И, уже имеющаяся на входе сброса ИМС К1533ИЕ5.

В таблице 1 поясняются конфигурации соединений для получения различных коэффициентов пересчета с помощью счетчика К1533ИЕ5. Наиболее очевидные варианты получения коэффициентов (2, 4, 8, 16) в таблице не указаны. В графе «Соединения» таблицы указано, какие выводы микросхемы должны быть соединены между собой: например, указание 1-12 означает, что нужно соединить вывод 1 с выводом 12. В строках «Ввод» и «Выход» таблицы указаны номера выводов микросхемы, на которые следует подавать входные импульсы и с которых надлежит снимать выходные, соответственно. Следует отметить, что ИМС К1533ИЕ5 состоит из четырех счетных триггеров, один из которых имеет раздельные выводы входа и выхода, а остальные три триггера соединены последовательно по схеме асинхронного счетчика.

Синтез счетчика с произвольным коэффициентом счета. Один из методов проектирования счетчиков с заданным коэффициентом счета заключается в построении таблицы переходов, в первых столбцах которых будут отражены текущие состояния триггеров счетчика, а в последующих - следующие за ними состояния. Анализ таблицы позволяет установить те переходы, которые должны быть «сделаны» триггерами, входящими в состав счетчика. Затем с помощью управляющей таблицы соответствующего триггера находятся значения логических функций на управляющих входах триггеров, позволяющие осуществить эти переходы.

Рассмотрим пример синтеза синхронного двоично-десятичного счетчика на базе JK-триггеров. На рисунке 6 показан граф, поясняющий последовательность переходов десятичного счетчика, в таблице 2 - таблица переходов.

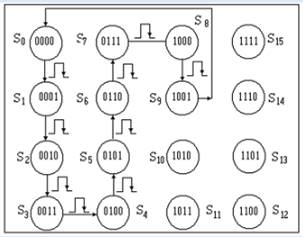
Рисунок 6 - Граф переходов двоично-десятичного счетчика

В правой части таблицы 2 приведены значения входных сигналов четырех триггеров. Для поиска этих значений должны быть проанализированы реализованные переходы, а затем с помощью управляющей таблицы определены соответствующие значения «J» и «K» входов триггеров.

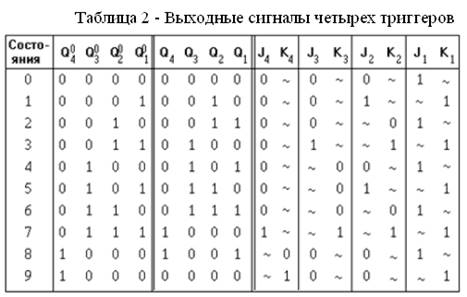
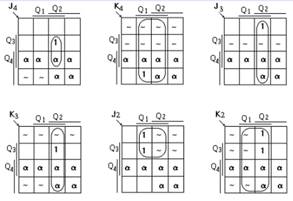
Рисунок 7 - Карты Карно для функции комбинационной логики двоично-десятичного счетчика

На рис. 7 приведены карты Карно для логических функций, которым должны соответствовать сигналы, присутствующие на управляющих входах триггеров (нулевые значения функций в клетки карты Карно не записаны).

После упрощения с помощью карт Карно полученные логические выражения, используемые для управления входами «J» и «К», выглядят

;     ;                        (3)

;       ;

;                   .

Просмотр столбцов J₁ и К₁ в таблице 2 показывает, что все значения либо «~», либо «1». Так как безразличные состояния могут также участвовать в процессе упрощения, то все клетки карты Карно для J₁ и К₁ оказываются заполненными символами «~», «1» и «a». Следовательно,

J₁ = K₁ = 1            (4)

На рис. 8 показана схема двоично-десятичного синхронного счетчика.

Если счетчик из-за какой-либо неисправности окажется в одном из запрещенных (неиспользуемых) состояний, то его работа может быть прервана специальным сигналом и также может быть подан сигнал тревоги о неисправности в схеме счетчика. Обнаружить это позволяет схема, реализующая выражение, описывающее функцию неиспользуемых состояний

f_н = Q₂ Q₄ + Q₃ Q₄.         (4)

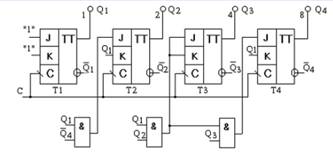
Рисунок 8 - Схема реализации двоично-десятичного синхронного счетчика

Задания к практической работе

Задание 1. Начертить УГО счетчиков и построить временные диаграммы их работы в режимах счета и записи информации. Построить таблицу режимов работы счетчиков по форме таблицы 3 и таблицы 4.

Задание 2. Исследовать работу счетчиков при одиночных импульсах по входу счета в различных режимах: сначала без, а затем с предварительной записью информации. Сделать выводы по результатам экспериментов.

Задание 3. Собрать схему последовательного 4-х разрядного двоичного счетчика:

­       Выходы соединить с любыми гнездами индикатора на вспомогательном устройстве; свечение светодиода свидетельствует о наличии на выходе сигнал лог.1.

­       Вход «R» соединить с блоком одиночных отрицательных импульсов (вход « » на вспомогательном устройстве).

­       Произвести сброс счетчика в нулевое состояние, для чего на вход R (уст.0) подать отрицательный импульс;

­       На вход «С» подать положительный импульсы; для исследования всех возможных состояний счетчика необходимо подать импульсов (где N- количество разрядов счетчика); все значения входных и выходных сигналов занести в таблицу переходов вида.

Таблица 3 - Режимы работы ИМС К155ИЕ9

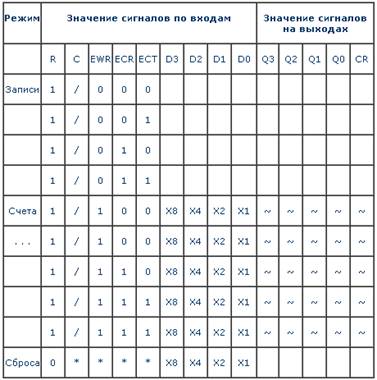
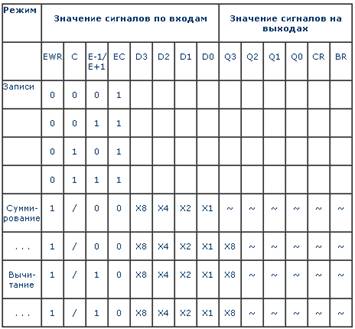
Таблица 4 - Режимы работы ИМС К155ИЕ13

Задание 4. Решите задачу. Каждое показание счётчика, фиксируемое в памяти компьютера, занимает 10 бит. Записано 100 показаний этого датчика. Каков информационный объём снятых значений в байтах?

Задание 5. Постройте счётчик для указанных модулей счёта:

а) К_сч=3;               б) К_сч=5;              в) К_сч=6;              г) К_сч=12.

Контрольные вопросы и задания

1.                 Чему равны K_сч. Восьмиразрядного двоичного и восьмиразрядного двоично-десятичного счетчиков?

2.                 Изобразите структурную схему и временные диаграммы работы трехразрядного двоичного вычитающего счетчика на основе T-триггеров с инверсным динамическим счетным входом.

3.                 В чем отличие схем и принципов функционирования счетчиков с параллельным и сквозным переносами?

4.                 В чем заключается принцип построения недвоичных счетчиков и как реализовать счетчик с К_сч.=8 на базе двоичных счетчиков?

5.                 Назовите основные типы и параметры счетчиков.

6.                 Составьте схему и постройте временные диаграммы работы последовательного трехразрядного двоичного счетчика. Объяснить его работу.

7.                 Составьте схему и постройте временные диаграммы работы параллельного трехразрядного двоичного счетчика.

8.                 Составьте схему и постройте временные диаграммы работы счетчика Джонсона. Объяснить его работу.

9.                 Составьте схему двоично-десятичного по заданной преподавателем таблице переходов.

10.            Составьте схему недвоичного счетчика с модулем пересчета М=5,6,7,11. Объяснить его работу.

11.            Составьте схему счетчика делителя с коэффициентом пересчета М=4,6,9,11.

12.